山區高墩大跨度連續剛構橋穩定性與參數影響分析

唐峰，李德建

(1.中交四公局第二工程有限公司,北京 101149；2.中南大學 土木工程學院，湖南 長沙 410075)

?

山區高墩大跨度連續剛構橋穩定性與參數影響分析

唐峰1，李德建2

(1.中交四公局第二工程有限公司,北京 101149；2.中南大學 土木工程學院，湖南 長沙 410075)

摘要:以山區某高速公路高墩大跨度連續剛構橋為工程實例，對其在最高墩階段、最大懸臂階段和成橋階段的線彈性穩定性進行計算，找出穩定安全系數最低的階段。在此基礎上，對其進行非線性穩定分析，討論非線性因素對穩定性的影響，探討相關參數如混凝土強度等級、橋墩縱向尺寸、雙肢薄壁橋墩間距、系梁設置、基礎剛度對穩定安全系數的影響，并得出結論，研究成果可為高墩大跨度連續剛構橋的設計與施工提供參考。

關鍵詞：高墩；大跨度；連續剛構橋；穩定性；施工階段；非線性

近年來，隨著高速公路建設不斷向山區延伸，我國高墩大跨度連續剛構橋得到很大發展，建造技術已達到世界領先水平，并進一步向薄壁、高墩、大跨方向發展，這使得穩定問題日益突出，若處理不當，橋梁結構可能會發生整體或局部失穩而使結構喪失承載力[1-4]。因此，有必要對高墩大跨度連續剛構橋的穩定性進行研究，以保證結構的安全。尤其是對高墩大跨度連續剛構橋各典型施工階段進行分析，找出穩定性最不利施工階段，并對其進行彈塑性穩定性分析，得出其真實的穩定安全系數，用以指導設計和施工，就顯得尤為重要。本文以布林大橋為工程背景分析高墩大跨度連續剛構橋的線彈性穩定以及非線性穩定，并對穩定的影響參數進行討論。布林大橋為貴州山區跨越山區峽谷的一座高墩大跨度連續剛構橋，跨徑布置為105 m+200 m+105 m，最高墩為1號墩，其墩高為127.6 m 。主墩墩身采用雙肢變截面矩形空心墩，肢間凈間距850 cm，縱向每肢外側均按200∶1放坡，橫向根據墩高采用分段放坡形式，從上到下分別采用80∶1和50∶1共2種坡率。空心墩壁厚90 cm，且壁厚沿墩高保持不變。橋梁總體布置見圖1，1號墩構造見圖2。

圖1　布林大橋橋型布置圖Fig.1 Layout drawing of Bulin Bridge

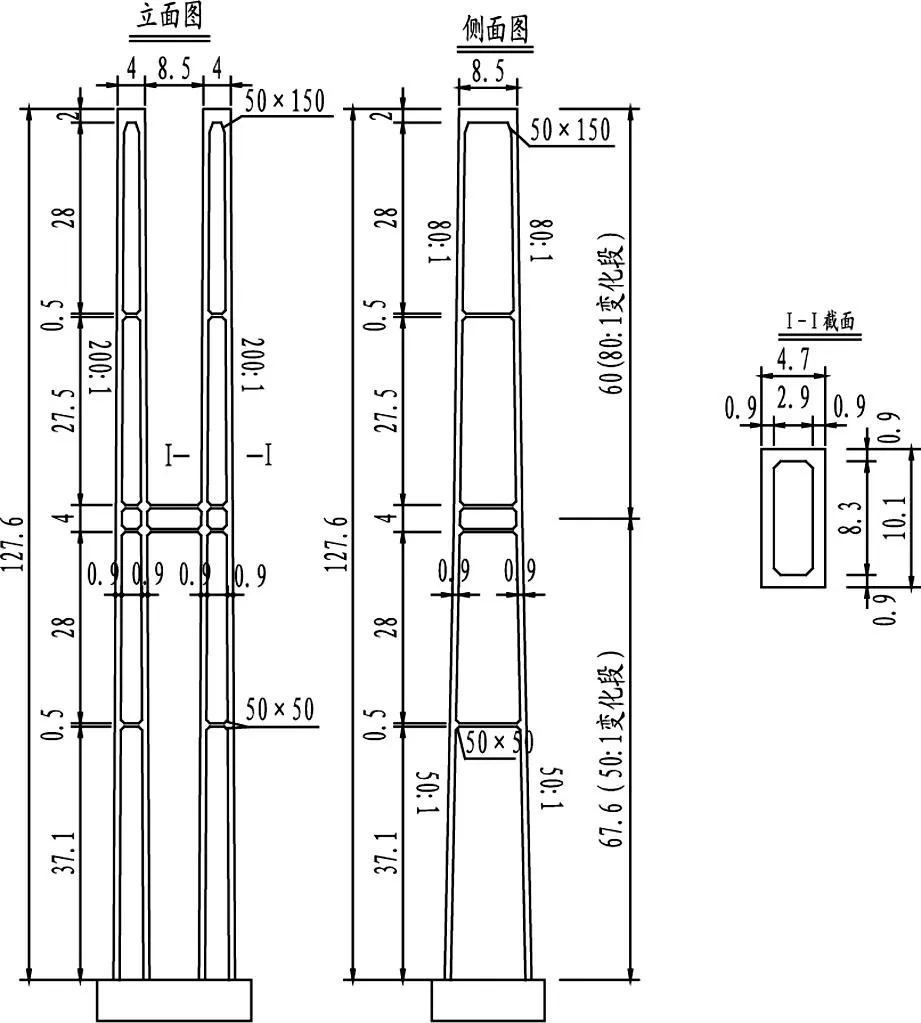
圖2　1號高墩構造圖Fig.2 Structure diagram of No.1 pier

1線彈性穩定分析

1.1有限元模型的建立

利用大型橋梁專業分析軟件Midas-civil的空間梁單元模型對布林大橋的3個典型階段的線彈性穩定進行分析，即最高墩的自體穩定性、最大懸臂階段的穩定性和成橋階段的穩定性。

布林大橋的主墩采用C55混凝土，主梁采用C60混凝土。模型中的邊界條件按如下處理：

最高墩階段：墩底與承臺固結，墩頂自由。

最大懸臂施工階段：墩底與承臺固結，墩頂與箱梁底固結，最大懸臂兩端自由。

成橋階段：主墩墩底與承臺固結，墩頂與箱梁底固結，邊跨梁端約束為鉸結，即約束其豎向、橫向的線自由度和橫向轉角自由度，釋放其他方向的自由度。

計算分析時考慮恒載(一期恒載以及二期恒載)、活載、施工荷載和縱橋向以及橫橋向的靜風荷載的組合。

1.2最高墩階段的線彈性穩定計算

對布林大橋127.6 m高墩達到最大墩高時的線彈性穩定問題進行分析，考慮以下3種工況。

工況1：自重；

工況2：自重+橫向風荷載；

工況3：自重+順橋向風荷載。

通過Midas-civil的線彈性屈曲分析，得到布林大橋達到最高墩階段的線彈性穩定安全系數和對應的屈曲模態如表1所示。

表1最高墩階段的線彈性穩定安全系數及對應的屈曲模態

Table 1 Linear elastic stability safety coefficient and buckling mode at the stage of completion of pier construction

計算工況安全系數λ對應的屈曲模態工況122.53縱向屈曲工況222.53縱向屈曲工況322.52縱向屈曲

從表1可以看出，3種工況的第1類線彈性穩定安全系數都大于4，根據受壓柱結構彈性穩定安全系數的規定[5]，該階段的穩定性滿足規范要求，在各種工況下的屈曲模態都表現為縱向屈曲。

1.3最大懸臂階段的線彈性穩定計算

計算荷載：1)橋墩自重；2)由于澆筑誤差，引起一側主梁自重增加4%，另一側減少4%；3)掛藍、施工機具和現澆塊件的動力效應，一端取1.2，另一端取0.8，掛藍自重取800 kN;4)掛藍一側跌落，取動力放大系數為2；5)施工材料堆放荷載，取一懸臂承受8.5 kN/m的豎向均布荷載，并在其端頭作用200 kN的豎向集中力，另一懸臂空載；6)橫橋向風荷載；7)順橋向風荷載。

當掛藍正常工作時，計算以下3種工況的穩定性。

工況1：1)+2)+3)+5)

工況2：1)+2)+3)+5)+6)

工況3：1)+2)+3)+5)+5)

當掛藍跌落時，計算以下3種工況的穩定性。

工況4：1)+2)+4)+5)

工況5：1)+2)+4)+5)+6)

工況6：1)+2)+4)+5)+7)

計算結果如表2所示。

表2最大懸臂階段線彈性穩定安全系數及對應的屈曲模態

Table 2 Linear elastic stability safety coefficient and buckling mode at the stage of the largest cantilever

計算工況安全系數λ對應的屈曲模態工況116.552橋墩縱向屈曲工況216.540橋墩縱向屈曲工況316.547橋墩縱向屈曲工況416.539橋墩縱向屈曲工況516.527橋墩縱向屈曲工況616.533橋墩縱向屈曲

從以上結算結果可以看出，最大懸臂階段的穩定安全系數較最高墩階段降低了27%左右，但穩定安全系數仍然遠大于4。

1.4成橋階段的線彈性穩定計算

成橋階段的穩定分析考慮的荷載有：自重、二期恒載和汽車活載。

計算以下2種工況。

工況1：自重+二期恒載

工況2：自重+二期恒載+全橋滿布汽車活載

計算結果如表3所示。

表3成橋階段線彈性穩定安全系數及對應的屈曲模態

Table 3 Linear elastic stability safety coefficient and buckling mode at the stage of completion of the whole bridge

計算工況安全系數λ對應的屈曲模態工況118.02橋墩縱向屈曲,主梁豎向彎曲工況217.50橋墩縱向屈曲,主梁豎向彎曲

從表3可知，全橋合龍完成后，結構的約束增強，成橋階段的穩定安全系數均較最大懸臂階段大，該階段也具有足夠的穩定安全系數。

從以上3個典型階段的線彈性穩定分析可知，最大懸臂階段在工況5荷載作用下的穩定安全系數最小，故以下的非線性穩定分析及穩定性影響參數分析均是以此工況下最大懸臂階段為討論分析的。

2非線性穩定分析

結構的線彈性穩定計算是基于結構的剛度較大，荷載引起的位移較小且結構的本構模型為線彈性模型這樣一個假定進行的。但是對于高墩大跨連續剛構橋，其薄壁空心墩的剛度較小，在重力、施工荷載、風荷載及初始缺陷的作用下，墩頂可能會發生較大的偏位，部分材料可能已經進入彈塑性狀態或已達到極限強度，這時結構的穩定性分析應考慮幾何非線性和材料非線性的影響。

2.1零缺陷作用下幾何非線性穩定計算

假定材料為線彈性，利用Midas-civil建立空間梁單元，對最大懸臂階段的幾何非線性穩定進行計算，計算結果如表4所示。

表4　幾何非線性穩定安全系數

從以上計算結果可以看出，計入幾何非線性后，穩定安全系數的變化幅度在10%以內，這說明結構的剛度較大，幾何非線性對穩定的影響不大，這主要是由于假設的材料為彈性所引起的。

2.2初始缺陷作用下幾何非線性穩定計算

對于高墩而言，混凝土澆筑的實際位置與理論位置難免存在一定的誤差，而在日照溫差的影響下，高墩也會發生一定的變形，因此，考慮這些因素的影響，高墩的初始缺陷是必然存在的。特征矢量屈曲模態可以認為是最接近于實際屈曲模態的預測值，因此本文采用以特征向量為依據的方法給結構施加初始缺陷[6]。本文考慮最大初始缺陷分別為0.1，0.3和0.5 m進行幾何非線性穩定計算。計算結果如表5所示。

表5初始缺陷對幾何非線性穩定的影響

Table 5 Influence of initial defects on geometrical nonlinear stability

初始缺陷大小/m00.10.30.5穩定安全系數15.1315.0214.8114.62穩定安全系數變化量/%0-0.70-2.10-3.40

從以上計算結果可以看出，考慮初始缺陷后，幾何非線性穩定安全系數都發生不同程度的降低，但降低幅度不大，幾何非線性的穩定安全系數仍較大，這座橋具有足夠的幾何非線性穩定安全系數。

2.3雙重非線性穩定分析

本文的混凝土非線性本構關系采用國內外廣泛采用的Hognestad公式，其具體表達式為：

(1)

圖3　C55混凝土的本構關系Fig.3 Constitutive relation of C55 concrete

考慮雙重非線性，利用Midas-FEA的空間實體單元對布林大橋在最大懸臂階段的穩定性進行計算，迭代的方法采用收斂性較好的修正的牛頓拉普森法，以位移收斂標準進行計算。由于第1類穩定特征值屈曲荷載是結構第2類穩定臨界荷載的上限[7]，可以作為雙重非線性穩定分析的給定荷載，因此本節計算荷載取1.3節工況5的20倍。布林大橋在計算發散前的最大荷載加載系數為0.15，所以考慮雙重非線性后，布林大橋的穩定安全系數為0.15×20=3。可見，考慮雙重非線性后的穩定安全系數大于2.5，根據受壓柱結構彈塑性穩定安全系數的規定[5]，滿足規范要求。

從以上計算結果可以看出，布林大橋考慮材料非線性后，結構的穩定安全系數發生大幅度的下降，為考慮幾何非線性結果的19.8%，為線彈性穩定安全系數的18.2%。因此，為得到結構真實的極限承載力，應考慮雙重非線性，對第二類穩定問題進行計算分析。

3穩定性的影響參數分析

3.1混凝土強度等級對穩定性的影響

布林大橋高墩采用的是C55的混凝土，考慮C40，C50和C60不同標號的混凝土進行分析，討論混凝土強度等級對穩定性的影響。計算結果如表6所示。

表6混凝土強度等級對穩定性的影響

Table 6 Influence of different strength grades of concrete on stability

混凝土強度等級C40C50C55C60第1類穩定安全系數15.1416.0716.5316.76穩定安全系數變化量/%-8.40-2.8001.40

從表6的計算結果可以看出，隨著混凝土的強度等級的提高，穩定系數增大，但隨著混凝土標號的增大，穩定安全系數的增幅趨緩，從C55變化到C60，穩定系數僅增大了1.4%，且高標號的混凝土還會帶來現場澆注麻煩，結構的脆性增大等問題。因此，對高墩來說，從穩定性角度出發，當混凝土標號達到C50以上后，追求更高標號的混凝土是沒有必要的。

3.2橋墩縱向尺寸對穩定性的影響

布林大橋最高墩縱向尺寸變坡率從墩頂到墩底采用200∶1，現采用不同的縱向變坡率討論縱向尺寸對穩定性的影響，增加180∶1和250∶1共2種變坡率進行討論分析,墩底的縱向尺寸從原來的5.276 m變為5.418 m和5.021 m。計算結果如表7所示。

表7　橋墩縱向尺寸對穩定性的影響

從表7可以看出，隨著縱向尺寸的增大，橋墩的穩定系數也增大，縱向尺寸在原設計尺寸0.5 m左右范圍內變化，其對穩定系數的影響也較有限，穩定系數的變化值在10%以內。

3.3雙肢薄壁橋墩間距對穩定性的影響

連續剛構雙肢薄壁墩間距的設計通常是從使得橋墩能夠抵抗施工過程中可能出現的最大不平衡彎矩來考慮的[8]。為討論雙肢薄壁墩的間距設置在滿足抗彎剛度要求的前提下對穩定性的影響，采取幾種不同的橋墩間距進行穩定計算。布林大橋雙肢薄壁墩的中心間距為12.5 m，現增加10.5，11.5和13.5 m這3種間距進行討論計算。計算結果如表8所示。

表8雙肢薄壁橋墩間距對穩定性的影響

Table 8 Influence of distance between two thin-walled piers on stability

雙肢薄壁橋墩間距/m10.511.512.513.5第1類穩定安全系數16.0716.3016.5316.55穩定安全系數變化量/%-2.80-1.3000.10

從表8的計算結果可以看出，隨著雙肢薄壁墩間距的增大，穩定系數也增大。但各種間距下，穩定安全系數相差不大，因此，從穩定性及經濟性角度考慮，雙肢薄壁墩的間距在滿足抗彎剛度要求的前提下，不宜取得過大。

3.4系梁設置對穩定性的影響

為分析系梁設置對穩定性的影響，設置不同的系梁個數對穩定性進行計算。

布林大橋的系梁的設置情況分為以下4種。

情況1)：未設置系梁；

情況2)：在距墩頂30 m的空心墩橫隔板處設置1道系梁；

情況3)：在距墩頂58和62 m的空心墩橫隔板處各設置1道系梁(布林大橋的實際情況)；

情況4)：在距墩頂30，58和62 m的空心墩橫隔板處各設置1道系梁。

計算結果如表9所示。

表9　系梁設置對穩定性的影響

從表9計算結果可以看出，通過設置系梁都可以提高其穩定安全系數。在墩的中間設置1道系梁，對穩定安全系數的提高較大；但另一情況，即在靠近墩頂的地方設置1道系梁，其對穩定性影響較小，這說明系梁設置的位置，對穩定性有較大影響。與在墩的中間設置1道系梁相比，設置2道系梁并沒有顯著提高高墩的穩定安全系數，這說明當高墩的縱向剛度大到一定程度之后，設置更多的系梁是沒有必要的。

3.5基礎剛度對穩定性的影響

前面的計算都假定基礎的剛度很大，忽略基礎變形對穩定的影響，將墩底節點直接固結。為討論基礎剛度對穩定性的影響，下面對考慮樁-土作用的最大懸臂階段的穩定性進行計算分析。本文采用分層文克爾彈簧模型[9-11]，將樁基礎進行有限元離散，在單元節點上建立彈簧支撐，模擬樁周土對樁單元的約束。彈簧的剛度按《公路橋涵地基與基礎設計規范》(JTG D63—2007)上的m法進行計算。

布林大橋最大懸臂階段考慮樁土作用的有限元模型如圖4所示。樁頂節點與承臺底節點剛性連接，樁底節點固結，在樁的其他節點加上相應的水平彈簧約束。

圖4　考慮基礎剛度的有限元模型Fig.4 Finite element model considering foundation stiffness

計算結果如表10所示。

表10　基礎剛度對穩定性的影響

從表10的計算結果可以看出，基礎剛度對穩定安全系數也有一定程度的影響，計入基礎剛度后，線彈性穩定安全系數降低了12%。當進行初步設計時，可以不考慮基礎剛度的影響，采用墩底固結的方式進行計算，快速得到初步的結果。而進行施工圖設計時，應計入基礎變形對結構的影響，精確計算連續剛構橋的內力和穩定性。

4結論

1)通過對布林大橋在最高墩階段、最大懸臂階段和成橋階段的第1類線彈性穩定分析可知，最大懸臂階段的穩定安全系數最小，應對其作重點分析。

2)與線彈性穩定相比，考慮幾何非線性后，結構的穩定安全系數變化不大，說明橋的剛度較大，幾何非線性對其穩定影響較小。同時，初始缺陷對橋梁的幾何非線性穩定的影響也較小。

3)考慮材料非線性之后，結構的穩定安全系數發生了大幅度的降低。因此，為得到結構真實的極限承載力，僅進行結構的線彈性屈曲分析或幾何非線性穩定分析是不夠的，應進行雙重非線性分析。

4)混凝土強度等級、橋墩的縱向尺寸、雙肢薄壁墩的間距、系梁設置的個數及位置、基礎剛度等對穩定性都有一定的影響。通過對結構穩定的影響因素進行分析探討，得出了一些有益結論，可對高墩大跨連續剛構橋的設計和施工提供參考。

參考文獻：

[1] 馬保林.高墩大跨連續剛構橋[M].北京：人民交通出版社,2001.

MA Baolin. Long-span continuous rigid-frame bridge with high piers[M].Beijing:China Communication Press,2001.

[2] 陳驥.鋼結構穩定理論與設計[M].北京：科學出版社,2011.

CHEN Ji.The theory and design of the structure stability of the steel[M].Beijing:Science Press, 2011.

[3] 郭梅.高墩大跨連續剛構橋穩定性分析[J].西安公路交通大學學報,1999,19(3):31-35.

GUO Mei. Stability analysis of long-span continuous rigid-frame bridge with high piers[J]. Journal of Xi’an Highway Communication University,1999, 19(3):31-35.

[4] 陳懷勇，湯兆新，陳勝利.高墩連續剛構橋穩定性分析[J].交通標準化，2010(6)：83-84.

CHEN Huaiyon, TANG Zhaoxin, CHEN Shengli. Stability analysis of high pier continuous rigid frame bridge[J].Communications Standardization, 2010(6)：83-84.

[5] JTG/T D65-01—2007,公路斜拉橋設計細則[S].

JTG/T D65-01—2007, Design specification for highway cable stayed bridge[S].

[6] 賴煉，白光耀.大跨度鋼管砼拱橋考慮初始幾何缺陷對極限承載力影響的計算機模擬[J].廣西大學學報(自然科學版)，2006，31(增)：323-326.

LAI Lian, BAI Guangyao.The whole computer simulation process for initial geometry defects affect ultimate bearing capacity of concrete-filled steel tubular arch bridges[J]. Journal of Guangxi University(Natural Science Edition),2006，31(Suppl)：323-326.

[7] 黃海彬.高墩大跨連續剛構橋靜力極限承載力及抗風性能研究[D].長沙：中南大學，2011.

HUANG Haibin. Research on static ultimate bearing capacity and wind-resistance performance of long-span continuous rigid-frame bridges with high piers[D].Changsha:Central South University,2011.

[8] 徐君蘭，顧安邦.連續剛構橋主墩剛度合理性的探討[J].公路交通科技，2005,22(2)：59-62.

XU Junlan, GU Anbang. Discussion of rationality of rigidity of continuous rigid-frame bridge[J]. Journal of Highway and Transportation Research and Development, 2005,22(2)：59-62.

[9] 劉釗，譚皓，文武松，等.連續剛構橋的群樁基礎計算模型研究[J].橋梁建設，2005(5)：1-4.

LIU Zhao,TAN Hao,WEN Wusong.Research of calculation models for group pile foundation of continuous rigid-frame bridge[J].Bridge Construction, 2005(5)：1-4.

[10] 諶啟發.虎跳門大橋樁基等效模擬計算[J].橋梁建設，2000(1)：69-71.

CHEN Qifa. Equivalent analog calculation for pile foundation of hutiaomen prestressed concrete continuous rigid-frame bridge[J].Bridge Construction, 2000(1)：69-71.

[11] 彭富強，李德建. 基于柔度系數求解橋梁樁基對橋墩約束剛度的有限元數值分析[J].鐵道科學與工程學報，2012，9(2)：62-65.

PENG Fuqiang, LI Dejian. FEM numerical analysis of elastic bearing rigidity of pile foundation based on inverse deduction of flexibility coefficient [J]. Jounal of Railway Science and Engineering, 2012,9(2)：62-65.

(編輯陽麗霞)

Stability of long-span continuous rigid-frame bridge withhigh piers in mountain areas in different construction stage andrelevant parameter influence analysis

TANG Feng1，LI Dejian2

(1. Second Engineering Co.Ltd of CCCC Fourth Highway Engineering Co.Ltd, Beijing 101149,China;2.School of Civil Engineering, Central South University, Changsha 410075,China)

Abstract:On the background of a long-span continuous rigid-frame highway bridge with high piers in mountain areas, linear elastic stabilities were analyzed at the stages of completion of pier construction,the largest cantilever and completion of the whole bridge for finding the minimum stability safety coefficient , respectively. On this basis, nonlinear stability of the bridge was analyzed and the influences of nonlinear factors on stability were discussed. The influences of different parameters such as the concrete strength grade, longitudinal dimension of the pier, distance between the twin thin-walled piers, tie beam installation and foundation rigidity on stability were explored, and then some useful conclusions were drawn. The results can provide some references for the design and construction of long-span continuous rigid-frame bridge with high piers.

Key words:high pier; long-span; continuous rigid-frame bridge; stability; construction stage; nonlinearity

中圖分類號：U443.22

文獻標志碼：A

文章編號：1672-7029(2016)03-0506-06

通訊作者：唐峰(1979-)，男，湖南邵陽人，高級工程師，從事橋梁工程施工與管理工作；E-mail：p30560632@qq.com

基金項目：湖南省交通科技計劃項目(201022)

收稿日期：2015-10-28