巷道調熱圈半徑及其溫度場分布的數值模擬研究

何發龍,魏亞興,胡漢華,王娟

(1.天津城建大學 能源與安全工程學院，天津 300384;2.中南大學 資源與安全工程學院，湖南 長沙 410083；3.中匯國際保險經紀股份有限公司，北京 100022)

?

巷道調熱圈半徑及其溫度場分布的數值模擬研究

何發龍1,2,魏亞興2,胡漢華2,王娟3

(1.天津城建大學 能源與安全工程學院，天津 300384;2.中南大學 資源與安全工程學院，湖南 長沙 410083；3.中匯國際保險經紀股份有限公司，北京 100022)

摘要:為探究巷道圍巖傳熱過程中調熱圈溫度場的分布，建立25組數值試驗模型模擬調熱圈傳熱過程，并選定原巖溫度、調熱圈半徑、熱導率為影響因素，以巷道壁面溫度為目標因子，進行正交試驗分析，得出各因素對壁面溫度的影響大小依次為原巖溫度>熱導率>調熱圈半徑。運用統計分析，擬合出壁面溫度熱力學計算式，其相關系數達到0.996。同時，在前期研究基礎上，探討巷道通風時間因素和調熱圈半徑之間聯系，得到調熱圈半徑與通風時間的擬合計算式。將2個計算式聯立可以作為巷道壁面溫度表征公式，用于預測巷道壁面溫度。

關鍵詞：數值模擬；圍巖傳熱；調熱圈；壁面溫度；正交試驗；線性回歸

礦井通風是保證礦山開采的重要組成部分，巷道掘進初期，風流會帶走巷道壁面處圍巖熱量而使得原巖的熱平衡被打破。隨著通風的繼續，深處將不斷進行原巖熱流的補充，直至達到新的平衡。平衡后的圍巖溫度場就是調熱圈溫度場，未受通風溫度影響的邊界，即原始巖溫等溫線所包圍的范圍就是巷道圍巖調熱圈[1～3]。研究調熱圈溫度場，并探討壁面溫度、調熱圈半徑等熱力學關系，這對保證礦山安全生產及井下熱環境控制具有重要意義。

1數值模擬試驗設計

1.1模型的建立與邊界條件

實際通風過程中，不同采深處巷道壁面溫度是變化的，這為實際熱交換分析和風溫預測帶來難度。井下熱環境是一個復雜、動態的過程，整個調熱圈趨向穩定需要經過很長時間，且情況各不相同。但是當通風足夠時間后，即調熱圈溫度場達到穩定后，風流對圍巖溫度場的影響可忽略不計[3]。采用微元思想，將一條長巷道細分為很多小段，便于建立數值模型。基于此，建立小段長度的巷道模型來模擬分析調熱圈溫度場，采用正交試驗方法，分析各因素對巷道壁溫的影響，并根據試驗結果擬合壁溫計算式。

正交模擬試驗中巷道長度全部設置2 m，假設巷道經過長時間傳熱，調熱圈溫度場已基本穩定，忽略巷道內風流對該段巷道調熱圈溫度場的影響。模擬計算過程中，給定巷道內風溫25 ℃，在不考慮風流影響情況下設置風速為0。空間坐標系下Z=0處為速度進口，Z=2處為自由流出口，巷道壁面設置為圍巖固體域與巷道內氣體域的耦合接觸面，將壁面溫度作為正交試驗目標因子進行分析[4-8]。圖1為正交1號實驗的斷面模型及其網格劃分圖，其余各次試驗模型圖類似，此處省略。

1.2正交試驗

正交試驗設計是在試驗前借助于一種現成的正交表，科學地挑選實驗條件，找出主次關系并確定搭配方案或最優化工藝條件[9-12]。因此，分析研究的礦井巷道模型基于長時間通風后，調熱圈已穩定后的情況。根據調熱圈理論及傳熱學知識可知，微元后的調熱圈溫度場與該水平調熱圈外原巖溫度(ty)、圍巖的熱導率(λ)以及調熱圈半徑(Rt)是相關的。調熱圈外原巖溫度(ty)可由相關地溫計算公式確定；調熱圈半徑(Rt)也因地質條件不同而不同，調熱圈半徑一般為15～50 m；熱導率(λ)則取決于巖石的巖性。據此，分別給定各因素的水平值，見表1。表2為L25(53)正交試驗設計及其結果。

圖1　1號試驗模型Fig.1 No.1 numerical experiment model

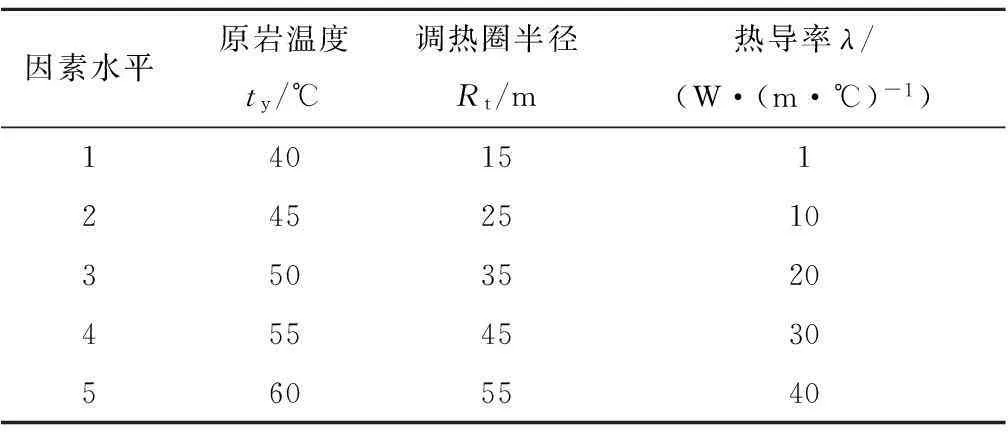
因素水平原巖溫度ty/℃調熱圈半徑Rt/m熱導率λ/(W·(m·℃)-1)1401512452510350352045545305605540

2模擬試驗結果分析

如表2所示，經過25次正交模擬試驗后可以分別得到巷道壁面的平均溫度值及其調熱圈溫度場，圖2和圖3分別為1號正交試驗的調熱圈溫度場彩云圖及其調熱圈溫度等值線圖，以此來說明調熱圈的溫度分布情況，其余各次實驗情況類似，此處省略。

綜合圖2和圖3可知，調熱圈內溫度自深部圍巖向巷道壁面逐漸降低，在靠近巷道處溫度梯度變化較大，等值線分布較為密集。在經過長時間通風后的穩定調熱圈溫度場內，其溫度等值線基本成一組半徑不同的同心圓，溫度沿半徑方向逐漸增大，深處圍巖溫度變化梯度小于巷道周邊附近。根據正交試驗數據，分別以Rt，ty和λ的5個水平值為橫坐標，以其計算結果的溫度極差平均值為縱坐標繪制其極差分布圖，見圖4。

表2　正交試驗及其結果表

結合表2的正交試驗結果與圖4可以看出，原巖溫度因子的極差值最大，說明其對巷道壁面溫度影響最明顯；調熱圈半徑的極差值最小，其對壁面溫度影響最小；熱導率因子的極差值處于中間水平，但是也遠遠高于調熱圈半徑因子的影響。

將圖4中半徑、原巖溫度以及熱導率的極差分布情況分別進行公式擬合，以便直觀了解各因素對壁面溫度的作用，見表3。

圖2　1號實驗溫度場彩云圖Fig.2 Temperature field contour of No.1 model

圖3　1號實驗溫度場等值線圖Fig.3 Temperature field contour line of No.1 model

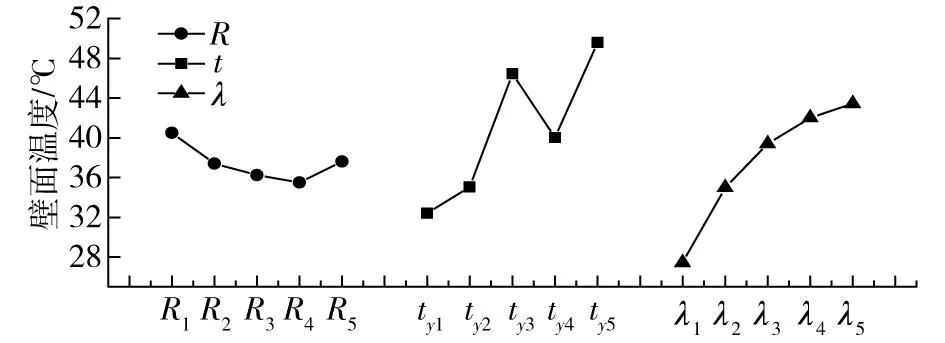
圖4　壁面溫度正交試驗極差分布圖Fig.4 Orthogonal test range graph of wall temperature

類別擬合公式R2公式編號半徑Tb=0.7753R2-5.4164R+45.1750.9785(1)原巖溫度Tb=0.6057ty3-5.7355ty2+19.938ty+16.7220.7558(2)熱導率Tb=27.989λ0.29050.9846(3)

3壁面溫度的預測

各單因素關于極差分布的簡單單因素擬合公式見表3，這些經驗擬合公式可以直觀說明各因素對調熱圈內溫度場的影響，并為正交試驗數據公式擬合提供信息。根據25次正交試驗數據，借助SPSS數據分析軟件得到壁面溫度關于調熱圈半徑、原巖溫度以及熱導率的擬合公式，公式相關系數達到0.969，見公式(4)，圖5為模型預測值與試驗值的對比圖。

圖5　預測溫度與模擬溫度值比較圖Fig.5 Contrast figure of prediction temperature and simulation temperature

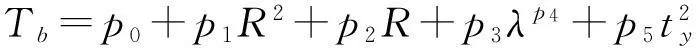
(4)

其中：p0=77.568 3，p1=0.003 4，p2=-0.274 0，p3=6.095 1，p4=0.290 5，p5=0.003 9，p6=-1.595 7，p7=0.006 1，p8=0.004 4，p9=-0.005 2。

式中：Tb為壁面溫度，℃；R為半徑，m；ty為原巖溫度，℃；λ為熱導率, W/(m·℃)。

公式(4)作為壁面溫度的表征公式，其復相關系數達到0.996，sig.值為0.000，擬合方程高度顯著，對于壁溫預測提供一定依據。方程中顯示，調熱圈半徑、原巖溫度以及熱導率三因素之間還存在兩兩交互作用，其對壁溫目標因子的作用不是簡單的一次關系。

4調熱圈半徑分析

井巷調熱圈半徑一般在通風3 a之后趨于穩定，但是在某一巷道掘進初期，其調熱圈半徑是與通風時間相關。當巷道剛開始掘進時，其調熱圈半徑較小，隨著通風時間的繼續增加，在通風時間增加到某一定值時，圍巖受風流冷卻速度與徑向深處圍巖的傳熱速度相當時，可認為圍巖與風流已經充分完成熱交換，調熱圈半徑達到峰值并保持不變。

需要指出的是，公式(4)中的調熱圈半徑是建立在風流與圍巖的熱交換穩定后的基礎上，即在經過通風時間τ時，圍巖傳熱的調熱圈已經穩定，其半徑確定為τw，不再隨時間的增加而增加。國內外很多學者對于R和τ之間的關系都有研究，也給出了其相關計算式，但是τ的取值范圍應為(0，τw)。由于τ取值范圍的影響，以往學者描述的R和τ之間的關系具有局限性。為此，考慮將τ取值范圍擴大，在文獻[2]所提供的數據基礎上，繪制該條巷道的R和τ曲線關系圖，并擬合出其經驗公式。

文獻[2]指出，康家灣礦一號斜井-294 m巷道不同通風時期的情況(假設其通風年限為5，10，25，60，180，300，360，450，600和900 d，穩定后)，各時期的調熱圈半徑見表4。

由表4可以得出，當通風時間達到900 d后，其調熱圈半徑基本保持不變，在通風還未達到穩定時，調熱圈半徑隨著通風時間的增加而增加。對上述數據進行分析，繪制R和τ之間的曲線關系圖，并運用統計學知識進行數據擬合，得到其關系式，見公式(5)，模型相關性系數為0.991 8。將原始數據與式(5)模型計算數據進行匯總對比，見圖6。

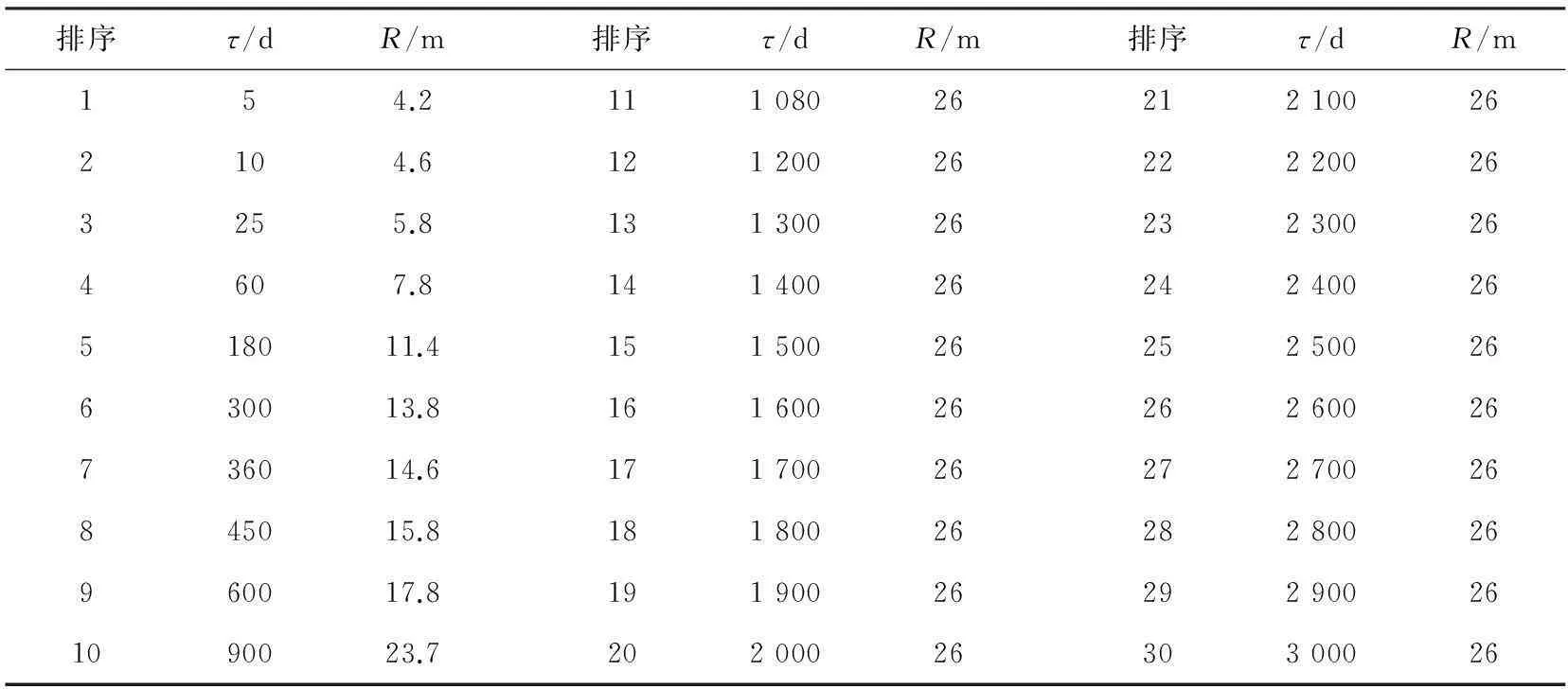
表4　不同通風時間下調熱圈半徑關系

圖6　R和τ曲線擬合對比Fig.6 Contrast graphof R and τ fitting line

(5)

其中，p1=-28.857 809 385 962 7，p2=701.480 214 735 005，p3=33.435 871 669 943 9，p4=11 631.291 283 005 4。

式中：R為調熱圈半徑，m；τ為通風時間，d。

可知，式(5)的相關系數較高，顯著性水平較高，其對R和τ之間的曲線擬合度較高，能夠說明其二者之間的關系。調熱圈起著緩沖作用，它使巖體內部具有的巨大熱量緩慢的向外分散，常用調熱圈半徑(從巷道軸心至外邊界的距離)和調熱圈溫度場(調熱圈內的溫度分布)來表征圍巖的熱移動。

5結論

1)建立圍巖傳熱調熱圈溫度場數值模型，通過正交試驗設計得出，對壁溫影響大小依次為原巖溫度、熱導率、調熱圈半徑。

2)以壁面溫度為表征因子，根據正交試驗數據得到了壁面溫度的表征計算式，相關系數高于0.95，預測值與試驗值誤差較小，可用于巷道壁面溫度預測。

3)在上述研究基礎上，分析圍巖調熱圈半徑與通風時間的關聯，建立調熱圈半徑與通風時間的擬合計算式，方程擬合程度較好。

參考文獻：

[1] 楊高飛. 礦井圍巖與風流熱濕交換規律的實驗與模擬研究[D]. 天津:天津大學, 2008.

YANG Gaofei.Experimental research and simulation on heat and humidity exchange between airflow and rock wall in mine[D]. Tianjin: Tianjin University, 2008.

[2] 侯棋棕, 沈伯雄. 調熱圈半徑及其溫度場的數值解算模型[J]. 湘潭礦業學院學報, 1997,12(l):9-16.

HOU Qizong; SHEN Boxiong. The calculation of model the radius of control heat circle and its temperature field[J]. Journal of Xiangtan Mining Institute, 1997,12(1):9-16.

[3] 樊小利,張學博. 圍巖溫度場及調熱圈半徑的半顯式差分法解算[J]. 煤炭工程,2011(7):82-84.

FAN Xiaoli, ZHANG Xuebo. Semi explicit difference method for the temperature field of surrounding rock and the radius of t control heat circle[J]. Coal Engineering,2011(7):82-84.

[4] 魏亞興, 胡漢華, 何發龍, 等. 巷壁與空氣熱濕交換規律數值模擬研究[J]. 中國安全科學學報,2012,22(3): 42-47.

WEI Yaxing, HU Hanhua, HE Falong, et al. Numerical Simulation of heat-moisture exchange between tunnel wall and airflow[J]. China Safety Science Journal, 2012,22(3): 42-47.

[5] Moussi`ere S, Joussot-Dubien C, Guichardon P. Modelling of heat transfer and hydrodynamic with two kinetics approaches during supercritical water oxidation process [J]. J of Supercritical Fluids, 2007,43: 324-332.

[6] Shenglong Wang, Zhuang Wang, Hengxing Shang. Numerical simulation of ammonia phase change heat exchanger which used for composite air-cooling[J]. Energy Procedia, 2012,17:1086-1091.

[7] Wang Binbin. Comparative research on fluent and FDS’s numerical simulation of smoke spread in subway platform fire[J]. Procedia Engineering,2011,26:1065-1075.

[8] Jordi Adell, Jordi Adell, Antonio Bonafonte. Production of filled pauses in concatenative speech synthesis based on the underlying fluent sentence [J]. Speech Communication, 2012,54:459-476.

[9] Xingye Zhu, Shouqi Yuan, Hong Li, et al. Orthogonal tests and precipitation estimates for the outside signal fluidic sprinkler [J]. Irrigation and Drainage Systems, 2009,23(4):163-172.

[10] Hong Lu. Orthogonal experiment data analysis based on optimal discrimination plane and its application [J]. 2009 WRI World Congress on Computer Science and Information Engineering, CSIE, 2009:215-219.

[11] 何理, 蔣仲安, 鐘茂華. 正交實驗法優選煤炭自燃凝膠阻化劑及其應用[J]. 中國安全生產科學技術,2006(4):40-44.

HE Li, JIANG Zhongan, ZHONG Maohua. Study and application on optimum gel inhibitor for coal spontaneous combustion by orthogonal test method[J]. Journal of Safety Science and Technology, 2006(4):40-44.

[12] 阮波,阮慶,田曉濤,等. 淤泥質粉質黏土水泥土無側限抗壓強度影響因素的正交試驗研究[J]. 鐵道科學與工程學報,2013,10(6):45-48.

RUAN Bo, RUAN Qing,TIAN Xiaotao, et al. The study of the orthotropic test on cement-soil unconfinedcompressive strength of muddy silty clay[J]. Journal of Railway Science and Engineering, 2013,10(6):45-48.

(編輯陽麗霞)

Numerical simulation research on radius and temperature field of roadway heat-adjusting layer

HE Falong1,2,WEI Yaxing2,HU Hanhua2,WANG Juan3

(1.School of Energy and Safety Engineering, Tianjin Chengjian University, Tianjin 300384, China;2. School of Resources and Safety Engineering, Central South University, Hunan 410083, China;3. Zhonghui International Insurance Brokers Co. Ltd, Beijing 100022, China)

Abstract:To study the temperature field of surrounding rock during its heat transfer process, 25 sets of numerical experiment models were established to simulate the heat transfer process of heat-adjusting layer. The original rock temperature, heat-adjusting radius and thermal conductivity was selected as influence factors, and the roadway wall temperature was considered as target factor. According to the orthogonal analysis, it is concluded that the effects on the wall temperature were ranked in the order of original rock temperature > thermal conductivity > heat-adjusting layer radius. Based on the statistics analysis, the wall temperature thermodynamic calculation formula was fitted, and its correlation coefficient was 0.996. Finally, the ventilation time factor was broaden, then the relationship formula between heat-adjusting layer radius and ventilation time was fitted. The two calculation formulas can be used for evaluating roadway wall temperature.

Key words：numerical simulation; surrounding rock heat transfer; heat-adjusting layer ; wall temperature; orthogonal test; linear regression

中圖分類號：X936

文獻標志碼：A

文章編號：1672-7029(2016)03-0538-06

通訊作者：胡漢華(1957-)，男，湖南益陽人，教授，博士，從事礦山熱害控制與通風；E-mail:huhanhua@csu.edu.cn

收稿日期：2015-06-25