服務組合中保障公平性的信譽傳播算法

張 濤,馬建峰,莫 若,李 琦,習 寧

(西安電子科技大學計算機學院,陜西西安 710071)

?

服務組合中保障公平性的信譽傳播算法

張 濤,馬建峰,莫 若,李 琦,習 寧

(西安電子科技大學計算機學院,陜西西安 710071)

摘要:在面向服務的環(huán)境中,服務的不透明性、組合結(jié)構(gòu)的復雜性以及用戶評價的主觀性使得用戶難以對組件服務進行有效的信譽評估.針對此問題,提出適用于服務組合的信譽傳播算法,將復合服務的信譽評估值公平地傳播到各個組件服務.首先,將復合服務建模為Beta混合模型,通過最大期望算法學習復合服務中各個組件的責任及信譽度.其次,基于Shapley值的合作博弈模型計算各個組件服務對復合服務的貢獻度,確保所組合的各個服務不會受到額外的獎勵或懲罰.最后,理論分析與實驗結(jié)果表明該算法在保證公平性的前提下,能夠正確地將用戶提交的信譽評估層次化傳播到各個組件服務.

關(guān)鍵詞:面向服務的架構(gòu);服務組合;Web服務;信譽傳播;公平性

在面向服務架構(gòu)(Service-Oriented Architecture,SOA)中,服務表現(xiàn)為自治、平臺獨立的可重用計算實體,能夠以統(tǒng)一的標準進行描述、發(fā)布、發(fā)現(xiàn)和組合,為多機構(gòu)跨平臺軟件開發(fā)提供基礎.面向服務架構(gòu)的主要目標是在開放的網(wǎng)絡環(huán)境中利用Web服務自動化構(gòu)造滿足業(yè)務邏輯的復雜應用[1].然而,開放網(wǎng)絡內(nèi)在的不確定性使用戶需要承擔未知服務交互的風險.基于信譽的信任機制能夠?qū)Υ嬖诶娼换ヒ环降姆召|(zhì)量(Quality of Service,QoS)進行度量,激勵合法的服務行為,為用戶提供參考信息以降低與惡意服務交互的幾率,從而降低開放網(wǎng)絡中的交互風險[2-3].

然而,在服務組合中對組件服務的信譽評估十分困難.首先,由于服務的不透明性[4],用戶無法得知評價對象是原子服務或是復合服務,從而無法全面進行各個組件的信譽評估[5].其次,服務組合結(jié)構(gòu)的復雜性導致組合結(jié)構(gòu)服務質(zhì)量的多樣性,需要針對不同服務質(zhì)量特性建立不同的信譽計算規(guī)則[6].最后,即便用戶能夠掌握復合服務組合結(jié)構(gòu)及其服務質(zhì)量特性,其對各個服務組件評價的主觀性也導致難以實現(xiàn)組件服務信譽分配的公平性.因此,在服務組合中需要將用戶對復合服務的評估值公平傳播到所構(gòu)成該服務的各個組件.

目前對服務組合的信譽傳播問題已有了初步研究.文獻[7]最先定義服務組合中公平信譽傳播需滿足如下兩規(guī)則:組件服務不應由于其他組件較差的信譽而受到懲罰;組件服務不應由于其他組件較好的信譽而受到獎勵.并提出服務組件重要性與服務質(zhì)量一致性相結(jié)合的信譽分配算法.文獻[8]依據(jù)服務組件歷史信譽值和服務質(zhì)量,建立補償函數(shù)實現(xiàn)用戶評價值分解.文獻[9]結(jié)合信任趨勢與信譽評估值,建立層次結(jié)構(gòu)與水平結(jié)構(gòu)的信譽傳播方法.然而,上述工作均在服務組合結(jié)構(gòu)可觀測的前提下進行組件信譽度量,缺少對所提方案信譽傳播公平性的理論證明.此外,文獻[10]基于Shapley值的數(shù)學特性,提出公平保障的信譽傳播方法.其工作雖然在理論上保證了公平性,然而該方法假設服務組件服務質(zhì)量完全可觀察,并需要用戶提供對各個組件服務質(zhì)量的最佳值和最差值的數(shù)學期望,仍未解決服務不透明性所造成的信譽評估問題.

針對上述問題,筆者從服務組合的特征出發(fā),提出適應于Web服務組合的公平信譽傳播算法(FGRP).首先針對服務不透明性及組合結(jié)構(gòu)特點,將復合服務建模為Beta混合模型,利用最大期望算法學習出各個服務組件責任和信譽度.其次,基于Shapley值的合作博弈模型計算組件貢獻度,并依據(jù)該貢獻度將用戶對復合服務的主觀評價層次化分配到各個服務組件,保障信譽傳播的公平性.

1 FGRP信譽傳播算法

1.1 服務信譽表示

面向服務架構(gòu)的主要特性是利用平臺獨立的服務,通過組合的方式為用戶提供增值的服務.復合服務通常作為整體與用戶交互.在特定情況下(如遺產(chǎn)系統(tǒng)),服務以黑盒的方式提供給用戶,用戶難以分析其組合邏輯的依賴關(guān)系.為了評估各個組件服務對復合服務信譽的貢獻度,算法用Beta概率模型[11]建模所交互服務的信譽記錄.

Beta概率模型將信譽表示為二元證據(jù)模型θ=〈α,β〉(α≥0,β≥0),其中α和β分別表示滿意和未滿意的交互次數(shù).其概率密度函數(shù)表示為

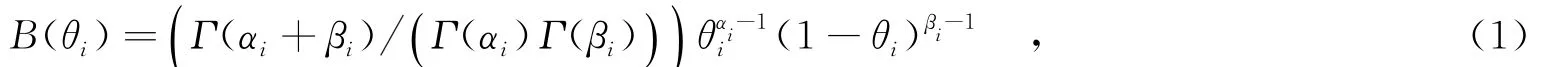
服務si的信譽表示為Beta概率模型的數(shù)學期望,即

1.2 組件服務責任及信譽的統(tǒng)計學習

不透明性表示用戶無法區(qū)分所交互的服務是原子服務,或是多個服務所組成的復合服務,從而無法對組件服務直接進行信譽評估.為了將復合服務的評價值公平地分配到各個組件服務,在獲得復合服務信譽的觀察之后,利用有限混合模型統(tǒng)計學習出各個組件的責任和信任度,從而解決服務的不透明性.

有限混合模型將每個數(shù)據(jù)對象建模為混合分支,合并不同混合分支為描述整個數(shù)據(jù)特征的混合分布,通過統(tǒng)計實現(xiàn)數(shù)據(jù)識別.筆者用Beta混合模型建模復合服務的信譽混合.在由K個組件服務構(gòu)成的服務組合中,組件服務si建模為參數(shù)θi=〈αi,βi〉的Beta概率模型,則復合服務的Beta混合表示為

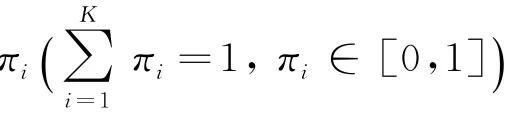
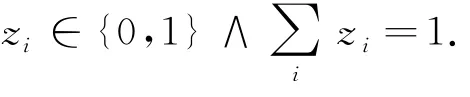
最大期望算法通過期望步(E-step,E步)和極大化步(M-Step,M步)兩過程的不斷迭代,最終收斂到似然函數(shù)的最優(yōu)解,其執(zhí)行流程如下.

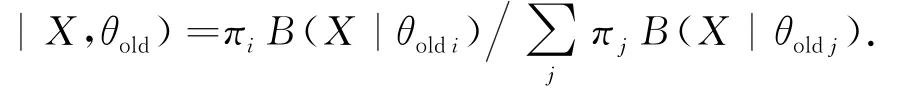
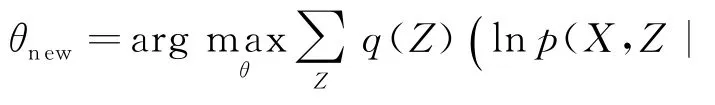
重復E步和M步,直至參數(shù)θnew下對數(shù)似然函數(shù)收斂.此時,參數(shù)πn ew i和θnew i分別表示當前復合服務中組件服務si的責任和信譽度的統(tǒng)計值.

1.3 基于Shapley值的貢獻度計算

算法FGRP引入符號ωi,ωi∈(0,1],表示組件服務si在服務組合中執(zhí)行的概率.服務組合結(jié)構(gòu)主要包括確定組合模式(包括順序、循環(huán)、并發(fā)等)和概率組合模式兩類[4,6].在確定組合模式中,各個組件按照組合順序依次執(zhí)行,其ωi=1.在概率組合模式中,組件執(zhí)行概率表示為責任值歸一化后的比率.例如,假設服務集si,j∈{si,1,…,si,m},構(gòu)成概率模型,其責任值πi,j∈{πi,1,…,πi,m},則概率ωi,j∈{ωi,1,…,ωi,m}=πi,j/ (πi,1+…+πi,m).在得到組件服務執(zhí)行概率及證據(jù)模型后,服務組件的組合信譽值根據(jù)文獻[12]提出的聚合規(guī)則進行計算.

算法FGRP依據(jù)組件服務si對復合服務的貢獻度Δi(c)進行信譽傳播.為了保證公平性,算法利用合作博弈理論的Shapley值[13]計算各個組件服務si的貢獻Δi(c),表示為

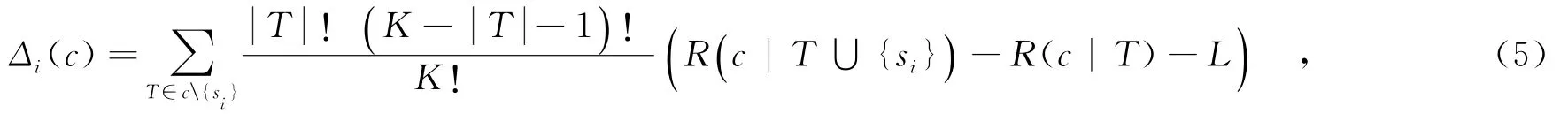
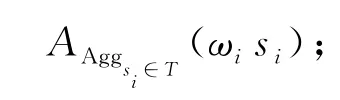
1.4 信譽傳播

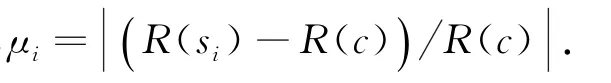
根據(jù)上述分析,算法FGRP在保障公平性的基礎上,能夠有效地解決由服務不透明性、組合結(jié)構(gòu)復雜性和用戶評價主觀性所造成的信譽傳播問題,其算法流程如下:

步驟1(服務不透明性) 通過觀察值學習各個組件的責任及信譽度,見1.2節(jié).

步驟2(組合結(jié)構(gòu)復雜性) 根據(jù)Shapley值計算組件服務在組合結(jié)構(gòu)下對復合服務的貢獻度,見1.3節(jié).

步驟3(用戶評價主觀性) 將用戶的主觀評價根據(jù)貢獻度傳播到組件服務之上,見本節(jié)前段.若該組件仍是復合服務,則轉(zhuǎn)至步驟1.

2 FGRP分析

2.1 FGRP特性分析

算法FGRP基于Shapley值進行組件服務的信譽分配,將用戶對復合服務的主觀信譽評估公平傳播于所組成的各個服務組件.因此,算法FGRP能夠繼承Shapley值的特性.

對稱性(Symmetry) 對于?T∈c{si,sj},若R( c|T∪{si} )=R ( c|T∪{sj} ) ,則Δi(c)=Δj(c).

貢獻平衡性(Balanced Contribution) 對于?si,sj∈c,Δi(c)-Δi( c|c{sj} )=Δj(c)-Δj( c|c{si} ),其中Δi(c|T)表示在復合服務c的組合結(jié)構(gòu)中,組件服務si對給定子集T的貢獻度.平衡性確保各個組件的貢獻度在各個組件中能夠平均分配,從而保證服務組件的信譽傳播的公平性.

2.2 FGRP公平性分析

通過組件信任度的變化證明算法FGRP的公平性.在證明中,令Rt(s)、Rt′(s)和et(s)、et′(s)分別表示在連續(xù)等長時間t、t′時組件服務s的信譽值和證據(jù)數(shù),則信譽差和證據(jù)差分別表示為ΔR(s)=Rt(s)-Rt′(s)和Δe(s)=et(s)-et′(s).首先考慮當Δe(s)=0,ΔR(s)＞0時的信譽變化情況.對于任意的組合結(jié)構(gòu),當單個組件信譽提升時,以下命題始終成立.

命題1 組件服務si信譽值的提升不會導致復合服務c信譽值的下降[8],即

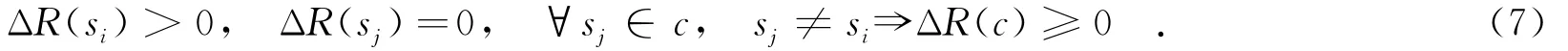
同時,對于?sj∈c,sj≠si,ΔR(sj)=0時,由式(7)可得對稱性表示若不同組件與其他組件組合時信譽度相同,則其貢獻度相同.

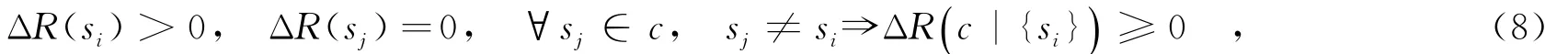
其中,ΔR(c|si)=0,表示組件服務si的信譽提升并未導致復合服務c的信譽提升.例如,組件服務sA和sB以概率模式組成復合服務c,并且ΔR(sA)＞0.若復合服務中sA的執(zhí)行概率較低,則存在特定時間t中未提升復合服務信譽的可能性,從而ΔR(c|sA)=0.為了表示復合服務信譽值改變,提出有效信譽提升的定義,當信譽下降時能夠得出類似結(jié)論.

定義1(有效信譽提升) 組件服務si的有效信譽提升表示其信譽提升導致復合服務c的信譽提升,即

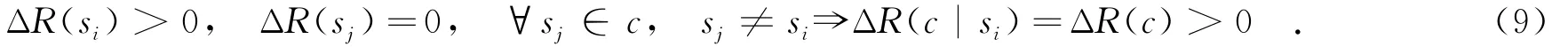
根據(jù)定義1,可得如下推論.

推論1 給定復合服務c={s1,…,sK}以及T∈c{si},若R(si)＞R(c),則

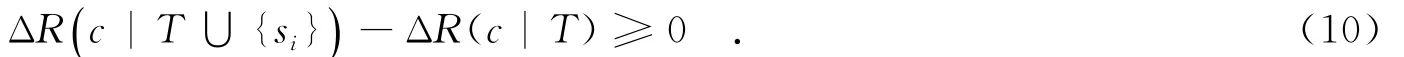
下面,考慮組件服務信譽的改變對信譽傳播配額的影響,并證明算法FGRP的公平性.

引理1 若組件服務si具有的有效信譽提升,則v(si)＞Ru.

證明 令T∈c{si},考慮如下兩種情況:

情況1 若T=?,則ΔR( c|T∪{si} )-ΔR(c|T)=ΔR( c|{si} )-ΔR(c|?)=ΔR( c|{si} )＞0;

情況2 若T≠?,根據(jù)推論1,可得ΔR( c|T∪{si} )-ΔR(c|T)≥0.

根據(jù)式(5),可得Δi(c)＞0.因此,由式(6),可得v(si)＞Ru.證畢.

引理2 對于?sj∈c,sj≠si,若Rt(si)＜Rt′(si),且Rt(sj)=Rt′(sj),則vt(si)＜vt′(si).

證明 令T∈c{si},已知?sk∈c,Δe(sk)=0,則ΔR(c|si)＜0且ΔR(c|sj)=0.考慮如下兩種情況:

情況1 若T=?,則Rt( c|T∪{si} )-Rt′(c|T∪{si} )=Rt(c|si)-Rt′(c|si)＜0;

情況2 若T≠?,根據(jù)命題1,可得Rt( c|T∪{si} )-Rt′(c|T∪{si} )≤0.

此外,對于?sj∈c,sj≠si,已知Rt(sj)=Rt′(sj),則對于?T,可得Rt(c|T)=Rt′(c|T).由

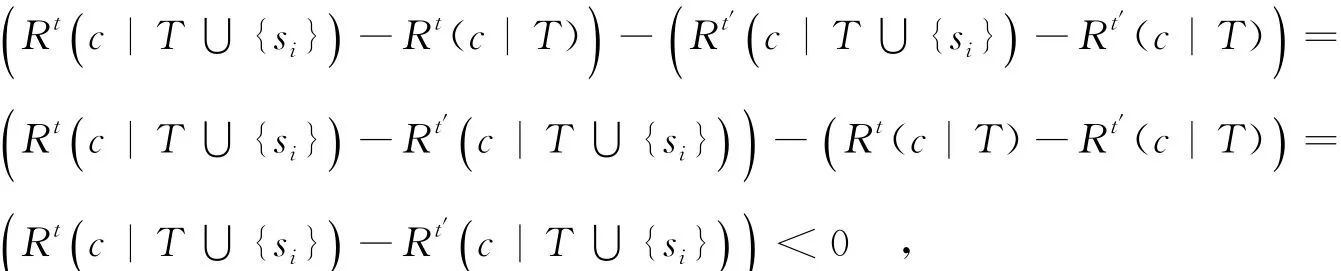
引理3 ?sj∈c,sj≠si,若Rt(si)＞Rt′(si),且Rt(sj)=Rt′(sj),則vt(si)＞vt′(si).

引理4 ?sj∈c,sj≠si,若Rt(si)=Rt′(si),且Rt(sj)=Rt′(sj),則vt(si)=vt′(si).

引理3和引理4的證明與引理2的證明類似,在此省略.

上述引理證明了在證據(jù)數(shù)目不變(Δe(s)=0)的條件下信譽傳播的公平性.當證據(jù)數(shù)Δe(s)≠0時,首先假設單個組件的證據(jù)數(shù)增加或減少時信譽傳播配額的變化下的公平性,之后利用歸納法證明當多個組件證據(jù)數(shù)的信譽傳播的配額變化.其證明與引理2的證明類似,在此省略.

定理1 在服務組合中,所提出算法能夠公平地將信譽傳播到組件服務之中.

證明 根據(jù)上述引理,定理1成立.

3 仿真評估

3.1 實驗環(huán)境

以圖1為例對不同結(jié)構(gòu)下算法FGRP信譽傳播的公平性進行實驗評估(實驗以順序結(jié)構(gòu)為例說明確定結(jié)構(gòu)下的信譽傳播結(jié)果).在圖1中,假設用戶希望將漢語翻譯至盧森堡語,但網(wǎng)絡中并不存在直接的翻譯器.服務提供商通過組合漢語至英語(Chi-to-Eng)、英語至德語(Eng-to-Deu)、德語至盧森堡語(Deu-to-Lux)的組件服務實現(xiàn)翻譯功能.同時,存在3個不同服務商GOG、MIC和BAI來提供英語至德語的翻譯服務,其調(diào)用概率分別為60%、20%和20%.

圖1 漢語至盧森堡語翻譯服務

兩組實驗分別對不同組合結(jié)構(gòu)進行獨立實驗評估.每組實驗生成100組觀察值,并利用文獻[14]方法對最大期望算法進行初值選取以減少組件責任及信譽度計算的誤差.同時,實驗與特征類似的文獻[7]方案進行對比.對比中令用戶評價值Ru=0.7,Shapley值計算常數(shù)L= R(c).其他參數(shù)與實驗結(jié)果如表1和表2所示.

表1 確定組合模式的信譽傳播

表2 概率組合模式的信譽傳播

3.2 評估結(jié)果

表1描述圖1中順序模式服務s1、s2和s3信譽傳播實驗結(jié)果,其包含信譽評估較好的服務s1和較差的服務s3以及中性服務s2.如表1所示,在算法FGRP中s1始終獲得正向貢獻度,而s3獲得負向貢獻度.此外,當中性服務證據(jù)值改變時(第2行數(shù)據(jù)),復合服務信譽度向其逼近,其他服務的貢獻度因此減少,而算法FGRP能夠有效地反映出貢獻改變的情況并計算正確的傳播值.最后,當特定組件信譽改變時(第3行數(shù)據(jù)),其余組件的貢獻度也會相應改變,而在文獻[7]提出的算法中,在各個組件的信譽度不變而證據(jù)值變化時,其傳播值不變,從而無法正確表征組件的貢獻度.

對于確定模式組合結(jié)構(gòu),實驗中各算法統(tǒng)計學習的最大誤差為22%.這是由于在確定性模式中,Beta混合模型的概率分布疊加在特定觀察值下呈現(xiàn)單峰分布,從而無法很好地進行統(tǒng)計學習.由于算法引入一致性因子μ,μ∈(0,1),在一定程度上能夠減少誤差帶來的影響,實現(xiàn)公平的信譽傳播.此外,表1還能夠證明Shapley值的有效性,即正向貢獻和與負向貢獻和始終相等.

表2描述了圖1中概率模式服務s4、s5和s6信譽傳播的實驗結(jié)果.由于概率組合模式特性與最大期望算法的乘法疊加特性類似,在算法中統(tǒng)計學習的最大誤差僅為4.6%.表2結(jié)果與表1結(jié)果類似,均能夠很好地反映各個組件貢獻度及信譽傳播的公平性.而文獻[7]所提出算法由于不支持概率組合模式,其傳播值無法表征信譽傳播的公平性以及組件證據(jù)數(shù)變化時傳播值變化的正確性.

3.3 方案對比

算法FGRP與相關(guān)信譽傳播算法的對比如表3所示.首先,FGRP通過統(tǒng)計學習方法對組件的責任及信譽度進行學習,不依賴已有算法對服務組件信譽或服務質(zhì)量值可觀察性的假設,從而解決了不透明性問題.其次,算法FGRP不僅考慮文獻中的確定性模型,而且支持對部分工作[7-9]中缺少的概率模式的信譽傳播,從而全面解決了服務組合結(jié)構(gòu)的復雜性問題.再次,FGRP無須用戶對最優(yōu)和最差情況組件的服務質(zhì)量值進行估計[10],將用戶對復合服務的評價值公平傳播到各個組件,從而解決了用戶評價的主觀性問題.最后,筆者基于Shapley值特性對算法FGRP進行證明,確保所提算法的公平性.

表3 信譽傳播方案對比

4 結(jié)束語

針對服務的不透明性、組合結(jié)構(gòu)的復雜性以及用戶評價的主觀性所造成的信譽傳播問題,筆者提出一種適用于服務組合的公平信譽傳播算法,即FGRP.該算法具有如下特征:基于Beta混合模型對組件責任及信譽度學習,解決服務的不透明性;對確定組合模式與概率組合模式分別建模,解決服務結(jié)構(gòu)組合的復雜性;基于合作博弈Shapley值進行服務貢獻計算,消除用戶評價的主觀性.算法FGRP在無須用戶提供服務質(zhì)量估計值的基礎上,實現(xiàn)了復合服務到組件服務信譽的層次化公平傳播.理論分析與實驗結(jié)果均能夠證明所提方法的合理性和有效性.

下一步研究工作的重點首先在于提高信譽傳播的精確性,其主要來源于兩個方面:減少由于概率疊加所造成的統(tǒng)計誤差;服務信譽變化的動態(tài)性對信譽傳播變化的影響.其次,對于海量服務的貢獻度計算,Shapley值在計算時需要考慮所有組合情況,因而存在開銷過大的問題.所以,提高計算性能也是將來研究需要考慮的問題之一.

參考文獻:

[1]PAPAZOGLOU M P,TRAVERSO P,DUSTDAR S,et al.Service-oriented Computing:a Research Roadmap[J].International Journal of Cooperative Information Systems,2008,17(2):223-255.

[2]J?SANG A,ISMAIL R,BOYD C.A Survey Of Trust And Reputation Systems For Online Service Provision[J].Decision Support Systems,2007,43(2):618-644.

[3]孟憲佳,馬建峰,盧笛,等.面向可信和行為模式匹配的兩層服務選擇方法[J].西安電子科技大學學報,2014,41(4): 198-204.MENG Xianjia,MA Jianfeng,LU Di,et al.Trust and Behavioral Modeling Based Two Layer Service Selection[J].Journal of Xidian University,2014,41(4):198-204.

[4]ZHANG T,MA J F,SUN C,et al.Service Composition in Multi-domain Environment under Time Constraint[C]// Proceedings of the IEEE 20th International Conference on Web Services.Piscataway:IEEE Computer Society,2013: 227-234.

[5]ZHANG T,MA J F,XI N,et al.Trustworthy Service Composition in Service-oriented Mobile Social Networks[C]// Proceedings of the IEEE 21th International Conference on Web Services.Piscataway:IEEE Computer Society,2014: 684-687

[6]ZHANG T,MA J F,LI Q,et al.Trust-based Service Composition in Multi-domain Environments under Time Constraint[J].Science China Information Sciences,2014,57(9):092109(16).

[7]NEPAL S,MALIK Z,BOUGUETTAYA A.Reputation Propagation in Composite Services[C]//Proceedings of the IEEE International Conference on Web Services.Piscataway:IEEE,2009:295-302.

[8]Da SILVA I,ZISMAN A.Decomposing Ratings in Service Compositions[C]//Lecture Notes in Computer Science:8274 LNCS.Heidelberg:Springer Verlag,2013:474-482.

[9]SADEGHI R,AZGOMI M A.A Method for Fair Propagation of User Perceptions for Trust Management in Composite Services[J].Service Oriented Computing and Applications,2015,9(2):157-176.

[10]LIU A,LI Q,ZHOU X F,et al.Rating Propagation in Web Services Reputation Systems:A Fast Shapley Value Approach[C]//Lecture Notes in Computer Science:8421 LNCS.Heidelberg:Springer Verlag,2014:466-480.

[11]HANG C W,SINGH M P.Trustworthy Service Selection and Composition[J].ACM Transactions on Autonomous and Adaptive Systems,2011,6(1):5-22.

[12]LI L,WANG Y.Trust Evaluation in Composite Services Selection and Discovery[C]//Proceedings of the IEEE International Conference on Services Computing.Piscataway:IEEE Computer Society,2009:482-485.

[13]SHAPLEY L S.Theory of GamesⅡ[M].Princeton:Princeton University Press,1953:307-317.

[14]BOUGUILA N,ZIOU D,MONGA E.Practical Bayesian Estimation of a Finite Beta Mixture through Gibbs Sampling and Its Applications[J].Statistics and Computing,2006,16(2):215-225.

(編輯:郭 華)

Fairness-guaranteed reputation propagation in Web service composition

ZHANG Tao,MA Jianfeng,MO Ruo,LI Qi,XI Ning
(School of Computer Science and Technology,Xidian Univ.,Xi’an 710071,China)

Abstract:In service-oriented environment,it is difficult to evaluate component services because of the opaque characteristic of composite services,the complex invocation structures and the subjective reputation rating of service consumers.To address these issues,this paper proposes a reputation propagation algorithm for service composition,in which the subjective ratings can be fairly propagated to each component service.The algorithm first models service composition as the Beta-mixture,and learns the reputation and responsibility of each component by the EM algorithm.Then,based on the characteristics of Shapley values in cooperative gaming theory,the algorithm computes the contribution of each component to its composition,ensuring that no component would obtain extra rewards or punishments.Finally,theoretical analysis and experimental results demonstrate the fairness of the algorithm to hieratically propagate the consumer’s rating to each component service.

Key Words:service-oriented architecture;service composition;Web services;reputation propagation; fairness

作者簡介:張 濤(1986-),男,西安電子科技大學博士研究生,E-mail:tzhang@stu.xidian.edu.cn.

基金項目:長江學者和創(chuàng)新團隊發(fā)展計劃資助項目(IRT1078);國家自然科學基金委員會-廣東聯(lián)合基金重點基金資助項目(U1135002);國家科技部重大專項資助項目(2011ZX03005-002);國家自然科學基金資助項目(61370078)

收稿日期:2014-10-17 網(wǎng)絡出版時間:2015-05-21

doi:10.3969/j.issn.1001-2400.2016.02.013

中圖分類號:TP309

文獻標識碼:A

文章編號:1001-2400(2016)02-0070-07

網(wǎng)絡出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20150521.0902.010.html