基于混沌的ATP車載設備故障率預測

康仁偉， 王俊峰， 程劍鋒， 劉雅晴

(1. 中國鐵道科學研究院 通信信號研究所，北京 100081；2. 北京交通大學 軌道交通控制與安全國家重點實驗室，北京 100044)

ATP車載設備是保證列車運行安全的關鍵裝備。全路在用的ATP類型有300T，300S，300H，200H，200C和C3D。隨著設備本身屬性、走行公里、自然條件等因素的變化，各種類型ATP運行故障率變化趨勢不盡相同。目前，ATP車載設備備品備件的配置大多依據經驗，各備件配置數量短期內恒定不變，不能隨著設備故障的變化而動態調整。結果是部分設備儲備量不足影響故障維修，而部分設備過多儲備又造成資源浪費。如果能預測ATP設備短期內的故障趨勢，則可以有針對性地提前采購儲備ATP備件，緩解設備儲備量不足和過剩的矛盾。 用于短時預測的方法主要分為基于確定數學模型的預測方法、無明確數學模型的預測方法和組合思想的預測方法3類[1]。其中，混沌理論屬于無明確數學模型的方法，用于研究非線性動力系統的規律，不需建立主觀模型，直接從數據中挖掘隱藏的客觀規律而進行預測，預測精度和可信度均很高[1]。混沌理論已經用于鐵路貨物運量預測[2-3]，短時交通流的分析和預測[1,4-5]，股票預測[6]等多個領域，為數據未來的變化趨勢提供了科學有效的參考依據。目前對于ATP車載設備運行故障趨勢的預測未見相關文獻。本文采用混沌理論，從ATP設備歷史故障數據的角度，深入挖掘分析故障數據的特點，短時預測ATP設備的故障趨勢，為合理優化配置ATP備品備件提供科學參考。

1 ATP車載設備運行故障特點

衡量ATP設備運用質量的一個重要指標是百萬公里故障率，即ATP隨著列車運行一百萬公里發生的故障次數。圖1為2013年8月至2014年12月，全路6種類型ATP設備按月統計百萬公里故障率變化趨勢圖。

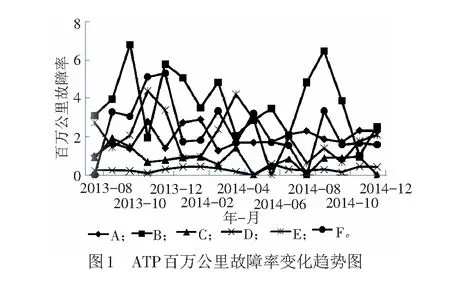
圖1中，6種設備類型分別記做A～F，由圖1可得ATP設備運行故障呈現如下特點：

(1)非線性；(2)動態時變，某種程度上的隨機性；(3)序列包含ATP車載設備運行的行為特征；(4)貌似無規則性。

混沌理論非常適合研究整體呈現確定性，但是又具有某種隨機性的動態變化系統[7]，吻合ATP設備的故障特點。因而，用混沌理論對ATP設備百萬公里故障率一維時間序列進行相空間重構，從高維的角度挖掘設備故障數據蘊藏的潛在規律，短期預測ATP設備故障未來的變化趨勢。

2 混沌理論

混沌是確定性的非線性系統產生的一種貌似隨機的，實際上隱含著潛在規律的動態行為。

Li-Yorke混沌定義[7-8]：[a,b]上的連續自映射f，存在不可數子集S?[a,b]，若滿足以下條件，則稱其具有混沌特性：

(1)S中無周期點；

(2) 對?x,y∈S，有

(3) 對?x,y∈S，有

(4) 對?x∈S和f的任意周期點y，有

Li-Yorke混沌定義刻畫了混沌系統的3個特征[7]，即非周期、對初始條件的敏感性和有界。

混沌狀態空間長期動態行為的幾何形式用吸引子描述，其中，混沌吸引子[8]是軌道不穩定和相空間收縮兩種因素共同作用的極限集合。

3 基于混沌理論的ATP設備故障率預測

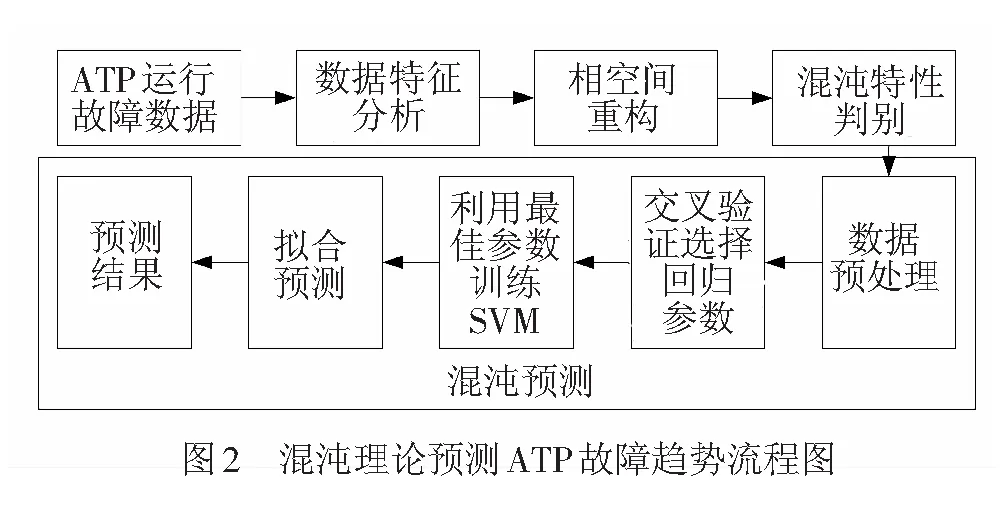
ATP車載設備百萬公里故障率一維時間序列難以挖掘其潛在規律，因而將其通過相空間重構理論映射到高維空間，然后判斷其是否具有混沌特性。若有，則利用支持向量機模型預測ATP運行故障短期內的變化趨勢。整體思路見圖2。

3.1 相空間重構

ATP百萬公里故障率是長度為n的一維時間序列為

X=xi|i=1,2,…,n

( 1 )

以某種類型的ATP設備為例(以下記做ATP-X)，定義

( 2 )

式中:aj表示第j天全路ATP-X設備發生的故障件數；sj表示第j天全路ATP-X設備的走行公里。

數據統計起始日期為2012年7月1日，結束日期為2014年12月31日。因為是累積求和再進行計算，隨著時間的遞增，數據值相對更穩定，剔除前面部分誤差較大的數據，選取較穩定的數據作為樣本，即X={0.443 306, 0.441 469, 0.439 659,…}，樣本容量n=717，其時間序列見圖3。

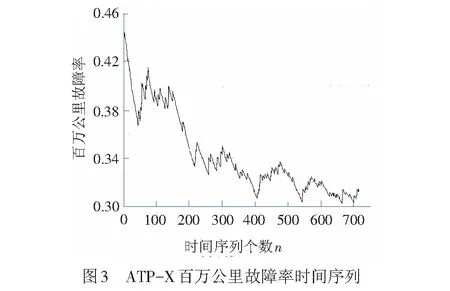
圖3中縱坐標表示隨著時間推移的序列個數，可見，ATP-X的百萬公里故障率整體呈下降趨勢，局部在小范圍內波動。

除此之外，很難再得到ATP-X百萬公里故障率的其他變化規律。因而，將百萬公里故障率一維時間序列擴展到高維空間，且保證高維空間與原百萬公里故障率時間序列的微分同胚性，從而在高維空間恢復混沌吸引子，挖掘一維時間序列的變化規律。嵌入定理[3,7]表明，只要適當選取延遲時間τ和嵌入維數m，ATP百萬公里故障率時間序列的幾何特性與重構m維空間的幾何特性等價，兩者具有相同的拓撲結構。

對X采用延遲嵌入的方式進行重構，得到軌跡矩陣Y

( 3 )

式中:τ為延遲時間;m為嵌入維數。每一列表示一個相點。記M=n-m-1τ。

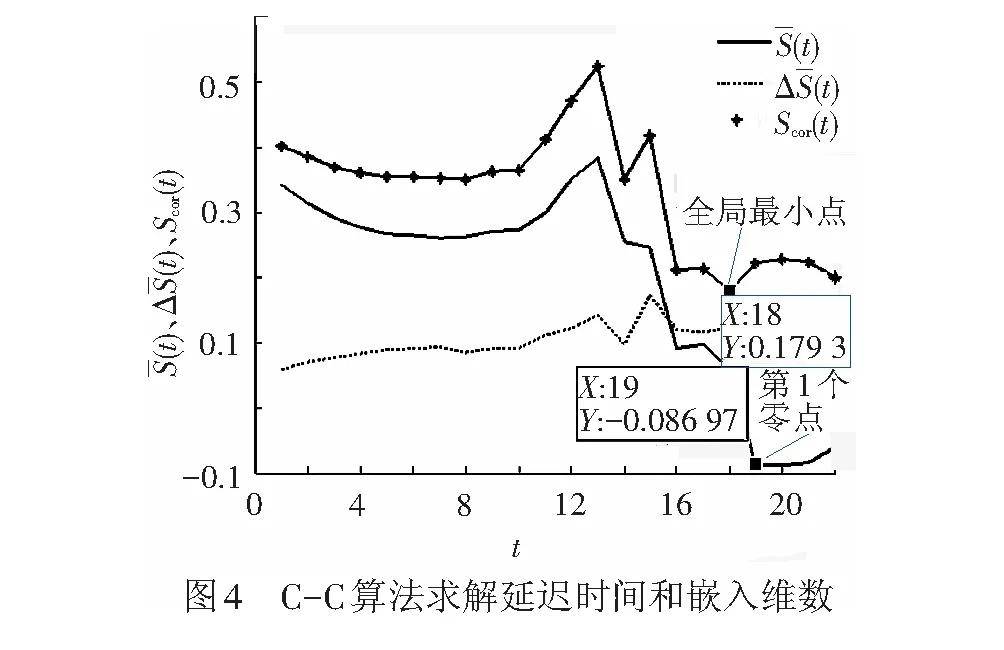
采用C-C算法[2-3,9]同時估計延遲時間τ和嵌入維數m。

將時間序列X=xi|i=1,2,…,n劃分為t個不相交的子序列[3,7]，長度為l=[n/t]([*]表示取整)

{x(1),x(t+1),x(2t+1),…}

{x(2),x(t+2),x(2t+2),…}

?

{x(t),x(t+t),x(2t+t),…}

定義每個子序列的統計量

S(m,n,r,τ)=

( 4 )

式中:Cl表示第l個子序列的關聯積分。

定義

C(m,n,r,τ)=

( 5 )

式中:r為鄰域半徑;M為相點數目;θ(*)為Heaviside單位函數。

定義

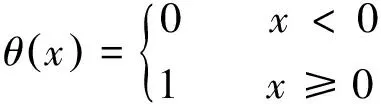
( 6 )

相點Xi與最接近的相點Xj間的歐式距離用無窮范數表示

d=‖Xi-Xj‖=

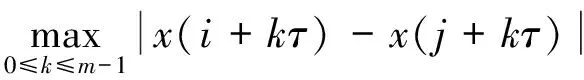
( 7 )

當n→時，記做

S(m,r,τ)=

( 8 )

S(m,r,τ)～τ反映了時間序列的自相關性。

定義

ΔS(m,τ)=

maxS(m,ri,τ)-minS(m,rj,τ)

( 9 )

為度量S(m,r,τ)～τ對所有鄰域半徑r的最大偏差。

本文采用改進的C-C算法[7]，定義

ΔS(m,τ)=stdS(m,r,τ)

(10)

式中:std{*}表示S(m,r,τ)的均方差。

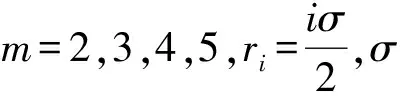
設

求得延遲時間和嵌入維數后，即可將長度為717的一維時間序列X相空間重構為2×698的高維矩陣Y。

3.2 混沌特性判別

對ATP-X百萬公里故障率時間序列X相空間重構后，應該判斷該序列是否具有混沌特性。本文采用Lyapunov指數法[4,7,10]判斷混沌特性。格里波基證明[7]，只要最大Lyapunov指數λ大于0，系統就存在混沌特性。

目前求解最大Lyapunov指數的方法主要有Wolf法[1,7]、Jacobian法[1,7]、P-范數法[7]和小數據量法[5]。Wolf法計算誤差較大，魯棒性、穩定性較差。Jacobian法適用于噪聲較大的序列。P-范數法計算量大，操作困難。小數據量法計算量小，易操作，對小數據可靠。如下采用小數據量法計算最大Lyapunov指數。

具體步驟[5,8]如下:

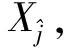
(11)

式中：j=1,2,…,M;P為時間序列的平均周期。

Step2計算相點Xj經過iΔt演化時間后的距離

(12)

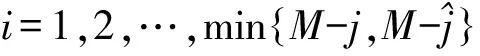
Step3據文獻[5]

lndji≈lndj0+λiΔt

(13)

最大Lyapunov指數為上式直線的斜率，可通過最小二乘法逼近得到，即

(14)

式中:q為非零dji的個數;yi表示對每個i，所有j的lndji的平均值。

根據3.1節的結果：τ=19，m=2。本文以全路范圍內同一種車載設備為例，綜合考慮車載設備日常的運用檢修和高級檢修，設置ATP-X百萬公里故障率時間序列平均周期P=180。求取最大Lyapunov指數結果見圖5。最大離散步進時間設為50。

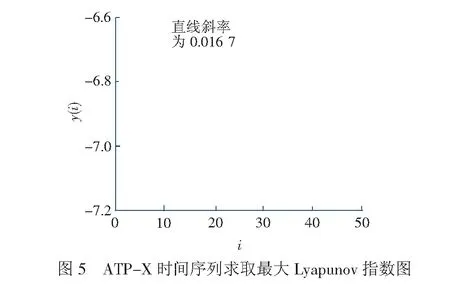
圖5中，實線表示y(i)的值，虛線表示Step3中的直線，其斜率為0.016 7，即最大Lyapunov指數λ=0.016 7>0。因而，ATP-X型車載設備百萬公里故障率時間序列具有混沌特性，可以采用混沌理論對其未來變化趨勢進行短期預測。

3.3 混沌預測

對ATP百萬公里故障率一維時間序列相空間重構和混沌特性判別之后，在高維空間中挖掘ATP潛在的故障變化規律，進而預測ATP運行故障的變化趨勢和變化的范圍空間。

(1) 預測原理

ATP-X車載設備百萬公里故障率X={xi|i=1,2,…,n},相空間重構之后得到的M個相點為

X1=x1,x1+τ,…,x1+m-1τ

X2=x2,x2+τ,…,x2+m-1τ

?

XM=xM,xM+τ,…,xM+m-1τ

(15)

進一步演化之后的相點為

XM+1=

{xM+1,xM+1+τ,

…,xM+1+m-1τ}

(16)

上式中的元素xM+1+m-1τ正是需要預測的下一個序列點xn+1。

相點Xi與xi+1+m-1τ之間有某種確定的復雜函數關系[7]，即

xi+1+m-1τ=fXi

(17)

找出XM的K個鄰近點XMi(i=1,2,…,K)，利用支持向量機SVM(Support Vector Machine)[11]的逼近能力，用一個最優函數擬合

fXMi=xMi+1+m-1τ

若確定fx，則有

xn+1=xM+1+m-1τ=

fXM

(18)

同理，可預測xn+2,xn+3,…。

SVM是一種基于統計學習理論的有效的機器學習方法，根據有限的樣本信息在學習能力和模型的復雜性之間尋求最佳折中，具有泛化能力強、容易訓練、沒有局部極小值等優點[11-12]。本文需要確定函數f(x)，顯然是一個回歸問題。ε-SVR(ε-Support Vector Regression)支持向量回歸模型屬于SVM的一種，訓練的目標為y-f(x)≤ε。

如果指定不敏感度ε，就得到ε-SVR，即

s.t.

yi-w,Φ(xi)-b≤ε+ξi

(19)

其解為

(20)

式中:c是懲罰系數，其他參數見文獻[11]。

至此，利用SVR對ATP百萬公里故障率時間序列做混沌預測的模型見圖6。

(2) 數據歸一化處理

選取第1～M-1個相點作為自變量，選取第2～M個相點的最后一個元素作為因變量。前期粗略預測發現，對矩陣Y的數據不做處理直接作為輸入預測準確率較低。于是，分別對自變量和因變量按照如下映射進行歸一化預處理

(21)

這樣，作為SVR模型輸入的矩陣Y的元素被規整到[0,1]范圍內，以提高預測精度。

(3) SVR最優參數選擇

首先給出參數評價指標：

平均平方誤差

(22)

平方相關系數

r2=

(23)

式中:n表示樣本數。

采用SVR解決回歸函數f(x)的估計問題，必須確定不敏感度ε、懲罰系數c和核函數參數g三個參數[12]。不敏感度ε決定了回歸函數對樣本數據不敏感區域的范圍及支持向量的個數；懲罰系數c是對經驗風險和置信范圍的折中，表示對超出誤差ε的樣本的懲罰程度。本文選用高斯RBF核函數[12]

K(x,y)=exp-g‖x-y‖2

(24)

式中:g表示核函數。

首先，設定不敏感度ε=0.01。

然后，通過一種交叉驗證CV(Cross Validation)[13]的方法，將懲罰系數c和核函數參數g在2的指數范圍網格內進行查找，尋找一定意義下最佳的c和g。

粗略確定c和g的尋優范圍，讓其取值變化都為2-10，2-9，…，210。粗略選擇結果見圖7。最佳c=0.353 55,g=2.828 4，最小的MSE=0.002 300 6。

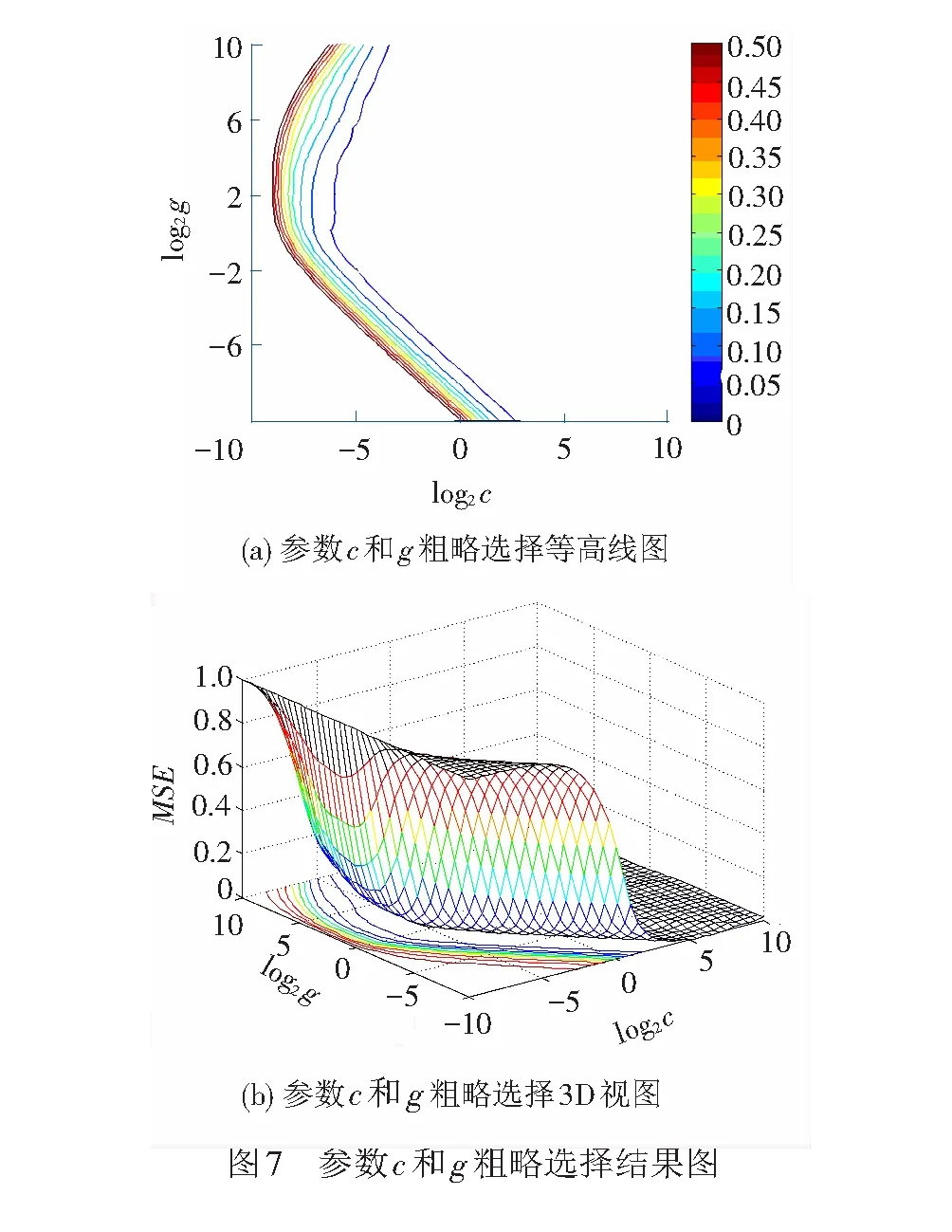
圖7中，x軸表示c取以2為底的指數后的值，y軸表示g取以2為底的指數后的值，等高線和3D視圖的z軸表示取相應的c和g后對應CV方法的平均平方誤差。

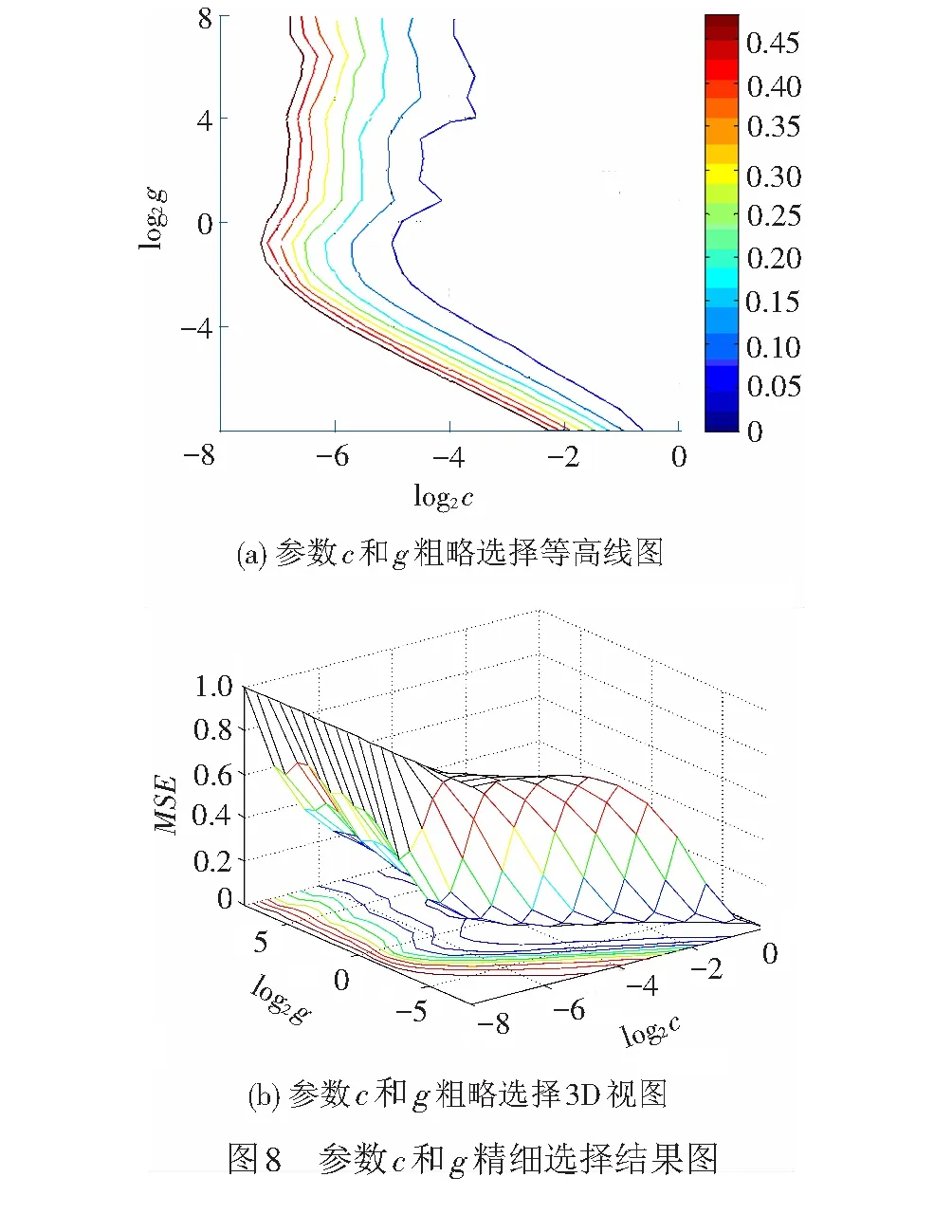
由圖7可見，c的范圍可縮小至2-8～20，g的范圍可縮小至2-8～28。如此，得出參數c和g的精細選擇結果如圖8所示。最佳c=0.574 35,g=1.741 1，最小的MSE=0.002 226 2。其最小的MSE值小于粗略選擇的最小MSE值，表明精細選擇參數結果更優。

(4) 預測結果

根據前文得到的最佳參數c和g訓練SVR，按照圖6的輸入輸出關系，得出一個模型回歸擬合f(x) ，據此預測ATP-X時間序列X后200條數據，驗證模型的準確性。

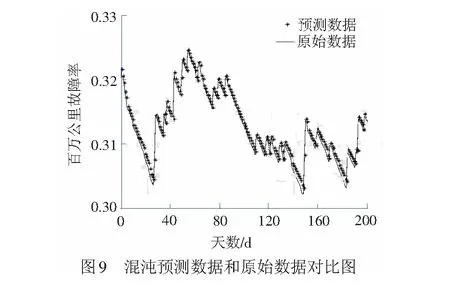
圖9為混沌預測數據和原始數據的對比，混沌預測數據和原始數據基本吻合，表明混沌預測方法適用于ATP車載設備的百萬公里故障率趨勢預測。如果預測呈上升趨勢，那么，鐵路電務部門應該提前儲備足夠的ATP-X的備品備件，并且在日常維修中，應該重點檢查或監測ATP-X的設備狀態，統籌調配電務資源，做到預防維修。

據文獻[2]，最大Lyapunov指數λ的倒數T=1/λ表示混沌系統最長預測時間。由前節可得λ=0.016 7，故T=1/λ≈59。表明根據ATP-X歷史故障數據，可短期預測未來59 d該設備的故障率變化趨勢。這為全路備品備件的充分儲備和電務資源的合理調配提供了參考依據。

4 預測結果分析

為了說明混沌預測ATP設備故障率變化趨勢的有效性，本文將混沌預測結果和直接進行SVR預測的結果做比較。兩者最主要的區別是：混沌預測是將相空間重構之后得到的矩陣Y作為輸入，而SVR預測是直接將ATP百萬公里故障率時間序列X作為輸入；前者處理的對象是相點，后者則是序列的元素。

按照前節的描述，以ATP-X的百萬公里故障率時間序列X作為輸入，取ε=0.01，選擇最佳參數c=1,g=0.001 700 3(相應地，最小的MSE=0.004 009 4)，得到得到圖10所示的預測結果。

圖9和圖10所示的預測結果優劣很難定性比較，于是，分別求取兩者預測的平均平方誤差和平方相關系數，結果見表1。

表1 混沌預測和SVR預測結果比較

由表1可得，對于同一個ATP-X的百萬公里故障率時間序列，混沌預測的平均平方誤差小于SVR預測的平均平方誤差，且前者的平方相關系數大于后者的平方相關系數。表明混沌預測的精度高于SVR的預測精度。

此結論也可通過圖11所示兩者預測的相對誤差圖 ((預測值-原始值)/原始值)反映，混沌預測的相對誤差相對于SVR預測的誤差，更集中于區間[-0.01,0.01]。

綜上，基于混沌理論對ATP車載設備故障率變化趨勢的預測相對更適合、更準確。

5 結論

ATP車載設備百萬公里故障率時間序列具有最大Lyapunov指數判斷的混沌特性。基于混沌理論對ATP車載設備故障率預測方法是可行和有效的，其預測精度高于支持向量回歸方法。

預測結果可供優化未來維修周期內全路ATP備品備件的統一配置和調配方案參考。在備品備件細化分類的數據基礎上，本方法可針對某種特定的備件做專項預測，提供該備件合理的儲備數量及維修策略。

參考文獻：

[1] 魏文.基于混沌和PSO神經網絡的短時交通流預測研究[D].成都:西南交通大學,2010:29-52.

[2] 吳華穩，王富章. 基于最大Lyapunov指數的鐵路貨物運量預測研究[J].鐵道學報,2014,36(4)：8-13.

WU Huawen, WANG Fuzhang. Research on Railway Freight Traffic Prediction Based on Maximum Lyapunov Exponent[J]. Journal of the China Railway Society, 2014, 36(4): 8-13.

[3] 朱子虎，翁振松. 基于混沌理論的鐵路客貨運量預測研究[J].鐵道學報,2011,33(6):1-7.

ZHU Zihu, WENG Zhensong. Railway Passenger and Freight Volume Forecasting Based on Chaos Theory[J]. Journal of the China Railway Society, 2011, 33(6): 1-7.

[4] 張洪賓，孫小端，賀玉龍. 短時交通流復雜動力學特性分析及預測[J].物理學報,2014,63(4)：1-8.

ZHANG Hongbin, SUN Xiaoduan, HE Yulong.Analysis and Prediction of Complex Dynamical Characteristics of Short-term Traffic Flow[J]. Acta Physica Sinica,2014, 63(4):1-8.

[5] 張玉梅，吳曉軍，白樹林. 交通流量序列混沌特性分析及DFPSOVF預測模型[J].物理學報，2013，62(19)：1-9.

ZHANG Yumei, WU Xiaojun, BAI Shulin. Chaotic Characteristic Analysis for Traffic Flow Series and DFPSOVF Prediction Model[J]. Acta Physica Sinica,2013, 62(19):1-9.

[6] 馬軍海，齊二石，莫馨. 混沌時序重構及上海股票指數預測的應用研究[J].系統工程理論與實踐， 2003，23(12)：86-93.

MA Junhai, QI Ershi, MO Xin. Application Study on Reconstruction of Chaotic Time Series and Prediction of Shanghai Stock Index[J]. Systems Engineering-Theory & Practice,2003, 23(12):86-93.

[7] 高俊杰.混沌時間序列預測研究及應用[D].上海:上海交通大學,2013:36-70.

[8] 韓敏.混沌時間序列預測理論與方法[M].北京:中國水利水電出版社,2007:10-240.

[9] 孟洋洋，盧繼平，王堅. 基于Volterra自適應濾波器的風電功率混沌預測[J].電力系統保護與控制， 2012,40(4)：90-95.

MENG Yangyang, LU Jiping, WANG Jian. Wind Power Chaos Prediction Based on Volterra Adaptive Filter[J]. Power System Protection and Control,2012, 40(4):90-95.

[10] 張勇，關偉. 基于最大Lyapunov指數的多變量混沌時間序列預測[J].物理學報,2009,58(2)：756-763.

ZHANG Yong, GUAN Wei. Predication of Multivariable Chaotic Time Series Based on Maximal Lyapunov Exponent[J]. Acta Physica Sinica,2009, 58(2): 756-763.

[11] 傅貴，韓國強，逯峰，等. 基于支持向量機回歸的短時交通流預測模型[J].華南理工大學學報:自然科學版,2013,41(9):71-76.

FU Gui, HAN Guoqiang, LU Feng, et al. Short-term Traffic Flow Forecasting Model Based on Support Vector Machine Regression[J].Journal of South China University of Technology:Natural Science Edition,2013, 41(9): 71-76.

[12] 曹善成，宋筆鋒，殷之平，等. 基于支持向量機回歸的飛行載荷參數識別研究[J].西北工業大學學報， 2013,31(4):535-539.

CAO Shancheng, SONG Bifeng, YIN Zhiping, et al. Establishing a Flight Load Parameter Identification Model with Support Vector Machine Regression[J]. Journal of Northwestern Polytechnical University, 2013,31(4) :535-539.

[13] 王小川，史峰，郁磊.MATLAB神經網絡43個案例分析[M].北京：北京航空航天大學出版社,2013：114-152.