基于數學形態學濾波的電壓暫降檢測方法

康軍勝，劉桂英，廖耀華，李 琳，范 豐（長沙理工大學電氣與信息工程學院，湖南長沙410114）

?

基于數學形態學濾波的電壓暫降檢測方法

康軍勝，劉桂英，廖耀華，李 琳，范 豐
（長沙理工大學電氣與信息工程學院，湖南長沙410114）

摘要：針對動態電壓恢復器對電壓暫降特征量檢測的實時性和準確性要求，與移相小角度的αβ－dq變換相結合，提出了一種使用雙結構數學形態學濾波的快速電壓暫降檢測方法。即將構造出的雙結構數學形態學濾波器對電網單相電壓中的諧波、噪聲等干擾進行預處理后，將待測單相電壓移相一個小角度形成相互垂直且正交的αβ兩相電壓，再采用αβ－dq變換并用數學形態學濾波器代替傳統的二階巴特沃斯低通濾波器實現對非直流量的濾波，實現實時、準確地檢測電壓暫降發生的起止時間、暫降幅值和相角變化；為避免鎖相過程產生的延時和輸出誤差，用基波特征參考值代替鎖相環節；該方法原理清晰、計算簡單。仿真實驗結果表明該方法具有抗干擾、延時小、檢測結果準確性高的優點。

關鍵詞：電壓暫降；形態學濾波；移相小角度；αβ－dq變換；仿真

0 引言

隨著精密用電設備的廣泛使用及其對電能質量的要求不斷提高［1］，電能質量擾動對用戶的影響也日益增大。動態電壓恢復器（Dynamic Volt?age Restorer，DVR）是一種可靠保證敏感負荷的供電電壓在受到系統電壓擾動時仍處于安全工作范圍的串聯型補償裝置。實現電壓暫降的分析和檢測，對于研究相應的預防和保護措施具有重要的意義［2］，也是實現電壓暫降動態補償的關鍵。

由于配網系統中電網電壓暫降大多由電網單相故障引起，實現對單相電壓暫降的檢測并實施有效治理措施己引起了國內外的廣泛關注［3］。單相系統中需要構造出虛擬的三相系統，才能運用d?q變換。單相系統構造出相互垂直且正交的兩相電壓，才能通過αβ?dq變換進行檢測。

文獻［4］利用單相電壓延遲60°構造虛擬的三相系統和文獻［5］根據實測的單相電壓延時90°來構造靜止坐標系中的α、β分量是兩種用移相構造對單相電壓暫降進行檢測的方法，該方法檢測實時性差。雖然文獻［6］利用求導的方法將單相電壓由αβ靜止坐標系轉換到d?q旋轉坐標系，使得檢測計算量減少，但仍沒有克服求導法本身的缺陷；文獻［7］提出的改進算法是在αβ?dq變換檢測法的基礎上，利用單相電壓移相一個可調的角度構造出相互垂直且正交的兩相電壓。該方法雖然計算簡單，但由于使用鎖相環（PLL）和電網中諧波、噪聲等干擾的存在，使用傳統的巴特沃斯低通濾波器已滿足不了動態電壓恢復器中對電壓暫降檢測的實時性和準確性要求。

本文根據數學形態學濾波和移相小角度電壓暫降檢測方法的基礎上，提出了一種使用雙結構數學形態學濾波的快速電壓暫降檢測方法。即利用構造出的雙結構數學形態學濾波器具有的良好非線性低通濾波特性，對電網單相電壓中的諧波、噪聲等干擾進行預處理后，將待測單相電壓進行移相小角度的αβ?dq變換并用數學形態學濾波器代替傳統的二階巴特沃斯低通濾波器實現對非直流量的濾波，實現實時、準確地檢測出電壓暫降發生的起止時間、暫降幅值和相角變化。所用到的基波特征參考值實時得到，取代了鎖相環節。該方法原理清晰、計算簡單，避免了傳統檢測方法的缺點。仿真結果表明該方法具有抗干擾能力強、檢測延時小、檢測結果準確性高的特點。

1 延時小角度電壓暫降檢測方法

由單相電壓通過移相來構造αβ坐標系中的uα、uβ分量，具體過程如下：如圖1所示，令待測量u1等于矢量uβ即uβ＝u1＝Usin（ωt＋δ），uδ由uβ移相角度δ得到；uδ幅值同樣為U；由uδ端點向uα作垂線交uα反向延長線于一點，得到與uβ方向相反的矢量u01和與uα方向相反的矢量u02。

圖1　移相角度δ構造αβ量矢量圖

顯然矢量u01的幅值為Ucosδ，即：u01＝－uβcosδ。

矢量u02的幅值為Usinδ，即：u02＝－uαUsinδ。

又可知，矢量u02＝u01＋uδ，即

－uαsinδ＝uδ－u01cosδ

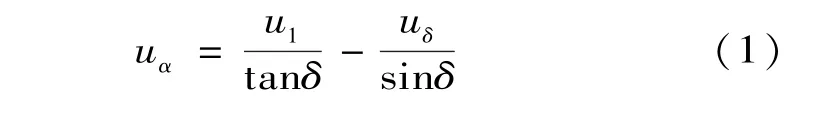
化簡得到式中：δ為可移相的角度。

圖2中uα＝Ucos（ωt＋δ）和uβ＝Usin（ωt ＋δ）分別為電壓矢量在αβ靜止坐標系兩個坐標軸上的投影。由原理知電壓矢量與d?q旋轉坐標系同步旋轉，d?q旋轉坐標系相對于靜止坐標系以角速度ω旋轉。其中ud＝Ucosδ和uq＝Usinδ由電壓矢量在d?q旋轉坐標系的投影得到。由以上分析可知uα和uβ變換到d?q坐標系的算法如下：

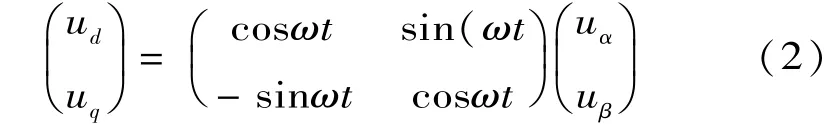
假設每個工頻周期采樣點數為N，移相角δ可以選取為360 k／N（k為正整數）。uδ由當前采樣點之前的第k點得到。當k很小時，檢測結果與用差分求導法的檢測結果近似等效。

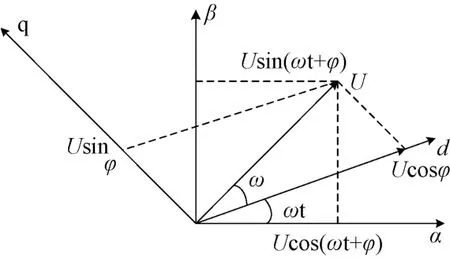
圖2　αβ坐標系變換d?q坐標系

將式（1）代入式（2）進一步推導，可得

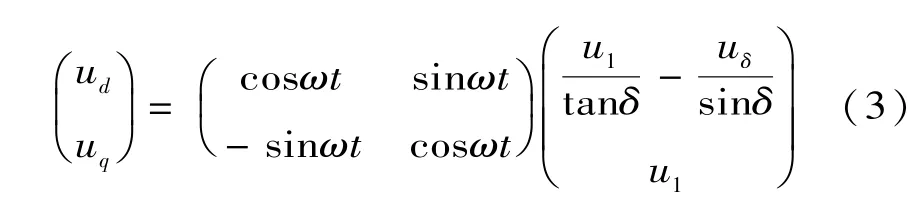
當信號中含有諧波時，設

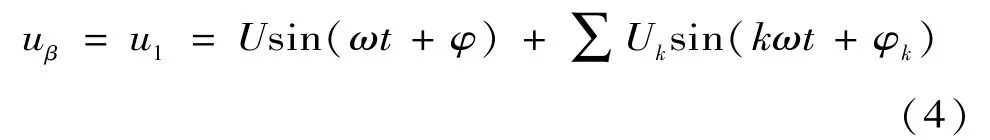
則

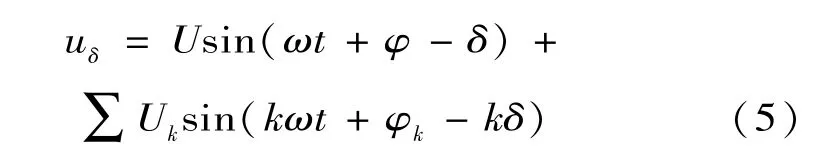
將式（4）、式（5）代入式（3），運算可得

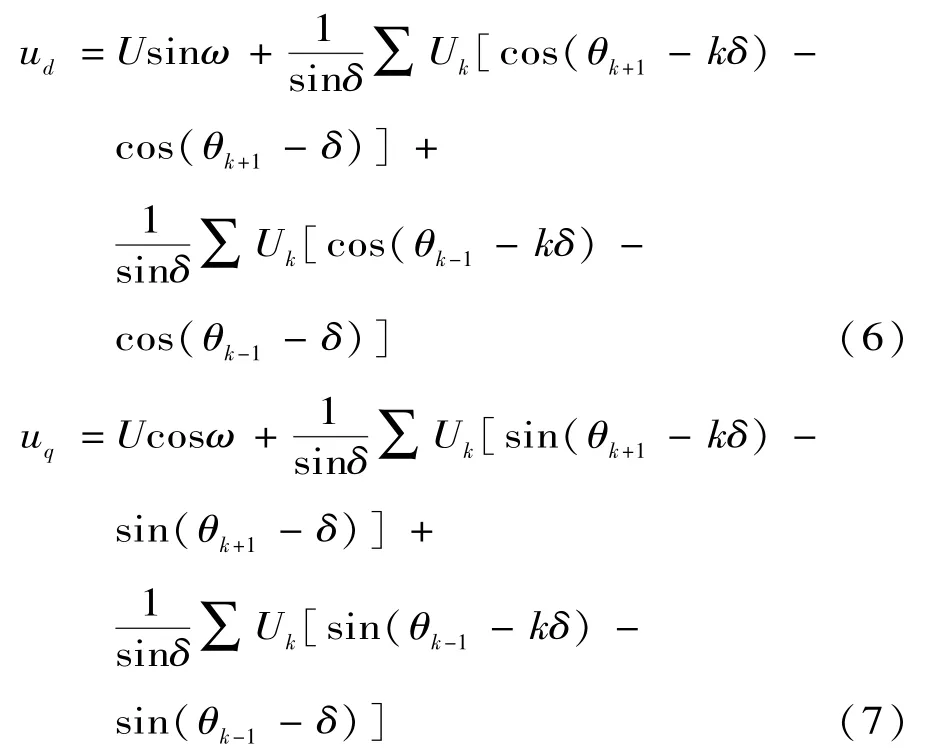
式中：θk＋1＝（k＋1）ωt＋φk，θk－1＝（k－1）ωt＋φk。用低通濾波器進行濾波可得到直流分量ud0和uq0，則基波電壓的幅值和相位跳變分別為

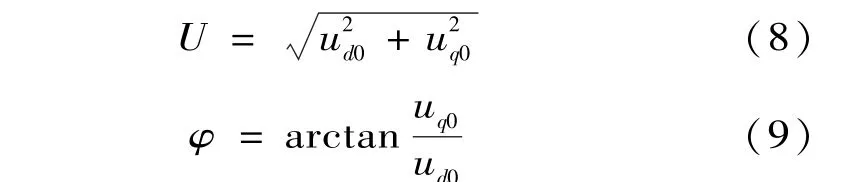
由式（6）、式（7）可知，電壓基波在運算結果中表現為直流分量，第k次高頻振蕩信號被分解成k±1次高頻振蕩信號的疊加。

綜上分析及文獻［7］的仿真結果可知，當移相角δ較小時，檢測延時小，對信號中的擾動分量有較大的放大作用；當移相角δ較大時，減小對擾動的放大作用，檢測延時隨之增大［7］。為增加抗干擾能力、減小檢測延時、提高檢測精確性，需要新型的濾波器與該方法配合使用。

2 新型數學形態學濾波的實現

2. 1 數學形態學濾波的基本原理

數學形態學濾波是在數學形態學［8］的基礎上，利用預先設定好的結構元素對信號進行形態學處理和分析來提取出有用信息，以達到噪聲抑制的目的。與傳統的低通濾波器相比，主要是由布爾運算和少量加法運算組成的形態學濾波器具有運算簡單且延時短的優點［9］。利用腐蝕來定義開運算、膨脹來定義閉運算。

設采樣一維多值信號得到輸入序列f（n），定義域為D（f）＝｛0，1，2，…，N－1｝，預設的一維結構元素序列為g（x），定義域為D（g）＝｛0，1，2，…，M－1｝；其中M和N為N≥M的整數。則膨脹和腐蝕運算分別定義為

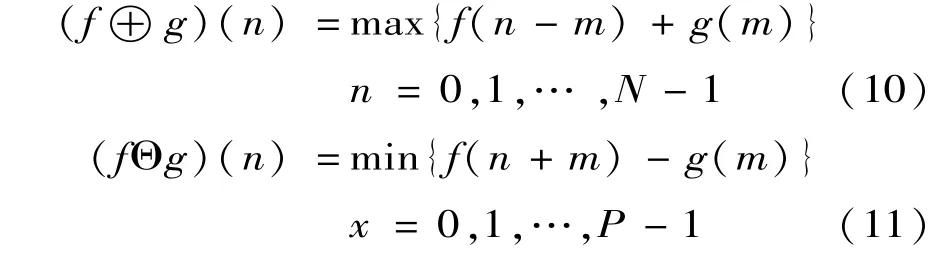
式中：⊕為膨脹運算；Θ為腐蝕運算。

由式（10）和式（11）可得到形態學開、閉運算定義分別為

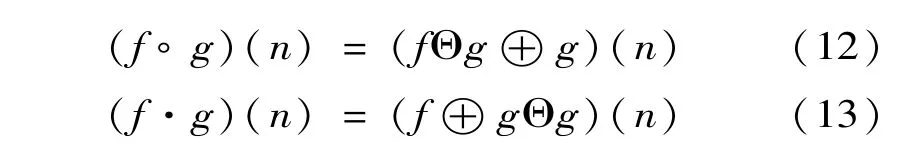
式中：?為開運算；·為閉運算。

基于開、閉運算可以構建以下3種濾波算法：交替濾波器

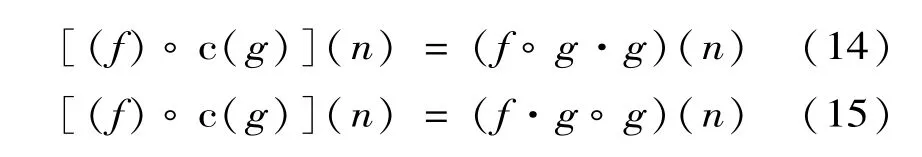
混合濾波器

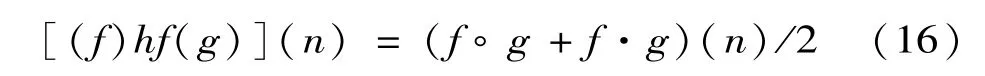
交替混合濾波器

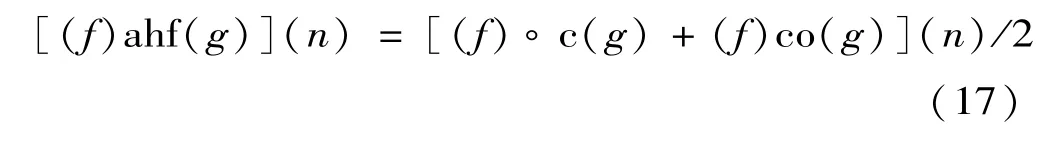
2. 2 構造雙結構數學形態學濾波器

形態學濾波器的濾波效果不僅依賴于濾波器的變換形式、結構元素的形狀和長度，為有效濾波還需結構元素的形狀、長度匹配所要濾除的信號。其中結構元素形狀的選取最為關鍵。

常用結構元素的形狀有余弦、半圓、三角、直線等［10］。文獻［11］根據電力系統數據采集中常見的噪聲干擾，將幾種常用結構元素的濾波特性進行了詳細的仿真對比。余弦結構元素具有濾波效果好、運算速度快的優勢，在處理高頻連續干擾、隨機背景噪聲時，可優先考慮使用。半圓結構在處理脈沖噪聲干擾時不僅在濾波上有很好效果，也有較快的計算速度。直線結構元素對直流偏移量干擾，有提取作用。由于電網電壓中多樣性的噪聲干擾和對濾波速度的要求，為更好的發揮各結構元素的濾波優勢，本文采用余弦型結構和半圓型結構的雙結構元素組成的交替混合濾波器。其基本形式如圖3所示。

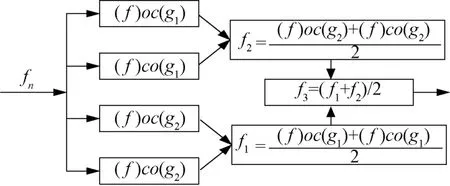
圖3　雙結構交替混合濾波器

其中，g1表示為余弦結構元素；g2表示為半圓結構元素；輸入信號通過交替混合濾波器的輸出分別為f1、f2。

2. 3 基波特征參考值的計算方法

根據文獻［9］中原理，可將實時得到的基波特征參考值取代傳統方法中的鎖相環，避免輸出誤差和鎖相延時。為此正確得到式（3）中的sinωt和cosωt極為關鍵。電壓暫降會引起系統電壓的畸變，采用如圖4所示方法可得到穩定正弦正交的參考值［12］。

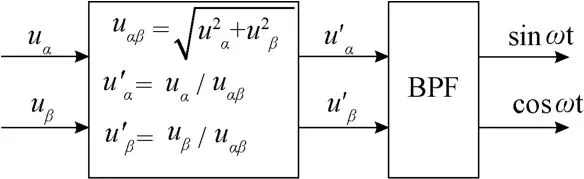
圖4　基波特征參考值的形成

單相電壓變換后得到正交電壓uα和uβ。由于電壓發生暫降時，uα不再正交于uβ，經過圖4的變換后，可得到正交的參考電壓。由于得到不一定為正弦量的u’α和u’β，故需要通過帶通濾波器才能得到相應的基波特征參考值，即sinωt和－cosωt。

2. 4 新型電壓暫降檢測方法

基于數學形態學濾波的電壓暫降檢測方法的實現可用流程圖如圖5所示。

圖5　新檢測方法流程圖

u0為實測的電網單相電壓矢量，使用本文提出的雙結構形態學濾波器對實測的單相電壓中所含有多種形式的噪聲干擾和諧波進行濾波預處理。經移相小角度的αβ?dq變換后所獲得的直流分量中仍會含有少量的噪聲干擾。直線型結構元素的特點是可以濾除直流分量中的各次諧波，濾波精確度高，實時性好［13］。此時選用單結構元素的直線型形態濾波器代替二階巴特沃斯低通濾波器進行低通濾波，從而快速、精確的得到電壓暫降的三個特征量。

3 系統仿真分析

利用Matlab／Simulink仿真軟件對單相電壓發生的電壓暫降事件進行仿真比較分析，發生暫降的相電壓幅值為220 V、基波頻率為50 Hz。

DVR裝置主電路拓撲結構為公用直流母線的三單相橋結構［14］，各相可獨立進行補償，互不影響；逆變器直流側儲能裝置為電容器。本文提出的單相檢測方法可很好應用于上述結構。

設定在時間0. 087～0. 163 s幅值暫降50%，0. 16 s相位跳變30°，含有的諧波情況與文獻［7］中相同，即幅值為12 V、10 V、9 V、8 V的5、7、11、13次諧波，并有白噪聲和脈沖噪聲干擾。加入功率為0. 02 dBW的白噪聲干擾，在0. 088 s和0. 164 s加入幅值為110 V的脈沖噪聲干擾。

3. 1 單相電壓原始波形預處理

仿真對比中，電壓采樣頻率為10 kHz，二階巴特沃斯低通濾波器的截止頻率180 Hz，就濾波效果、運算速度的比較衡量來進行結構元素選取，本文濾波器選取余弦結構幅值為基波幅值的0. 5，元素長度為26，半圓結構幅值為基波幅值的0. 8，元素長度為60。對單相電壓原始波形進行濾波的效果如圖6所示，其中圖6（a）為待測單相電壓的原始波形，圖6（b）為采用2階Butterworth濾波器處理后的波形，圖6（c）為本文濾波器濾波效果。

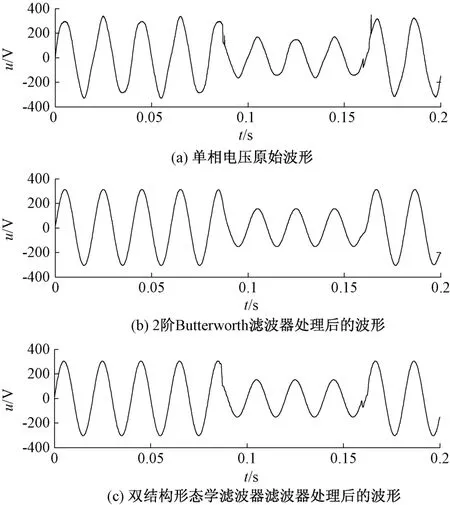
圖6　兩種濾波器的濾波效果對比

單相電壓原始波形信噪比為25. 337 41dBW。通過對比圖6中的濾波效果可知，使用二階巴特沃斯低通濾波器和雙結構的形態學濾波器濾波處理后波形的信噪比分別為26. 043 7 dBW和28. 834 3 dBW，兩種濾波器都能濾除白噪聲和脈沖噪聲，前者造成的波形失真較大，并有相位延遲；后者還較好保留了原信號的基波特征，說明所提出的雙結構形態學濾波器較為理想。

3. 2 單相電壓暫降檢測方法比較

用構造出的雙結構數學形態學濾波器對含有5、7、11、13次諧波及噪聲的電網單相電壓進行預處理，將處理后的單相電壓進行移相角δ為11. 25°的αβ?dq變換。由式（6）、式（7）可知，除了得到直流分量外還主要含有4、6、10、12次諧波，為準確地檢測電壓暫降發生的起止時間、暫降幅值和相角變化，用直線型結構元素形態學濾波器代替傳統的二階巴特沃斯低通濾波器對dq變換結果進行低通濾波。

直線結構元素的形態濾波器濾波效果由結構元素的寬度決定，綜合考慮濾波效果和動態響應時間，結構元素的寬度選取為51。為驗證本文方法的有效性，將本文方法與文獻［6］中方法進行對比，得到圖7的結果。

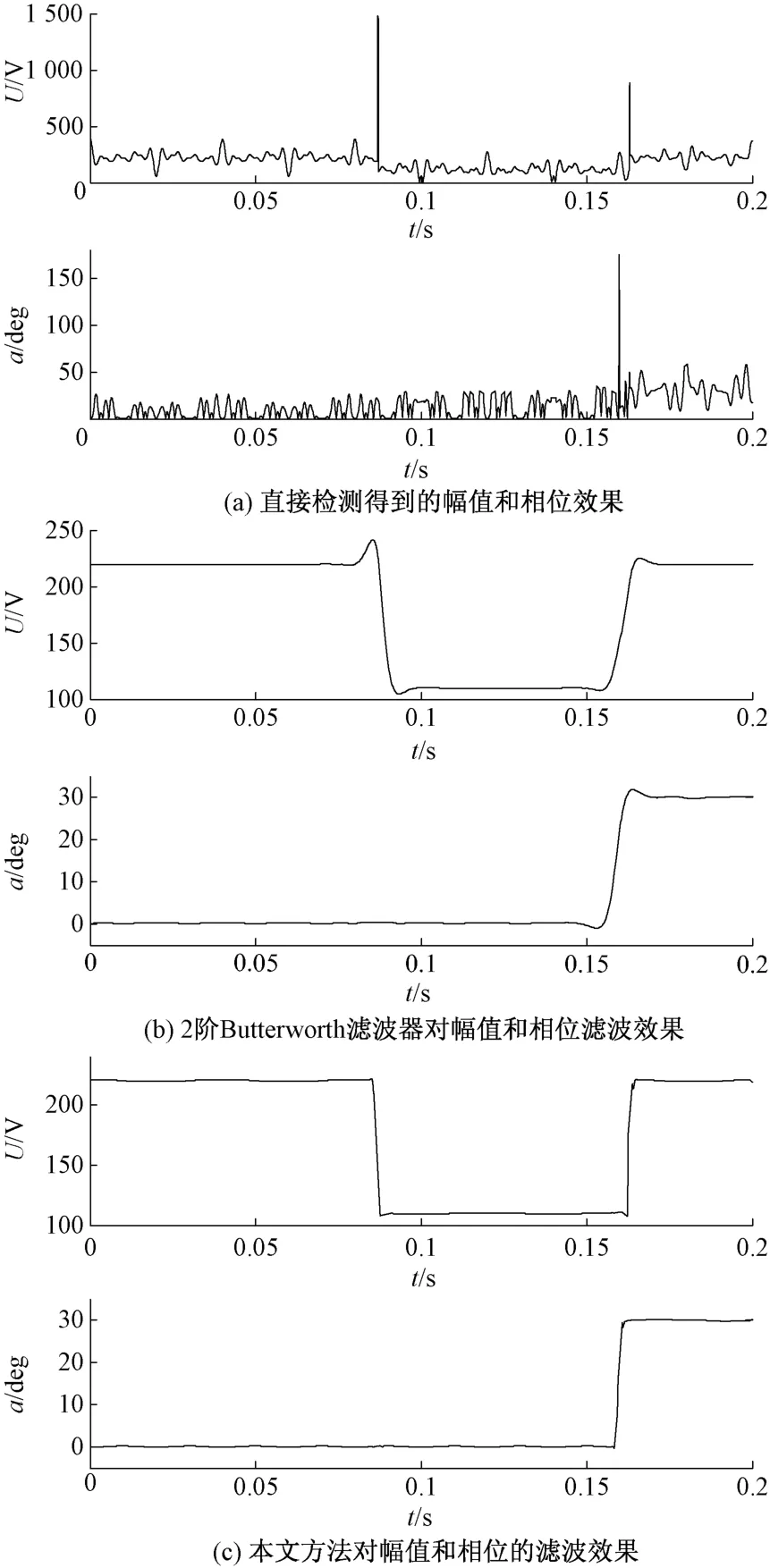
圖7　兩種濾波器對幅值和相位的濾波效果對比

由于檢測方法本身對擾動的放大作用，使得在暫降檢測的起止時刻均會出現“毛刺”現象，這會對DVR裝置的補償效果造成影響。由圖7 （a）可知，直接對原信號進行檢測，結果中得到的“毛刺”相當大，影響了檢測結果的正確性。由圖7（b）可知，傳統的二階巴特沃斯低通濾波器不能將“毛刺”有效濾除，影響檢測的準確度，不僅給系統帶來10 ms以上的濾波延時，濾波結果中還含有部分諧波，當諧波含量更高時，還會帶來更大的濾波延時。由圖7（c）可知，使用直線型結構元素形態學濾波器明顯減小了“毛刺”現象，造成的系統延時大概1 ms，具有較好較快的濾波效果，不僅提高了系統的抗干擾能力，同時可以適當減小移相角從而提高檢測的快速性。不過波形中仍含有少量低次諧波。提高直線型結構元素形態學濾波器的截止頻率雖然會減小濾波延時，同時也會降低檢測的準確度。基于數學形態學濾波的電壓暫降檢測方法已很好滿足動態電壓恢復器對電壓暫降特征量檢測的實時性和準確性要求。

4 結論

本文根據數學形態學濾波和移相小角度電壓暫降檢測方法的基礎上，提出了一種使用雙結構數學形態學濾波的快速電壓暫降檢測方法。即利用構造出的雙結構數學形態學濾波器具有的良好非線性低通濾波特性，對電網單相電壓中的諧波、噪聲等干擾進行預處理后，將待測單相電壓進行移相小角度的αβ?dq變換并用數學形態學濾波器代替傳統的二階巴特沃斯低通濾波器實現對非直流量的濾波，很好協調了檢測的實時性與精確性之間的對立關系。實現實時、準確地檢測電壓暫降發生的起止時間、暫降幅值和相角變化。所用到的基波特征參考值實時得到，取代了鎖相環節。該方法原理清晰、計算簡單，避免了傳統檢測方法的缺點。仿真對比試驗的結果表明該方法具有抗干擾能力強、檢測延時小、檢測結果準確性高，滿足實時性和準確性的要求。

參考文獻：

［1］李燕楠，包廣清．基于小波包和支持向量機的電能質量擾動識別［J］．電力科學與工程，2012，28（3）：21－26．

［2］肖助力，龔仁喜，陳雙．一種改進不完全S變換的電壓暫降檢測方法［J］．電力系統保護與控制，2015，（9）：62－68．

［3］潘進賢，邵振國．基于直覺模糊集熵測度的電壓暫降源定位方法［J］．電力科學與工程，2015，31（1）：38－43．

［4］肖湘寧，徐永海，劉連光．考慮相位跳變的電壓凹陷動態補償控制器研究［J］．中國電機工程學報，2004，22（1）：64－69．

［5］楊亞飛，顏湘武，婁堯林．一種新的電壓驟降特征量檢測方法［J］．電力系統自動化，2004，28（2）：41 －44．

［6］張慶超，肖玉龍．一種改進的電壓暫降檢測方法［J］．電工技術學報，2006，21（2）：123－126．

［7］瞿碩，黃純，江亞群，等．DVR電壓暫降檢測新方法［J］．電工技術學報，2013，28（4）：234－239．

［8］陳平，李慶民．基于數學形態學的數字濾波器設計與分析［J］．中國電機工程學報，2005，25（11）：60－65．

［9］丁寧，徐永海，肖湘寧．基于p－q－r變換和數學形態濾波的電壓暫降檢測算法［J］．電力自動化設備，2011，31（3）：89－93．

［10］黃耀東，張穎，韓子騫．基于數學形態濾波的電壓閃變檢測研究［J］．電力科學與工程，2014，30（8）：69－73．

［11］趙昭，劉利林，張承學，等．形態學濾波器結構元素選取原則研究與分析［J］．電力系統保護與控制，2009，（14）：21－25，35．

［12］譚智力，李勛，陳堅，等．基于簡化p－q－r理論的統一電能質量調節器控制策略［J］．中國電機工程學報，2008，27（36）：85－91．

［13］崔紅芬，李鵬，王暢．基于數學形態學的微網電壓補償量檢測方法［J］．中國電機工程報，2013，33 （16）：122－128．

［14］王同勛，薛禹勝，CHOI S S．動態電壓恢復器研究綜述［J］．電力系統自動化，2007，31（9）：101－107．

Voltage Sag Detection Based on Mathematical Morphology Filtering Method

KANG Junsheng，LIU Guiying，LIAO Yaohua，LI Lin，FAN Feng
（College of Electrical and Information Engineering，Changsha University of Science＆Technology，Changsha 410114，China）

Abstract：A method using a double structure of mathematical morphology filter for fast voltage sag detection is pro?posed in this paper to meet the requirements of both real time property and accuracy for the voltage sag detection characteristics of the dynamic voltage restorer，which combines a small angle shifting in phase with αβ?dq trans?form．After being pretreated by the constructed double structure mathematical morphology filter，the single?phase voltage containing harmonics and noises shifted in phase with a little angle and then become two perpendicular and orthogonal αβ phase voltage．And then the αβ?dq transform is conducted and mathematical morphology filter is uti?lized to replace the traditional second?order butterworth low?pass filter to smooth the straight flow．By this method，the real?time and accurate detection of voltage sag start?stop time and temporary decline in value and phase angle change can be realized．To avoid delay and output error produced during lock process，the fundamental characteris?tics of the reference value are used to take place of the phase?locked loop section．The principle of the method is concise and simple．The advantages of anti?interference，small time delay and good accuracy of the method are demonstrated by the simulation results and tests．

Keywords：voltage sag；morphologic filter；phase?shifting angle；αβ?dq transform；simulation

作者簡介：康軍勝（1990－），男，碩士研究生，研究方向為電力系統運行與控制、電能質量監控等，E?mail：k＿junsheng ＠163. com。

收稿日期：2015－09－20。

中圖分類號：TM73

文獻標識碼：A

DOI：10. 3969／j. issn. 1672-0792. 2016. 01. 012