利用CORDIC算法提取脈內特征在FPGA上的實現
王煒珽 張文旭 陶東香


摘 要: 介紹了坐標旋轉數字計算(CORDIC)算法的原理,給出了利用CORDIC算法提取信號脈內特征的迭代公式,在此基礎上實現了用該算法的流水型迭代結構提取瞬時幅度、相位和頻率的FPGA電路,解決了電路中的時鐘與寄存器配置、數據的補碼格式和相位累加等問題。通過在硬件芯片上的下載驗證,表明電路結構合理、測試有效,滿足設計要求。
關鍵詞: 坐標旋轉數字計算; 脈內特征; FPGA設計; 補碼
中圖分類號: TN79?34 文獻標識碼: A 文章編號: 1004?373X(2016)09?0001?05
Abstract:The principle of the coordinated rotation digital computer (CORDIC) algorithm is introduced. The iterative formula of the signal in?pulse characteristics extracted by CORDIC algorithm is proposed. On this basis, the FPGA circuit of extracting the instantaneous amplitude, phase and frequency by pipeline iterative structure of the algorithm was realized. The problems of clock and register configuration, data′s complementary code format and phase accumulation in the circuit were solved. The downloading verification on hardware chip shows that the circuit structure is reasonable, and test is effective. The circuit can satisfy the design requirement.
Keywords: coordinated rotation digital computor; in?pulse characteristics; FPGA design; complementary code
0 引 言
現代電子戰中,提取輻射源信號脈內特征已成為許多電子偵查設備必備的功能,在此,僅以針對輻射源的測向技術為例,如比幅法需要知道脈沖的幅度信息、干涉儀法需要知道高精度的脈內瞬時相位和頻率等。坐標旋轉數字計算(Coordinated Rotation Digital Computer,CORDIC)算法是各種用來提取脈內特征的方法中較為常見的一種。該算法最早由J.Volder等人在1959年提出[1],最初用它進行坐標變換。其基本思想是通過多次的迭代實現方向反復搖擺、數值逐次遞減以逼近最終需要到達的角度,同時計算出與該角度有關的某些復雜函數運算結果。統一的CORDIC算法由J.S.Walther在1971年提出[2],他將圓周、線性、雙曲線三種算法和旋轉、矢量兩種模式統一到一個迭代方程中,為實現多模式共存的CORDIC算法硬件結構奠定了理論基礎。CORDIC因能通過簡單的移位和加減操作就能實現乘除、開方、三角變換、對數、指數等原本需要大量乘法器的運算,所以非常適合用FPGA設計實現[3?5]。
本文在分析圓周CORDIC算法原理的基礎上,給出了利用CORDIC算法提取信號脈內特征的迭代公式,實現了用該算法的流水型迭代結構提取瞬時幅度、相位和頻率的FPGA電路,在電路的設計過程中解決了電路中的時鐘與寄存器配置、數據的補碼格式和相位累加等問題。在信號分選、脈沖識別、輻射源定位等技術領域有一定的實用價值。
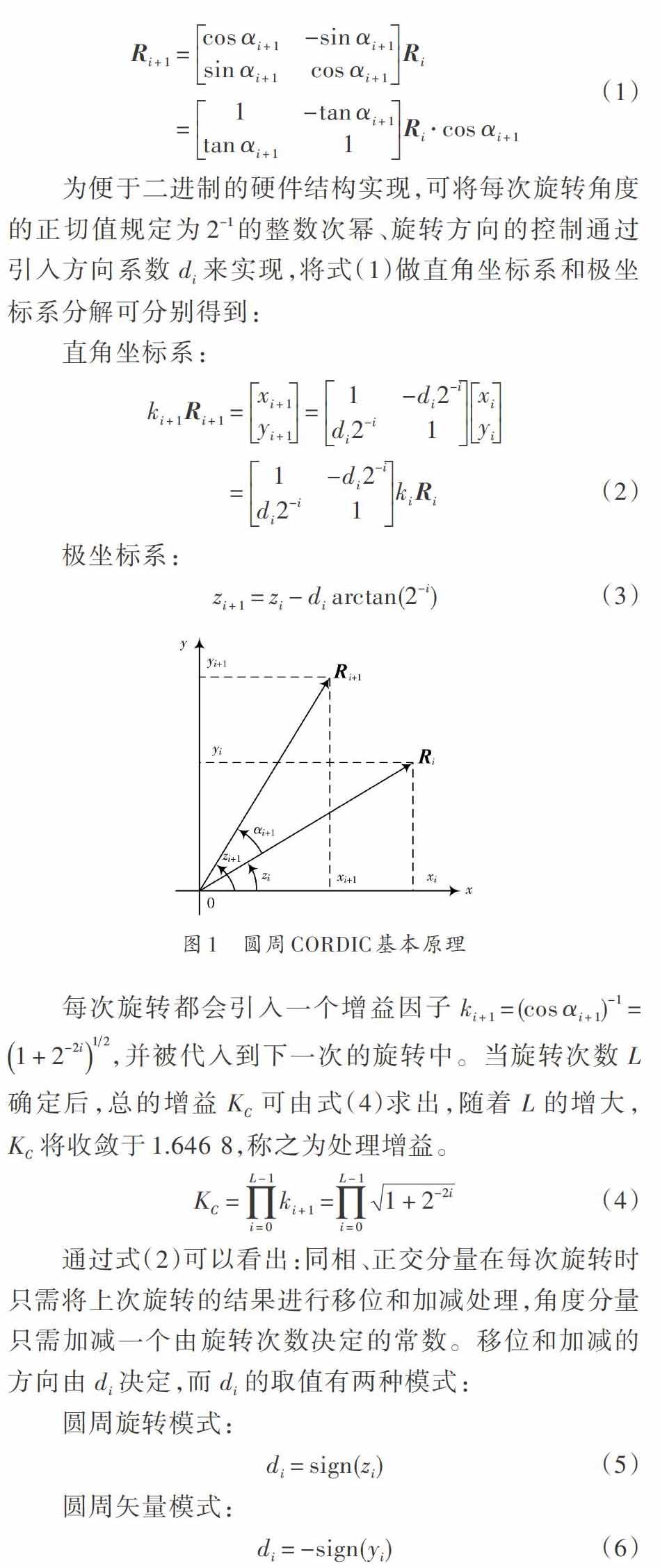
1 圓周CORDIC算法原理
兩種方法的主要區別在于:前者計算的瞬時頻率仍在[-π,π]之間,但要加入判斷電路;而后者的計算結果在[0,2π]之間,但在硬件電路中實現取模運算非常簡單,有時甚至都不需要運算。由于圓周矢量模式CORDIC算法是對同相正交分量的計算,因此檢測輸出的頻率可能出現負頻率。這在硬件電路中用補碼表示負數的方法即可解決,因為正余弦函數的周期對稱特性使弧度在[0,2π]之間的取值本身就是其在[-π,π]之間取值的補碼形式。分別利用式(9)和式(10)對2.1節仿真得到的瞬時相位求瞬時角頻率,Matlab仿真結果如圖3所示,其中圖3(a)是存在相位卷繞的結果,圖3(b)是用第二種方法解相位卷繞并將補碼換算為正常負數的結果。從圖3可見仿真結果正確地檢測出了瞬時角頻率,且符合上行LFM規律。
3 流水型CORDIC電路在FPGA上的實現
3.1 CORDIC算法迭代結構分析
CORDIC算法原理簡單且易于理解和仿真,其難點在于如何設計合理的迭代結構來實現運算過程。迭代類算法通常有兩種結構實現,即循環反饋型迭代結構(簡稱循環結構)和流水型迭代結構(流水結構)。循環結構是指通過單級算法單元實現多次迭代計算,將每次的計算結果反饋回本級進行下一次計算,如此循環[L]次以得到最終結果。流水結構是指通過多級算法單元實現多次迭代計算,將每級的計算結果輸入到次級進行下一次計算,經過[L]級后得到最終結果。兩種結構都必須在延遲[L]個時鐘后完成計算。循環結構的優點是相對簡單、硬件資源需求低;而流水結構恰恰相反。循環結構的缺點是每隔[L]個時鐘才能進行一次計算,其運算速率是時鐘頻率的[1L;]流水結構沒有此問題,其運算速率等于時鐘頻率。在實際應用中,應根據設計要求、結構特點,選擇適當的實現結構[4]。圓周矢量模式CORDIC算法循環迭代結構如圖4所示,其中符號“>>”表示移位。CORDIC算法的循環結構稍作改進即可作為流水結構的單級計算單元使用。
3.2 電路的具體設計
為保證提取的信號脈內特征的實時性,本文設計的CORDIC算法電路采用流水結構,設計過程中有以下三方面的技術問題需要重點解決:
(1) 時鐘與寄存器的配置問題
考慮到一個時鐘脈沖有兩個邊沿,當輸入的同相正交數據在第0個脈沖上升沿到達時,為確保數據的穩定性,可利用第0個脈沖的下降沿承接并寄存輸入數據,再到第1個脈沖上升沿到達時計算出結果并交給下一級的寄存器,此刻本級的寄存器便可準備好在第1個脈沖下降沿到達時承接新的數據。以此可實現數據的逐級流水計算,最終在延遲了[L]個脈沖上升沿后,CORDIC模塊可輸出與第0個脈沖上升沿數據對應的幅度和相位值。
由于VHDL語言規定一個寄存器只能受一個時鐘脈沖邊沿的控制,所以CORDIC模塊每級運算單元設計了兩個寄存器:一個是用來承接上級數據的流水寄存器,由下降沿控制;另一個是用來輸出加減法結果的加法寄存器,由上升沿控制。差分模塊同樣需要兩個寄存器,但他的輸入數據寄存器可用CORDIC模塊第[L]個加法輸出寄存器替代,這也使差分模塊只需CORDIC模塊后的0.5個周期就可得到瞬時頻率。各級寄存器與時鐘的配置設計思路如圖5所示。具體的實現電路中采取[L=12]的流水級,輸出的幅度和相位數據相對于輸入的同相正交數據延遲了12個時鐘周期,瞬時頻率數據則延遲了12.5個時鐘周期。
(2) 實現用補碼表示數據的問題
在大多數的A/D轉換器和處理器中,負數都是用補碼格式表示的[11]。補碼的優點是做加定點數的減法運算時方便,無論正負數都可以直接相加,由于硬件電路中數的位數通常是固定的,所以加減運算時數據溢出會被直接去掉不影響最后結果[12],這相當于做了一次求模運算。補碼在表示負數和正數時均保持了數的單調增的變化規律,因此在做移位運算時要根據正負采取不同的方式。圓周矢量模式CORDIC算法每級迭代都是驅動正交分量[yi]向0逼近,所以對于正數采取數據右移并在高位補“0”的方法,對于負數仍是數據右移但在高位補“1”。其中[yi]可能在正負之間反復搖擺,所以對其移位要有判斷程序,對[yi]正負的判斷在求[di]時已經完成,拿來直接用即可。根據式(7)可知[xi]在第1級迭代結束后就已經被限定為正數了,且移位是從第3級迭代開始的,而其[xL]輸出的是沒有正負的幅度,因此對[xi]的移位都可按照正數執行。
對于[zi]而言,輸入為0且沒有移位的操作,只是根據[yi]的正或負逐級加上或減去一個相應的無極性原碼表示的相位常數。由于弧度表示相位時本身就體現了補碼的特性,用無極性的原碼表示相位時可認為[φ(n)∈][0,2π],用補碼表示相位時可認為[φ(n)∈[-π,π]。]同理,對于差分模塊的瞬時角頻率也是如此,故無需做專門處理即可滿足式(10)的要求。
針對輸出數據的瞬時幅度采用無極性的原碼表示,其值帶有處理增益[KC,]且[KC]趨近于1.646 8,因此幅度的位數與[xi]的位數相同,本文所設計的電路不再做其他處理。
(3) 當[x0,y0]均為0時,瞬時相位的累加問題
可見,此時瞬時相位輸出了一個非0的角度。對于同相正交分量來講,[yi,xi]均為0的情況表示信號的瞬時幅度也為0,因此可引入一個幅度閾值,通過對比[xL]與閾值的大小消除該現象,同時該閾值可做噪聲抑制門限用。
3.3 設計驗證與分析
為適應更高的數據流速,實現運算速率與時鐘頻率的一致,本文針對圖5所示的流水結構設計實現了FPGA電路并在Altera公司生產的EP4CE15F17C8芯片上進行了驗證。該FPGA電路包括CORDIC和差分兩個模塊,均借助QuartusⅡ軟件和VHDL語言設計[13]。
模塊例化集成后的原理結構設計圖如圖6所示,其中CORDIC模塊由12級流水單元構成。該電路輸入端的[xi](同相分量),[yi](正交分量)和輸出端的Aout(瞬時幅度)的位寬18位,輸出端的pnout(瞬時相位)和fnout(瞬時頻率)位寬20位,時鐘clk外接100 MHz的頻率源,與時鐘異步的使能端en在高電平有效。[xi,yi,]pnout,fnout的數據格式為補碼,Aout的數據格式是無極性的原碼。
啟動編譯器,編譯成功后得到的資源需求分析如圖7所示,該電路結構占用了1 291個邏輯單元(LE),其中用到的寄存器為1 216個。
為了驗證電路效果,輸入仿真數據并利用Quartus Ⅱ自帶的嵌入式邏輯分析儀(Signal Tap Ⅱ)進行數據的實時監測和采集。Signal Tap Ⅱ能夠將測到的信號樣本暫存在EP4CE15F17C8內嵌的RAM中,然后再通過JTAG端口將樣本送回QuartusⅡ進行顯示、分析,同時還能將采集的樣本數據轉換為txt格式文件輸出,以供其他仿真軟件如Matlab進行進一步的運算分析。輸入數據如表2所示。
為了更好地觀察時鐘的上下邊沿對模塊的控制情況,利用一個數字鎖相環將時鐘倍頻到200 MHz,每個clk時鐘周期內包含2個樣本采集點。啟動Signal Tap Ⅱ,測試得到的波形效果如圖8所示。圖8中多位數據除Aout采用“Unsigned Line Chart”格式顯示外,其他均采用“Signed Line Chart”格式顯示。從波形效果上看,按表中數據依次循環的輸入正交同相分量時,電路輸出了瞬時的幅度、相位和頻率。調幅信號的瞬時幅度為一頻率較低的正弦信號,其他兩種的瞬時幅度為一矩形脈沖信號。線性調頻信號的瞬時相位、頻率很好地體現了上行LFM的特點。從圖8中還可以看出從同相正交分量數據輸入到幅度、相位輸出之間間隔24個樣本采樣點,即輸出比輸入延遲了12個clk時鐘周期,但輸出與輸入數據的流速是相同的,這說明電路中實現了12級流水計算單元。
對比圖9、圖10可看出,圖10中當[xi=0]且[yi=0]時,Aout輸出為0,用其控制pnout輸出為1(用于調試測試數據,使用時可設為0或其他值,閾值的選取視擬抑制的噪聲幅度決定)。圖10中當[xi=0]且[yi=0]時,輸出補碼格式的相位值為-495 666,折算成歸一化弧度相位為-0.945 4π,這與式(12)一致。
4 結 論
本文設計的流水型結構電路實現了利用圓周矢量模式CORDIC算法檢測中頻脈沖信號的瞬時幅度、相位和頻率,解決了時鐘與寄存器配置、數據的補碼格式和相位累加等問題。通過在硬件芯片上的下載驗證,表明電路結構合理、測試有效,滿足設計要求。
參考文獻
[1] VOLDER J E. The CORDIC trigonometric computing technique [J]. IEEE transactions on computers, 1959, 8: 330?334.
[2] WALTHER J S. A unified algorithm for elementary function [C]// Proceedings of 1971 Spring Joint Computer Conference. [S.l.]: ACM, 1971: 379?385.
[3] 閻嘯,秦開宇,高援開,等.基于CORDIC算法的頻譜分析技術研究[J].電子科技大學學報,2006,36(3):335?338.
[4] 張俊濤,王紅倉.基于FPGA的CORDIC算法通用IP核設計[J].微計算機信息,2008,24(7):238?240.
[5] 陳婧.改進型CORDIC算法的研究與實現[J].現代電子技術,2011,34(24):165?167.
[6] 孔德元.針對正弦余弦計算的CORDIC算法優化及其FPGA實現[D].長沙:中南大學,2008.
[7] 金鋒,佘世剛,王鍇,等.基于System Generator的PM信號CORDIC算法鑒相的仿真與實現[J].現代電子技術,2013,36(5):96?98.
[8] 閆溫合,胡永輝,李瑾琳.應用于數字下變頻中CORDIC算法的FPGA實現[J].時間頻率學報,2014,37(1):34?40.
[9] 胡愛明,胡可欣.一種雷達信號類型識別方法[J].現代電子技術,2006,29(14):123?126.
[10] 張文旭.被動雷達導引頭數字信道化接收機研究及實現[D].哈爾濱:哈爾濱工程大學,2009.
[11] 維納 K 英格爾,約翰 G 普羅克斯.數字信號處理(Matlab版)[M].劉樹棠,陳志剛,譯.3版.西安:西安交通大學出版社,2013.
[12] 杜勇.數字濾波器的Matlab與FPGA實現[M].北京:電子工業出版社,2012.
[13] 陳欣波.Altera FPGA工程師成長手冊[M].北京:清華大學出版社,2012.

