基于Nelson—Siegel模型預測中債國債收益率曲線形態

郭濟敏 張嘉為

摘要：本文探討了基于Nelson-Siegel模型擬合中債國債即期收益率曲線的有效性問題，并分析了模型參數的經濟意義；通過對比多個收益率預測模型，發現基于Nelson-Siegel模型的預測效果要好于單純的隨機游走和時間序列模型。最后，本文依此方法對2016年6月至12月的中債收益率曲線形態和關鍵期限的月收益率進行了預測。

關鍵詞：Nelson-Siegel模型 國債收益率曲線 模型擬合

國債收益率曲線反映了某一時點上國債到期收益率與到期期限之間的關系，是無違約風險利率水平的集中體現，因此也是一國金融產品定價的基準。在發達金融市場，國債收益率曲線還可以作為預測未來利率、經濟增長和通脹趨勢的工具，因而有利于更好地發揮貨幣政策的調控效果。

本文采用Nelson & Siegel（1987）1（以下簡稱N-S）的參數法來擬合國內的國債收益率曲線。該方法的優點在于：參數數量少，而且每個參數都有相應的經濟含義，因此，該模型不僅使用方便，而且能夠在實際應用中發揮較好的指導作用。本文參考Diebold & Li（2006）2的研究框架，即先基于N-S法擬合收益率曲線，然后通過構建N-S模型中的參數預測模型，并在此基礎上基于N-S法預測整條收益率曲線。

目前，國內學者在對國債收益率曲線建模時，通常選取市場上各種國債的成交數據，本文則采用中債國債即期收益率曲線數據。原因如下：一是中債國債即期收益率在計算時，對市場交易數據中的噪聲進行了有效的過濾。有研究3表明其在可靠性、公允性、穩定性和精準性方面均好于實際市場交易數據；二是銀監會將中債收益率曲線作為銀行業金融機構市場風險管理及監管部門進行市場風險監管的計量參考基準，證券業協會則將中債收益率曲線和由此推算的債券估值作為證券基金投資銀行間市場債券的公允價值。

N-S模型介紹

Charles Nelson和Andrew Siegel在1987年提出用參數模型來描述即期收益率曲線的動態變化，具體函數形式如下：

（1）

其中， 表示到期時間， 均為待估參數。

（1）當t趨于無窮時， = ，故 稱為水平參數。其中， 的變動將改變收益率曲線的高度。

（2）當t趨于零時， ，則有 因此， 被稱為斜率參數。等式（1）右邊第二項中的 在t趨向于無窮時等于0，意味著第二項主要對短期限收益率產生影響，故稱其為短期因素。

（3）當t趨于零或者無窮時，等式右邊第三項中的 均等于0，這意味著 的變動對短期和長期收益率的影響較小，其主要對中期收益率產生影響，故第三項稱為中期因素。同時， 影響曲線的曲率，故稱為曲率參數。

（4） 稱為比例參數，通常先驗給定，與時間頻度有關，頻度越高， 值越小。 決定了公式（1）第三項中 ）的極值對應的到期時間，從而決定了曲線的鞍部位置，也決定了長期和短期利率隨時間變化的速度。通常來說，中期因素 在1～3年時達到最大，對應 取值在0.05～0.15之間。Diebold & Li（2006）取 ，并在30個月時，中期因素達到最大。

基于N-S模型擬合中債國債收益率曲線

（一） 的選取

考慮到參數 對擬合效果影響很大，故首先選取最優 。具體做法如下：以2002年至2015年中債國債收益率曲線日度數據為樣本；同時，考慮到我國10年以上期限國債的流動性較差，收益率曲線定價偏差較大，因此僅采用1至10年期限的國債收益率數據。 的遍歷區間取（0.005，0.15），間隔0.001，基于給定的 ，建模給出樣本區間內每日的參數 及對應的擬合值，并計算全樣本的日均絕對誤差，最終選擇使得日均絕對誤差達到最小的 作為最優值。具體結果如圖1所示，當 =0.088時，模型擬合的日均誤差達到最小，這意味著大約在21個月時，中期因素達到最大。

圖1 不同 對應的日均誤差均值

（編輯注：橫坐標為“ 的遍歷區間”，縱坐標為“日均誤差均值”）

（二）模型擬合情況

基于2006年3月至2015年各關鍵期限國債收益率的日度數據，首先，采用N-S模型逐日進行回歸，得到日度參數值 及相應的全樣本均值；然后，將參數 的歷史全樣本均值代入公式（1），得到各期限收益率的全樣本擬合值，并與全樣本實際均值進行比較。表1列示了關鍵年限國債收益率實際值和擬合值的對比結果。表中顯示，模型擬合值與歷史均值的誤差在0～6BP之間，這意味著采用N-S模型來擬合中債收益率曲線是可行的。

表 1 最優 值下國債收益率各期限實際值、擬合值及其誤差

時間（月） 12 24 36 48 60 72 84 96 108 120

實際值 2.65 2.87 3.05 3.21 3.32 3.47 3.55 3.63 3.69 3.74

模型擬合值 2.66 2.83 3.05 3.23 3.37 3.48 3.56 3.62 3.67 3.71

誤差（BP） 1.5 -4.6 -0.7 1.97 5.1 1.07 1.2 -0.9 -1.8 -2.8

（三）參數解釋力的檢驗

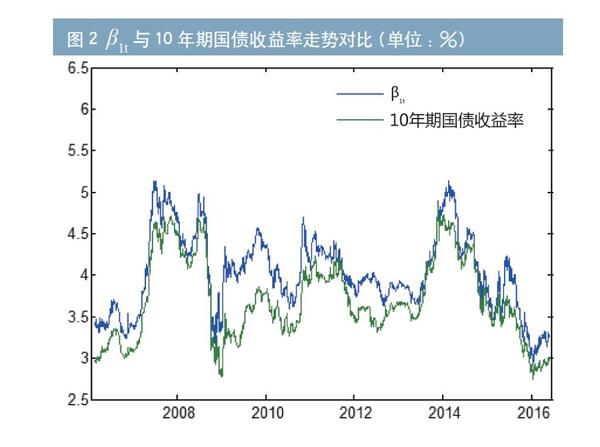
在N-S模型中， 為水平參數、 為斜率參數、 為曲率參數。本文用“10年期國債收益率”代表收益率曲線的實際水平值；“1年期國債收益率-10年期國債收益率”代表收益率曲線的實際斜率；“2×3年期國債收益率-1年期國債收益率-10年期國債收益率”代表收益率曲線的實際曲率。然后，分別計算上節擬合得到的 與曲線實際水平值、斜率、曲率的相關性，結果分別為：0.934、0.805、0.923（如圖2至圖4所示）。

圖2 與10年期國債收益率走勢對比（單位：%）

（編輯注：藍色圖例為 ，綠色圖例為“10年期國債收益率”）

圖3 與實際曲線斜率（1年期國債收益率-10年期國債收益率）對比

（編輯注：藍色圖例為 ，綠色圖例為“實際曲線斜率”）

圖4 與實際曲線曲率[2×3年期國債收益率-（1年期國債收益率+10年期國債收益率）]對比

（編輯注：藍色圖例為 ，綠色圖例為“實際曲線曲率”）

（四）模型參數與宏觀經濟指標的關系

影響債券的宏觀因素主要是兩個：經濟增長和物價。工業增加值是衡量經濟增長的高頻指標；物價則選用CPI同比增長率。這兩個指標均有月度數據可供使用。

本文將模型擬合得到的 月均值分別與CPI和工業增加值月同比增速進行當期相關和時差相關分析。結果如表2所示。

表2 模型參數與宏觀經濟指標的當期相關和時差相關關系

β1t β2t β3t

CPI 相關系數 0.41 0.32 0.35

T值（P值） 4.96（0.0000） 3.60（0.0005） 3.99（0.0001）

工業 相關系數 0.22 -0.22 -0.13

T值（P值） 2.47（0.0150） -2.47（0.0149） -1.43（0.1560）

CPI時差相關 相關系數 0.44（+3） 0.50（-5） -0.41（+10）

T值（P值） 5.28（0.0000） 6.22（0.0000） -4.841（0.0001）

工業時差相關 相關系數 0.22（0） -0.33（+7） -0.59（+10）

T值（P值） 2.47（0.0150） -3.77（0.0001） -7.87（0.0000）

注：時差相關分析中，+表示宏觀變量領先于參數，-表示宏觀變量滯后于參數。

由表2可知：（1）CPI同比增速與同期的 都是顯著正相關。但是工業增加值同比增速與同期的 不存在顯著的相關性。（2）CPI同比增速分別領先于 、 3個月和10個月，但與 是顯著正相關；與 是顯著負相關。（3）CPI同比增速滯后 5個月，并且兩者之間是顯著正相關。（4）工業增加值同比增速分別領先于 、 7個月和10個月；并且都是顯著負相關。

基于N-S模型對中債國債收益率曲線的預測

（一）預測模型的選擇

基于N-S模型預測國債收益率曲線的關鍵，是確定模型中三個參數 、 、 的月度預測模型，本文主要考慮AR和VAR預測模型。鑒于之前的研究結論顯示CPI與多個參數具有較強的相關關系，因此，本文還考慮在上述模型中加入CPI作為解釋變量。在確定參數預測模型時，為充分利用數據信息，本文采用日度數據。在選取日度收益率作為樣本時，首先擬合得到日度參數值，然后計算得到相應的月均值。至此，基于N-S的預測模型一共包括以下幾種：AR-NS，VAR-NS，AR（CPI）-NS，VAR（CPI）-NS。

構建預測模型采用的樣本期是2006年1月至2013年12月；外推預測期是2014年1月至2015年12月。外推預測采用兩種方法，一是外推1個月法；二是外推12個月法。為了更好地評價N-S模型的預測效果，本文引入隨機游走模型（模型假定本月收益率等于上月）及直接預測收益率的AR、VAR預測模型等作為對比基準模型。最終預測結果見表3和表4，表中分別列示了外推1期和外推12期的1～10年各關鍵期限月收益率預測誤差。

由表3和表4可知：（1）基于N-S的國債收益率曲線預測模型的預測效果要好于隨機游走模型和單純預測收益率的AR和VAR模型，特別是在外推12期預測中。（2）在不同預測樣本期，基于N-S的不同預測模型表現略有差異。其中，在外推12期的預測中，AR-NS模型在2014年的預測誤差最小，為17BP；VAR（CPI）-NS模型的預測誤差為18BP，與其相差不大。VAR（CPI）-NS模型則在2015年的預測誤差最小，為18BP，顯著好于其他模型；在外推1期的預測中，其與AR-NS模型預測誤差相差無幾，但在外推12期預測中，則顯著好于AR-NS模型。

在實際預測中，考慮到CPI作為外生變量本身存在的預測誤差，我們在外推1期預測中僅采用AR-NS模型；在外推12期預測中，則同時采用VAR（CPI）-NS和AR-NS兩個模型并對比各自的結果。

表3 外推1個月預測誤差

外推1月 模型 1y 2y 3y 4y 5y 6y 7y 8y 9y 10y 排名 平均誤差

隨機游走 0.22 0.19 0.17 0.14 0.13 0.15 0.14 0.15 0.14 0.14 5 0.1561

2014 AR 0.22 0.18 0.15 0.12 0.10 0.13 0.12 0.13 0.13 0.13 3 0.1408

VAR 0.26 0.23 0.20 0.18 0.15 0.17 0.15 0.15 0.16 0.15 7 0.1803

AR-NS 0.19 0.17 0.16 0.13 0.11 0.14 0.10 0.11 0.11 0.11 1 0.1324

VAR-NS 0.21 0.18 0.19 0.17 0.16 0.17 0.13 0.13 0.13 0.13 6 0.1610

AR（cpi）-NS 0.20 0.16 0.15 0.13 0.12 0.16 0.12 0.12 0.12 0.12 2 0.1407

var（cpi）-NS 0.22 0.18 0.17 0.13 0.15 0.15 0.13 0.12 0.12 0.14 4 0.1513

隨機游走 0.21 0.15 0.11 0.11 0.12 0.12 0.13 0.13 0.13 0.12 6 0.1316

AR 0.19 0.14 0.11 0.10 0.12 0.12 0.12 0.13 0.13 0.13 5 0.1300

2015 VAR 0.19 0.13 0.10 0.10 0.10 0.10 0.11 0.12 0.12 0.12 2 0.1205

AR-NS 0.18 0.12 0.10 0.11 0.12 0.11 0.11 0.13 0.15 0.16 4 0.1290

VAR-NS 0.23 0.15 0.14 0.13 0.14 0.12 0.12 0.14 0.16 0.17 7 0.1488

AR（cpi）-NS 0.18 0.12 0.09 0.10 0.12 0.10 0.11 0.12 0.14 0.16 3 0.1239

var（cpi）-NS 0.17 0.12 0.09 0.10 0.11 0.10 0.11 0.12 0.13 0.14 1 0.1185

表4 外推12個月預測誤差

外推12月 模型 1y 2y 3y 4y 5y 6y 7y 8y 9y 10y 排名 平均誤差

隨機游走 0.77 0.92 0.78 0.73 0.64 0.72 0.61 0.59 0.55 0.49 7 0.6812

2014 AR 0.49 0.64 0.44 0.36 0.26 0.36 0.26 0.26 0.25 0.22 5 0.3540

VAR 0.94 0.83 0.50 0.29 0.22 0.23 0.15 0.17 0.16 0.16 6 0.3642

AR-NS 0.26 0.21 0.16 0.11 0.13 0.17 0.13 0.17 0.17 0.16 1 0.1679

VAR-NS 0.37 0.31 0.22 0.12 0.13 0.14 0.12 0.15 0.15 0.13 4 0.1843

AR（cpi）-NS 0.30 0.24 0.18 0.12 0.09 0.17 0.13 0.17 0.17 0.16 2 0.1737

var（cpi）-NS 0.32 0.30 0.24 0.14 0.15 0.15 0.11 0.15 0.15 0.14 3 0.1842

隨機游走 0.77 0.62 0.47 0.44 0.45 0.37 0.33 0.33 0.33 0.33 7 0.4430

AR 0.67 0.54 0.40 0.38 0.38 0.34 0.31 0.33 0.35 0.36 6 0.4046

2015 VAR 0.36 0.27 0.15 0.13 0.12 0.14 0.16 0.18 0.20 0.21 2 0.1930

AR-NS 0.45 0.34 0.29 0.31 0.32 0.28 0.27 0.30 0.33 0.35 5 0.3237

VAR-NS 0.48 0.32 0.25 0.26 0.27 0.22 0.22 0.25 0.27 0.29 4 0.2827

AR（cpi）-NS 0.34 0.24 0.19 0.22 0.25 0.22 0.22 0.26 0.29 0.31 3 0.2551

var（cpi）-NS 0.29 0.18 0.12 0.14 0.16 0.14 0.16 0.18 0.21 0.23 1 0.1812

其次，本文采用AR-NS模型外推1期預測收益率曲線的水平值、斜率和曲率。結果顯示模型預測值的走向趨勢與實際值大體一致（如圖5至7所示）。分項看，2014年、2015年曲線水平值的年平均預測誤差分別為12.67BP、16.27BP；斜率的年平均預測誤差分別為17.54BP、25.77BP；曲率的年平均預測誤差分別為9.61BP、14.89BP。

圖5 AR-NS模型外推1期的水平值預測值與真實值（單位：%）

圖6 AR-NS模型外推1期的斜率預測值與真實值

圖7 AR-NS外推1期的曲率預測值與真實值

最后，本文采用AR-NS模型和VAR（CPI）-NS模型，外推12期預測收益率曲線的水平值、斜率和曲率。結果顯示，模型預測值的走向趨勢與實際值大體一致（如圖8至圖10所示）。

分模型看，AR-NS模型在2014年、2015年曲線水平值的年平均預測誤差分別為15.82BP、34.70BP；斜率的年平均預測誤差分別為32.89BP、26.97BP；曲率的年平均預測誤差分別為11.35BP、12.56BP。VAR（CPI）-NS模型在2014年、2015年曲線水平值的年平均預測誤差分別為13.81BP、22.77BP；斜率的年平均預測誤差分別為34.17BP、35.37BP；曲率的年平均預測誤差分別為20.24BP、27.32BP。從測試結果來看，VAR（CPI）-NS在水平值預測中更優，而AR-NS在斜率和曲率預測中更優，故本文在外推12期預測中，依然同時綜合參考兩個模型的預測結果。

圖8 外推12期的水平預測值與真實值（單位：%）

圖9 外推12期的斜率預測值與真實值

圖10 外推12期的曲率預測值與真實值

（二）對2016年中債國債收益率曲線的預測

本文基于2006年3月至2016年5月各期限中債國債即期收益率數據，構建AR-NS模型和VAR（CPI）-NS模型，并用兩種模型分別預測2016年6月至12月的 、 、 參數值及各期限債券的收益率。其中，VAR（CPI）-NS模型中的CPI采用Wind資訊宏觀預測中機構調查的均值。2016年6至12月，CPI的預測均值分別為1.9%、1.8%、1.6%、1.8%、2.1%、2.0%、2.0%。

兩個模型的預測結果為：（1）在2016年6月至12月，兩模型預測趨勢基本相同： 呈上升趨勢，而 、 呈下降趨勢，即水平參數逐步上升，斜率和曲率參數逐步下降。說明2016年全年收益率曲線整體呈逐月上升趨勢，并且期限利差呈逐步擴大的態勢。（2）各關鍵期限國債收益率即期利率水平的月均值以及波動區間如表5所示。由于VAR（CPI）-NS引入了CPI的預測值，且目前市場機構對2016年CPI預測均值處于歷史較低水平，故VAR（CPI）-NS的整體預測結果低于AR-NS模型。

圖11 對2016年中債國債收益率曲線 的預測值（單位：%）

圖12 對2016年中債國債收益率曲線 的預測值

圖13 對2016年中債國債收益率曲線 的預測值

表5 主要期限國債2016年6月至12月收益率預測結果（單位：%）

AR-NS VAR（CPI）-NS

期限 預測均值 預測區間 預測均值 預測區間

1年 2.34 [2.31，2.37] 2.19 [2.13 2.29]

3年 2.66 [2.60，2.72] 2.48 [2.46 2.55]

5年 2.91 [2.83，3.00] 2.78 [2.76 2.80]

7年 3.06 [2.95，3.15] 2.95 [2.91 3.00]

10年 3.17 [3.05，3.27] 3.08 [3.03 3.16]

注：

1. Nelson， C.R.， Siegel， A.F. Parsimonious Modeling of Yield Curves [J]. Journal of Business， 1987， 60（4）：4733-489.

2. Diebold， F.X. ， Li， C. Forecasting the Term Structure of Government Bond Yields [J]. Journal of Econometrics， 2006， 13（2）：337-364.

3. 張旭、李懷定：《債券市場中的執行利差》，國信證券固定收益研究報告，2010年9月。

作者單位：中國銀河證券

責任編輯：牛玉銳 羅邦敏