一種快速尋找最短路徑的算法

朱世宇 張洪明

摘要：最短路徑算法是計算機科學與地理信息科學等領域的研究熱點。從工業機械運動到城市道路網絡，最短路徑算法是其中不可或缺的一部分。最短路徑問題是圖論研究中的一個經典算法問題，旨在尋找由結點和路徑組成的圖中兩結點之間的最短路徑。主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止。本文介紹了一種以最鄰算法為基礎進行改進的算法。

關鍵詞：最短路徑 算法 圖論

中圖分類號：TP301 文獻標識碼：A 文章編號：1007-9416（2016）07-0115-02

1 引言

最短路徑算法是計算機科學與地理信息科學等領域的研究熱點。從工業機械運動到城市道路網絡，最短路徑算法是其中不可或缺的一部分。本文以試驗坐標點為例子討論了采用最短路徑算法的優勢，并提出了一種快速尋找最短路徑的算法。在很多文獻中，研究人員已提出過多種關于路徑優化的問題的求解算法[1～4]。本文在綜合最優路徑的算法研究上主要提出了1種基于最鄰算法的改進算法。

2 區域最鄰算法

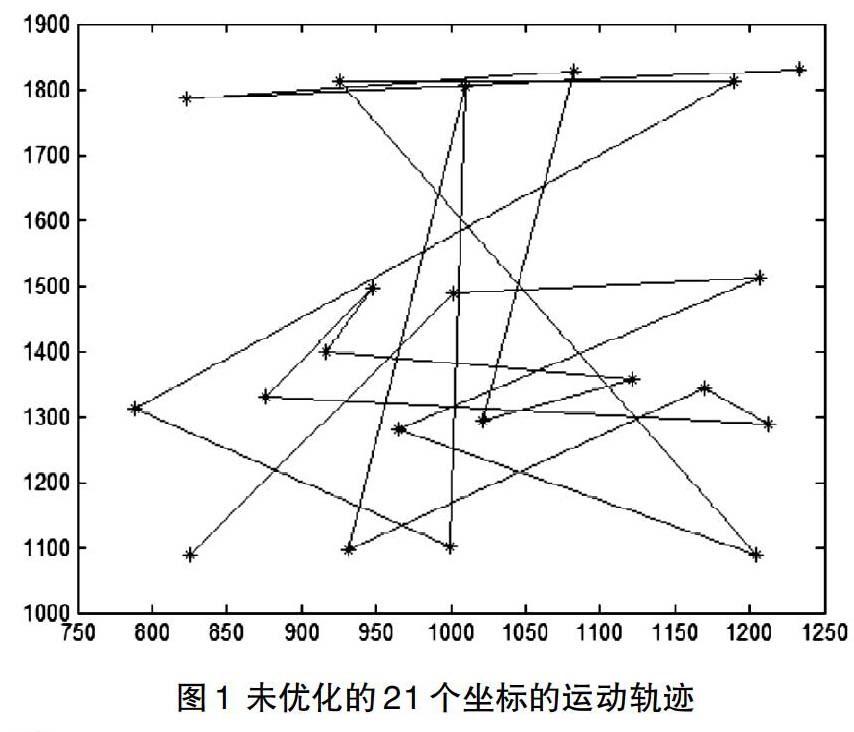
以表1所示的坐標進行試驗，在未進行優化的時候，按其原有的排列順序進行移動，其運動軌跡如圖1所示，以試驗坐標點為單位，從第一個點到最后一個點運動路程共7252.39。

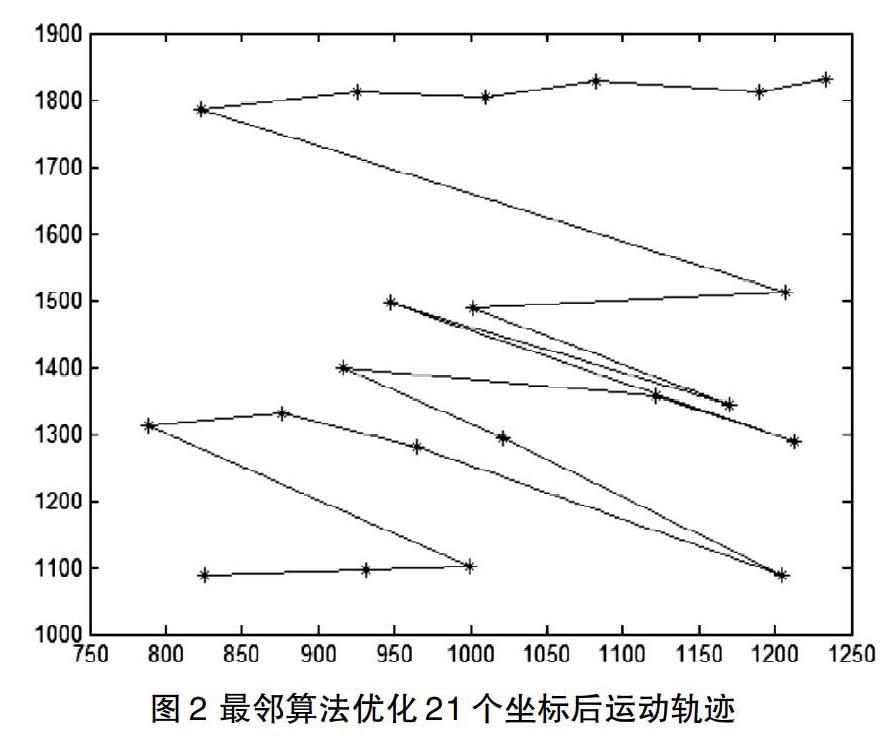
從圖1可以看出，未對坐標進行優化之前，運動軌跡非常的混亂。使用最鄰算法對表1坐標進行排序后，得到表2，按其排列順序進行移動，其運動軌跡如圖2所示，以坐標為單位，從第一個點到最后一個點運動路程共3642.559。

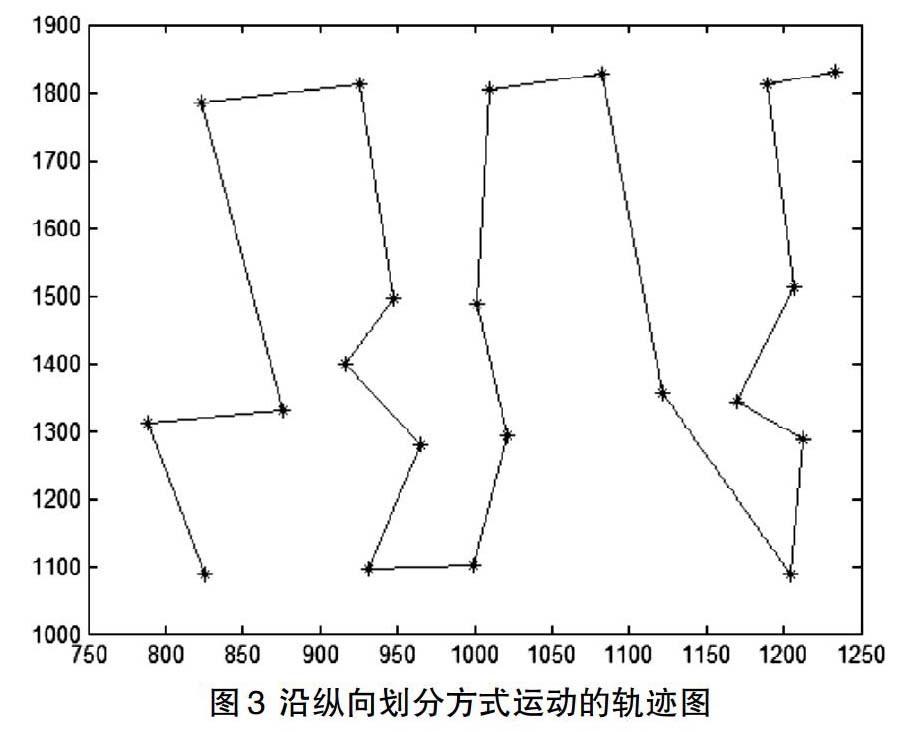
圖2的移動的路徑較之前的運行軌跡更加合理[5]，但是經過研究其實還有提升的空間。本文在最近鄰方法上，進行了改進，使用了一種區域劃分的方式將整個打坐標分布的區域劃分別劃分為橫縱的5行。如果是以縱向的寬度劃分區域的話，那么從第一行起，坐標的排列順序為橫向從小到大排列，而第二行則是從大到小，第三行再從小到大，以此類推。而如果是以橫向劃分區域，則是以縱向進行大小排列。以縱向劃分方式對表1中的坐標排序后，得到表3，按其排列順序進行移動，其運動軌跡如圖3所示，以坐標為單位，從第一個點到最后一個點運動路程共4004.745。

3 結語

以試驗坐標為例，優化后的機械手移動路徑比未經優化的路徑節約路程7252.39-2324.798=4927.59，節省了約原來一半多的的路程。

參考文獻

[1]Wu C G， Liang Y C ， Lee H P ， et al. Generalized chromosome genetic algorithm for generalized traveling salesman problems and its applications for machining[J]. Physical Review E ， 2004 ， 70（1）：1～13.

[2]Dimitrijevic V ， Saric Z. Efficient transformation of the generalized traveling salesman problem into the traveling salesman.problem on digraphs[J].Information Sciences，1997，102（1～4）：105～110.

[3]Lien Y N ， Ma E ， Wah Benjamin W S. Transformation of the generalized trav-eling-salesman an problem into the standard trav2eling2salesman problem[J].Information Sciences，1993，74（1～2）：177～189.

[4]Tsai I C F ， Tsai C W， Tseng C C. A new hybrid heuristic approach for solving large traveling salesman problem[J].Infor2 mation Sciences，2004，166（1～4）：67～81.

[5]趙赫，杜端甫.TSP的鄰域搜索算法的分析和改進[J].中國管理科，1997，5（1）：35～39.