機載線性調頻脈沖壓縮雷達雜波模型的研究
唐 斌, 莫 磊, 蔡昌勇, 李 莉
( 1. 電子科技大學 電子工程學院, 四川 成都 611731; 2. 成都航空職業技術學院 航空電子工程系, 四川 成都 610100; 3. 四川省高校校企聯合“航空電子技術”應用技術創新基地, 四川 成都 610100)
機載線性調頻脈沖壓縮雷達雜波模型的研究
唐 斌1,2,3, 莫 磊2,3, 蔡昌勇2,3, 李 莉2,3
( 1. 電子科技大學 電子工程學院, 四川 成都 611731; 2. 成都航空職業技術學院 航空電子工程系, 四川 成都 610100; 3. 四川省高校校企聯合“航空電子技術”應用技術創新基地, 四川 成都 610100)
與常規脈沖雷達相比,由于疊加效應,線性調頻(LFM)脈沖壓縮雷達的雜波信號模型有其特殊性.機載雷達與地面雷達相比,由于載機的運動會引起各個雜波單元回波多普勒頻率的不同,其雜波模型更為復雜.針對LFM脈沖壓縮信號及機載雷達各自的特性,提出了應用在機載雷達上的LFM脈沖壓縮信號雜波模型,并對脈壓前后雜波的統計特性進行仿真和分析,仿真結果表明新模型的有效性.
線性調頻脈沖壓縮雷達; 機載雷達; 雜波; 脈沖壓縮; 統計特性
大時帶積LFM信號作用距離遠、距離分辨率高,與常規雷達相比,大時帶積信號的雜波模型有其特殊性.文獻[1-2]研究了發射信號為偽碼調相連續波情況下回波信號的特點,指出各個碼元回波之間會產生重疊,并對其統計性質做了分析.文獻[3]論述了在低俯仰角情況下,LFM脈壓回波信號展寬問題,并通過蒙特卡羅仿真給出了LFM信號下雜波模型的統計特性,但沒有進行脈壓后雜波模型的統計性能分析.機載雷達與一般常規地面雷達相比,雜波模型更為復雜.由于雷達載機的運動,地面雜波回波多普勒譜被大大展寬[4-5],影響了接收機的檢測性能[6-8].LFM脈壓信號與機載雷達各有其特點,要將二者更好的結合在一起進行取長補短,就必須結合這二者各自的特點,綜合進行環境和目標特性的研究.
本文在前人研究的基礎上,結合機載雷達及LFM脈壓信號各自的特殊情況,提出了適用于機載雷達LFM脈壓信號的雜波模型,并以蒙特卡羅方法,仿真并分析了模型的統計特性,得到了一些新的結論.
1 常規體制脈沖雷達及LFM脈壓雷達的雜波模型
根據相干視頻模擬原理[9-10],常規脈沖體制下,第n個隨機散射體的第m個脈沖回波視頻信號模型為
(1)

多個隨機散射體的第m個脈沖視頻回波為各個散射體回波的復數和
(2)
可以看出,假設復調制函數u(t)的脈沖寬度為T,散射體彼此之間的徑向距離等于或超過cT/2時(c為光速),各個隨機散射體的回波彼此不會重疊,這是常規脈沖體制下的雜波模型.
根據雷達分辨理論[11-12],雷達距離分辨率主要取決于雷達信號帶寬B,距離分辨率為c/2B.常規脈沖雷達距離分辨率為cT/2,這是由于常規脈沖信號時寬和帶寬有T≈1/B的關系.而LFM脈壓信號的距離分辨率為cτ/2或c/2B,其中,τ=T/D,D為壓縮比,T為時寬,τ為脈壓后的時寬.
如圖1所示,低仰角情況下,常規脈沖雷達的徑向距離分辨單元長度為cT/2,即波束涵蓋的徑向長度.由于壓縮比D往往很大,在常規脈沖雷達距離分辨單元內,就有Nc=TB個LFM脈壓雷達的距離分辨單元.
和常規雷達的概念相對應,在整個主波束里,分成Nc個子波束,每一個子波束對應地面徑向長度為c/2B的距離分辨單元.將這樣的距離分辨單元映射到雷達坐標中,得到其距離門的寬度為τ=1/B.
圖2表明了徑向距離分辨率為c/2B的地面雜波單元回波信號與距離門之間的關系.由于每一個雜波單元的回波信號持續脈沖寬度為T,而距離門寬度為τ=1/B,在這種情況下,各個雜波單元回波信號彼此會有重疊,各個距離門回波可以看成是多個雜波單元回波的疊加,這就是LFM脈壓信號體制下的雜波模型.


為了分析的方便,將整個寬度為T的LFM信號按(3)式劃分為Nc個寬度為τ=1/B的子脈沖序列.
0≤t≤T.
(3)

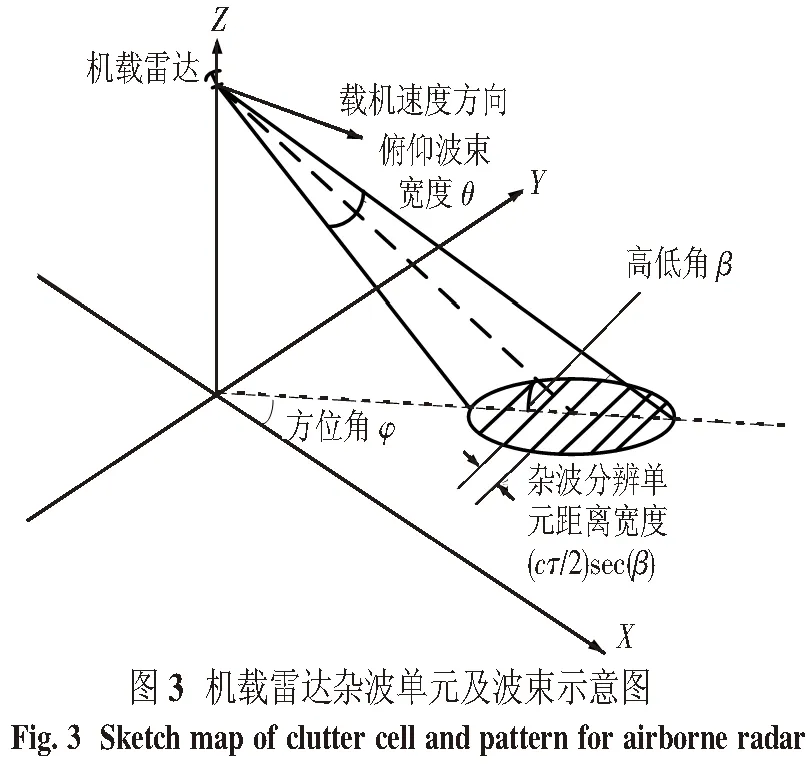
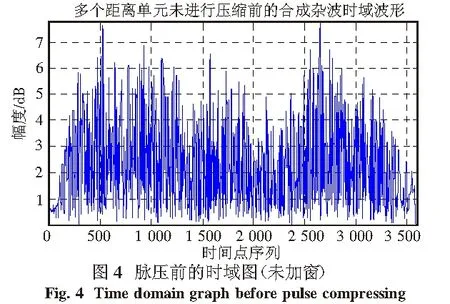
0 (4) 第k個距離門的合成回波為 (5) 將(4)式帶入(5)式有 (6) 設雷達位置在載機正側面,如圖3所示,載機速度方向為X軸,大小為v,高度為H,主波束中心方位角為φ,高低角為β,主波束俯仰寬度θ,雷達波長為λ. 設初始時刻,主波束中心雜波單元的坐標為(X0,Y0,0),其與載機雷達的間距為 (7) t時刻的間距為 R2(t)=(R0cosφcosβ-vt)2+ (8) 載機與雜波單元的相對運動造成的雷達信號相位變化φ(t)可以近似地考慮為 φ(t)=2π(fdt+fdst2/2), (9) 式中 fd=2v(cosφcosβ)/λ, (10) (11) fds這個LFM項可以用已知的技術進行補償,所以本文中將其略去.主波束中心雜波單元的多普勒頻移為 fd=2v(cosφcosβ)/λ. (12) 當機載雷達為LFM雷達時,對主波束探測到的區域,按高低角的不同,雜波分辨單元按前述子波束的定義劃分為條狀區域,其中雜波分辨單元的長度為(cτ/2)secβ,τ為時寬(LFM信號的子脈沖寬度).由于載機的運動,不同高低角的雜波單元的多普勒頻率fd不同,方位角為φ,高低角為β-θ/2+nθ/Nc的第n個雜波單元的多普勒頻率為[13-14] fnd=2vcosφcos(β-θ/2+nθ/Nc)/λ. (13) 實際仿真中,都是將這些條狀區域作為隨機點散射體處理,將各個隨機點散射體的回波信號進行合成處理.考慮到機載預警雷達的視野開闊,波束較寬、波長較短的特點,可以認為各個雜波單元的回波為獨立分布的復隨機信號. 根據以上的分析,第n個雜波單元回波為 (14) Kn和φn分別是雜波單元回波的隨機幅度及隨機相位,被認為是互相獨立的隨機量. 中國電波研究所對平原、丘陵和山區等典型地形進行了雷達雜波特性測試,發現韋布爾分布對實測數據的擬合較好,所以本文認為Kn是服從韋布爾分布的隨機量,φn是服從(0,2π)均勻分布的隨機量.根據文獻[11,13-14],Kn和φn皆為慢時間變化量,在一個脈沖寬度T內Kn和φn近似保持不變.韋布爾的概率密度函數 f(x/a,b)=abxb-1e-axb,x>0. (15) 韋布爾分布所用的尺度參數a和形狀參數b,由文獻[15]中X波段實測數據確定為a=5,b=1. 結合(4)~(14)式,可以推出機載LFM雷達第k個距離門的合成回波為 ej4πvcos φcos(β-θ/2+nθ/Nc)t/λejφn. (16) 根據某型機載雷達的參數,假定:一個波束范圍內雜波單元數目Nc=800,定義800個距離門,B=10 MHz,T=80 μs,脈沖重復頻率fr=1 000 Hz,波長為0.1 m,方位角45°,高低角45°,載機速度為700 km/h,主波束俯仰寬度2°.考慮到一個子脈沖內統計性能相同,為簡化起見,采樣率設為10 MHz.根據(16)式,對機載LFM雷達各個距離門的合成回波做5 000次蒙特卡羅仿真試驗,確定其幅度及相位分布的統計特性. 3.1 雜波幅度分布特性 對第15、60、300個距離門的合成回波幅度概率密度分布與標準韋布爾分布進行比較仿真分析,如表1所示.對合成回波仿真數據進行參數估計而得到對應的韋布爾分布的參數a、b,這里a表示尺度參數,b表示形狀參數.當距離門個數變大,即疊加的雜波回波信號個數增加時,尺度參數a減小,合成雜波平均功率增大;形狀參數b趨向于2,距離門的合成回波幅度趨向于瑞利分布,體現了疊加效應.值得注意的是,再將帶寬降為1.25 MHz,采樣率為1.25 MHz,做同樣的仿真,仿真結果表明,上述規律不變,這表明對于合成回波幅度分布的“瑞利化”,帶寬B起的作用很小,起主要作用的還是回波的疊加次數. 表 1 參數比較 3.2 雜波相位分布特征 根據上述理論,把(0,2π)內均勻分布的雜波相位分布與第15、60、300個距離門內相位的分布進行仿真比較.結果表明,各個距離門內的相位分布是在(0,2π)的均勻分布. 由上述合成回波幅度及相位分布可知,當多個獨立雜波單元回波按(16)式進行線性疊加時,其合成雜波幅度趨向瑞利分布,相位趨向(0,2π)的均勻分布.這表明合成后雜波復信號的實部及虛部分布皆趨向于相互獨立的高斯分布,同時也說明各個雜波單元回波信號對于合成雜波起的作用基本相同,并沒有一個回波信號起主導作用.仿真結果還表明,隨著疊加次數的增加,這樣的趨勢越來越明顯. 3.3 脈壓后的幅度分布 對于LFM脈壓信號來說,了解脈壓后峰值點幅度的分布更具有實際意義.對此,假定:一個波束范圍內雜波單元數目Nc=800,800個距離門,B=1.25 MHz,T=80 μs,采樣率5 MHz,脈沖重復頻率fr=1 000 Hz,波長為0.1 m,方位角45°,高低角45°,載機速度為700 km/h,主波束俯仰寬度2°.按(16)式合成回波,再對合成回波作脈壓處理,同樣做5 000次蒙特卡羅仿真試驗,確定其幅度、相位分布的統計特性.考慮到LFM信號對多普勒效應不敏感,所以以發射信號的共軛移位作為匹配濾波器的沖擊響應. 脈壓使用頻域快速卷積法,即 y(n)=s(n)*h(n)= IFFT(FFT(s(n))×FFT(h(n))), (17) h(n)為發射信號的共軛移位. 圖4表示脈壓前的時域合成雜波幅度波形,圖5表示脈壓后的時域幅度波形.為了全面了解脈壓對幅度的影響,主波束內第一個雜波單元回波到達接收機匹配濾波器時間設為時間軸原點,同時,為了避免和前面距離門定義相混淆,對脈壓后時間位置,用時間軸數值點來表示.因此,第1個雜波單元回波信號脈壓后的峰值所在坐標應為400,第800個雜波單元的回波信號的脈壓峰值所在坐標應為3 600. 圖6和圖9分別表示脈壓后時間軸上300點及3 900點上的幅度概率分布,可見,在被充分脈壓前(第400個點以前及3 600點以后),前述疊加效應仍起主要作用,各個峰值點幅度分布趨向于瑞利分布.從400點開始到3 600點,由圖7和圖8可見,脈壓效應開始起作用,脈壓后峰值幅度分布與300點有顯著的變化,有很明顯的拖尾現象,可以用韋布爾分布近似進行定性分析.由圖看出,與脈壓前單個雜波單元的回波幅度分布參數(a=5,b=1)相比,脈壓后尺度參數a顯著減小,表明雜波平均功率大幅增加,形狀參數b增加,表明幅度分布趨向于均勻,分布的方差變小.對于這個結果,我們是這樣分析的:對于脈壓處理前的合成回波,疊加效應起主導作用,盡管各個雜波單元的回波幅度為韋布爾分布,但其單個回波對合成回波起的作用基本相同,所以合成回波的幅度分布趨向于瑞利分布,相位趨向于(0,2π)的均勻分布.進行脈壓處理后,雜波單元的回波長脈沖(T)的能量被壓縮在一個短脈沖(τ)內,其峰值點是由這個雜波單元回波脈壓后主瓣與相鄰雜波單元回波脈壓后旁瓣進行復數疊加而成,即峰值點的數值要受與其相鄰雜波單元回波脈壓的旁瓣影響,但相對于這個主瓣來說,旁瓣的數值相對較小,對統計性能起主要作用的還是這個雜波單元的回波信號本身的統計特性及脈壓效果,所以脈壓后其峰值幅度仍近似韋布爾分布,但尺度參數a減小,體現了主瓣的影響;形狀參數b變大,體現了旁瓣的影響.為了與上述的疊加效應相對應,本文將這樣結果稱之為脈壓效應. 仿真發現,加窗后的脈壓幅度概率分布同樣在400點與3 600點之間近似表現為韋布爾分布,其它點幅度趨向于瑞利分布.同時,尺度參數a降低得更小,形狀參數b增加得更大.按照上面的分析,這是由于加窗后的主旁瓣都降低,但與主瓣相比,旁瓣降低得更多,旁瓣的影響隨之減小,所以參數上表現為尺度參數a更小,表明雜波平均功率增大;主瓣變寬,使得形狀參數b增大,表明幅度分布更趨向于均勻,體現了脈壓效應. 仿真數據同時表明,脈壓后的相位分布是在(0,2π)的均勻分布,在此由于篇幅所限,不再將圖列出. 本文在前人研究的基礎上,提出了機載LFM脈壓雷達的雜波模型,并通過蒙特卡羅仿真試驗方法,對其脈壓前后不同距離門內雜波幅度及相位的統計特性進行了分析,得出了以下結論:在脈壓前,距離門回波是由多個雜波單元回波線性疊加而成,隨疊加次數的增加,其幅度趨向于瑞利分布,其相位趨向(0,2π)均勻分布,體現了疊加效應.在脈壓后,由于脈壓的作用,其幅度近似趨向于韋布爾分布,與單個雜波單元回波幅度分布(韋布爾分布,a=5,b=1)相比,脈壓后峰值點幅度的參數a和b表明,平均功率增大,方差減小,大小分布更加均勻.在加窗脈壓后,其幅度的分布統計性能與未加窗脈壓信號稍有不同,這是脈壓本身的性質形成的,體現出脈壓效應.這些結論為設計機載LFM脈壓雷達背景下信號檢測及恒虛警處理算法提供了理論基礎,具有一定的參考價值. [1] 王志華,趙兆,蔡征宇. 基于S-method的偽碼調相連續波雷達調頻干擾抑制[J]. 南京理工大學學報(自然科學版),2011,35(6):858-862. [2] 曹軍亮,牟連云,楊網成,等. 偽碼調相連續波雷達模糊函數推導及仿真分析[J]. 艦船電子對抗,2011,34(1):64-68. [3] 張長隆. 線性調頻脈沖壓縮雷達雜波統計模型分析[J]. 電波科學學報,2004,19(2):240-244. [4] 唐斌,曾偉一,曾友州,等. 機載相控陣雷達陣元幅相誤差下的空時雜波譜[J]. 四川師范大學學報(自然科學版),2010, 33(S):476-479. [5] FERTIG L B. Analytical expressions for space-time adaptive processing (STAP) performance[J]. IEEE Transactions on Aerospace and Electronic Systems,2015, 51(1):442-453. [6] 曾偉一,唐斌,曾友州,等. 提高空時自適應處理穩健性的一種新方法[J]. 四川師范大學學報(自然科學版),2010,33(5):711-714. [7] BANG J H, MELVIN W L, LANTERMAN A D. Model-based clutter cancellation based on enhanced knowledge-aided parametric covariance estimation[J]. IEEE Transactions on Aerospace and Electronic Systems,2015,51(1):154-166. [8] EL KHATIB A, ASSALEH K, MIR H. Space-time adaptive processing using pattern classification[J]. IEEE Transactions on Signal Processing,2015,63(3):766-779. [9] MITCHELL R L. 雷達系統模擬[M]. 陳訓達,譯. 北京:科學出版社,1982. [10] 花漢兵. 雷達雜波模型的建立與仿真[J]. 計算機仿真,2007,24(10):92-94. [11] SKOLNI K, MERRILL I. Radar Handbook[M]. 3rd ed. New York:McGraw Hill,2008. [12] 向敬成,張明友. 雷達系統[M]. 北京:電子工業出版社,2001. [13] MAHAFZA B R. Radar Signal Analysis and Processing Using Matlab[M]. New York:Taylor & Francis Group,2009. [14] HERBERT G M. Clutter modeling for space-time adaptive processing in airborne radar[J]. IET Radar, Sonar, Navigation,2010,4(2):178-186. [15] 羅賢云,張忠治. 地物雷達雜波空間相關特性的測量與分析[J]. 電波科學學報,1995,10(3):50-56. (編輯 李德華) Research on Clutter Model for Airborne Linear Frequency Modulated Pulse Compression Radar TANG Bin1,2,3, MO Lei2,3, CAI Changyong2,3, LI Li2,3 ( 1. School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, Sichuan; 2. Department of Electronic Engineering, Chengdu Aeronautic Polytechnic, Chengdu 610100, Sichuan; 3. The Innovation Base of School-Enterprise Cooperation Aviation Electronic Technology in Sichuan, Chengdu 610100, Sichuan Compared to the traditional pulse radar, the clutter statistical model for linear frequency modulated (LFM) pulse compression radar has intrinsic special properties because of the superimposed effect. For the airborne radar, the Doppler frequency of echo signal of each clutter cell is different due to the motion of the platform. Relative to the land-based radar, the statistical clutter model of airborne radar is more complicated. In this paper, towards the characteristics of LFM signal and airborne radar, a statistical clutter model suitable for airborne radar that employs LFM waveforms is presented. The new statistical clutter model is analyzed and simulated before and after pulse compressing. The results prove the effectiveness of the proposed model. linear frequency modulated pulse compression radar; airborne radar; clutter; pulse compression; statistical characteristics 2015-04-20 國家自然科學基金(U1433129)、中國博士后科學基金(2012M511919)和四川省教育廳重點科研項目(14ZA0307) 唐 斌(1974—),男,副教授,主要從事陣列自適應信號處理、測控技術、衛星信號等技術的研究,E-mail:tbuestc@163.com TN957 A 1001-8395(2016)06-0929-06 10.3969/j.issn.1001-8395.2016.06.0282 機載雷達雜波模型

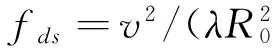
3 統計特性分析






4 結論

