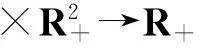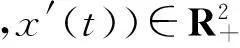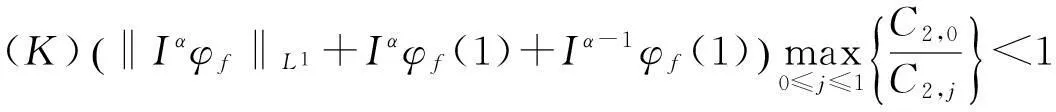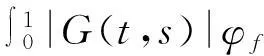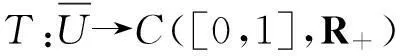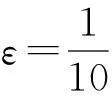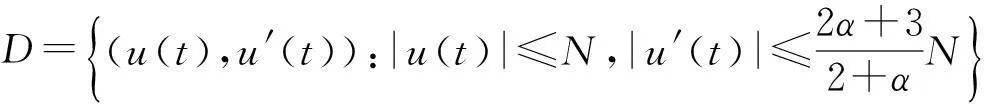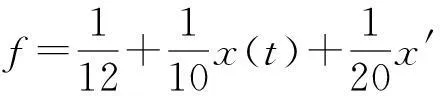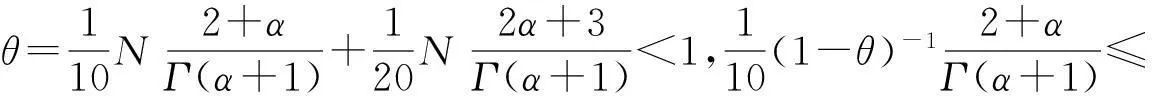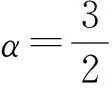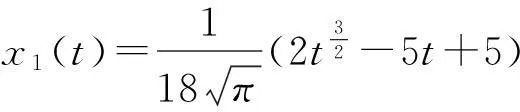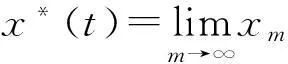分?jǐn)?shù)階微分方程邊值問(wèn)題的Picard’s迭代方法

孫宇鋒，曾廣釗

(韶關(guān)學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 中國(guó) 韶關(guān)　512005)

?

分?jǐn)?shù)階微分方程邊值問(wèn)題的Picard’s迭代方法

孫宇鋒*，曾廣釗

(韶關(guān)學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 中國(guó) 韶關(guān)512005)

摘要從分?jǐn)?shù)階微分方程邊值問(wèn)題的近似解出發(fā)，應(yīng)用Picard’s迭代方法證明了其存在唯一解；研究了非線性函數(shù)f(t;x(t),x′(t))由一個(gè)函數(shù)序列{fm(t;x(t),x′(t))}近似代替時(shí)，邊值問(wèn)題解的Picard’s迭代序列滿足的形式及其存在唯一解的充要條件；討論了這類邊值問(wèn)題不考慮近似解以及非線性函數(shù)Lipschitz類的因素時(shí)，其解的一般性存在條件；最后通過(guò)兩個(gè)數(shù)值算例驗(yàn)證了這類邊值問(wèn)題解的存在性以及解與其迭代序列的誤差估計(jì).

關(guān)鍵詞分?jǐn)?shù)階微分方程；迭代方法；近似解；誤差估計(jì)

本文在文獻(xiàn)[1～7]的基礎(chǔ)上，討論基于Caputo’s分?jǐn)?shù)導(dǎo)數(shù)的一類分?jǐn)?shù)階微分方程的邊值問(wèn)題, 并通過(guò)其近似解的Picard’s迭代序列，得到相應(yīng)的解的存在性和唯一性定理.

考慮如下分?jǐn)?shù)階微分方程的邊值問(wèn)題

(1)

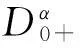
1預(yù)備知識(shí)

這一節(jié)給出Caputo’s分?jǐn)?shù)導(dǎo)數(shù)和Riemann-Liouville分?jǐn)?shù)積分的定義(見文獻(xiàn)[8])以及幾個(gè)概念和引理.

定義1設(shè) h(t)∈C1([0,1],R+)，則下面積分

稱為h(t)的Riemann-Liouville分?jǐn)?shù)積分, 這里Γ(α)是Γ-函數(shù)，α∈R+.

定義2設(shè)h(t)∈C1([0,1],R+)，則h(t)的α階Caputo’s分?jǐn)?shù)導(dǎo)數(shù)由下式定義：

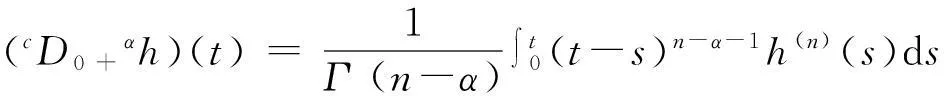
這里n=[α]+1，α∈R+.

定義3一個(gè)函數(shù)x(t)稱為(1)的解. 如果 ①x(t)∈C1([0,1],R+)， ②x(t)滿足(1)的條件，③ 方程 (1) 對(duì)于t∈[0,1] 成立.

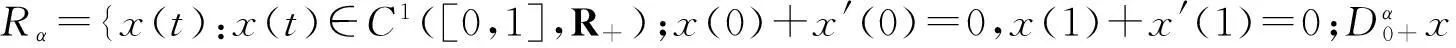
引理1[4]若x(t)∈Rα，則x(t) 是(1)的解的充要條件是

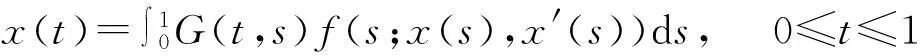
引理2[4]對(duì)于格林(Green’s)函數(shù)G(t,s)，下列不等式成立

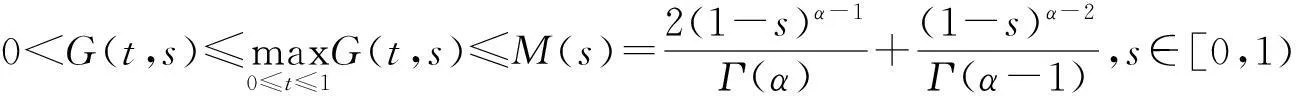
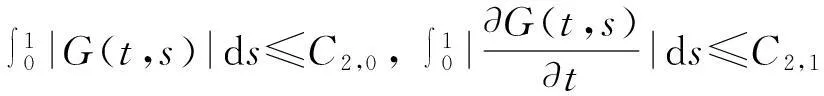
定義4一個(gè)函數(shù)z(t) 稱為邊值問(wèn)題(1)的近似解, 如果存在ε>0使得

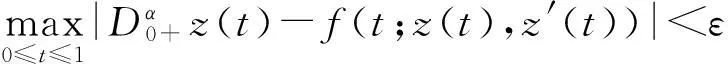
并且，下面條件成立z(0)+z′(0)=0,z(1)+z′(1)=0.

由引理1可知, 近似解z(t)可以被表示成

(2)

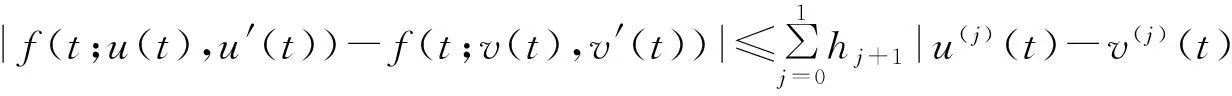
容易驗(yàn)證，對(duì)于x(t)∈Rα, 如下定義范數(shù)‖x‖，則Rα是 Banach空間.

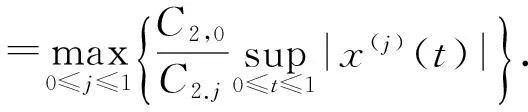
引理3[9]令B是一個(gè)Banach空間，S(x0,r)={x∈B:‖x-x0‖0. 令T將S(x0,r) 映射到B, 并且

① 對(duì)于所有的x,y∈S(x0,r),‖Tx-Ty‖≤ρ‖x-y‖，這里 0<ρ<1，

②r0=(1-ρ)-1‖Tx0-x0‖≤r.則有：

(1)T在S(x0,r)里有唯一不動(dòng)點(diǎn)x*.

(2) 序列{xm}：其中xm+1=Txm,m=0,1,2,… 收斂到x*，而‖x*-xm‖≤ρmr0.

2主要結(jié)果

定理1假設(shè)邊值問(wèn)題(1)存在一個(gè)近似解z(t)，并且

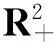
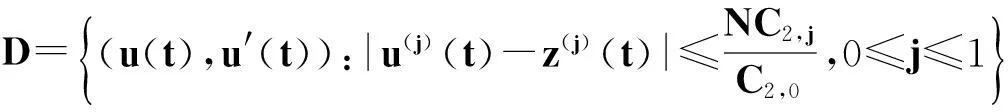
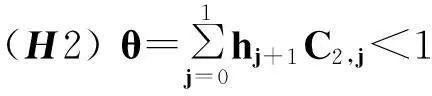
(H3) ε(1-θ)-1C2,0≤N.

則有結(jié)論：

① 在S(z,N)={x(t)∈Rα:‖x-z‖0}中存在邊值問(wèn)題(1)的唯一解x*(t).

② 序列{xm(t)}收斂到x*(t).這里{xm(t)}稱為近似解z(t)的Picard’s迭代序列，滿足

(3)

x0(t)=z(t)，且有如下誤差估計(jì)：‖x*-xm‖≤θmN0,N0=(1-θ)-1‖x1-x0‖.

(4)

G(t,s)是邊值問(wèn)題(1)的格林(Green’s)函數(shù)，有xm+1(t)=Txm(t),m=0,1,2,….則 T:Rα→Rα是全連續(xù)映射(見文獻(xiàn)[4]).

z(t)∈S(z,N)，由Rα上的范數(shù)定義, 知(z(t),z′(t))∈D.

如果 x(t),y(t)∈S(z,N) 應(yīng)用引理1和引理2, 有：

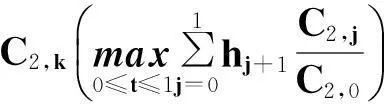
更進(jìn)一步, 有:

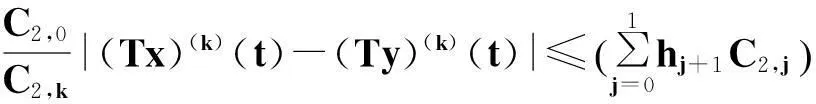
即‖Tx-Ty‖≤θ‖x-y‖.

在勞拉看來(lái)，相比于保時(shí)捷911 GT2 RS偏軟的底盤，她更喜歡邁凱倫的硬朗，雖然這并不會(huì)影響圈速的排名。對(duì)于經(jīng)驗(yàn)尚淺的駕駛者來(lái)說(shuō)，駕駛邁凱倫跑出的圈速通常優(yōu)于保時(shí)捷，但對(duì)于職業(yè)車手來(lái)說(shuō)則恰恰相反。換言之，保時(shí)捷911 GT2 RS擁有更高的極限，但前提是駕駛者對(duì)其特性的了然于心。

再次應(yīng)用引理1 和引理2,得到|(Tz)(k)(t)-z(k)(t)|≤εC2,k,0≤k≤1，

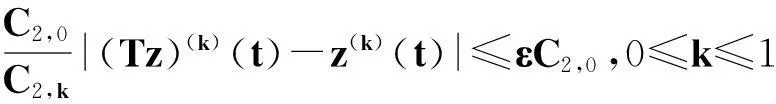
即 ‖Tz-z‖≤εC2,0，由條件(H3), 有 (1-θ)-1‖Tz-z‖≤N.

這樣，滿足引理3 的條件.因此，定理1 中的結(jié)論①～② 成立.

定理1通過(guò)求解近似解的Picard’s迭代序列(3)得到了邊值問(wèn)題(1)的唯一解.然而，在實(shí)際應(yīng)用中，函數(shù)f(t;x(t),x′(t))可以由一個(gè)函數(shù)序列{fm(t;x(t),x′(t))}近似得到.此時(shí)的Picard’s迭代序列{ym(t)}滿足如下形式：

(5)

y0(t)=z(t).

(H4) 對(duì)于fm(t;x(t),x′(t))，如果 ?y(t)∈S(z,N)，存在Δ≥0，使得下面不等式成立：

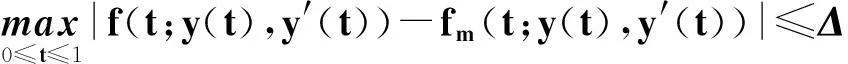
則稱函數(shù)序列{fm(t;x(t),x′(t))}絕對(duì)近似到f(t;x(t),x′(t)).因此，有如下結(jié)論.

定理2假設(shè)邊值問(wèn)題(1)存在一個(gè)近似解z(t)，并且

(H5) 滿足定理1 中的條件(H1)～(H2)，以及(H4)，

(H6) N1=(ε+Δ)(1-θ)-1C2,0≤N.

則有結(jié)論：

Ⅰ. 定理1中的結(jié)論①～② 成立.

Ⅱ. 由(5)得到的Picard’s序列{ym(t)}?S(z,N1)={y(t)∈Rα:‖y-z‖0}.

Ⅲ. 序列{ym(t)}收斂到邊值問(wèn)題(1)的唯一解x*(t)，當(dāng)且僅當(dāng)

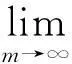
此外

‖x*-ym+1‖≤(1-θ)-1(θ‖ym+1-ym‖+ΔC2,0).

(6)

證Δ≥0，則ε(1-θ)-1C2,0≤N1≤N，所以，結(jié)論Ⅰ成立.

為了證明結(jié)論Ⅱ，注意到，z(t)∈S(z,N1)，如果y(t)∈S(z,N1)，只須證明Ty(t)∈S(z,N1)即可.此處算子T如下定義：

(7)

為此，從(2)和(7)式，有：

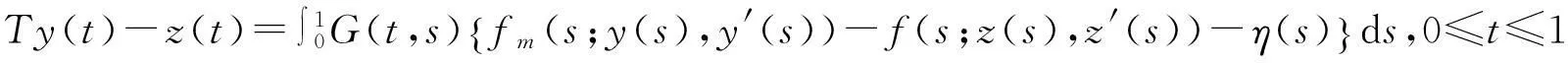
即

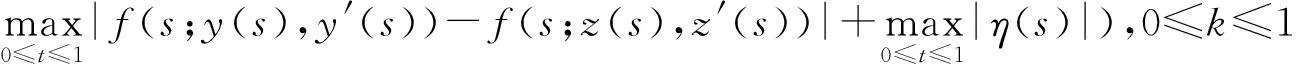
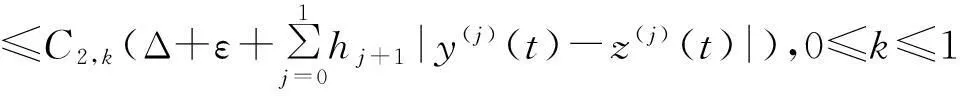
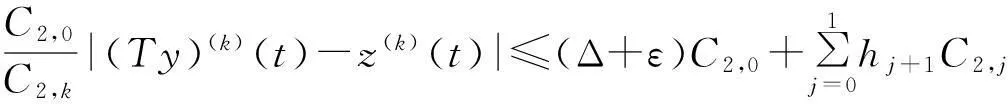
即， ‖Ty-z‖≤(1-θ)N1+θ‖y-z‖≤(1-θ)N1+θN1=N1，所以，Ty(t)∈S(z,N1).

由式(5)和(7)知，結(jié)論Ⅱ成立.

下面證明結(jié)論Ⅲ.由xm+1(t)和ym+1(t)的定義知：

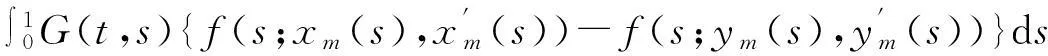
類似于定理1的證明，有：

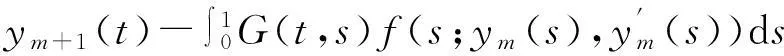
(8)

現(xiàn)在對(duì)xm(t)-ym(t)進(jìn)行相似的討論，反復(fù)應(yīng)用式(8)，并且注意x0(t)=y0(t)=z(t)得

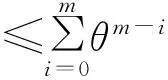
(9)

對(duì)式(9)應(yīng)用三角不等式，得到：

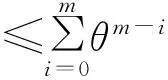
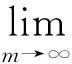
最后，證明式(6).為此，注意到：

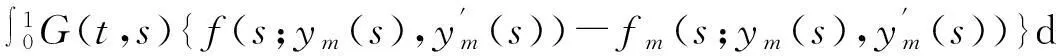
與以前的證明類似，有：

‖x*-ym+1‖≤θ‖x*-ym‖+ΔC2.0≤θ‖x*-ym+1‖+θ‖ym+1-ym‖+ΔC2.0.

因此， ‖x*-ym+1‖≤(1-θ)-1{θ‖ym+1-ym‖+ΔC2.0}.

(H7) 對(duì)于fm(t;x(t),x′(t))，如果 ?y(t)∈S(z,N)，存在 0≤ω≤1，使得下面不等式成立：

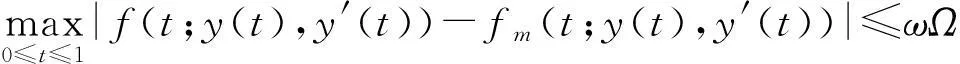
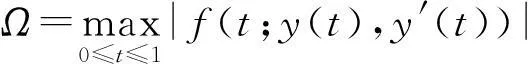
定理3假設(shè)邊值問(wèn)題(1)存在一個(gè)近似解z(t)，并且

(H8) 滿足定理1 中的條件(H1)，以及(H7)，

(H9) ?=(1+ω)θ<1，

(H10)N2={ε+ω(1-ω)-1Ω}(1-?)-1C2,0≤N.

則有結(jié)論：

(Ⅰ) 定理1中的結(jié)論①～② 成立.

(Ⅱ) 由式(5)得到的Picard’s序列{ym(t)}?S(z,N2)={y(t)∈Rα:‖y-z‖0}.

(Ⅲ) 序列{ym(t)}收斂到邊值問(wèn)題(1)的唯一解x*(t)，當(dāng)且僅當(dāng)

此外

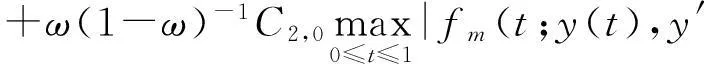
(10)

證類似于定理2的證明，此處省略.

注記如果{fm(t;x(t),x′(t))}是Lipschitz類序列且一致收斂于{f(t;x(t),x′(t))}，則定理2，定理3中的結(jié)論顯然成立.并且式(6)由下式替代：

‖x*-ym+1‖≤(1-θ)-1(θm‖y1-y0‖+ΔC2,0),

式(10)由下式替代：

‖x*-ym+1‖≤(1-θ)-1{θm‖y1-y0‖+ω(1-ω)-1C2,0Ω}.

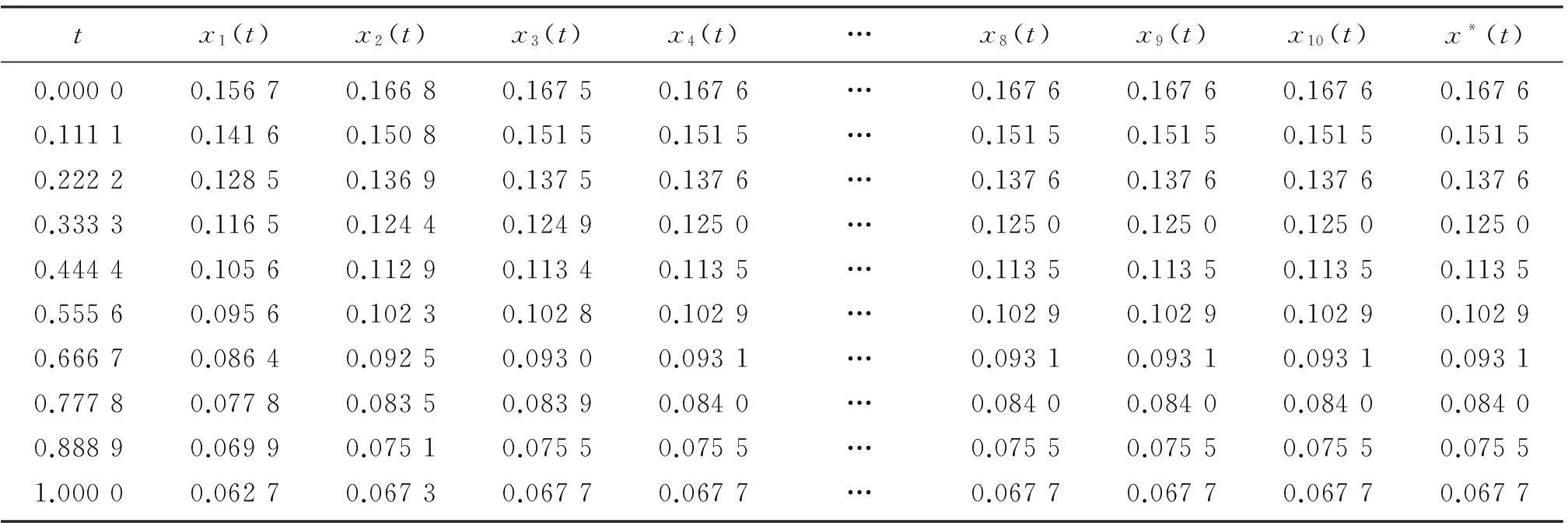
如果不考慮近似解以及Lipschitz類的因素，可以得到邊值問(wèn)題(1)解的一般存在性結(jié)果.

(H11)f(t;x(t),x′(t))是[0,1]上的連續(xù)函數(shù).

(H12) 存在一個(gè)正數(shù)M>0, 使得

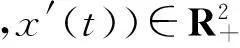
則在[0,1]上，邊值問(wèn)題(1)至少存在一個(gè)解.

證應(yīng)用Schauder’s不動(dòng)點(diǎn)定理來(lái)證明由式(4)定義的算子T在[0,1]上有一個(gè)不動(dòng)點(diǎn).

首先,設(shè){xn}是一個(gè)序列,并且在C1([0,1],R+)上xn→x.則?t∈[0,1]有：

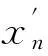
因?yàn)閒是連續(xù)函數(shù)并且由引理2，有：

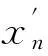
即 ‖T(xn)-T(x)‖→0,當(dāng)n→∞時(shí).因此，T是一個(gè)連續(xù)算子.

其次，任給η*>0，令Bη*={x∈C1([0,1],R+):‖x‖≤η*}，易知Bη*是有界凸閉集.?x∈Bη*， 證明存在一個(gè)正數(shù)l使得‖T(x)‖≤l.

事實(shí)上，?t∈[0,1]，由引理2，(4)式和條件(H12) 有：

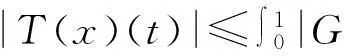
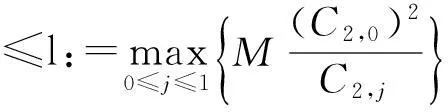
下面證明,T是C1([0,1],R+)上全連續(xù)算子.

令t1,t2∈[0,1],t1

則當(dāng)t1→t2時(shí)，上面不等式的右邊趨于零.由Arzela’-Ascoli定理得知T是全連續(xù)的算子.

因此算子T在[0,1]上滿足Schauder’s不動(dòng)點(diǎn)定理，即邊值問(wèn)題(1)至少存在一個(gè)解.

在定理4中，如果將條件(H12)減弱的話，還可以得到更一般的存在性結(jié)果(見文獻(xiàn)[1]).

(H13) 存在一個(gè)泛函φf(shuō)∈L1([0,1],R+)和一個(gè)連續(xù)非減函數(shù)φ:[0,∞)→(0,∞)，使得

(H14) 存在一個(gè)正數(shù)K>0,使得

則在[0,1]上，邊值問(wèn)題(1)至少存在一個(gè)解.

證對(duì)于由(4)式定義的算子T，考慮?λ∈[0,1],0≤t≤1，令x(t)滿足：x(t)=λ(Tx)(t)，則由式(H13)和式(H14)，有：

φ(‖x‖)[Iαφf(shuō)(t)+(1-t)(Iαφf(shuō)(1)+Iα-1φf(shuō)(1))]≤

φ(‖x‖)(‖Iαφf(shuō)‖L1+Iαφf(shuō)(1)+Iα-1φf(shuō)(1)).

3數(shù)值例子

例1考慮如下邊值問(wèn)題

(11)

則f(t;x(t),x′(t))是[0,1]上的連續(xù)函數(shù)，并且|f(t;x(t),x′(t))|≤2，由定理4知邊值問(wèn)題(11)在[0,1]上至少存在一個(gè)解.

例2考慮如下邊值問(wèn)題

(12)

Picard’s迭代序列前10項(xiàng)數(shù)值解x1(t),x2(t),x3(t),…,x10(t)和唯一解x*(t)如下表所示.

表1　數(shù)值解和唯一解

致謝感謝安徽大學(xué)鄭祖庥教授、中科院俞元洪研究員的教誨和指導(dǎo)!

參考文獻(xiàn)：

[1]AGARWAL R P, BENCHOHRA M, HAMANI S. Boundary value problems for fractional differential equations[J].J Georgian Math, 2009,16(3):401-411.

[2]BENCHOHRA M, HAMANI S, NTOUYAS S K. Boundary value problems for differential equations with fractional order[J]. Surv Math Appl, 2008,3(3):1-12.

[3]BENCHOHRA M, HAMANI S, NTOUYAS S K. Boundary value problems for differential equations with fractional order and nonlocal conditions[J]. Nonlinear Anal, 2009,71(5):2391-2396.

[4]ZHANG S Q. Positive solutions for boundary-value problems of nonlinear fractional differential equations[J]. Electron J Diff Equ, 2006,36(2):1-12.

[5]SUN Y F, WANG P G. Quasilinear iterative scheme for a fourth-order differential equation with retardation and anticipation[J]. Appl Math Comput, 2010,217(4):3442-3452.

[6]WANG P G. Iterative methods for the boundary value problem of a fourth order DDE[J]. Appl Math Comput, 1995,73(2):257-270.

[7]SUN Y F, WANG P G. Iterative methods for a fourth-order differential equations with retardation and anticipation[J]. Dyn Cont Disc Impuls Syst, Series B, 2010,17(1):487-500.

[8]PODLUBNY I. Fractional Differential equations[M]. New York: Academic Press, 1999.

[9]RALL L B. Computational Solutions of Nonlinear Operator[M]. New York:John Wiley,1969.

[10]GRANAS A, DUGUNDJI J. Fixed point theory[M].New York:Springer-Verlag,2003.

[11]SUN Y F, LI T S. Quasilinearization methods for a fourth-order differential difference equations[J]. J. Biomath, 2007,22(5):840-846.

[12]孫宇鋒.一類四階微分差分方程的邊值問(wèn)題[D].保定：河北大學(xué)碩士論文， 2008.

[13]鄭祖庥.分?jǐn)?shù)微分方程的發(fā)展和應(yīng)用[J].徐州師范大學(xué)學(xué)報(bào):自然科學(xué)版， 2008，26(2):1-10.

[14]薛定宇，陳陽(yáng)泉.高等應(yīng)用數(shù)學(xué)問(wèn)題的MATLAB 求解[M].北京：清華大學(xué)出版社， 2004.

[15]陳文，孫洪廣.力學(xué)與工程問(wèn)題的分?jǐn)?shù)階導(dǎo)數(shù)建模[M].北京：科學(xué)出版社，2010.

[16]程金發(fā).分?jǐn)?shù)階差分方程理論[M].廈門：廈門大學(xué)出版社，2011.

(編輯HWJ)

Picard’s Iterative Method for the Boundary Value Problem of a Class of the Fractional Order Differential Equation

SUNYu-feng*,ZENGGuang-zhao

(College of Mathematics and Statistics, Shaoguan University, Shaoguan 512005, China)

AbstractIn this article the existence and uniqueness of the solution for the boundary value problem of a class of fractional differential equations is proved by the Picard’s iterative method starting form the approximate solution of boundary value problems of these equations. We also proved the existence and uniqueners of the solution and provided the sufficient conditions for the boundary value problem by the Picard’s iterative methods when the nonlinear function f(t;x(t),x′(t)) is approximated instead of by a sequence of functions {fm(t;x(t),x′(t))}. The general condition for the existence of its solution is discussed without considering factors like the approximate solution of such boundary value problems and nonlinear function Lipschitz-class. Finally， the existence of the solution of such boundary value problems and the estimation of error between the accurate solution and the solution of iterative sequence are verified by two numerical examples.

Key wordsfractional differential equations; iterative method; approximate solution; estimation of error

中圖分類號(hào)O175.8，O241.81

文獻(xiàn)標(biāo)識(shí)碼A

文章編號(hào)1000-2537(2016)02-0082-08

*通訊作者,E-mail：surry2001@sina.com

基金項(xiàng)目：廣東省自然科學(xué)基金資助項(xiàng)目(S2012010010069)；中山大學(xué)廣東省計(jì)算科學(xué)重點(diǎn)實(shí)驗(yàn)室開放基金資助項(xiàng)目(201206015)；韶關(guān)市科技計(jì)劃基金資助項(xiàng)目(2011CX/K20)

收稿日期：2015-07-02

DOI:10.7612/j.issn.1000-2537.2016.02.014