集裝箱碼頭堆場出口箱箱區空間分配動態模型

嚴南南，崔景云

(上海海事大學 物流研究中心，上海 201306)

集裝箱碼頭堆場出口箱箱區空間分配動態模型

嚴南南，崔景云

(上海海事大學 物流研究中心，上海 201306)

針對集裝箱碼頭堆場箱區空間利用率不高的問題，考慮箱區貝位間作業量的平衡以及龍門吊的使用數量，采用作業量平衡的堆存策略，運用數學規劃方法建立模型，并對模型進行求解。實驗結果顯示該模型不僅能確定不同尺寸集裝箱分配到各箱區貝位中的具體數量，還能實現不同裝卸作業線上集裝箱的錯開堆放，有效地提高了堆場空間的利用率，同時提高了堆場裝卸作業效率。

交通運輸工程；集裝箱；箱位分配；動態模型；作業平衡

0 引 言

對港口空間資源利用要求較高的集裝箱碼頭而言，若集裝箱抵港后，沒有實施高效的堆場箱區空間分配策略，勢必會帶來嚴重的擁堵現象。一般規模的集裝箱港口堆場都配置有龍門吊，與橋吊、集卡協同作業[1]。堆場龍門吊用來裝卸、搬運和堆碼堆場集裝箱，可以在異箱區及同箱區異貝位之間來回移動，龍門吊的購買、維護與修理成本很高。在堆場作業過程中，若注重各時段各箱區貝位工作量的平衡性，不僅會減少龍門吊調度數量，還可保持龍門吊作業的穩定性，從而實現龍門吊的高效利用。

已經有大量國內外學者對堆場空間分配問題進行了研究。P.Preston等[2]在集裝箱裝船順序已知情況下，研究了出口集裝箱的堆存位置分配問題。但實際中，在出口集裝箱到達碼頭之前，通常無法獲知裝船順序。K.H.Kim等[3]運用混合整數規劃方法建立模型，從集卡運輸距離最小化和龍門吊移動距離最小化兩個方面進行了出口堆場空間分配問題的研究。K.H.Kim等[4]同時給出了集裝箱堆存高度和布置最優情況的獲得方法，即加權方法和擇箱指數方法。Jiang Xinjia等[5]提出相鄰箱區之間的空間共享方法，為船舶動態預留堆存空間，以實現堆存空間的高效利用。Lee Der-Hong等[6]綜合考慮港口船舶的泊位分配及中轉型集裝箱的堆場分配問題，采用整數規劃方法建立模型，并運用兩階段算法對模型進行求解。范靈芳等[7]同樣采用兩階段算法實現了集裝箱碼頭出口箱堆位分配問題的求解，算法中運用了混合整數規劃方法和基于混堆的啟發式算法。陶經輝等[8]針對集裝箱工作量平衡問題及箱區間平衡優化問題，建立了進出口集裝箱堆存的數學模型，并運用啟發式算法進行求解。嚴偉等[9]建立了滾動式計劃的出口堆場分配模型，減少了箱子堆存位置到泊位的水平運輸距離，也平衡了堆場內作業量，提高了裝船效率，降低了作業成本。

現有對堆場空間分配利用問題的研究中，大多考慮的是最小化集裝箱堆存于箱區的不均衡性和最小化集卡行駛總路程，較少涉及作業線情況和集裝箱尺寸的分類。在港口實際作業中，集裝箱尺寸一般分為20和40英尺。筆者結合港口實際作業情況建立集裝箱碼頭堆場箱區空間分配動態模型，平衡箱區貝位間作業量，合理分配作業線任務量，提高堆場箱區空間利用率。

1 問題描述

1.1 假設條件

集裝箱運輸行業迅猛發展，集裝箱船舶日益擴大的體積給碼頭作業帶來了新的挑戰。集裝箱碼頭堆場大部分工作量都是因船舶的抵達而產生。目前，碼頭集裝箱運輸基本采用班輪運輸模式[10]，班輪運輸的特點是時間、航線、裝箱港、卸箱港都是固定的，這樣便可以預知集裝箱船何時抵達目的港，預知船舶的進出口集裝箱箱量，方便制定詳細的堆場作業計劃。

港口集裝箱吞吐量巨增，必然帶來各作業線任務量的增加，翻箱問題不容忽略。為了減少甚至避免裝船作業的翻箱，一定要避免前期堆存作業中箱量分配的兩種極端情況，即相同作業線的集裝箱分散堆存多個箱區，不同作業線的集裝箱堆存同一箱區[11]。出口箱的堆存策略研究中，為了減少翻箱對堆存計劃的影響，堆放箱子過程中，要遵循一些堆放準則。如將同組箱分配到同一堆棧或同一堆存位、同尺寸按貝堆放、貝內不同船舶的集裝箱按先作業壓后作業方式堆放等[12]。另外，緩沖區的存在也有一定的爭議，如果不設立緩沖區，則會帶來堆場操作的減少，但是不能充分利用堆場空間。如果建立緩沖區，可以充分利用堆場空間，但無法避免翻箱作業[13]。筆者將不考慮緩沖區的存在，從而避免復雜的翻箱作業。圖1為集裝箱堆存作業示意。

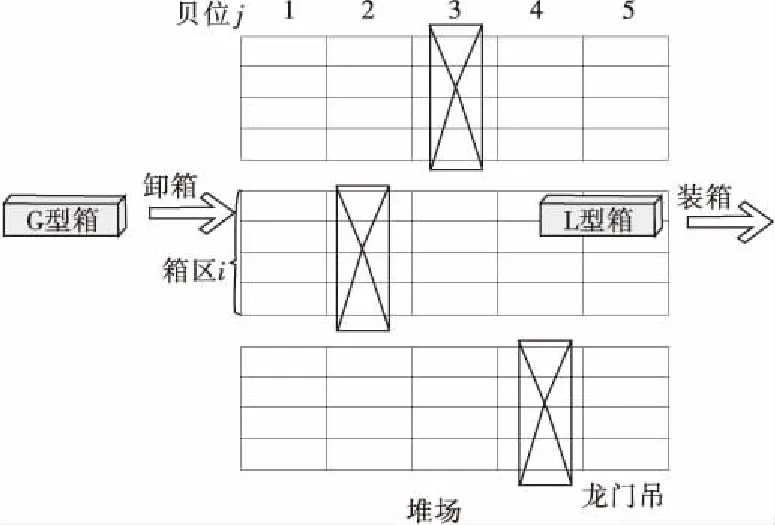
圖1 集裝箱堆存作業示意Fig.1 Schematic diagram of container storage

筆者研究的出口集裝箱堆場箱區空間分配問題涉及的箱區貝位有兩種：一種貝位只能堆存20英尺大小的集裝箱，另一種貝位(文中將其定義為大貝位)是由兩個連續貝位構成以堆存40英尺集裝箱，如貝位1，2可以稱為一個大貝位。此外，出口集裝箱要先進入堆場再離開，因此可將出口集裝箱分為兩類：①進箱(G)型出口集裝箱，即將要進入堆場進行堆存的出口集裝箱；②出口(L)型出口集裝箱：即將要離開堆場進行裝船的出口集裝箱。

出口集裝箱堆場箱區空間分配問題涉及的集裝箱總箱量由G型出口集裝箱和L型出口集裝箱的數量來決定。確定G型出口集裝箱具體要存放的箱區貝位，當G型出口箱堆存到堆場以后，就轉變成了L型出口集裝箱，L型出口集裝箱則按照分配的作業線離開堆場。可以看出，本期堆場存儲空間資源配置的決策不僅直接影響到龍門吊作業與G型集裝箱量，而且還會影響下一期作業的L型集裝箱量。因此需要將計劃周期分為若干階段，便于信息的實時更新。作業計劃一旦執行，后期出現的不確定信息就會對各級計劃產生影響，甚至影響整個計劃。為避免這種情況的發生，在執行完第一天的計劃后，及時獲取真實信息，制定新策略執行后期計劃。因此筆者采取滾動式計劃方法，計劃實施過程中，僅有第一時段的計劃被真正執行，之后要通過最新數據完成下一計劃周期計劃的制定，進行新一輪的計劃，這樣一直進行下去，見圖2[14]。

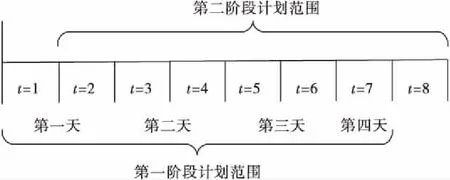
圖2 堆場滾動計劃Fig.2 Yard rolling plan

1.2 問題解決思路

考慮港口復雜的作業環境，筆者將堆場箱區空間動態分配問題按作業先后順序分解成兩個子階段問題，各階段都有相應的建模方法對問題進行求解。在第一階段，均衡化各個箱區貝位的作業箱量，將出口集裝箱按堆存準則平均堆存到各個箱區貝位中。在第二階段，考慮高低作業量因素，配置最少量的龍門吊，協同集卡，將出口集裝箱沿作業線裝船。一階段模型為箱區分配模型MD1，二階段模型為作業線分配模型MD2。

2 箱區分配模型MD1

MD1旨在保證各階段的進箱(G)型集裝箱平均堆存到各箱區各貝位，同時獲得每個階段每個箱區貝位所要作業的集裝箱具體數量。

2.1 模型假設

1)指定堆場箱區中某些貝位為大貝位，用來堆存40英尺集裝箱，也可堆存20英尺集裝箱；

2)可獲知確定的船期及其裝卸箱量；

3)只考慮計劃期內的工作。

2.2 模型參數

2.3 決策變量

Gijxt為在第t階段到達堆場，堆存到i箱區j貝位中的20英尺G型箱量，Gijyt為40英尺G型箱量；Gijxkt為在第t階段到達堆場，堆存到i箱區j貝位中，在(t+k)階段裝上船的20英尺G型箱量，Gijykt為40英尺G型箱量；Lijxt為堆存在i箱區j貝位中，在第t階段內被裝上船的20英尺L型箱量，Lijyt為40英尺L型箱量；Vijxt為第t階段開始時，已經堆存在i箱區j貝位的20英尺箱量，Vijyt為40英尺箱量；Nijxt在第t階段，i箱區j貝位作業的20英尺箱總箱量，Nijyt為40英尺箱總箱量。

2.4 數學模型MD1

目標函數為

(1)

約束條件為

(2)

(3)

(4)

(5)

Vijx(t+1)=Vijxt+Gijxt-Lijxt

(6)

Vijy(t+1)=Vijyt+Gijyt-Lijyt

(7)

Vijxt+2Vijyt≤Cij

(8)

(9)

目標函數(1)可求出每個階段，每個箱區貝位的作業箱量標準差之和，并進行最小化求解，即最大化各箱區貝位間作業箱量的均衡性。約束式(2)和式(3)確保在第t階段抵達碼頭，(t+k)階段裝船的20，40英尺出口集裝箱總箱量分別等于分配到各個箱區各個貝位中的20，40英尺出口集裝箱總箱量之和；約束式(4)和式(5)給出了在i箱區j貝位中，在第t階段裝船的L出口集裝箱的來源，一部分來自第t階段開始時堆場已堆存的出口集裝箱，另一部分來自在t階段前到達為止，在第t階段裝船的G型箱出口集裝箱。約束式(6)和式(7)確保箱區貝位前后總箱量一致性。約束式(8)保證堆場箱區貝位能夠滿足集裝箱的堆存。約束式(9)保證每個箱區得有足夠多的空的大貝位用來堆存40英尺集裝箱。

3 作業線分配模型MD2

通過箱區分配模型MD1的求解，可以獲得各個階段各個箱區貝位要裝船的箱量，即Lijxt和Lijyt，在MD2的模型中，這些量就可以作為已知量來使用。

3.1 模型假設

1)整個規劃期內，對規劃期內的任意一艘船舶，已在堆場為其指定裝載出口箱的貝位；

2)任意一個計劃期內，相鄰貝位不能同時進行集裝箱的裝載作業[15]；

3)一條作業線上的出口集裝箱最多是從兩個箱區中裝載；

4)一個箱區可配置的龍門吊最大數目為2。

3.2 模型參數

R為規劃期內船舶的作業線集合；M為很大的正數；Nij為i箱區j貝位的相鄰貝位j＇的集合；Xr為第r條作業線上需要裝載的20英尺出口集裝箱總量；Yr為第r條作業線上需要裝載的40英尺出口集裝箱總量；Vxb為b船舶在此港口計劃裝載的20英尺出口集裝箱總數量，Vyb為40英尺出口集裝箱總數量；A為龍門吊一個班次內的作業能力；MCi為配置給i箱區的龍門吊最大數；HL為高工作量的最低值；HU為高工作量的最高值；LL為低工作量的最低值；LU為低工作量的最高值；Zrt為在第t階段到達碼頭，經作業線r裝上船的進箱型總箱量。

3.3 決策變量

xijtr為在t階段到達碼頭，堆存在i箱區j貝位，經作業線r裝載走的20英尺箱量；yijtr為在t階段到達碼頭，堆存在i箱區j貝位，經作業線r裝載走的40英尺箱量；當i箱區j貝位處于高工作量時，hij=0；處于低工作量時，hij=1；若第r條作業線上的出口集裝箱是從i箱區裝載走的，alir=1，否則alir=0。

3.4 數學模型MD2

目標函數為：

(10)

約束條件為

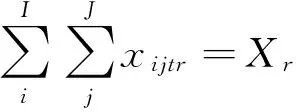
(11)

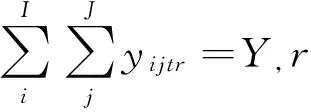
(12)

Xr+Yr=Zrt

(13)

(14)

(15)

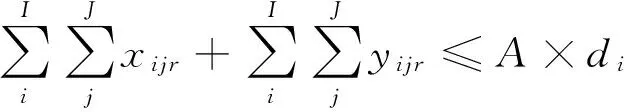
(16)

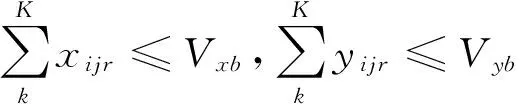
(17)

(18)

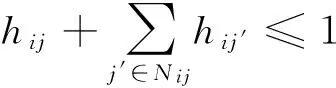
(19)

(HU-LU), ?i,j

(20)

xijr+yijr≤M·alir, ?i,j,r

(21)

xijr≥0,yijr≥0,i=1,2,…;j=0,1,2,…;r=1,2,…

(22)

模型MD2目標函數(10)旨在實現配置給堆場箱區的龍門吊數目合理化、最小化。約束式(11)表示裝載走的20英尺中轉集裝箱總數要與裝載到船舶上的20英尺集裝箱總數一致。約束式(12)表示裝載走的40英尺中轉集裝箱總數要與裝載到船舶上的40英尺集裝箱總數一致。約束式(13)表示t階段，經由作業路r的集裝箱總數前后保持一致。約束式(14)和式(15)是箱區貝位作業箱量的限制。約束式(16)確保箱區配置的龍門吊有能力完成所有工作量。約束式(17)給出了船舶在此港口計劃裝載的不同類型集裝箱的數量。約束式(18)給出箱區可調動的龍門吊數量限制。考慮高低工作量平衡模式，約束式(19)確保高工作量作業不能同時發生在相鄰貝位，約束式(20)考慮了龍門吊工作率，任意一個貝位的作業量要適當，避免過高過低。如果相鄰貝位作業量恰好一個處于高工作量模式，一個處于低工作量模式，則可共用一龍門吊。倘若幾個連續貝位都處于低工作量模式，可共用同一龍門吊[16]。約束式(21)是判斷第r條作業線上裝載的集裝箱是否來自i箱區。約束式(22)是非負整數約束。

4 計算實驗

4.1 已知數據及條件假設

本模型設定3天的計劃期，為了及時獲取準確的信息，實例計算中采用第一天的結果來制定后期策略，即本實例計劃期天數為1，T取值為6。箱區作業由輪胎式龍門吊完成，箱區數量B為4，每個箱區有5個貝位，6列寬，5層高，其中第4貝位堆存的是40英尺集裝箱，其他貝位堆存的都是20英尺集裝箱，每個貝位的最大堆存能力Cij為30。第一階段中堆場箱區初始堆存量Vij1是已知的，其中1箱區貝位1到6的初始堆存箱量為(15,9,17,21,19,15)，2箱區相應初始堆存箱量為(17,24,23,25,24,21)，3箱區相應初始堆存箱量為(23,20,24,10,28,26)，4箱區貝位1到6相應堆存箱量為(25,27,28,26,22,19)。

第二階段選取兩個班次進行分析，一個班次內，龍門吊的作業能力A為100，作業線R為3，每個作業線的集裝箱量最大為260，HU=100，HL=70，LU=50，LL=0。部分已知變量數值見表1～表3。

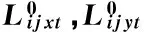
表1 箱量Table 1 Container quantity

注：例如表1中(2,0,1,5,3,4)表示計劃階段初始時，箱區1貝位1到6里，計劃在t=1時的裝船箱量分別為 2，0，1，5，3，4；其中計劃裝在第4貝位的是5個40英尺集裝箱。

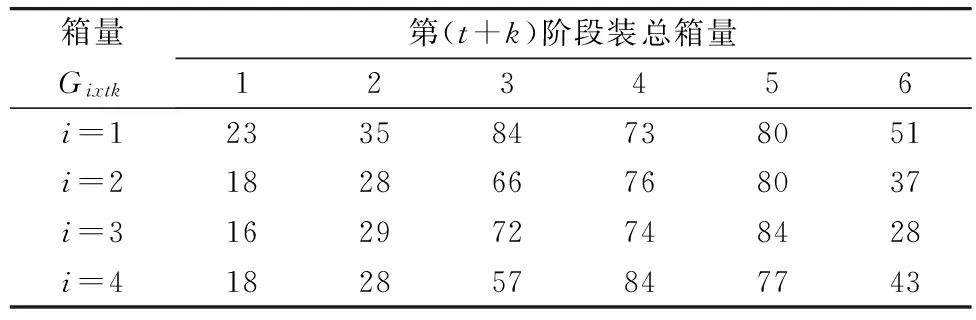
表2 箱量GixtkTable 2 Container quantity Gixtk

注：例如表2中23表示第(t+k)階段裝上船的20英尺集裝箱總箱量。

表3 箱量GiytkTable 3 Container quantity Giytk

(續表3)

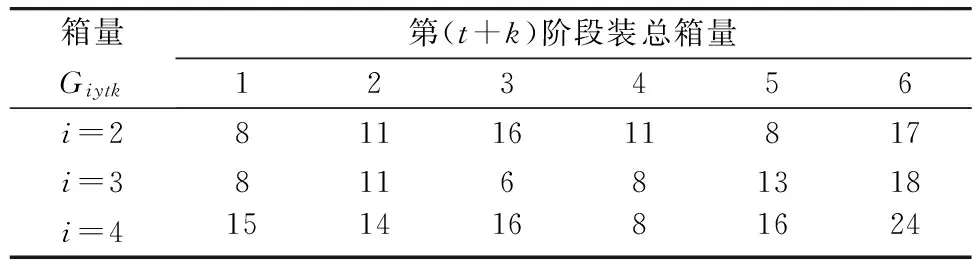
箱量Giytk第(t+k)階段裝總箱量123456i=28111611817i=3811681318i=415141681624

注：例如表3中8表示第(t+k)階段裝上船的40英尺集裝箱總箱量。

4.2 執行結果分析

根據箱區分配模型MD1和作業線分配模型MD2，運用Lingo算法對上述算例進行求解。

在t階段到達碼頭堆場，存放到i箱區j貝位，將要裝船的集裝箱箱量Lijt見表4。

表4 箱量 LijtTable 4 Container quantity Lijt

注：例如表4中(9,0,4,13,9,11)表示箱區1貝位1到6里，在t=1時，要裝船的箱量分別為9,0,4,13,9,11；

從表4中選取t=2，5作為班次1，班次2進行分析求解，結果見表5和表6。

表5 班次1作業線分配Table 5 The line distribution of frequency 1

注：例如表5中15(1)表示班次1作業線1的作業量是16。

表6 班次2作業線分配Table 6 The line distribution of frequency 2

注：例如表6中22(1)表示班次2作業線1的作業量是22。

箱區分配模型MD1求出的標準差之和最小值為6.32，表示總的不平衡度，由于T取值為6，故每個階段的不平衡度值為1.05，可見MD1可以最大化各箱區貝位間作業箱量的均衡性。

作業線分配模型MD2可計算出集裝箱作業線分配情況，表5中可看出R1箱量為81，R2箱量為81，R3箱量為83，表6中R1箱量為152，R2箱量為150，R3箱量為153，每條作業線最多分配到兩個箱區，而且每條作業線上的集裝箱總量差別不大，這樣就避免了集卡在各個箱區移動造成擁堵現象。模型中規定一個箱區龍門吊數量最多為2個，如果不限制箱區龍門吊的配置數量，就會分散化集裝箱的作業線分配，便會導致龍門吊移動次數的增加。龍門吊移動次數過多，不僅會減少龍門吊設備的使用時間，還會導致計劃作業無法按時完成，進而需要配置更多的龍門吊來完成作業，無法實現合理配置，與實際情況不符合。

5 結 語

筆者對出口集裝箱堆場箱區空間動態分配問題進行了研究。結合滾動計劃方法，任意一個計劃期里，按照碼頭作業順序，都從兩個子問題進行考慮，一是分配箱區進行不同尺寸集裝箱堆存作業，二是分配作業線進行不同尺寸集裝箱裝船作業。將每個子問題抽象成數學規劃模型，即箱區分配模型MD1和作業線分配模型MD2。MD1旨在均衡各箱區貝位的箱量，同時針對不同尺寸集裝箱制定不同的堆存計劃，MD2確保完成任務的龍門吊使用數量最少，也保證了不同作業線作業箱量的均衡性。模型將箱區分配和作業線分配有序合理地結合，可以得到不同尺寸集裝箱在堆場箱區的具體堆存貝位及數量，對出口集裝箱堆場箱區空間動態分配問題是可行的。

但是堆場空間分配問題是一個復雜的多目標多約束問題。算例分析中，小規模的問題可以用lingo軟件進行求解，大規模的問題則需要考慮智能算法。在未來的研究中，將考慮堆場箱區的翻箱作業，同時增加其他目標或約束條件，利用智能算法對復雜問題進行求解與優化。

致謝：本論文得到上海海事大學基金項目“現代港口供應鏈管理智能決策支持關鍵技術研究”的支持，同時也非常感謝上海港務集團對本論文的研究所提供的支持。

[1] 王斌,徐國平.中轉港口堆場集裝箱堆存多目標優化模型[J].重慶交通大學學報(自然科學版),2013,32(6):1275-1278. WANG Bin,XU Guoping.Multi-objective optimization model of containers stacking in transshipment port yard[J].JournalofChongqingJiaotongUniversity(NaturalScience),2013,32(6):1275- 1278.

[2] PRESTON P,KOZAN E.An approach to determine storage locations of containers at seaport terminals[J].Computers&OperationsResearch,2001,28(10):983-995.

[3] KIM K H,PARK K T.A note on a dynamic space-allocation method for outbound containers[J].EuropeanJournalofOperationalResearch,2003,148(1):92-101.

[4] KIM K H,PARK Y M,RYU K R.Deriving decision rules to locate export containers in container yards [J].EuropeanJournalofOperationalResearch,2000,124(2):89-101.

[5] JIANG Xinjia,LEE L H,CHEW E P,et al.A container yard storage strategy for improving land utilization and operation efficiency in a transshipment hub port[J].EuropeanJournalofOperationalResearch,2012,221(1):64-73.

[6] LEE Der-Hong,JIN Jiangang,CHEN Jianghang.Terminal and yard allocation problem for a container transshipment hub [J].TransportationResearchPartE:LogisticsandTransportationReview,2012,48:516- 528.

[7] 范靈芳,陳璐.集裝箱碼頭出口箱堆位分配算法[J].系統工程，2011,29(10):80-85. FAN Lingfang,CHEN Lu.An algorithm for the storage location assignment problem for outbound containers in a container terminal[J].SystemEngineering,2011,29(10):80-85.

[8] 陶經輝,汪敏.基于混堆模式的集裝箱堆場區段分配[J].系統工程理論與實踐,2009,29(8):185-192. TAO Jinghui,WANG Min.Assign problem of container yard section based on mixed storage model[J].SystemsEngineering—Theroy&Practice,2009,29(8):185-192.

[9] 嚴偉,謝塵,萇道方.基于并行遺傳算法的集裝箱碼頭堆場分配策略[J].上海海事大學學報,2009,30(2):14-19. YAN Wei,XIE Chen,CHANG Daofang.Yard allocation strategy for container terminals based on parallel genetic algorithm[J].JournalofShanghaiMaritimeUniversity,2009,30(2):14-19.

[10] 衛家駿.出口集裝箱堆場位置的優化[J].重慶交通大學學報(自然科學版),2010,29(3):470-473. WEI Jiajun.Optimization of positioning export containers I in yard [J].JournalofChongqingJiaotongUniversity(NaturalScience),2010,29(3):470-473.

[11] YAN Nannan,ZHOU Yuan.Agent-based automatic shore operating scheduling for a container terminal[J].Telkomnika-IndonesianJournalofElectricalEngineering,2013,11(2):653-658.

[12] FOTUHI F,HUYNH N,VIDAL J M,et al.Modeling yard crane operators as reinforcement learning agents[J].ResearchinTransportationEconomics,2013,42(1):3-12.

[13] 徐亞,陳秋雙,龍磊,等.基于多目標規劃的堆場空間分配問題研究[J].系統工程學報,2009,24(3):365-369. XU Ya,CHEN Qiushuang,LONG Lei,et al.Yard space allocation based on multi-objective programming[J].JounalofSystemsEngineering,2009,24(3):365-369.

[14] 李斌,楊家其.面向負載均衡的集裝箱碼頭生產調度決策[J].系統仿真學報,2013,25(9):2222-2229. LI Bin,YANG Jiaqi.Modeling and simulation of logistics service scheduling at container terminals with framework of load balancing[J].JournalofSystemSimulation,2013,25(9):2222-2229.

[15] 鄭紅星,杜亮,董鍵.混堆模式下集裝箱堆場箱位指派優化模型[J].武漢理工大學學報(交通運輸系統工程與信息版),2012,12(1):153-159. ZHENG Hongxing,DU Liang,DONG Jian.Optimization method of container storage space allocation based on mixture storage[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering),2012,12(1):153-159.

[16] 王力,朱曉寧,謝征宇,等.基于混堆的鐵路集裝箱中心站堆場箱位指派模型[J].中南大學學報(自然科學版),2013,44(1):271-275. WANG Li,ZHU Xiaoning,XIE Zhengyu,et al.Container allocation optimization model of railway container terminal yard based on mixed storage[J].JournalofCentralSouthUniversity(ScienceandTechnology),2013,44(1):271-275.

Dynamic Model of Block Space Allocation on Container Terminal Yard

YAN Nannan, CUI Jingyun

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, P. R. China)

Aiming at the problem of low utilization of container area of storage yard on container terminal, the dynamic space deployment model was set up for solution by using the mathematics planning method, considering the balanced workload between adjacent bays and the number of gantry carne involved and adoption of storage strategy for workload balance. The running results demonstrate that this model can not only determine the actual numbers of the different-sized containers assigned to each bay but also achieve the staggered stacking of containers on different loading and unloading lines thus effectively improving space utilization of storage yard meanwhile improving the loading and unloading efficiency.

traffic transportation engineering; container; block space allocation; dynamic model; workload balance

10.3969/j.issn.1674-0696.2016.02.33

2014-10-17；

2014-12-03

現代港口供應鏈管理智能決策支持關鍵技術研究(20100068)

嚴南南(1968—)，女，湖北鄂州人，副教授，博士，主要從事智能信息處理、物流系統優化方面的研究。E-mail:nnyan68@163.com。

崔景云(1991—)，女，河南駐馬店人，碩士研究生，主要從事物流工程管理方面的研究。E-mail:jingyuncui2013@163.com。

U691.3

A

1674-0696(2016)02-163-06