面向多視角數(shù)據(jù)的極大熵聚類算法*

張丹丹，鄧趙紅，王士同

江南大學數(shù)字媒體學院，江蘇無錫214122

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(04)-0554-11

?

面向多視角數(shù)據(jù)的極大熵聚類算法*

張丹丹+，鄧趙紅，王士同

江南大學數(shù)字媒體學院，江蘇無錫214122

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(04)-0554-11

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel: +86-10-89056056

* The National Natural Science Foundation of China under Grant No. 61170122 (國家自然科學基金); the New Century Excellent Talent Foundation from MOE of China under Grant No. NCET-12-0882 (教育部新世紀優(yōu)秀人才支持計劃).

Received 2015-05,Accepted 2015-07.

CNKI網(wǎng)絡(luò)優(yōu)先出版: 2015-08-11, http://www.cnki.net/kcms/detail/11.5602.TP.20150811.1519.004.html

摘要：當前，極大熵聚類（maximum entropy clustering，MEC）在面對多視角聚類任務(wù)時，是將多視角樣本合并成為一個整體樣本再進行處理，然而這樣會破壞各視角的獨立性特征，進而影響最終的劃分結(jié)果。針對該問題，首先提出多視角協(xié)同劃分極大熵聚類算法（multi-view collaborative partition MEC，CoMEC），該算法加book=555,ebook=109入一個協(xié)調(diào)各視角空間劃分的約束項，使得每一視角在單獨聚類過程中考慮到其他視角的影響；然后通過區(qū)分每個視角的重要性將CoMEC算法擴展為視角加權(quán)版本，即視角加權(quán)協(xié)同劃分極大熵聚類算法（view weighted collaborative partition MEC，W-CoMEC）；最后利用幾何均值的集成策略得到全局性的劃分結(jié)果。在人工數(shù)據(jù)集以及UCI數(shù)據(jù)集上的實驗結(jié)果均顯示所提算法較之已有的聚類技術(shù)在應(yīng)對多視角聚類任務(wù)時具有更好的聚類性能。

關(guān)鍵詞：熵；多視角聚類；劃分；權(quán)值；集成策略；UCI數(shù)據(jù)集

1　引言

眾所周知，聚類的目的是將對象或數(shù)據(jù)樣本劃分為組或類，而在相同組或類的對象或數(shù)據(jù)樣本相對具有相似性，不同組或類的對象或數(shù)據(jù)樣本則相對具有不相似性。聚類作為一種無監(jiān)督學習技術(shù)，是數(shù)據(jù)挖掘、模式識別等領(lǐng)域的重要研究內(nèi)容之一，在識別數(shù)據(jù)的內(nèi)在結(jié)構(gòu)方面具有極其重要的作用。然而，由于現(xiàn)代技術(shù)的發(fā)展，數(shù)據(jù)復(fù)雜性隨之不斷提高，使得聚類算法的研究面臨更大的挑戰(zhàn)。

當前，人們對經(jīng)典的聚類分析方法的研究不斷深入，其中經(jīng)典的極大熵聚類（maximum entropy clustering，MEC）算法[1]已成為眾人研究的重點，相關(guān)文獻[2-5]給出了很多有關(guān)MEC算法的研究成果。由于數(shù)據(jù)復(fù)雜性提高，人們在觀察復(fù)雜數(shù)據(jù)集時，往往可以通過多個視角來詮釋，即得到多視角數(shù)據(jù)。多視角數(shù)據(jù)是指一些事物或?qū)ο髲牟煌瑢傩钥臻g有多個視角或特征組，它是從不同角度綜合多種類型屬性特征的結(jié)果。例如一個銀行客戶數(shù)據(jù)集，可以被分為表示客戶的人口信息的人口統(tǒng)計視角、顯示有關(guān)客戶賬戶信息的賬戶視角和描述客戶消費行為的消費視角。多視角聚類算法的研究也成為當前研究的重點。研究表明，極大熵聚類算法主要是針對單一視角數(shù)據(jù)的聚類方法，該算法在面對多視角聚類任務(wù)時，只能單獨對每一個視角進行獨立聚類分析以獲取各視角下的聚類結(jié)果，然后使用集成學習機制[6-7]將每一視角下的聚類結(jié)果進行統(tǒng)一，最終得到全局意義下的聚類結(jié)果。但是，人為地把多視角數(shù)據(jù)分解為多個單一視角數(shù)據(jù)進行處理，會因各個視角的聚類結(jié)果存在明顯差異而給最終獲取的全局聚類結(jié)果帶來不好的影響，使得最終的全局聚類結(jié)果出現(xiàn)惡化，最終造成算法性能較差或不穩(wěn)定。對此，本文提出對各視角共性和差異性綜合考慮的新方法，首先通過協(xié)同劃分學習參數(shù)協(xié)調(diào)各個視角的空間劃分，提出多視角協(xié)同劃分極大熵聚類算法（multiview collaborative partition MEC，CoMEC）；繼而，通過給每個視角添加權(quán)值，表示不同視角的重要性程度，以達到更好的聚類性能，提出增強版本算法，即視角加權(quán)協(xié)同劃分極大熵聚類算法（view weighted collaborative partition MEC，W-CoMEC）。

當前，針對多視角數(shù)據(jù)的聚類問題，相關(guān)的可利用聚類技術(shù)包括如下幾個方面的進展。

首先，基于多視角學習技術(shù)的聚類方法近年來受到廣泛的關(guān)注。如文獻[8]提出了可用于解決多視角聚類問題的協(xié)同聚類算法Co-EM（collaborative EM）。同樣文獻[9]基于協(xié)同思想提出了一種雙視角譜聚類算法。文獻[10]利用圖論的知識提出了多視角譜聚類算法。此外，文獻[11]首次在經(jīng)典的模糊C均值（fuzzy C-means，F(xiàn)CM）算法中采用協(xié)同聚類的思想，提出了CoFC（collaborative fuzzy clustering）算法。文獻[12]同樣基于FCM算法提出多視角模糊聚類算法Co-FKM（collaborative fuzzy K-means），相關(guān)文獻的實驗表明Co-FKM算法較之一些相關(guān)多視角算法具有一定的優(yōu)勢。此外，文獻[13]以經(jīng)典的K-means算法為框架，提出了一種多視角K-means聚類方法，即多視角雙層變量自動加權(quán)聚類算法TWKM （TW-K-means），該文獻的實驗展現(xiàn)出TWKM算法處理多視角聚類任務(wù)的良好性能。

此外，針對多視角數(shù)據(jù)的聚類問題，相關(guān)的聚類技術(shù)還有多任務(wù)聚類技術(shù)、組合聚類技術(shù)及基于樣本與特征空間的協(xié)同聚類技術(shù)。如文獻[14]的LSSMTC（learning the shared subspace for multi-task clustering）算法是一個典型的應(yīng)用多任務(wù)聚類技術(shù)的算法。該算法把各視角看作一個單一聚類任務(wù)，且考慮的是任務(wù)之間的相似性，不同任務(wù)對應(yīng)不同的聚類對象；另外，該算法要求每個視角的數(shù)據(jù)樣本特征數(shù)相等，即其不能處理各視角樣本特性數(shù)不等的多視角聚類任務(wù)。文獻[14]中的組合K-means （CombKM）算法則是采用組合聚類技術(shù)的思想，在處理多視角數(shù)據(jù)時，將不同視角下的樣本特征組合為一個整體進行處理，這種做法破壞了各視角間的獨立性，進而影響最終的聚類結(jié)果。文獻[15]基于樣本與特征空間的協(xié)同聚類技術(shù)提出了Co-clustering （collaborative clustering）算法。該算法在處理多視角聚類任務(wù)時，不僅采用組合聚類思想對樣本進行聚類，同時還考慮了對特征的劃分。然而由于其采用了與組合聚類相同的思想，使得其對特征空間的劃分相對粗糙，最終的聚類結(jié)果不理想。

本文組織結(jié)構(gòu)如下：第2章簡要介紹了MEC算法；第3章提出了一種多視角協(xié)同劃分極大熵聚類算法；第4章提出了增強的版本，即視角加權(quán)協(xié)同劃分極大熵聚類算法；第5章分別在人工模擬數(shù)據(jù)集和UCI真實數(shù)據(jù)集上驗證了所提算法的性能，并與相關(guān)算法進行了比較；第6章總結(jié)全文。

2　極大熵聚類算法

對于樣本集X={x1,x2,...,xn}，根據(jù)某種相似性測量，它被聚類成c(2≤c≤n)個子類，各類中心用矩陣Z=[z1,z2,…,zc]表示；劃分可用矩陣U=[uij]∈Rcn表示，其中每一項滿足如下的約束：

極大熵聚類算法的目標函數(shù)定義為：

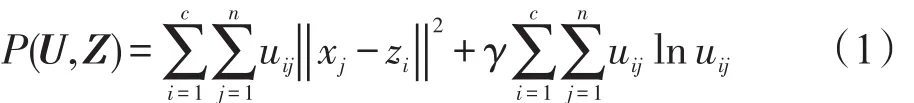
這里‖°‖表示歐幾里德距離；參數(shù)γ是非負常數(shù)。對于目標函數(shù)（1），利用拉格朗日極值求解方法，得到類中心及劃分矩陣的優(yōu)化迭代公式，如定理1所示。

定理1 P(U, Z)取極小值的必要條件為：

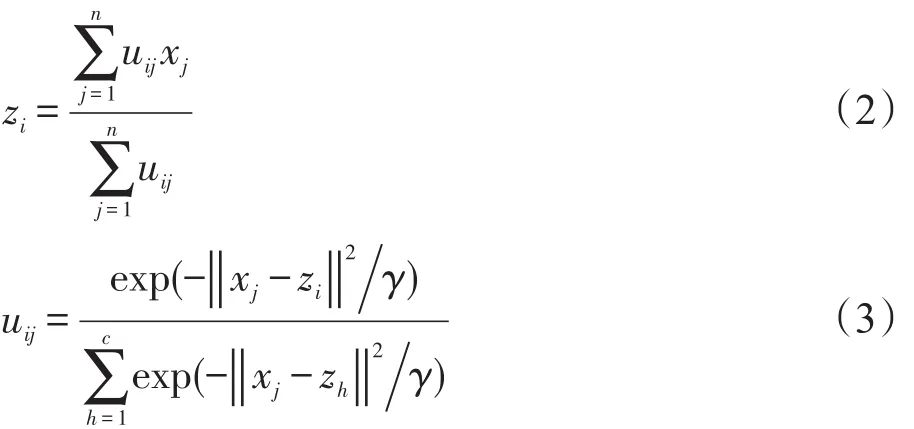
式中，i=1,2,…,c, j=1,2,…,n

根據(jù)定理1，極大熵聚類算法可描述如下：

算法1極大熵聚類算法

輸入：樣本集X={x1,x2,…,xn}，聚類類別c(2≤c≤n)，迭代閾值ε，迭代次數(shù)r，參數(shù)γ。

輸出：全局性的模糊劃分矩陣U，聚類中心矩陣Z。

步驟1初始化劃分矩陣U(0)；

步驟2根據(jù)式（2）更新類中心Z(r)；

步驟3根據(jù)式（3）更新隸屬度U(r)為U(r+1)；

步驟4若‖U(r+1)-U(r)‖F(xiàn)≤ε，則算法迭代循環(huán)停止，否則返回步驟2。

上述算法中‖°‖F(xiàn)表示Frobenius范數(shù)。極大熵聚類算法是針對單一視角數(shù)據(jù)的經(jīng)典算法，在面向多視角數(shù)據(jù)時，采用與處理單一視角數(shù)據(jù)相同的思想處理多視角數(shù)據(jù)，這極大地影響了極大熵聚類算法的性能。針對此問題，本文首先提出了一個面向多視角數(shù)據(jù)的聚類算法，即多視角協(xié)同劃分極大熵聚類算法。

3　多視角協(xié)同劃分極大熵聚類算法

3.1改進的目標函數(shù)

根據(jù)上文對極大熵聚類算法面對多視角聚類任務(wù)的局限性分析，本文首先提出了一種多視角極大熵聚類算法，即多視角協(xié)同劃分極大熵聚類算法。

對于一個有k個視角的多視角樣本集X={view1, view2,…,viewk}，其第k個視角的樣本集可表示為viewk={x1,k,x2,k,…,xN,k}。對該多視角數(shù)據(jù)樣本進行聚類時，根據(jù)某種相似性度量，把每一視角聚類為c(2≤c≤n)類，用矩陣Uk=[uij,k]表示第k個視角的劃分隸屬度，第k個視角的聚類中心可用矩陣Zk=[z1,k, z2,k,…,zc,k]表示。則多視角協(xié)同劃分極大熵聚類算法的目標函數(shù)可表示如下：

對于目標函數(shù)（4）滿足如下約束條件：

這里‖°‖表示歐幾里得距離。式（5）中參數(shù)λ為協(xié)同學習參數(shù)，用來調(diào)控中各視角間協(xié)同學習的程度。參數(shù)γ、λ為非負常數(shù)。

最后，根據(jù)獲取的各視角的劃分，利用如下的集成方法得到最終具備全局特性的空間劃分矩陣：

3.2目標函數(shù)的優(yōu)化

對于目標函數(shù)（4），如下定理成立：

定理2當U固定時，P(U,Z)取得極小值的必要條件為：

定理3當Z固定時，P(U,Z)取極小值的必要條件為：

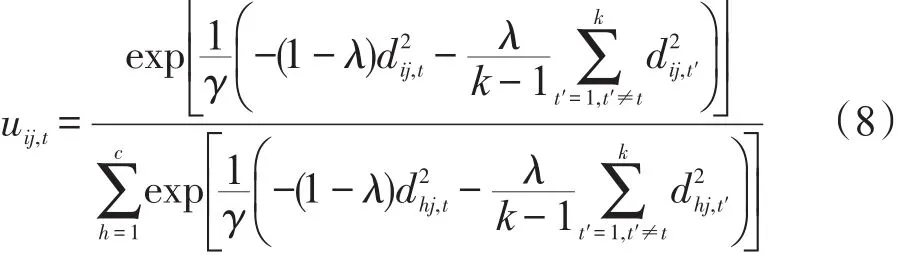
分別對uij,t,χ求導(dǎo)，并使得導(dǎo)數(shù)為0，得到：

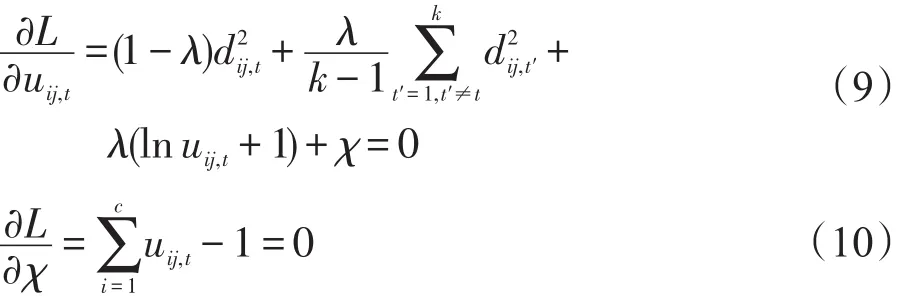
由式（9）和式（10）即可得到：

3.3算法描述

根據(jù)上節(jié)推導(dǎo)出的參數(shù)學習規(guī)則，給出算法的具體步驟如下：

算法2多視角協(xié)同劃分極大熵聚類算法

輸入：多視角樣本集X={view1,view2,…,viewk}共k個視角，其中viewk={x1,k,x2,k,…,xn,k}，聚類類別c(2≤c≤n)，迭代閾值ε，迭代次數(shù)l，參數(shù)λ、γ。

輸出：全局性的模糊劃分矩陣Uˉ，各視角聚類中心點Zi,k。

步驟1隨機產(chǎn)生各視角的模糊隸屬度uij,t(1≤t≤k)；

步驟2根據(jù)式（7）更新各視角下的中心點Zi,k；

步驟3根據(jù)式（8）更新各視角下的隸屬度uij,t；

步驟5算法收斂后，得到各視角下的隸屬度；

步驟6根據(jù)步驟5所獲取的各視角下的隸屬度uij,t，利用式（6）獲取具備全局特性的空間劃分矩陣Uˉ。

4　視角加權(quán)協(xié)同劃分極大熵聚類算法

本文在多視角協(xié)同劃分極大熵聚類算法的基礎(chǔ)上，提出了一個增強版本的聚類算法。該算法在處理多視角聚類任務(wù)時，不僅考慮了各視角的協(xié)同劃分，而且通過給每個視角添加一個表示其重要性程度的權(quán)值，使得不同視角達到更好的協(xié)調(diào)聚類性能。

4.1視角加權(quán)協(xié)同劃分極大熵聚類算法

根據(jù)以上對視角加權(quán)協(xié)同劃分極大熵聚類算法的介紹，其目標函數(shù)可表示如下：

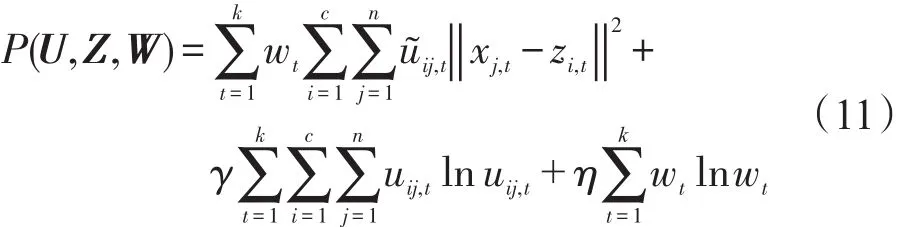
上式滿足如下約束：

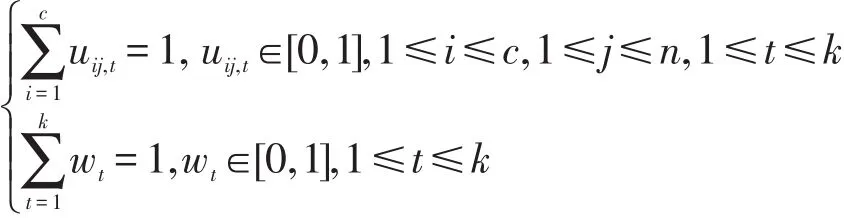
其中，W=[wk]是分配給各個視角的權(quán)重矩陣，它的每個元素表示對應(yīng)視角的重要性程度；是協(xié)同劃分項，其表示如式（5）所示；參數(shù)γ、η、λ為非負常數(shù)。

香農(nóng)熵正則化項在自適應(yīng)調(diào)整權(quán)值方面的有效性在相關(guān)文獻已得到充分的體現(xiàn)，例如在本文研究的極大熵聚類的概率劃分方面的成功應(yīng)用。為了確保視角W的協(xié)同劃分，式（11）引入了香農(nóng)熵正則化項，這使得在多視角聚類過程中各視角的權(quán)值得到更好的協(xié)調(diào)，進而得到更佳的視角劃分結(jié)果。

最后，類似于多視角協(xié)同劃分極大熵聚類算法，其增強方法根據(jù)獲取的各視角的劃分，同樣利用幾何均值的集成方法得到最終具備全局特性的空間劃分矩陣，具體見式（6）。

4.2目標函數(shù)的優(yōu)化

對于目標函數(shù)（11），如下定理成立：

定理4當U、W固定時，P(U,Z,W)取得極小值的必要條件為：

定理5當Z、W固定時，P(U,Z,W)取極小值的必要條件為：

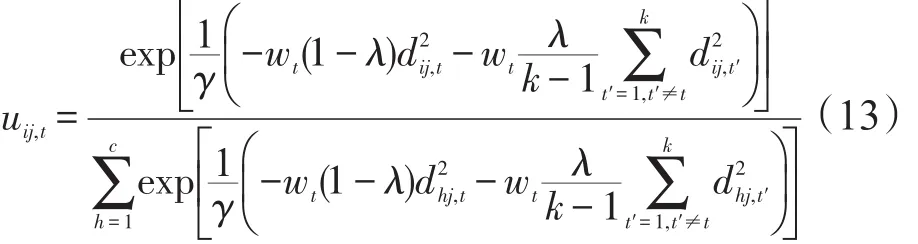
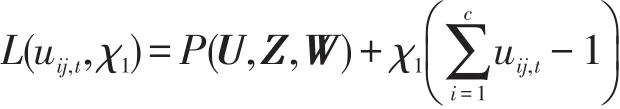
上式分別對uij,t,χ1求導(dǎo)，并使得導(dǎo)數(shù)為0，得到：

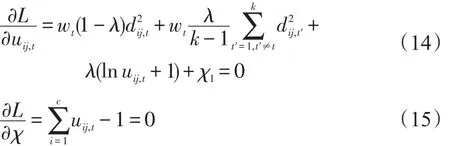
由式（14）和式（15）即可得到：

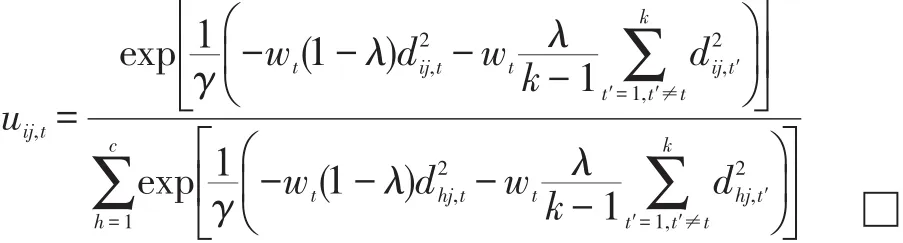
定理6當U、Z固定時，P(U,Z,W)取極小值的必要條件為：

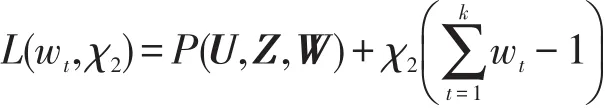
上式分別對wt、χ2求導(dǎo)，并使得導(dǎo)數(shù)為0，得到：

由式（17）和式（18）即可得到：

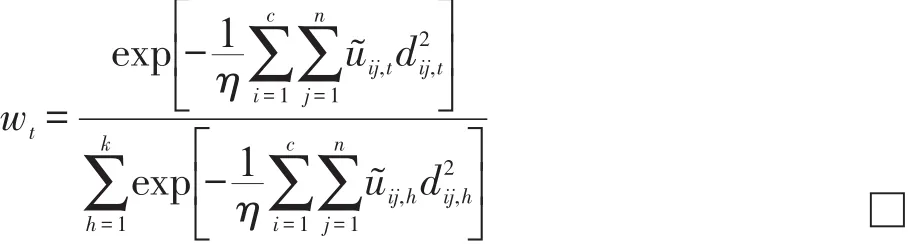
4.3算法描述

根據(jù)上節(jié)推導(dǎo)出的參數(shù)學習規(guī)則，下面給出增強版本W(wǎng)-CoMEC算法的具體步驟如下。

算法3視角加權(quán)協(xié)同劃分極大熵聚類算法

輸入：多視角樣本集X={view1,view2,…,viewk}共k個視角，其中viewk={x1,k,x2,k,…,xn,k}，聚類類別c(2≤c≤n)，迭代閾值ε，迭代次數(shù)l，參數(shù)γ、η、λ。

輸出：全局性的模糊劃分矩陣Uˉ，各視角聚類中心點Zi,k，視角權(quán)重矩陣W={wk}。

步驟1隨機產(chǎn)生各視角的模糊隸屬度uij,t(1≤t≤k)，隨機產(chǎn)生視角權(quán)重矩陣W={wk}；

步驟2根據(jù)式（12）更新各視角下的中心點Zi,k；

步驟3根據(jù)式（13）更新各視角下的隸屬度uij,t；

步驟4根據(jù)式（16）更新視角權(quán)重矩陣W={wk}；

步驟5如果‖Pl+1-Pl‖<ε，則算法迭代循環(huán)停止，否則跳回步驟2；

步驟6算法收斂后，得到各視角下的隸屬度；

步驟7根據(jù)步驟6所獲取的各視角下的隸屬度uij,t，利用式（6）獲取具備全局特性的空間劃分矩陣Uˉ。

4.4時間算法復(fù)雜度和收斂性分析

本節(jié)對算法的時間復(fù)雜度描述如下：對多視角協(xié)同劃分極大熵聚類算法，即CoMEC算法，其時間復(fù)雜度為O(tknc+tkc)；對其增強版本的視角加權(quán)協(xié)同劃分極大熵聚類算法，即W-CoMEC算法，由于該算法考慮到各視角的影響，故其時間復(fù)雜度為O(tk+ tknc+tkc)。其中t是算法迭代的總次數(shù)，k是數(shù)據(jù)集的視角個數(shù)，n是數(shù)據(jù)集的大小，c是類別數(shù)。由以上兩種算法的時間復(fù)雜度可知，考慮視角加權(quán)的WCoMEC算法和未考慮視角加權(quán)的CoMEC算法的時間復(fù)雜度數(shù)量級相差不大，具有相同的階次。

文獻[3]對MEC算法的收斂性已經(jīng)給出了收斂性分析，而根據(jù)相關(guān)收斂性理論[16-17]可知，W-CoMEC算法也是滿足Zangwill收斂性定理的條件的。

5　實驗研究

為了驗證本文算法處理多視角聚類任務(wù)的有效性，將分別對人工模擬數(shù)據(jù)集以及UCI標準多視角數(shù)據(jù)[18]進行實驗分析與評估。有關(guān)模擬數(shù)據(jù)集與真實數(shù)據(jù)集的詳細內(nèi)容將分別于下文給出，相關(guān)UCI標準多視角數(shù)據(jù)集的基本信息可見表1。為了對本文算法的聚類性能做出合理的判斷，也將給出與相關(guān)聚類算法的性能比較。實驗中采用的相關(guān)聚類算法有MEC算法[1]、多視角模糊聚類算法Co-FKM[12]、多視角雙層變量自動加權(quán)聚類算法TWKM[13]、基于多任務(wù)學習框架的LSSMTC算法[14]、基于多任務(wù)的組合K-means算法（CombKM）[14]及基于樣本與特征空間協(xié)同聚類的Co-clustering算法[15]。

另外，本文采用如下兩種常用的評價指標評估各聚類算法的聚類性能，即pairwise Precision[19]和NMI（normalized mutual information）[20-21]：

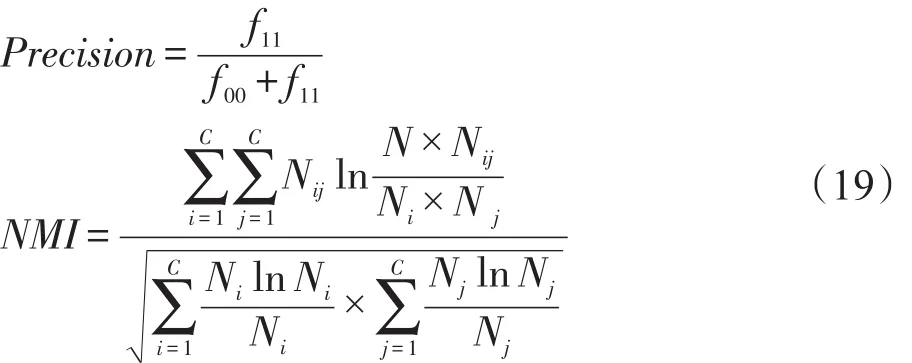
Table 1 Real multi-view UCI datasets表1　UCI真實多視角數(shù)據(jù)集

其中，f11表示數(shù)據(jù)點具有相同的類標簽并且屬于同一類的配對點數(shù)目，而f00則表示數(shù)據(jù)點具有不同的類標簽并且屬于不同類的配對點數(shù)目；Nij表示第i個聚類與類j的契合程度，Ni表示第i個聚類所包含的數(shù)據(jù)樣本量，Nj表示類j所包含的數(shù)據(jù)樣本量，而N表示整個數(shù)據(jù)樣本的總量大小。

以上兩種性能指標，其取值范圍均為[0, 1]，取值越接近1，表示算法的聚類性能越好。

本文所顯示的評價指標的均值和方差均為最優(yōu)參數(shù)下運行10次得到的。

5.1人工模擬數(shù)據(jù)集實驗

為了有效驗證本文算法的聚類性能，在人工模擬數(shù)據(jù)集實驗部分，針對UCI數(shù)據(jù)庫中真實數(shù)據(jù)集Iris，抽取其中三維特征，將每一維特征看作一個視角，進而構(gòu)造出具有3個視角樣本的多視角模擬數(shù)據(jù)集irisMoni。其中每個視角都由3類樣本組成，該數(shù)據(jù)集每個視角的具體信息如圖1所示。

Table 2 Definitions and settings of related notations表2　參數(shù)定義與設(shè)置

Fig.1 IrisMoni corresponding datasets under each view圖1　數(shù)據(jù)集IrisMoni各個視角樣本直觀圖

觀察圖1可以發(fā)現(xiàn)，在IrisMoni數(shù)據(jù)集的3個視角樣本數(shù)據(jù)中，視角1和視角2的3類樣本間都會出現(xiàn)一定的重疊現(xiàn)象，而視角3卻能夠清晰地顯示出3個類別的樣本，即視角3具備清晰的聚類特性。若使用現(xiàn)有的傳統(tǒng)單一視角聚類算法對此類聚類任務(wù)進行分析，得到的聚類結(jié)果將會受到視角1及視角2的影響，進而使得整體的聚類性能受到影響。對此，本文算法及相關(guān)算法均在該人工模擬數(shù)據(jù)集上進行了實驗，得到的實驗數(shù)據(jù)結(jié)果如表3及圖2所示。

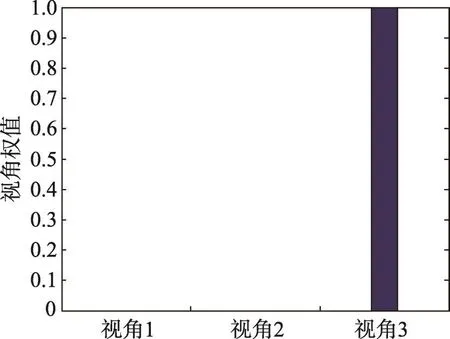
Fig.2 Weight of each view for IrisMoni datasets with W-CoMEC algorithm圖2　W-CoMEC算法獲取的IrisMoni數(shù)據(jù)集各視角權(quán)重

對表3的結(jié)果進行分析可以發(fā)現(xiàn)，與當前多任務(wù)的LSSMTC算法、組合任務(wù)的CombKM算法及基于樣本空間與特征空間協(xié)同分析的Co-clustering算法相比，多視角極大熵聚類算法CoMEC和W-CoMEC的聚類結(jié)果均明顯優(yōu)于它們的聚類性能；而與單一視角的極大熵聚類算法MEC相比，CoMEC和WCoMEC亦展現(xiàn)出穩(wěn)定的聚類性能。且由表3的評價指標也可以直觀地看到，W-CoMEC算法較CoMEC算法較之于多視角模糊聚類算法Co-FKM具有更好的聚類性能。此外，與多視角雙層變量自動加權(quán)聚類算法TWKM相比，CoMEC算法略顯不足，而其增強版本W(wǎng)-CoMEC算法的性能與之相當，這也體現(xiàn)了面向多視角數(shù)據(jù)的極大熵聚類方法具有處理多視角聚類任務(wù)的性能。

從圖2中展示出的增強版本W(wǎng)-CoMEC算法在IrisMoni數(shù)據(jù)集各視角權(quán)重分布情況也可以知道，該算法使得最佳視角權(quán)重達到最大，有效利用了最佳視角，進而獲取了更為合理的空間劃分結(jié)果。

綜上，各實驗指標的數(shù)據(jù)顯示，W-CoMEC算法利用視角加權(quán)的協(xié)同劃分的思想，使其可以有效處理多視角聚類任務(wù)，并表現(xiàn)出一定的聚類優(yōu)勢。

5.2多視角真實數(shù)據(jù)集實驗

本節(jié)選擇經(jīng)典機器學習數(shù)據(jù)庫UCI中的兩個具備多視角特性的數(shù)據(jù)集，即IS數(shù)據(jù)集和WTP數(shù)據(jù)集，針對這兩種真實多視角數(shù)據(jù)集來進一步進行性能評估。這兩種數(shù)據(jù)集的相關(guān)信息已在表1中給出，對這兩種多視角數(shù)據(jù)集的實驗結(jié)果如表4和表5。

由于LSSMTC算法本身的局限性，它需要在各視角樣本的維數(shù)相等的多視角數(shù)據(jù)中才能使用該算法，從而LSSMTC算法無法處理IS和WTP各視角維數(shù)均不相等的數(shù)據(jù)樣本。

Table 3 Experimental results of several algorithms on IrisMoni datasets表3　各算法在IrisMoni數(shù)據(jù)集上的實驗結(jié)果

此外，觀察表4和表5中的實驗結(jié)果可知，與LSSMTC、CombKM和Co-clustering算法相比，本文多視角極大熵聚類算法性能上有了進一步的改進。在比較的幾種算法中，MEC和CombKM算法僅實現(xiàn)了各視角數(shù)據(jù)的簡單融合，因而性能較差。雖然Coclustering聚類針對多視角數(shù)據(jù)已具有一定的各視角之間的協(xié)作學習能力，但協(xié)作學習的程度不夠充分。而本文CoMEC算法僅實現(xiàn)了各視角的協(xié)同劃分，因此與視角加權(quán)的W-CoMEC算法相比，聚類性能較差。而與多視角模糊聚類算法Co-FKM相比，在IS數(shù)據(jù)集上的實驗結(jié)果。顯示出該算法優(yōu)于本文多視角極大熵聚類算法，在WTP數(shù)據(jù)集上卻不及本文算法的性能；與K-means框架的多視角雙層變量自動加權(quán)聚類算法TWKM相比，在IS數(shù)據(jù)集和WTP數(shù)據(jù)集上的實驗結(jié)果均展現(xiàn)出本文算法的聚類性能優(yōu)勢。

綜上，較之于幾種相關(guān)的算法，本文算法針對多視角數(shù)據(jù)采用視角加權(quán)的協(xié)同劃分策略，最終得到具有全局最優(yōu)劃分的聚類性能，使得經(jīng)典的極大熵聚類算法具有處理多視角數(shù)據(jù)的性能。

Table 4 Experimental results of several algorithms on IS datasets表4　各算法在IS數(shù)據(jù)集上的實驗結(jié)果

Table 5 Experimental results of several algorithms on WTP datasets表5　各算法在WTP數(shù)據(jù)集上的實驗結(jié)果記錄

5.3運行時間比較

本節(jié)針對IS和WTP兩個真實數(shù)據(jù)集，將本文提出的新算法及其他對比算法在對應(yīng)數(shù)據(jù)集上的運行時間進行比較，具體如表6所示。由于LSSMTC算法要求各數(shù)據(jù)樣本維數(shù)相等無法使用，故未能記錄該算法的運行時間。表6中記錄均是算法在各個數(shù)據(jù)集上在給定參數(shù)時運行一次所用的時間，單位為秒。

由表6中的結(jié)果可以看出，在IS和WTP真實數(shù)據(jù)集上，本文提出的兩種新算法運行一次所用的時間都與MEC算法和CombKM算法差不多，與Coclustering算法相比，運行時間方面展現(xiàn)了較大的優(yōu)勢。同時，與Co-FKM和TWKM兩種多視角聚類算法相比，運行時間方面同樣也展現(xiàn)出了一定的優(yōu)勢。

6　結(jié)束語

Table 6 Running time of several algorithms on IS and WTP datasets表6　各種算法在IS和WTP數(shù)據(jù)集上運行時間　s

本文在經(jīng)典MEC算法框架上，通過引入?yún)f(xié)同劃分技術(shù)和視角加權(quán)技術(shù)，提出了多視角協(xié)同劃分極大熵聚類算法及其增強版本的視角加權(quán)協(xié)同劃分極大熵聚類算法。在協(xié)同劃分學習參數(shù)的作用下，使得各個視角之間協(xié)調(diào)作用更加靈活，同時視角權(quán)重凸顯出了最佳視角，進而使得極大熵聚類算法具有處理多視角聚類任務(wù)的性能，并體現(xiàn)出一定的聚類優(yōu)勢。而本文實驗部分中無論是模擬數(shù)據(jù)集還是UCI真實數(shù)據(jù)集得到的對比數(shù)據(jù)，均顯示出本文方法具有處理多視角數(shù)據(jù)的聚類性能，并且在模擬數(shù)據(jù)集和WTP真實數(shù)據(jù)集上體現(xiàn)出更好的聚類性能。但由于本文采用的MEC框架中歐式距離的使用，使得在面對高維多視角聚類問題時仍面臨一定的考驗，當前距離學習方法的研究也成為后人研究的熱點，針對歐式距離的局限性，距離學習在多視角聚類中的應(yīng)用將會成為今后研究的重點。特別地，近年來廣受關(guān)注的軟子空間聚類對于高維數(shù)據(jù)聚類展現(xiàn)出了有希望的性能，因而本文的多視覺學習策略和軟子空間聚類技術(shù)融合來開發(fā)新的算法亦將是非常有意義的工作。

References:

[1] Li R P, Mukaidono M.Amaximum-entropy approach to fuzzy clustering[C]//Proceedings of the 4th IEEE International Conference on Fuzzy Systems and the 2nd International Fuzzy Engineering Symposium, Yokohama, Japan, Mar 20-24, 1995. Piscataway, USA: IEEE, 1995: 2227-2232.

[2] Karayiannis N B. MECA: maximum entropy clustering algorithm[C]//Proceedings of the 3rd IEEE Conference on Computational Intelligence, Orlando, USA, Jun 26-29, 1994. Piscataway, USA: IEEE, 1994: 630-635.

[3] Zhang Zhihua, Zheng Nanning, Shi Gang. Maximum entropy clustering algorithm and its global convergence analysis[J]. Science: E Series, 2001, 31(1): 59-70.

[4] Deng Zhaohong, Wang Shitong, Wu Xisheng, et al. Robust maximum entropy clustering algorithm RMEC and its outlier labeling[J]. Engineering Science, 2004, 6(9): 38-45.

[5] Qian Pengjiang, Sun Shouwei, Jiang Yizhang, et al. Knowledge transfer based maximum entropy clustering[J]. Control and Decision, 2015, 30(6): 1000-1006.

[6] Asur S, Ucar D, Parthasarathy S. An ensemble framework for clustering protein-protein interaction networks[J]. Bioinformatics, 2007, 23(13): i29-i40.

[7] Wang Hongjun, Shan Hanhuai, Banerjee A. Bayesian cluster ensembles[J]. Statistical Analysis and Data Mining: The ASAData Science Journal, 2011, 4(1): 54-70.

[8] Yamanishi Y, Vert J P, Kanehisa M. Protein network inference from multiple genomic data: a supervised approach[J]. Bioinformatics, 2004, 20(S1): i363-i370.

[9] Virginia R de Sa. Spectral clustering with two views[C]// Proceedings of the 22nd International Conference on Machine Learning Workshop on Learning, Multiple Views, Bonn, Germany, Aug 7-11, 2005. New York, USA: ACM, 2005: 20-27.

[10] Zhou Dengyong, Burges C J C. Spectral clustering and transductive learning with multiple views[C]//Proceedings of the 24th International Conference on Machine Learning, Corvallis, USA, Jun 20-24, 2007. New York, USA: ACM, 2007: 1159-1166.

[11] Pedrycz W. Collaborative fuzzy clustering[J]. Pattern Recognition Letter, 2002, 23(14): 1675-1686.

[12] Cleuziou G, Exbrayat M, Martin L, et al. CoFKM: a centralized method for multiple-view clustering[C]//Proceedings of the 9th IEEE International Conference on Data Mining, Miami, USA, Dec 6-9, 2009. Piscataway, USA: IEEE, 2009: 752-757.

[13] Chen Xiaojun, Xu Xiaofei, Huang J Z, et al. TW-k-means: automated two-level variable weighting clustering algorithm for multiview data[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(4): 932-944.

[14] Gu Quanquan, Zhou Jie. Learning the shared subspace for multi-task clustering and transductive transfer classification [C]//Proceedings of the 19th IEEE International Conference on Data Mining, Miami, USA, Dec 6-9, 2009. Piscataway, USA: IEEE, 2009: 159-168.

[15] Gu Quanquan, Zhou Jie. Co-clustering on manifolds[C]// Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, Jun 28-Jul 1, 2009. New York, USA: ACM, 2009: 359-368.

[16] Zangwill W I. Convergence conditions for nonlinear programming algorithms[J]. Management Science, 1969, 16(1): 1-13.

[17] Luenberger D G, Ye Yinyu. Linear and nonlinear programming[M]. [S.l.]: Springer Science & Business Media, 2008.

[18] Bache K, Lichman M. UCI machine learning repository[EB/OL]. (2013)[2015-03-12]. http://archive.ics.uci.edu/ml.

[19] Liu Yi, Jin Rong, Jain A K. Boostcluster: boosting clustering by pairwise constraints[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, USA, Aug 12-15, 2007. New York, USA:ACM, 2007: 450-459.

[20] Jing Liping, Ng M K, Huang J Z. An entropy weighting kmeans algorithm for subspace clustering of high-dimensional sparse data[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(8): 1026-1041.

[21] Deng Zhaohong, Choi K S, Chung F L, et al. Enhanced softsubspace clustering integrating within-cluster and betweencluster information[J]. Pattern Recognition, 2010, 43(3): 767-781.

附中文參考文獻：

[3]張志華,鄭南寧,史罡.極大熵聚類算法及其全局收斂性分析[J].中國科學: E輯, 2001, 31(1): 59-70.

[4]鄧趙紅,王士同,吳錫生,等.魯棒的極大熵聚類算法RMEC及其例外點標識[J].中國工程科學, 2004, 6(9): 38-45.

[5]錢鵬江,孫壽偉,蔣亦樟,等.知識遷移極大熵聚類算法[J].控制與決策, 2015, 30(6): 1000-1006.

ZHANG Dandan was born in 1992. She is an M.S. candidate at School of Digital Media, Jiangnan University. Her research interests include artificial intelligence and intelligent computation.

張丹丹（1992—），女，江南大學數(shù)字媒體學院碩士研究生，主要研究領(lǐng)域為人工智能，智能計算。

DENG Zhaohong was born in 1982. He is an associate professor at School of Digital Media, Jiangnan University. His research interests include fuzzy modeling and intelligent computation.

鄧趙紅（1982—），男，博士，江南大學數(shù)字媒體學院副教授，主要研究領(lǐng)域為模糊建模，智能計算。

WANG Shitong was born in 1964. He is a professor at School of Digital Media, Jiangnan University. His research interests include artificial intelligence, pattern recognition and bioinformatics.

王士同（1964—），男，江南大學數(shù)字媒體學院教授，主要研究領(lǐng)域為人工智能，模式識別，生物信息。

Maximum Entropy Clustering Algorithm for Multi-View Data?

ZHANG Dandan+, DENG Zhaohong, WANG Shitong
School of Digital Media, Jiangnan University, Wuxi, Jiangsu 214122, China

+ Corresponding author: E-mail: zdd1226394625@163.com

ZHANG Dandan, DENG Zhaohong, WANG Shitong. Maximum entropy clustering algorithm for multi-view data. Journal of Frontiers of Computer Science and Technology, 2016, 10(4): 554-564.

Abstract:Currently, the maximum entropy clustering (MEC) merges the multi-view samples to process the multi-view clustering task. However, this will damage the independence of each view, and affect the final partition results. Aiming at this problem, this paper proposes a multi- view collaborative partition maximum entropy clustering (CoMEC) algorithm, which joins a constraint to coordinate each perspective space partition, to make each view in a separate clustering process consider the influence of other views. Then this paper proposes the enhanced weighted view version called W-CoMEC by identifying the importance of each view. Finally this paper applies the geometric average integration strategy to obtain the global partition results. The experimental results on a synthetic multi-view dataset and several UCI real-world multi-view datasets show that the proposed algorithm outperforms or is at least comparable to the existing clustering technology in dealing with multi-view clustering task.

Key words:entropy; multi-view clustering; partition; weight; integration strategy; UCI dataset

文獻標志碼：A

中圖分類號：TP18

doi:10.3778/j.issn.1673-9418.1505041