分數階PDμ控制器與常規PD控制器在倒立擺中的應用研究
賈瑞強


摘 要:對比分析分數階PDμ控制器與常規PD控制器在倒立擺系統中的控制性能。以直線一級倒立擺為被控對象,利用牛頓-歐拉方法創建了整個系統的狀態空間方程。提出了雙回路PD控制方案,對倒立擺的兩個被控變量一同進行閉環控制,分別設計了常規PD控制器和分數階PDμ控制器,并在Matlab中對系統實施了仿真。由仿真結果可知,兩種控制策略均能完成倒立擺的穩定控制,但分數階PDμ控制器使整個系統有較小的超調量,震蕩小,調節時間短,較常規PD控制器有更好的控制效果。
關鍵詞:直線一級倒立擺;分數階PDμ控制器;常規PD控制器;MATLAB
0 引言
直線一級倒立擺是一個不穩定、多變量的非線性系統,對其施加的控制需要微型計算機、控制工程、傳感器等多個領域的相關知識。倒立擺廣泛應用在實際的控制實驗測試中,它能夠進行系統魯棒性、穩定性和可控制性等特性的分析。倒立擺的原理已經不再停留在實驗研究的初步階段,目前它被運用在各種工程中。因此,對倒立擺的探究既具有很強的理論價值,又有很強的實際價值。
整篇文章主要以倒立擺為具體的研究目標,憑借常規PID控制策略與分數階PID控制策略的理論基礎,使用Matlab仿真,完成倒立擺模型創建、控制器設計與仿真研究,最后對比分析了兩種PID控制方法。
1 系統建模
倒立擺自身固然是不穩定的系統,當忽視掉空氣阻力和種種摩擦等成分后,便是經典的運動的剛體系統[1-2]。可以應用經典力學理論的相關知識體系在慣性坐標系內創建系統的動力學方程。因此整個倒立擺的精確數學模型可以用牛頓—歐拉方法來創建。
2 常規PD控制器設計
PID控制器是應用最為廣泛、技術最成熟的控制器[3]。雖然種種新型控制器不斷出現,但PID控制器仍舊以其結構簡單、魯棒性強等長處,占有主導地位。PID控制器由比例單元P、積分單元I和微分單元D組成,經由Kp,Ki和Kd 3個參數的調節來達到良好的控制效果。其傳遞函數為:
由數學模型可以知道,單級倒立擺是一個單輸入雙輸出的被控對象,為此本文提出雙回路PD控制方案,這樣可對系統的兩個被控變量同時進行閉環調節,完成倒立擺的穩定控制。其模型與狀態反饋控制系統的模型相同,所以可通過極點配置法得到PD控制器的六個參數。取期望極點為μ1=-10,μ2=-10,μ3=-1.432+j1.671,μ4=-1.432-j1.671,在Matlab中求取反饋增益矩陣為:
[-10.0266 -7.9349 44.9897 6.2855] (2)
3 分數階PDμ控制器設計
常規PID控制器的3個系統變量Kp,Ki,Kd一樣是分數階PIλDμ控制器可整定的變量,同時它又多了兩個可調變量λ與μ。由于λ與μ值可以取值為分數,而不只是常規PID控制器中的1或另外的整數,故分數階PIλDμ控制器變量的可調節區域更加廣泛,能夠更靈活地調節被控系統,以便獲得更好的控制結果。
分數階PIλDμ控制器傳遞函數為
同上,這里也采用雙回路分數階PDμ控制策略,同樣取以上期望極點,采用微粒群優化算法[4]得到控制器參數=-15.5326,= -22.6401,= 137.5812,=25.9820,α= 0.8952,β= 1,0384。
4 仿真結果分析
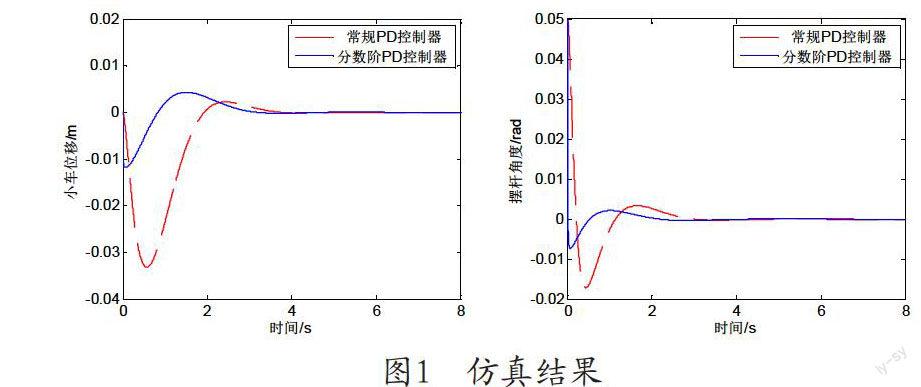
設小車位移x的初始值為0,擺桿角度的初始值為0.05rad。仿真結果如圖1,可得出,兩種控制策略均能使小車位移靜止在零位,保持穩定狀態,但分數階PDμ控制器使小車位移有較小的超調量,系統震蕩小,調節時間短。兩種控制策略也可使擺桿角度靜止在零位,保持倒立穩定狀態,但分數階PDμ控制器使擺桿角度有較小的超調量,震蕩小,響應速度快。
5 結論
文中以倒立擺為被控對象,利用牛頓-歐拉方法創建了整個系統的狀態空間方程。提出了雙回路PD控制方案,對倒立擺的兩個被控變量一同進行閉環控制,分別設計了常規PD控制器和分數階PDμ控制器,并在Matlab中對系統實施了仿真。由仿真結果可以知道,兩種控制策略均能完成倒立擺的穩定控制,但分數階PDμ控制器使整個系統有較小的超調量,震蕩小,調節時間短,較常規PD控制器有更好的控制效果。
參考文獻
[1]劉惠超,孔慶忠.最優控制方法在直線倒立擺中的應用[J].機械制造與自動化,2015,(5):189-191.
[2]張白莉.單級倒立擺控制系統的穩定性算法設計[J].現代電子技術,2011,(3):120-122.
[3]梁春輝,馮雷,張欣.直線一級倒立擺控制策略研究及仿真分析[J].長春工程學院學報(自然科學版),2010,(1):36-40.
[4]李明杰,趙志誠,桑海.單級倒立擺的分數階PI-λD-μ控制器設計[J].太原科技大學學報,2014,(1):19-23.
(作者單位:石家莊鐵道大學機械工程學院)

