一種改進的投影孿生支持向量機
花小朋,孫一顆,丁世飛
(1.鹽城工學院 信息工程學院,江蘇 鹽城 224051; 2. 中國礦業大學 計算機學院,江蘇 徐州 221116)
?
一種改進的投影孿生支持向量機
花小朋1,孫一顆1,丁世飛2
(1.鹽城工學院 信息工程學院,江蘇 鹽城 224051; 2. 中國礦業大學 計算機學院,江蘇 徐州 221116)
摘要:針對投影孿生支持向量機(PTSVM)在訓練階段欠考慮樣本空間局部結構和局部信息的缺陷,提出一種具有一定局部學習能力的有監督分類方法:加權投影孿生支持向量機(weighted PTSVM,WPTSVM)。相比于PTSVM,WPTSVM優勢在于:通過構造類內近鄰圖為每個樣本獲取特定的權值,并且以加權均值取代標準均值,在一定程度上提高了算法的局部學習能力;選取異類樣本集中少量邊界點構造優化問題的約束條件,很大程度上降低了二次規劃求解的時間復雜度;繼承了PTSVM的優點,可以看成PTSVM的推廣算法。理論分析及其在人造數據集和真實數據集上的測試結果表明該方法具有上述優勢。
關鍵詞:分類;投影孿生支持向量機;局部信息;加權均值;近鄰圖;二次規劃;約束條件;時間復雜度
在分類問題中,經典支持向量機(SVM)依據間隔最大化準則生成分類決策面,存在訓練時間復雜度偏高和欠考慮樣本分布情況的缺陷[1-2]。近年來,作為經典SVM的改進方法,非平行超平面分類器(nonparellel hyperplane classifiers,NHCs)[3]已經成為模式識別領域新的研究熱點之一。孿生支持向量機(twin support vector machine,TWSVM)[4]是NHCs方法中主要代表性算法之一,其主要思想源于泛化特征值中心支持向量機(generalized eigenvalue proximal SVM,GEPSVM)[5]。TWSVM將GEPSVM中兩個優化子問題轉換成兩個形如SVM的小規模二次規劃問題,從而使其訓練時間復雜度縮減為經典SVM的1/4。除了訓練速度上的優勢,TWSVM還繼承了GEPSVM能夠在線性模式很好地處理異或(XOR)樣本分類問題的優勢。然而,當兩類樣本具有不同散度分布時,TWSVM的泛化性能欠佳[6]。文獻[7]提出一種新的非平行超平面分類器:投影孿生支持向量機 (projection twin support vector machine,PTSVM)。與TWSVM不同的是,PTSVM優化目的是為每類樣本尋找最佳投影軸,而且通過遞歸迭代算法,PTSVM能夠生成多個正交投影軸。實驗結果表明,PTSVM對復雜的XOR問題具有更好的分類能力。為解決非線性分類問題。文獻[8]進一步提出PTSVM的非線性方法。
然而分析發現,PTSVM在訓練過程中僅僅考慮樣本空間的全局結構和全局信息,忽視了樣本空間的局部結構和局部信息。許多研究結果表明同類數據集中大部分樣本在局部上是關聯的(即數據集中存在潛藏的局部幾何結構),而這種內在的局部信息對數據分類又是至關重要的[9]。這種潛在的局部信息可以通過數據集中樣本間的k近鄰關系進行挖掘[9-11]。
基于上述分析,本文基于PTSVM提出一種新的具有一定局部學習能力的非平行超平面分類器算法:加權投影孿生支持向量機(weighted PTSVM,WPTSVM)。相比于PTSVM,WPTSVM優勢體現在以下4個方面:1)通過構造類內近鄰圖為每個樣本獲取特定的權值,并且以加權均值取代標準均值,在一定程度上提高了算法的局部學習能力;2)選取異類樣本集中少量邊界點構造優化問題的約束條件,很大程度上降低了二次規劃求解的時間復雜度;3)WPTSVM繼承了PTSVM的優點,可以看成PTSVM的推廣算法。4)WPTSVM具有更好分類性能。
1投影孿生支持向量機(PTSVM)

第1類超平面的優化準則
(2)
式中C1是懲罰參數,l為損失變量。
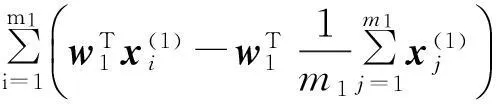
2加權投影孿生支持向量機(WPTSVM)
2.1算法構造
為刻畫同類樣本集內在的緊湊型和異類樣本集間的分散性,依據圖論[10,12]為每類決策面構建類內近鄰圖Gs和類間近鄰圖Gd。
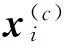
(3)
式中:t為熱核參數,Ne(x)表示x的k近鄰樣本集。
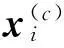
(4)
(5)
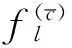
定義 3WPTSVM算法中,第1類訓練樣本集相應決策超平面的優化準則WPTSVM-1:
(6)
第2類超平面優化準則WPTSVM-2:
(7)
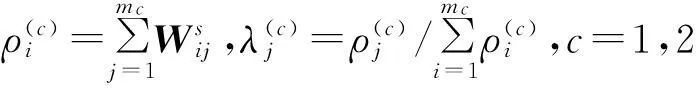
(8)
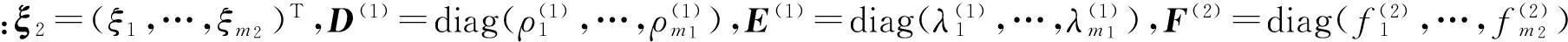
類似于傳統SVM求解方法,通過引入拉格朗日函數生成式(8)的對偶問題
(9)
式中α=[α1,α2,…,αm2]T。
由此對偶問題的求解可得原問題式(6)中投影軸w1。類似的方法,可求原問題式(7)中投影軸w2。
對于未知樣本x,WPTSVM的決策函數為
(10)
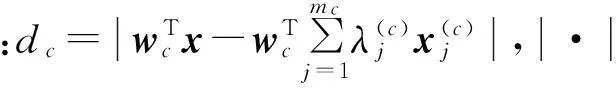
2.2算法分析
這里以WPTSVM的第1類樣本優化問題WPTSVM-1為例進行算法分析,第2類樣本優化問題WPTSVM-2有類似的算法分析。
定理1式(9)為凸二次規劃。
證明式(9)核矩陣:
定理 2假定α是對偶問題式(9)的解,則w1是原優化問題式(6)的全局最優解。
證明由定理1的證明可得,式(9)為凸二次規劃問題,又依據文獻[14]中引理3的滿足條件可知,該二次規劃的解為全局最優解。證畢。
2.3算法比較
2.3.1泛化性能
定理 3PTSVM是WPTSVM的特例。
證明考慮WPTSVM的第1類樣本的優化準則(7)。令D(1)=I∈Rm1×m1,F(2)=I∈Rm2×m2,則式(7)轉化為PTSVM的第1類樣本的優化準則(2)。對于WPTSVM的第2類樣本的優化準則(8)有類似的特性。因此,PTSVM是WPTSVM的特例,而WPTSVM是PTSVM的推廣算法。證畢。
定理3說明了本文提出的WPTSVM算法繼承了PTSVM的優點。進一步比較式(7)和(2)可知, PTSVM僅僅考慮類內樣本的全局信息,而WPTSVM用加權均值代替PTSVM中標準均值,可以在一定程度上提高算法的局部學習能力,因為基于近鄰圖的加權均值比起標準均值更能體現樣本空間的局部結構[13]。除此之外,WPTSVM還在優化目標函數中引入了樣本權值,權值越大,說明該樣本越重要,對保持訓練樣本集潛在局部信息的貢獻程度越大。圖1給出了WPTSVM與PTSVM在人造數據集上的分類決策面。不難看出,WPTSVM的決策面能夠在一定程度上體現樣本集內在局部流形結構,而PTSVM相對較弱。
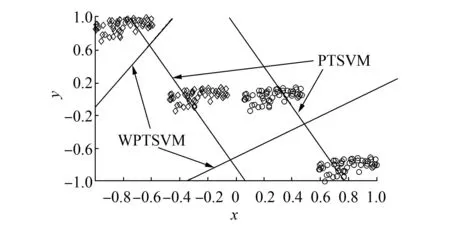
圖1 兩種算法人造數據集上的比較Fig.1 Comparision of two algorithms on artificial dataset
2.3.2訓練時間復雜度
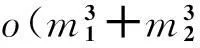
2.3.3構造非線性分類算法
針對線性不可分情況,本文進一步提出基于核空間的非線性WPTSVM算法——NWPTSVM。
定義4NWPTSVM的第1類超平面的優化準則為
(11)
第2類超平面的優化準則為
(12)
通過引入拉格朗日函數,可按照類似上述WPTSVM算法的推導過程分別得出式(11)和(12)的對偶形式,然后通過二次規劃求解可求得投影矢量u1和u2。NWPTSVM的決策函數為
(13)
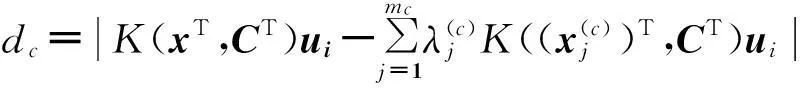
3實驗分析
實驗選用人造數據集和真實數據集,進一步驗證本文WPTSVM方法的有效性。實驗環境:2.3 GHz CPU,2 GB內存,實驗軟件MATLAB 7.1。
3.1復雜交叉數據集
相對于經典SVM,線性模式下對XOR問題的測試能力是非平行超平面分離器優勢之一[3-5]。因此,本節首先驗證MPTSVM測試交叉數據集的能力。圖2給出一種較復雜的人造交叉數據集:Comxor[7]。表1給出了TWSVM、PTSVM和WPTSVM三種算法在該測試數據集上10折交叉驗證結果。參數C1與C2的搜索范圍為{2i|i=-8,-6,…,+8};WPTSVM中類內近鄰參數k1的搜索范圍為{1,2,…,9},類間近鄰參數k2=5,熱核參數t的搜索范圍為{2i|i=-1,0,…,8}。從表1實驗結果來看,PTSVM分類性能優于TWSVM,而本文WPTSVM則具有更佳的分類性能。

圖2 復雜交叉數據集Fig.2 Compxor dataset
Table 1Classification comparision of three algorithms on comxor dataset

DatasetTWSVMPTSVMWPTSVMComxor93.76±6.7095.67±4.7397.36±2.90
3.2流形數據集
數據集two-moons (如圖3所示) 的結構具有明顯局部流形,所以該數據集多用于測試算法的局部學習能力[2,13]。這里通過測試two-moons數據集,并與TWSVM和PTSVM方法進行比較,驗證本文WPTSVM方法局部學習能力。
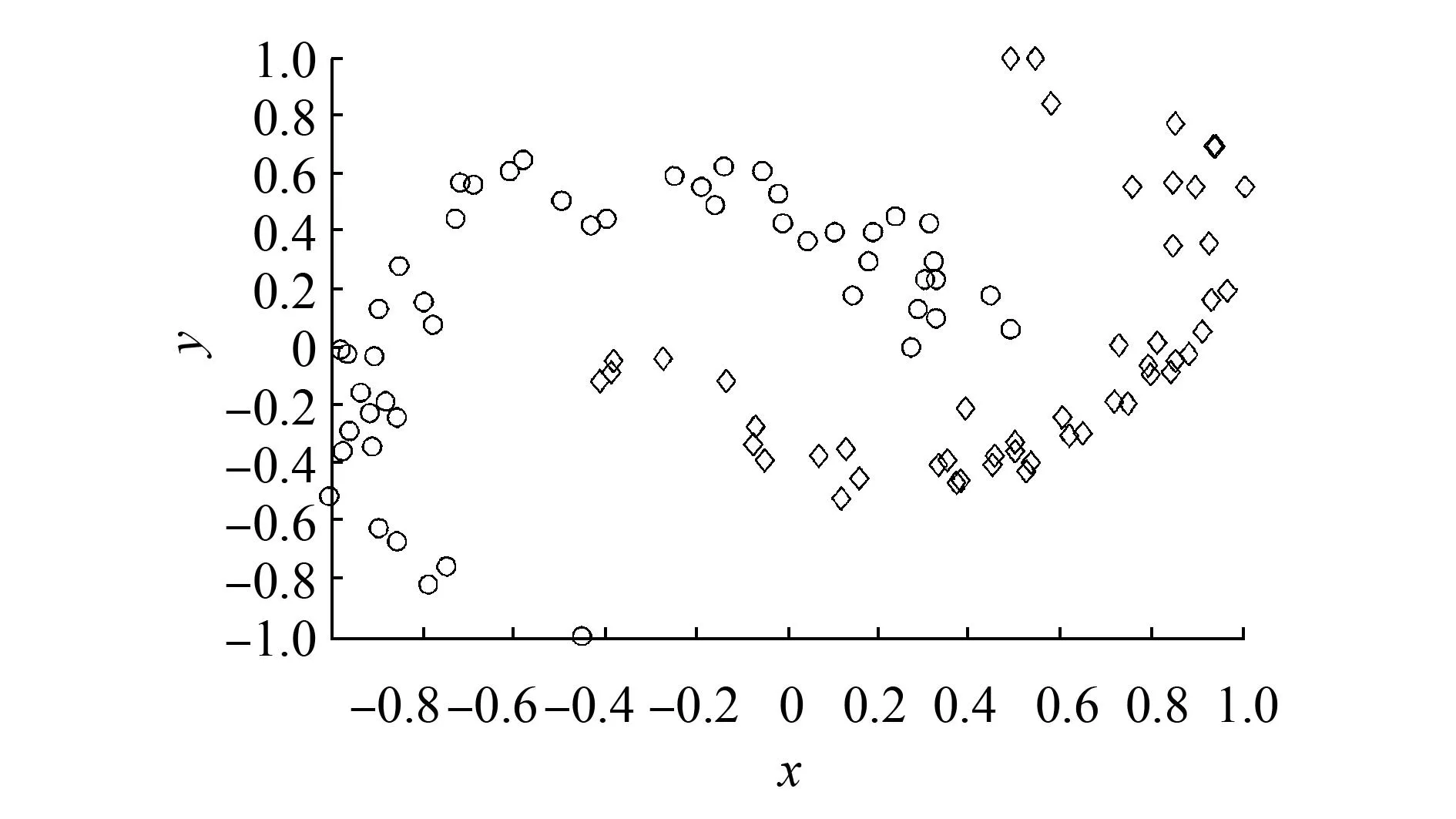
圖3 Two-moons數據集Fig.3 Two-moons dataset
實驗選擇正負類樣本各為50的two-moons數據集。隨機抽取40%訓練集和60%測試集進行實驗,重復此過程10次并記錄實驗結果的平均值
(見表2)。顯然,WPTSVM方法具有更好的測試效果,這說明本文加權措施的確能夠在一定程度上提高PTSVM算法的局部學習能力。
表23種算法在雙月形數據集上的分類精度(%)比較
Table 2Classification comparision of three algorithms on two-moons dataset

DatasetTWSVMPTSVMWPTSVMtwo-moons77.17±13.7276.33±12.3678.83±8.86
3.3UCI數據集
UCI數據集經常被用來驗證算法的分類精度[3-7,15-16]。該數據集包含若干數據子集,涉及諸多應用領域。
實驗中選取部分數據子集,利用10-折交叉驗證法測試算法分類性能。非線性算法實驗中,選擇高斯核exp(-‖xi-xj‖2/σ)作為核函數,參數σ的搜索范圍為{2i|i=-1,0, …,7},其他參數搜索范圍同3.1節。線性模式及非線性模式下實驗結果如表3和表4分別所示。
從訓練時間上看: TWSVM與PTSVM相當,WPTSVM明顯比這兩種算法快。原因是WPTSVM選用少量邊界樣本進行二次規劃求解,而其他兩種算法則選擇異類中全部樣本。
從分類性能上看:本文提出的WPTSVM 算法具有更好的分類能力,這也進一步佐證了本文提高PTSVM算法局部學習能力的措施確實有效。
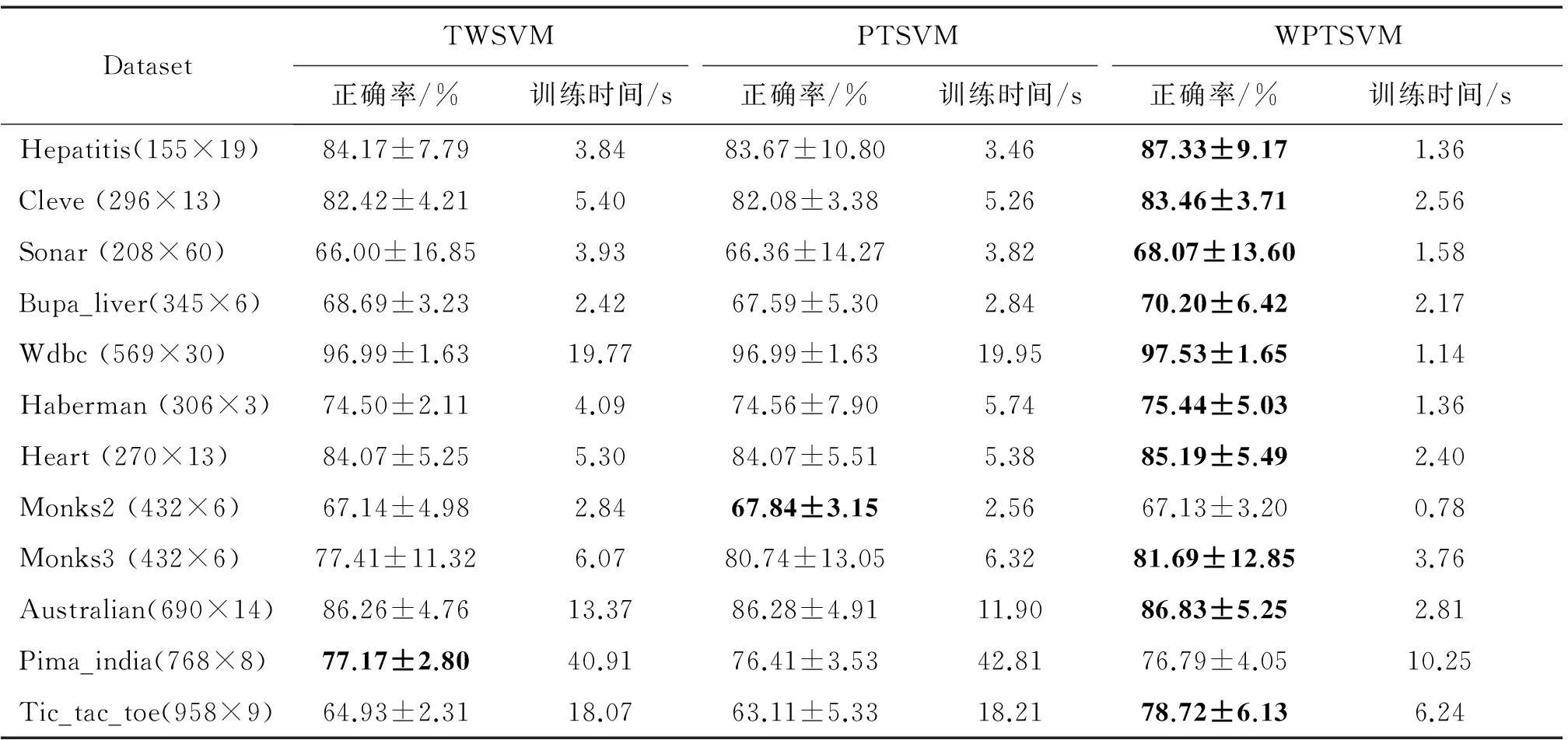
表3 線性模式下3種算法的實驗比較
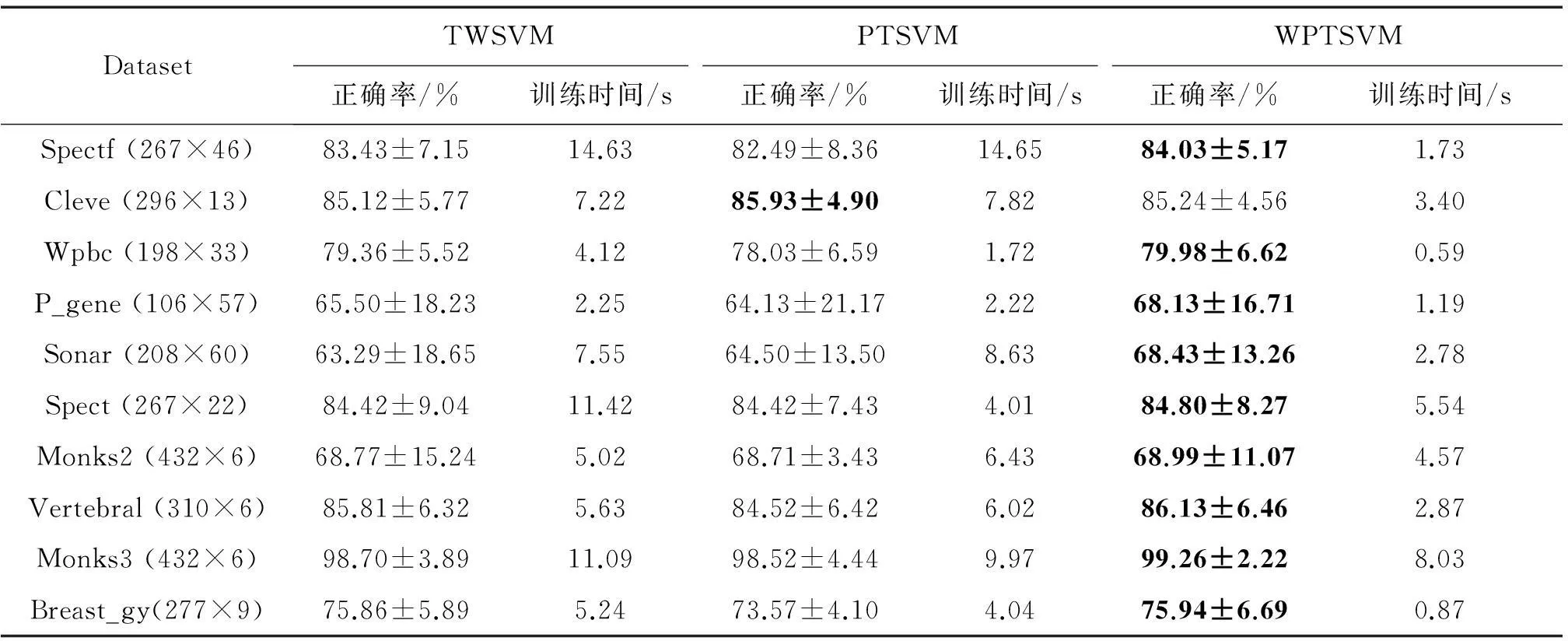
表4 非線性模式下3種算法的實驗比較
4結束語
本文基于投影孿生支持向量機(PTSVM )提出一種新的的非平行超平面分類器方法:加權投影孿生支持向量機(WPTSVM )。WPTSVM不僅繼承了PTSVM方法的優點,而且在一定程度上提高了算法局部學習能力。除此之外,WPTSVM通過類間近鄰圖選擇少量邊界樣本構造優化問題約束條件,相當程度上降低了二次規劃求解時間復雜度。理論分析及實驗結果均驗證了本文所提算法的有效性。誠然,WPTSVM在構造類內及類間近鄰圖時,需要花費額外的計算開銷,特別是在學習樣本數目較大時,算法計算復雜度會偏高,這也是今后進一步研究的目標。
參考文獻:
[1]皋軍, 王士同, 鄧趙紅. 基于全局和局部保持的半監督支持向量機[J]. 電子學報, 2010, 38(7): 1626-1633.
GAO Jun, WANG Shitong, DENG Zhaohong. Global and local preserving based semi-supervised support vector machine[J]. Acta electronica sinica, 2010, 38(7): 1626-1633.
[2]花小朋, 丁世飛. 局部保持對支持向量機[J]. 計算機研究與發展, 2014, 51(3): 590-597.
HUAxiaopeng, DING Shifei. Locality preserving twin support vector machines [J]. Journal of computer research and development, 2014, 51(3): 590-597.
[3] DING Shifei, HUA Xiaopeng, YU Junzhao. An overview on nonparallel hyperplane support vector machines[J]. Neural computing and applications, 2014, 25(5): 975-982.
[4]JAYADEVA, KHEMCHAND R, CHANDRA S. Twin support vector machines for pattern classification [J]. IEEE transaction on pattern analysis and machine intelligence, 2007, 29 (5): 905-910.
[5]MANGASARIAN O L, WILD E W. MultisurFace proximal support vector machine classification via generalized eigenvalues [J]. IEEE transactions on pattern analysis and machine intelligence, 2006, 28 (1): 69-74.
[6] PENG Xinjun,XU Dong. Bi-density twin support vector machines for pattern recognition[J]. Neurocomputing, 2013, 99: 134-143.
[7] CHEN Xiaobo, YANG Jian, YE Qiaolin, et al. Recursive projection twin support vector machine via within-class variance minimization[J]. Pattern recognition, 2011, 44 (10/11): 2643-2655.
[8]SHAO Yuanhai, WANG Zhen, CHEN Weijie, et al. A regularization for the projection twin support vector machine[J]. Knowledge-based systems, 2013, 37 (1): 203-210.
[9]YANG Xubing, CHEN Songcan, CHEN Bin, et al. Proximal support vector machine using local information [J]. Neurocomputing, 2009, 73(1): 357-365.
[10]COVER T M, HART P E. Nearest neighbor pattern classification[J]. IEEE transactions on information theory, 1967, 13 (1): 21-27.
[11]WANG Xiaoming, CHUNG Fulai, WANG Shitong. On minimum class locality preserving variance support vector machine[J]. Patter recognition, 2010, 43(8): 2753-2762.
[12]YE Qiaolin, ZhAO Chunxia, YE Ning, et al. Localized twin svm via convex minimization[J]. Neurocomputing, 2011, 74(4): 580-587.
[13]皋軍, 黃麗莉, 王士同. 基于局部子域的最大間距判別分析 [J ]. 控制與決策, 2014, 29 (5): 827-832.
GAO Jun, HUANG Lili, WANG Shitong. Local sub-domains based maximum margin criterion [J]. Control and decision, 2014, 29 (5): 827-832.
[14]鄧乃楊, 田英杰. 支持向量機—理論、算法與拓展[M]. 北京: 科學出版社, 2009: 164-223.
[15]丁立中, 廖士中. KMA-a: 一個支持向量機核矩陣的近似計算算法[J]. 計算機研究與發展, 2012, 49(4): 746-753.
DING Lizhong, LIAO Shizhong. KMA-a: a kernel matrix approximation algorithm for support vector machines [J]. Journal of computer research and development, 2012, 49(4): 746-753.
[16]XUE Hui, CHEN Songchan. Glocalization pursuit support vector machine [J].Neural computing and applications, 2011, 20(7):1043-1053.

花小朋,男,1975年生,副教授,博士,主要研究方向為機器學習與數據挖掘,發表學術論文10余篇。

孫一顆,男,1993年生,碩士研究生,主要研究方向為機器學習、數據挖掘,申請發明專利2項。

丁世飛,男,1963年生,教授,博士生導師,中國計算機學會高級會員,中國人工智能學會高級會員,江蘇省計算機學會人工智能專業委員會委員,主要研究方向為智能信息處理,目前主持國家973項目1項、國家自然科學基金項目1項,發表學術論文60余篇。
中文引用格式:花小朋,孫一顆,丁世飛.一種改進的投影孿生支持向量機[J]. 智能系統學報, 2016, 11(3): 384-391.
英文引用格式:HUA Xiaopeng, SUN Yike, DING Shifei. An improved projection twin support vector machine[J]. CAAI transactions on intelligent systems, 2016, 11(3): 384-391.
An improved projection twin support vector machine
HUA Xiaopeng1, SUN Yike1, DING Shifei2
(1. School of Information Engineering, Yancheng Institute of Technology, Yancheng 224051, China; 2. School of Computer Science and Technology, China University of Mining and Technology, Xuzhou 221116, China)
Abstract:A supervised classification method having a local learning ability, called weighted projection twin support vector machine (WPTSVM), is proposed. This method aims to improve upon a defect that projection twin support vector machines (PTSVMs) have, namely, that PTSVMs do not take account of the local structure and local information of a sample space in the training process. Compared with PTSVM, WPTSVM improves its local learning ability to some extent by attaching different weights for each sample according to the within-class neighborhood graph and replacing the standard mean with a weighted mean. Moreover, to reduce computational complexity, WPTSVM chooses a small number of boundary points in the contrary-class based on the between-class neighborhood graph to construct constraints of the original optimization problems. The method inherits the merits of PTSVM and can be regarded as an improved version of PTSVM. Experimental results on artificial and real datasets indicate the effectiveness of the WPTSVM method.
Keywords:classification; projection twin support vector machine; local information; weighted mean; neighborhood graph; quadratic programming; constraint condition; time complexity
作者簡介:
中圖分類號:TP391.4
文獻標志碼:A
文章編號:1673-4785(2016)03-0384-06
通信作者:花小朋. E-mail:xp_hua@163.com.
基金項目:國家重點基礎研究計劃項目(2013CB329502);國家自然科學基金項目(61379101); 江蘇省自然科學基金項目(BK20151299).
收稿日期:2016-03-20.網絡出版日期:2016-05-13.
DOI:10.11992/tis.2016030.
網絡出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20160513.0924.024.html

