基于GA-GRNN的露天礦山邊坡穩定性評價*

陳　梵　章　光　王丹丹　李墨瀟

(武漢理工大學資源與環境工程學院)

?

基于GA-GRNN的露天礦山邊坡穩定性評價*

陳梵章光王丹丹李墨瀟

(武漢理工大學資源與環境工程學院)

摘要邊坡失穩是露天礦山常見的地質災害，快速確定邊坡的穩定狀態對于確保礦山安全生產意義重大。利用廣義回歸神經網絡(General regression network, GRNN)的非線性逼近性能并結合遺傳算法(Genetic algorithm,GA)的非線性尋優性能對某露天礦山的邊坡安全系數進行了預測，結果表明：基于遺傳算法優化的廣義回歸神經網絡(GA-GRNN)對露天礦山邊坡安全系數的預測結果較為精確，且預測速度較快，為實際工程中快速判斷露天礦山邊坡的穩定狀態提供參考。

關鍵詞露天礦山邊坡穩定性安全系數遺傳算法廣義回歸神經網絡

目前，邊坡穩定性分析方法主要有極限平衡法、工程地質分析法、數值模擬法、可靠性分析法等，該類方法雖然考慮了邊坡的主要因素，但由于計算繁瑣，較難準確描述非線性特征，且未能有效顧及邊坡穩定性影響因素的模糊性、隨機性、不確定性等特點，因而無法實現對邊坡穩定性進行快速預測[1-3]。人工神經網絡(Artificial neural network,ANN)與各類算法的結合可實現對邊坡穩定性的快速、準確預測，在一定程度上彌補了傳統方法的不足[4-8]。廣義回歸神經網絡(GRNN)的非線性逼近性能及容錯率均較優，可適用于小樣本問題，且其結構固定，可更快的進行訓練，但該算法通過人為調節參數光滑因子(σ)，對預測精度影響較大[9]。為此，采用遺傳算法優化的廣義回歸神經網絡(GA-GRNN)對某露天礦山邊坡安全系數進行預測，有助于降低人為因素的影響，提高預測精度。

1算法原理

1.1廣義回歸神經網絡

1.2基于遺傳算法優化廣義回歸神經網絡

1.2.1遺傳算法原理

遺傳算法(GA)是一種有效的全局尋優算法，每次通過迭代借助交叉、突變產生新個體，逐漸擴大搜索范圍，可高效尋求全局最優解。該算法的基本要素為染色體編碼方法、適應度函數、遺傳操作和運行參數。用遺傳算法對GRNN建立的數學模型進行優化，在求解所優化的問題時不要求可微和連續，也無需了解函數的具體形式，即可實現離散變量的全局尋優。

1.2.2GA-GRNN預測步驟

GRNN的光滑因子(σ)需人為調節，且各神經元的σ都設置為同一個值，網絡的訓練過程即為對σ的單值尋優過程，并未考慮不同σ取值對輸出結果精度的影響，在一定程度上降低了網絡的預測精度。通過遺傳算法對GRNN進行優化，將每個σ值作為一個獨立變量，根據不同的神經元對輸出結果的不同影響程度，選取每個神經元對應的最優光滑因子，可消除采用單個光滑因子對網絡預測精度的影響。通過遺傳算法中的選擇、交叉、變異等操作篩選個體，淘汰適應度低的個體，適應度高的個體則被保留，產生新一代群體，通過反復循環上述流程，直至滿足條件為止。因而，采用遺傳算法搜索最優σ值，建立了GA-GRNN模型，具體步驟：①確定遺傳算法參數；②遺傳算法初始化，生成種群規模為NIND的GRNN光滑因子初始種群，進化代數g=0;③讀入學習樣本進行網絡訓練，按給定的適應度函數進行適應度評價；④采用遺傳算法按各個體的適應度大小進行選擇、交叉和變異操作，得到新的種群P(g+1)，進化代數g=g+1；⑤判斷是否達到最大進化代數，若已達到，則停止計算，返回適應度最高的個體；否則轉至③，直至達到最大進化代數；⑥輸出適應度最高的個體對應的實值數，即為最優的σ值；⑦用最優的σ值建立GA-GRNN模型，對測試樣本進行預測。

2應用實例

在構建GA-GRNN模型前，有必要選擇與邊坡失穩密切相關的因素(容重、黏聚力、內摩擦角、邊坡角、邊坡高度、孔隙水壓力比)作為輸入變量。將上述6個因素作為GRNN的輸入單元，輸出單元為邊坡的安全系數f。遺傳算法的種群規模為50，交叉概率0.6，變異概率0.1，迭代次數100。以某露天礦山邊坡數據為學習樣本和測試樣本，見表1[4-5]。

以表1中前32組數據為學習樣本，后5組數據為測試樣本。采用基于遺傳算法優化的BP神經網絡(GA-BP)、人為選取σ值(σ取0.3)的GRNN以及GA-GRNN進行邊坡危險性預測試驗，結果見表2。GA-GRNN的適應度曲線見圖1。為準確評價各模型性能，采用均方誤差(Mean square error,MSE)、平均誤差百分率(Mean percentage error，MAPE)評價模型精度，采用威爾莫特一致性指數評價模型的泛化性(Willmott's index of agreement，WIA)。

表1　樣本數據

表2　安全系數預測誤差

由表2、圖1可知：當種群進化至100代時，平均適應度極劇下降，GA-GRNN的適應度達到了最佳值。GA-GRNN的平均絕對誤差(2.57%)及最大相對誤差(小于4%)均優于GA-BP及GRNN。經計算得：MSE=0.29，MAPE=2.20，WIA=0.98，表明GA-GRNN模型具有較強的泛化能力，對新樣本具有很好的適應能力。

3結論

(1)在考慮邊坡穩定性多種影響因素的情況下，GA-GRNN可實現對露天礦山邊坡安全系數的高精度預測，預測結果與實際值的最大誤差小于4%，可滿足現場工程需要。

(2)GA-GRNN預測的準確性和穩定性優于GA-BP，且GA-GRNN的預測運算時間遠遠小于GA-BP，可實現對露天礦山邊坡安全系數的快速預測。

(3)GA-GRNN在預測過程中，無人為調節因素，輸出數據唯一，無需進行多次比較，實用性較強。

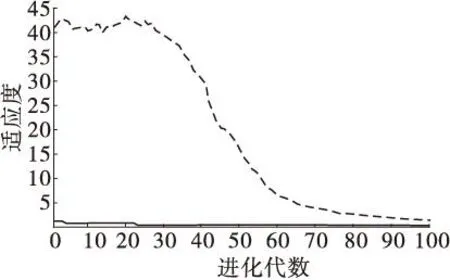
圖1　GA-GRNN適應度曲線

參考文獻

[1]倪凱軍，安海堂，張衛強.降雨入滲對邊坡穩定性影響的試驗研究[J].現代礦業，2015(11)：176-179.

[2]宋亮華，劉濤.基于重整化群語模糊可靠度法的邊坡穩定性分析[J].現代礦業，2015(6)：163-164.

[3]楊天鴻，張鋒春，于慶磊，等.露天礦高陡邊坡穩定性研究現狀及發展趨勢[J].巖土力學，2011，32(5)：1437-1451.

[4]劉先珊，周創兵.改進的邊坡巖體穩定性預測模型研究[J].巖石力學與工程學報，2005，24(19)：3492-3498.

[5]賀可強，雷建和.邊坡穩定性的神經網絡預測研究[J].地質與勘探，2001，37(6)：72-75.

[6]胡衛東，曹文貴.基于粒子群BP網絡混合算法的邊坡穩定性評價[J].鐵道科學與工程學報，2015(1)：66-71.

[7]劉思思.基于神經網絡及遺傳算法技術的邊坡穩定性評價研究[D].長沙：中南林業科技大學，2006.

[8]陳明.MATLAB神經網絡原理與實例精解[M].北京：清華大學出版社，2013.

[9]習施彥，韓力群，廉小親.神經網絡設計方法與實例分析[M].北京：北京郵電大學出版社，2009.

(收稿日期2015-06-25)

*高等學校博士學科點專項科研基金(編號：20120143110005)。

陳梵(1993—)，男，碩士研究生，430070 湖北省武漢市洪山區珞獅路122號。