關于單色光帶寬對光度法測量的影響

邱德仁(復旦大學化學系，上海 200433)

?

關于單色光帶寬對光度法測量的影響

邱德仁*
(復旦大學化學系，上海 200433)

摘要：指出目前分析化學教科書中關于單色光帶寬對Beer定律影響的敘述有誤。綜述了光度法發展史，說明早在1954年Broderson已經給出了正確的論述。

關鍵詞：光度分析；光譜帶寬；Beer定律

光度法是分析化學教學中的一個基礎內容。光度法的一個必要條件是采用單色光。單色光的波長范圍即光譜帶寬對Beer定律的影響的內容在分析化學教科書中都有論述。但是，在我看來，目前教科書中的論述都有問題甚至有錯誤。為了把意見說明清楚，還須從光度分析法的發展歷史說起。

20世紀50年代，在二戰研發原子彈的背景下，分析化學中的原子光譜分析一枝獨秀，比色分析或光度分析尚處于幾個簡單的發色體系的狀況。使用的儀器是Duboscq目視比色計、Pulfrich目視比色計等。Duboscq 比色計有兩個液柱，分別盛參比液和被測液，以調節液柱高度(光程長)達到目測顏色一致的方法測量吸光度，光吸收用Lambert定律表征。Pulfrich光度計兩臂的液槽厚度(光程長)相同，以調節光的孔徑改變光強至兩邊目視顏色相同的方法測量吸光度，光吸收用Beer定律表征。此后兩個定律合并，稱為Lambert-Beer定律，簡稱Beer定律。實驗上，測得吸光度與吸光物質濃度呈線性關系即校準曲線成直線時，稱為遵守Beer定律。這兩種光度法的測量，單色光都采用濾光片獲得，根據互補色的原理選擇單色光波長，應用范圍局限于可見區。采用濾光片時，還沒有考慮過單色光的帶寬，以及帶寬對Beer定律的影響。

20世紀50年代出現了用硒光電池檢測光強的光度計，目視測量吸光度的主觀方法被光電池檢測的客觀方法代替，但單色光仍由濾光片提供。1940年，Beckman公司推出了第一臺分光光度計，采用棱鏡分光系統獲得單色光。這是光度法的一個里程碑。分光系統由入射狹縫-準直鏡-分光元件-聚光物鏡組成而獲得光譜焦面，安置在光譜焦面上的出射狹縫將選用波長的單色光隔離出來，供光度法測量。使用光電管或光電倍增管測量光強，光度法的光譜范圍又進一步從可見區擴展到紫外區。分光光度計的出現引起了與吸光度測量有關的問題：以一定機械寬度的出射狹縫隔離出來的單色光，它的波長范圍即光譜通帶寬度(簡稱光譜帶寬)是多少？帶寬的光譜分布怎樣？光譜帶寬跟測得的吸光度和Beer定律有什么關系？這些問題在20世紀五六十年代早已闡明，但遺憾的是，現在卻反而成為一個概念模糊甚至表述錯誤的問題。

在分光光度計商品儀器出現后的1954年，丹麥人Broderson[1]在美國光學學會期刊(J. Opt. Soc. Am.)上發表了一篇題為“Slit-width Effects”的文章，闡述分光系統狹縫寬度對所提供的單色光通帶的波長范圍和強度分布的影響，以及單色光帶寬與吸光度測量的關系。此后，Lothian[2]在他的專著《Absorption Spectrophotometry》中詳細引述并闡明了這些結論。主要是：

(1)當狹縫取共軛寬度(即入射狹縫和出射狹縫寬度相等)時，單色光呈三角形分布；以峰值強度之半所包括的波長范圍Δλ定義為帶通(俗稱半峰寬)；帶通等于狹縫機械寬度W 與光譜焦面的線色散率倒數 ( dλ/ dl )的乘積；通帶內的波長范圍為 2Δλ，在Δλ范圍內強度占總強度的75% (圖1)。

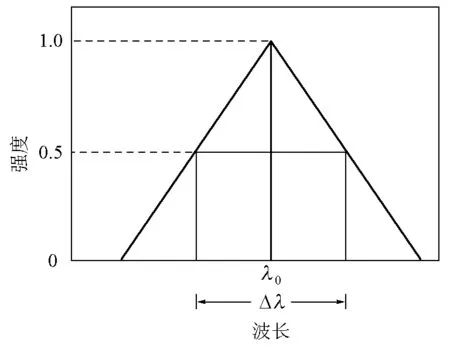
圖1　光譜通帶與分布

(2)測定得到的吸光度是通帶波長范圍內各波長吸光度的積分平均值。Broderson 計算了當單色光的通帶寬度Δλ與被測吸收光譜的寬度σ 以不同比例的條件測量時，得到測得的表觀吸光度與真實吸光度之間的關系如圖2所示。計算是在假定吸收峰呈Gauss函數形對稱分布、單色光呈三角形分布的情況下得到的。圖2表明，當單色光光譜帶寬無限小(即?λ/σ = 0)時，實測吸光度為真實吸光度，實測校準曲線與真實校準曲線重合；當單色光光譜帶寬與被測吸收峰寬度相等(即 ?λ/σ = 1)時，雖然實測校準曲線斜率比真實校準曲線斜率降低到約0.92倍，但在吸光度約小于0.8 的常用測定范圍內,比值仍保持恒定，即仍遵守Beer定律；在高吸光度范圍，比值偏離恒定，即偏離Beer定律(圖3)。單色光帶寬與被測吸收峰光譜寬度相等(即 ?λ/σ = 1)可以認為是遵守Beer定律的帶寬臨界條件。

由于光度法中通常吸收峰的半高峰寬約為數十納米，濾光片的光譜通帶寬度與其相當，因此采用濾光片做光度法測量時，偏離Beer定律并沒有被關注。實際上，Beer定律是在沒有考慮帶寬的條件下推導得到的。在此情況下僅考慮有色絡合物形成的化學因素對偏離Beer的影響。在用分光光度計測量時，采用的典型帶寬為納米級，偏離Beer定律的現象更不明顯。

在1958年Lothian[2]編著出版的《Absorption Spectrophotometry》中，詳細而完整地引述了這些結論。這本書可能是分光光度法早期最重要的專著。之后，在1961年廈門大學陳國珍[3]編著出版的《分光光度法》中，也引述了這些內容。至此，可以認為，關于單色光帶寬與吸光度測量的關系，以及帶寬與Beer定律的關系，已經有了明確的認識。

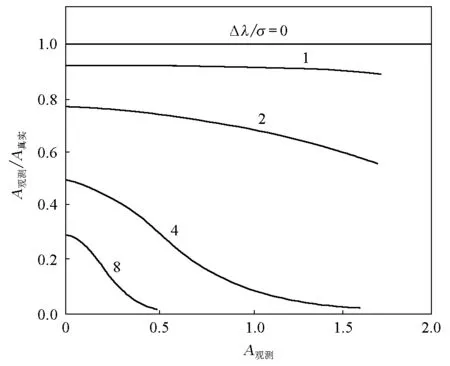
圖2　以不同光譜帶寬條件計算得到的實測吸光度與真實吸光度之比

圖3　真實校準曲線與實際觀測校準曲線的比較

但是，過了20年以后，到20世紀80年代初，出現了問題。1980年，上海科學技術出版社出版了Skoog 和West[4]的著作《Principles of Instrumental Analysis》的中譯本《儀器分析原理》。書中錯誤地把是否偏離真實吸光度作為是否偏離Beer定律的依據，而不是按照濃度與吸光度關系的校準曲線是否直線作為是否遵守Beer定律的依據。Skoog和West的書是在國內外都十分有影響的儀器分析教材。1983年，復旦大學出版社出版了朱世盛[5]的《儀器分析》，也引用了該書的這些不正確說法。由于20世紀60年代初，復旦大學朱世盛在國內率先開設了儀器分析基礎課和儀器分析實驗基礎課，故而復旦版《儀器分析》在國內有廣泛的影響，被后繼編寫、出版的教科書多次引用。這兩本書都把是否偏離真實吸光度作為是否偏離Beer定律的準則。Skoog 和West[6]在后來的修訂版中刪去了這些內容。朱世盛在書出版后不久也發現了問題，并希望在以后修訂版中更正。但是此后出版的分析化學教材，都仍以訛傳訛地出現了類似問題。

Broderson闡明的概念說明了分光光度計提供的帶寬為nm級的單色光不能用于共振線物理寬度為pm級的原子吸收光譜測量。1985年第一屆北京BCEIA 國際會議期間，我和Boumans 很有興趣地討論過原子吸收光譜的發展歷史。我們都認為，可以合理地推測，1954年Broderson 關于單色光帶寬與吸收峰寬度相等是光吸收遵守Beer定律臨界條件的論述，作為理論先導，促進了次年(1955年)澳大利亞人Walsh 和荷蘭人Alkemade 同時分別提出原子吸收光譜的銳線光源和峰值吸收原理，從而奠定了原子吸收光譜分析的理論基礎和實驗基礎。

致謝：復旦大學圖書館毛裕和及博士生張坤幫助查閱早年文獻資料，謹致謝意。

參 考 文 獻

[1]Broderson, S. J. Opt. Soc. Am. 1954, 44, 22.

[2]Lothian, G. F. Absorption Spectrophotometry, 2nd ed.; Adam Hilger Ltd.: London, 1958.

[3]陳國珍. 分光光度法. 北京: 科學出版社, 1961.

[4]斯科格, D. A.; 韋斯特, D. M. 分析化學原理. 吉林大學化學系分析化學教研室, 譯. 上海: 上海科學技術出版社, 1980.

[5]朱世盛. 儀器分析. 上海: 復旦大學出版社, 1983.

[6]斯科格, D. A.; 韋斯特, D. M. 分析化學原理. 第2版. 吉林大學化學系分析化學教研室, 譯. 上海: 上海科學技術出版社, 1987.

? 自學之友?

Effects of Spectral Bandwidth on Photometry Measurements

QIU De-Ren*
(Department of Chemistry, Fudan University, Shanghai 200433, P. R. China)

Abstract:An incorrect description about the effects of the spectral bandwidth on photometry measurements is presented in domestic analytical chemistry textbooks. In this paper, a review of photometry development history was given to show that Broderson had clarified the effects of spectral bandwidth in 1954.

Key Words:Photometry; Spectral bandwidth; Lambert-Beer law

*通訊作者，Email: qiu_deren@163.com

doi:10.3866/pku.DXHX20160164www.dxhx.pku.edu.cn

中圖分類號：O65；G64