斜拉橋施工參數敏感性分析

李夫凱, 張 力

(1.安徽省交通規劃設計研究總院股份有限公司，安徽 合肥 230088；2.合肥工業大學 土木與水利工程學院，安徽 合肥 230009)

斜拉橋施工參數敏感性分析

李夫凱1, 張 力2

(1.安徽省交通規劃設計研究總院股份有限公司，安徽 合肥 230088；2.合肥工業大學 土木與水利工程學院，安徽 合肥 230009)

在斜拉橋的施工過程中，存在很多不確定因素和不可避免的誤差，這些因素會影響橋梁施工控制精度，導致橋梁結構的成橋狀態與設計狀態不完全一致。在施工控制過程中，必須識別這些參數，分析這些參數可能引起的誤差，并進行調整和修正。通過某斜拉橋成橋狀態和設計狀態偏差的主要因素及其影響大小分析，望能對以后同類橋梁施工及施工管理提供微薄的參考價值。

斜拉橋；施工控制精度；成橋狀態；設計狀態

1 概 述

在斜拉橋的施工過程中，存在很多不確定因素和不可避免的誤差，這些因素會影響橋梁施工控制的精度，導致橋梁結構的實際狀態與設計狀態不完全一致[1-2]。造成橋梁結構實際狀態和設計狀態偏差的主要原因是實際施工過程中各項結構參數的變化，與設計狀態有一定偏差，另外施工誤差、測量誤差等也是重要的影響因素。設計參數包括自重、混凝土彈性模量、斜拉索彈性模量、斜拉索索力、溫度等[3-5]。在這些參數中，有些參數的改變會對橋梁結構產生較大的影響，稱之為敏感參數。有些參數的改變對橋梁結構的影響較小，稱之為非敏感參數[6-7]。參數敏感性分析的目的就是通過識別確認其中對橋梁結構影響較大的參數。根據設計參數的影響程度，一方面保證了施工的精確性，另一方面可以適當放寬對某些非敏感性參數的控制要求，減少人力物力[8]。

本文以某120 m+160 m獨塔雙索面斜拉橋為例進行分析，涉及敏感性分析的設計參數主要有：主梁自重變化、溫度變化、主梁混凝土彈性模量變化、索力偏差、預應力參數變化等。以成橋階段主梁變形與拉索內力作為控制目標。在進行參數敏感性分析時，一般只要使需要考察的參數變化一定幅度，其他參數采用設計時的基準值，在這個條件下考察控制目標的變化程度來判斷結構設計參數的敏感性，得到結果可以指導施工控制工作[8-9]。

2 主梁自重敏感性分析

模板變形、截面尺寸誤差、混凝土超方等都會引起結構自重的變化，因此在實際施工過程中主梁自重很容易產生偏差[7]。在保持模型其他參數不變的前提下，將主梁自重分別增加5%、10%，計算目標工況下主梁線形和內力變化，結果如圖1、圖2所示。

圖中數據均為目標值與基準取值的計算差值。

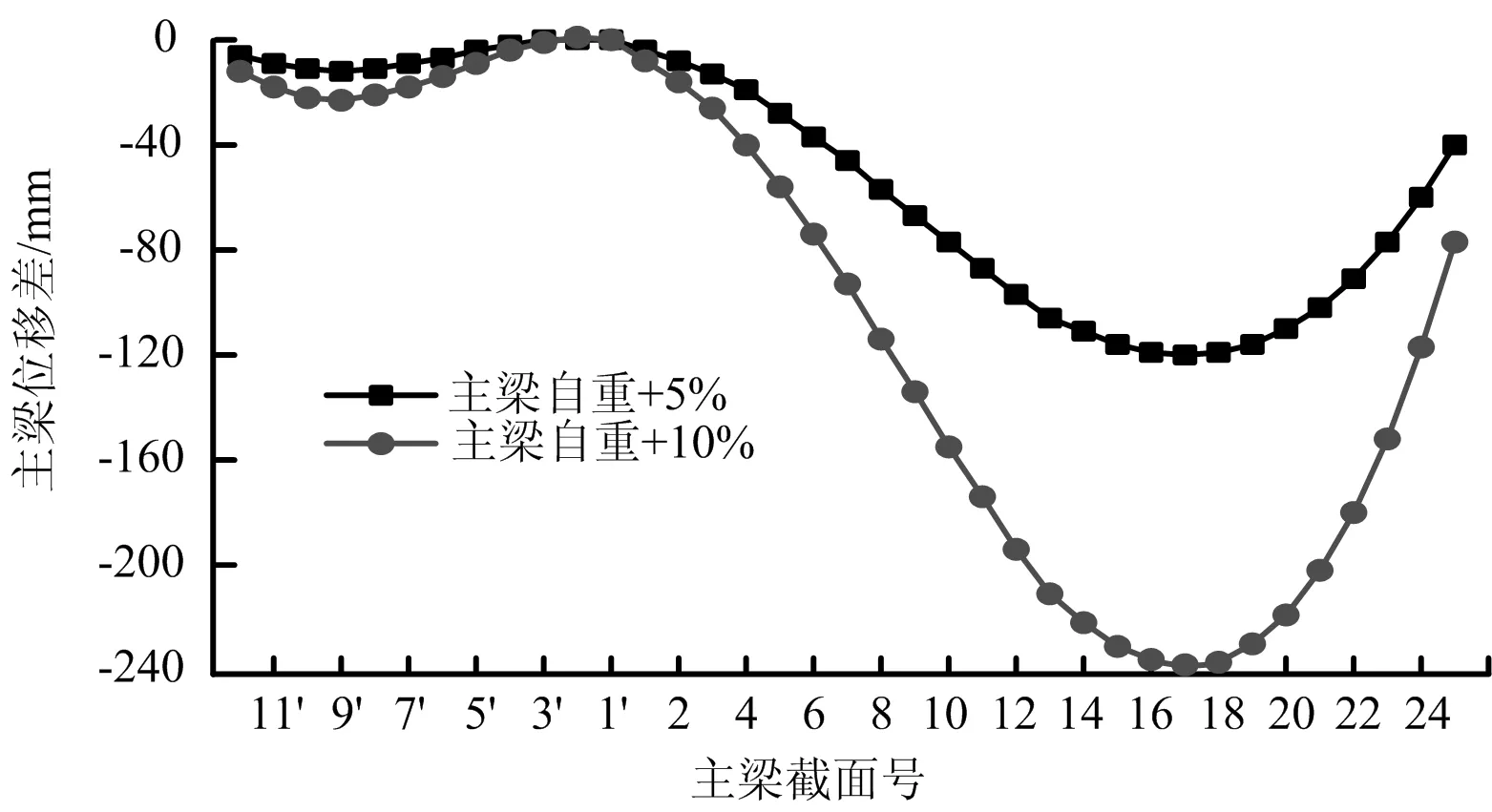
圖1 成橋階段主梁累計撓度變化值

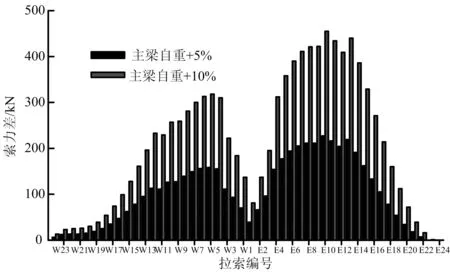
圖2 成橋階段拉索索力變化值

從圖1、圖2中可以看出成橋階段當主梁自重增加5%時最大撓度變化值最大達120 mm，自重增加10%時此處撓度變化值最大達238 mm；當自重增加5%時索力最大變化了227 kN(4.4%)，當自重增加10%時索力最大變化了455 kN(8.7%)。由此可見，主梁自重的變化對橋梁結構線形和內力的影響均十分顯著。

3 溫度敏感性分析

溫差可以分晝夜溫差和季節溫差兩種，晝夜溫差是結構局部溫差，季節溫差則是結構均勻性整體升溫或整體降溫[1,10]，下面分別對兩種溫差進行研究分析。

(1) 晝夜溫差敏感性分析。晝夜溫差的模擬可以通過軟件中的溫度梯度功能實現，在其他條件不變的前提下，設定主梁頂板溫度和底板溫度差分別為10 ℃，-10 ℃時，通過計算成橋狀態下主梁內力和線形的變化來判斷晝夜溫差的敏感性[4-6]。其結果如圖3、圖4所示。

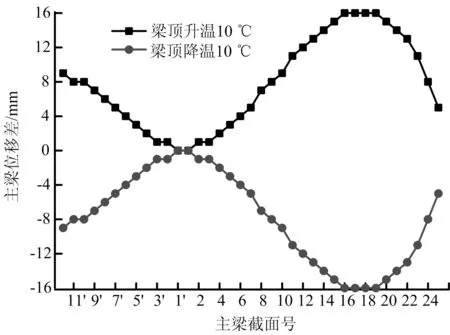
圖3 成橋階段主梁累計撓度變化值

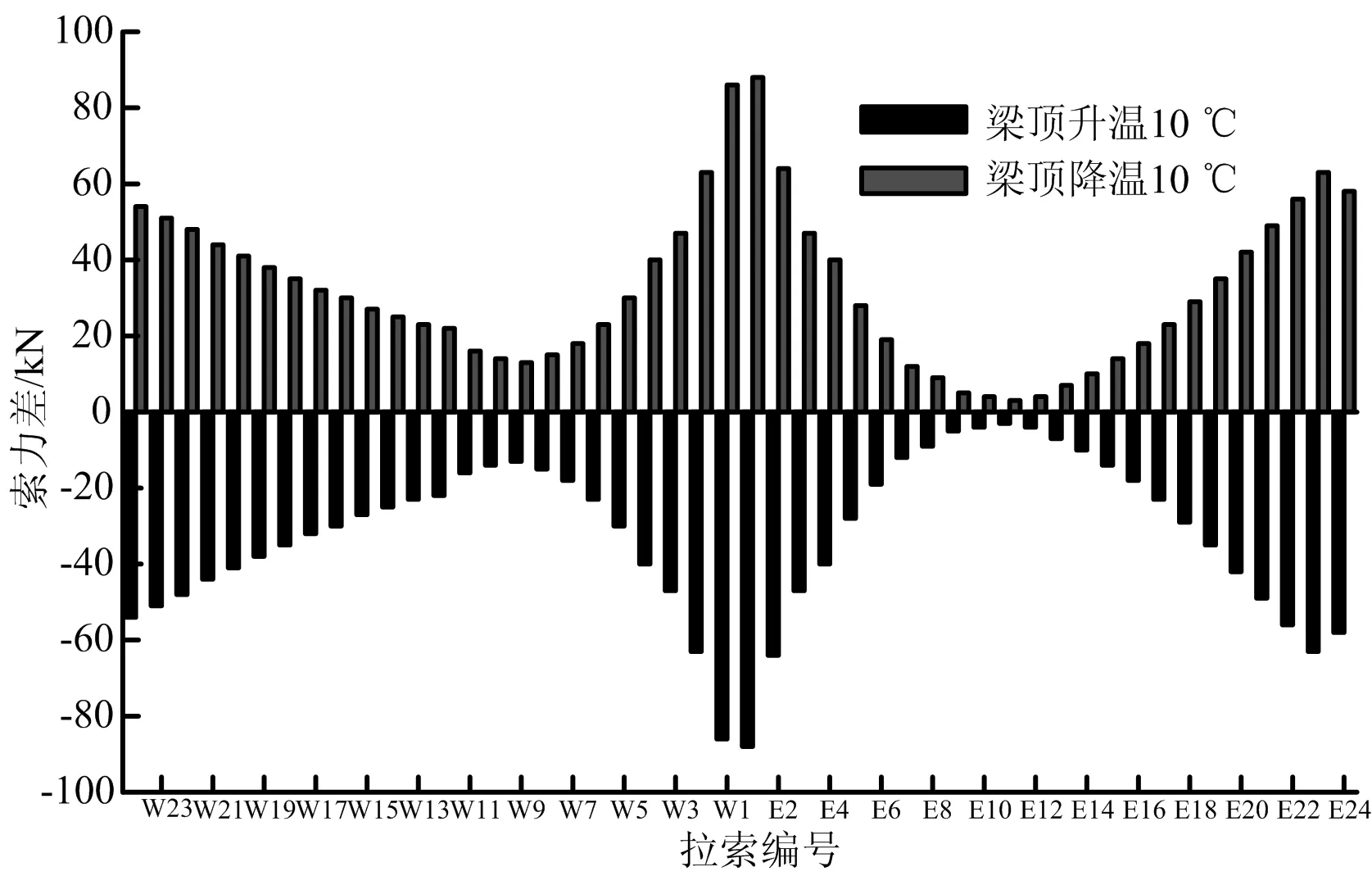
圖4 成橋階段拉索索力變化值

從圖3、圖4中可以看出，成橋階段晝夜溫差使得橋梁結構線形發生變化，其中變化最大為主跨跨中位置，差值為16 mm；晝夜溫差也使全橋索力發生一定變化，根部及兩端的拉索索力變化大于跨中位置，其中索力變化最大差值為88 kN(2.3%)，出現在主梁根部拉索區。由此可得，晝夜溫差對橋梁結構線形和內力有一定影響。

(2) 季節溫差敏感性分析。季節性溫差的模擬可以通過在模型中添加溫度荷載來實現。系統整體升溫按25 ℃考慮，系統整體降溫也按25 ℃考慮。通過計算模型成橋狀態下主梁內力和線形的變化來判斷季節性溫差的敏感性。其結果如圖5、圖6所示。

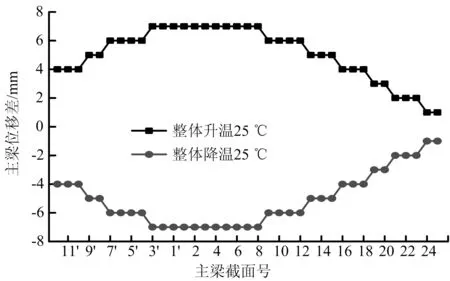
圖5 成橋階段主梁累計撓度變化值

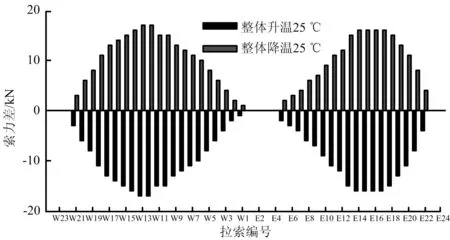
圖6 成橋階段拉索索力變化值

從圖5、圖6中可以看出，成橋階段季節性溫差使得橋梁結構線形發生變化最大為主梁根部位置，差值為7 mm；全橋索力變化最大為邊跨及主跨跨中位置，其中索力變化最大差值為17 kN(0.3%)。經過比較可知，季節性溫差對橋梁結構的影響明顯小于晝夜溫差產生的影響。季節性溫差對橋梁構的線形和內力影響比較小。

4 主梁彈性模量敏感性分析

橋梁在實際施工過程中由于各方面因素影響混凝土的彈性模量往往與設計值不相符[7，11]，為了研究其對橋梁結構的影響程度，下面主要列出主梁混凝土彈性模量增加5%和10%后目標工況下橋梁線形及受力性能的變化情況。如圖7、圖8所示。

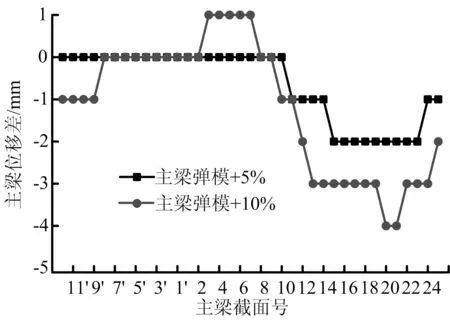
圖7 成橋階段主梁累計撓度變化值

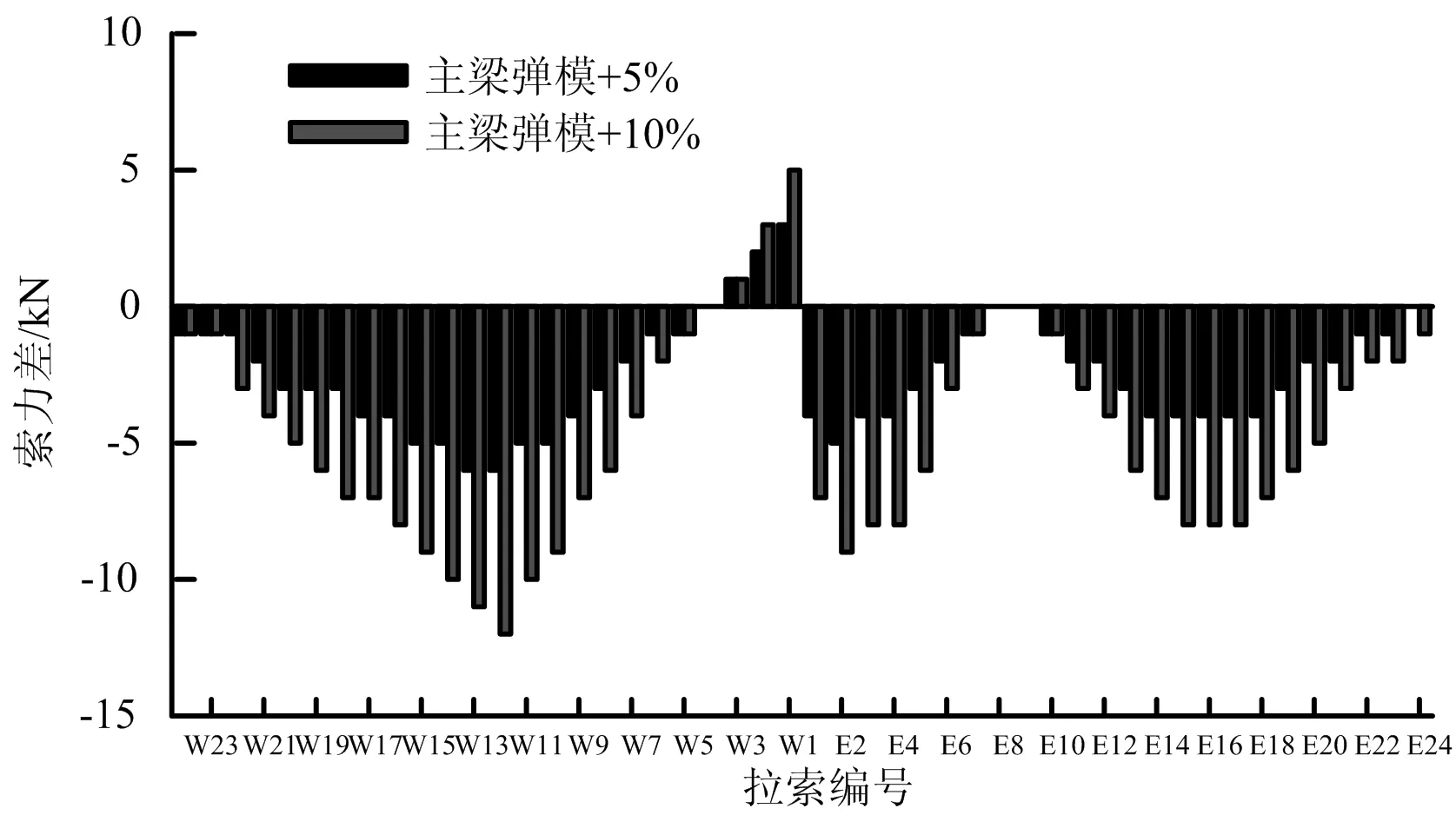
圖8 成橋階段拉索索力變化值

從圖7、圖8可以看出，主梁混凝土彈性模量增大10%時成橋階段撓度最大變化量只有4 mm，拉索索力最大變化量為12 kN(0.2%)。而主梁混凝土彈性模量增大5%時，其撓度、索力的變化量均為上述數值的一半。由此可得，主梁彈性模量的變化對全橋線形和受力性能的影響較小。

5 拉索索力敏感性分析

相比于其他類型橋梁，斜拉索在斜拉橋中承擔了相當大的荷載作用。而在施工中由于各種原因造型索力不同于計算索力幾乎每個橋都是，只是根據施工單位的責任態度不同，差別大小不同而已[2，7]。本文通過對模型中成橋索力值增大5%、10%的方式來分析索力對成橋狀態下線形的影響，其結果如圖9所示。

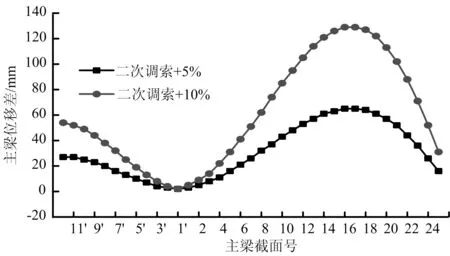
圖9 成橋階段主梁累計撓度變化值

從圖9中可以看出，成橋索力增大5%時，主梁撓度最大變化量達61 mm，成橋索力增大10%時，主梁撓度最大變化量達128 mm，由此可得，斜拉索索力對橋梁結構的線形影響顯著。

因此，在每個施工階段，都要加大對索力的實時監控工作，根據設計要求嚴格控制二次調索過程中的索力大小，減小索力誤差給橋梁結構帶來的不利影響，以保證橋梁結構最終線形和內力合理。

6 預應力敏感性分析

預應力參數主要包括預應力與管道壁的摩擦系數，管道每米局部偏差影響系數，錨具變形、鋼筋回縮和接縫壓縮值等[4-5]，這些參數的設計基準值分別為0.17、0.001 5 m-1、0.006 m。實際施工中這些參數很難與理論值保持完全一致，特別在管道彎曲半徑上，施工單位往往不按照設計半徑設置，而是根據方便隨意彎折了事，對預應力損失影響較大。因此本文通過對這三個參數分別增大5%、10%后成橋階段主梁撓度、索力的變化情況來判斷其敏感性，結果如圖10、圖11所示。

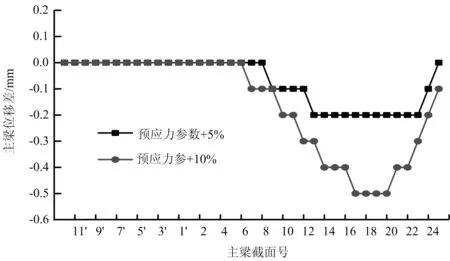
圖10 成橋階段主梁累計撓度變化值

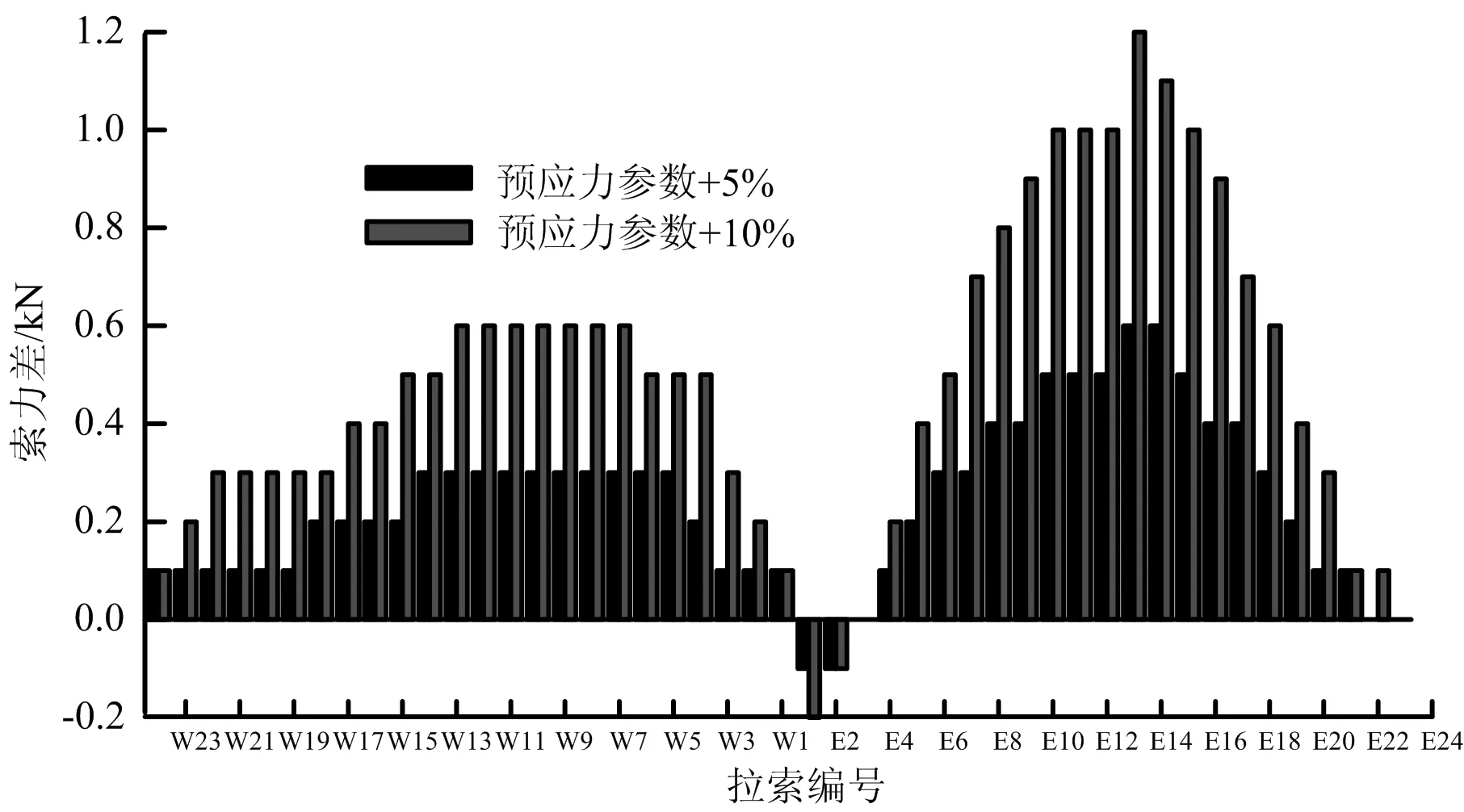
圖11 成橋階段拉索索力變化值

從圖10、圖11中可以看出，將預應力三個參數增大10%時，主梁撓度最大變化量只有0.5 mm，拉索索力最大變化量只有1.2 kN。由此可得，主梁預應力參數的變化對橋梁成橋狀態時的線形和內力并無明顯影響。

7 參數敏感性結果分析

前面已分析了主梁自重、晝夜溫差、季節性溫差、混凝土彈性模量、索力、預應力參數對主梁成橋階段的線形和索力的影響。現將各參數影響程度進行排序。表1、表2文中分析了參數變化5%和10%后的情況，為便于比較，均選取參數變化10%后對成橋階段的影響。并且基于該變量絕對值的大小對參數敏感性進行排序[12]。

表1 主梁線形各影響因素敏感程度排序

表2 拉素索力各影響因素敏感程度排序

8 結束語

本文以成橋階段主梁變形、拉索索力作為控制目標。對主梁自重、溫度、主梁彈性模量、索力、預應力參數5個參數的敏感性進行了分析。并根據分析結果將各參數對主梁線形、索力的影響程度進行排序。經過分析可知，對斜拉橋成橋安全度敏感性程度較大的參數是主梁自重、拉索索力[12]、晝夜溫差等。因此、施工單位在施工中應嚴格對這些因素進行控制，管理單位可根據敏感因素的敏感程度采取針對性管理策略，以求達到更好的成橋狀態。

[1] 匡樹鈞.斜拉橋施工監控技術[J].山西建筑，2008,34(8):333～334.

[2] 郝中海.五河口斜拉橋施工質量監理[M].北京：人民交通出版社，2009.

[3] 王 君.大跨度預應力混凝土連續梁橋施工監控與結構仿真分析[D].合肥：合肥工業大學，2012.

[4] 顧安邦,范立礎.橋梁工程(下冊)[M].北京：人民交通出版社，2005.

[5] 項海帆.高等橋梁結構理論[M].北京：人民交通出版社，2002.

[6] 劉旭政,黃平明,許漢錚.獨塔斜拉橋參數敏感性分析[J].長安大學學報(自然科學版)，2007,27(6):63～66.

[7] 中交第二航務工程局有限公司.斜拉橋——公路橋梁施工系列手冊[M].北京：人民交通出版社，2014.

[8] 張自榮，薛 進.斜拉橋施工監理技術[M].北京：人民交通出版社，2010.

[9] 岳東杰.現代大型斜拉橋塔梁施工測控技術[M].北京：科學出版社，2012.

[10] 完海鷹,許利星,馬慶宏.單索面矮塔斜拉橋結構設計參數敏感性分析[J].工程與建設,2012,26(3):349～351.

[11] 王 濤.矮塔斜拉橋的施工監控技術研究[D].合肥：合肥工業大學,2012.

[12] 續若楠.矮塔斜拉橋施工控制與索力優化研究[D].南京：東南大學，2011.

2016-09-07；修改日期：2016-09-09

李夫凱(1984-)，男，安徽合肥人，碩士，安徽省交通規劃設計研究總院股份有限公司工程師．

U448.27

A

1673-5781(2016)05-0689-04