二維機織復合材料力學分析中的周期性邊界條件研究

薛亞紅， 陳繼剛， 閆世程， 駱俊廷

(1. 燕山大學 機械工程學院， 河北 秦皇島 066004； 2. 燕山大學 自潤滑關節軸承共性技術航空科技重點實驗室，河北 秦皇島 066004； 3. 燕山大學 先進鍛壓成形技術與科學教育部重點實驗室， 河北 秦皇島 066004)

二維機織復合材料力學分析中的周期性邊界條件研究

薛亞紅1，2， 陳繼剛1，2， 閆世程1，2， 駱俊廷1,3

(1. 燕山大學 機械工程學院， 河北 秦皇島 066004； 2. 燕山大學 自潤滑關節軸承共性技術航空科技重點實驗室，河北 秦皇島 066004； 3. 燕山大學 先進鍛壓成形技術與科學教育部重點實驗室， 河北 秦皇島 066004)

為了精確地進行二維機織復合材料力學性能的數值分析,需建立單胞模型的準確邊界條件。基于周期邊界條件理論，提出了簡便通用的二維機織復合材料周期邊界方程，并給出了周期邊界條件下各彈性常數在有限元分析中的求解方法；為驗證周期邊界條件的正確性，建立了9個單胞構成的九宮格結構，取中央單胞作為參考單胞，對不同邊界條件下獨立單胞的變形和應力分布與參考單胞進行對比。研究結果表明：即使在單向拉伸載荷下，單胞各個邊界面也不保持平面狀態，而是出現凹凸翹曲變形，即存在邊界周期性；通過邊界周期性條件，可正確地獲得二維機織織物的工程彈性常數。

二維機織復合材料； 周期邊界條件； 單胞； 有限元模型； 彈性常數

二維機織復合材料是一種新型輕質高效結構材料，具有質量輕，抗沖擊性好，比強度和比剛度高等優點，被廣泛應用于航空航天、國防、電力、醫藥和紡織等領域[1]。對于二維機織復合材料綜合力學性能的預測是其用于結構設計的重要前提。織物復合材料在結構上一般呈現良好的周期性，通常基于單胞計算分析其宏觀力學性能[2]，主要包括理論解析法和有限元計算法。理論解析法基于等應力或應變假設，按所占的體積分數加權平均組分材料剛度矩陣來得到織物總體的等效剛度。它能很好地預測織物的宏觀力學性能，但不能得到材料細觀層次上的應力分布。有限元計算法通過建立織物的單胞模型，并施加一定的邊界條件，即可得到材料細觀層次的應力應變分布及宏觀力學性能，因此受到眾多學者的青睞。

基于單胞的織物有限元分析中，合理的邊界條件是保證計算準確的關鍵。目前普遍假設邊界面保持一致[3]，即約束一個面的法向，對其對立面施加荷載，而其他面進行法向耦合使其保持平面。這種邊界條件在有限元計算中很方便施加，但形成了過約束，破壞了相鄰單胞邊界面上應力的連續性，僅適用于單向載荷狀態具有反對稱結構的單胞[4-5]。Hori等[6]研究結果表明：等應變假設的邊界條件將得到織物彈性常數的上限，應力連續性難以滿足；等應力假設的邊界條件將得到織物彈性常數的下限，不能滿足相鄰單胞變形的連續。為此，文獻[7]通過建立多個單胞來減小邊界效應，雖然能獲得較好的結果，但大大降低了計算效率。

Whitcomb[8]、Xia[9]提出了周期邊界條件理論，較精確地獲得了織物的力學性能。Li[10]、Xu[11]、Carvalho[12]根據所研究織物的具體結構，給出了各種單胞下周期邊界的表達形式，雖然較好地預測了織物的力學性能，但這些表達式均需事先給定單胞的平均應變，通過有限元模擬得到相應的應力。而工程上通常在已知載荷的情況下，用簡單拉伸及剪切實驗測量試件的位移，求得工程彈性常數。另外，周期邊界方程依賴于單胞的選取、織物的結構及受載情況。文獻[13]利用對稱和反對稱性，將單胞簡化為1/16單胞模型，在降低計算量的同時，極大地增加了周期性邊界條件的施加難度；張超等[14]介紹了三維織物復合材料的周期邊界方程及彈性常數求解方法，但并不適用于只具有2對周期邊界的二維機織物。文獻[15]將三維周期性邊界表達式應用在具有二維機織復合材料上，將非周期性邊界面施加周期邊界方程，與實際并不相符。

為此，本文給出了一種對于二維機織復合材料通用而簡便的周期邊界方程，通過建立多個單胞組成的九宮格結構，取中間單胞以減小邊界效應的方法，驗證周期邊界方程的準確性。

1 周期邊界條件理論

織物復合材料在結構上一般具有周期性，只需進行平移而不需要旋轉就能形成整個織物結構的最小重復單元，稱為單胞。圖1示出具有周期性結構的織物胞體二維示意圖。

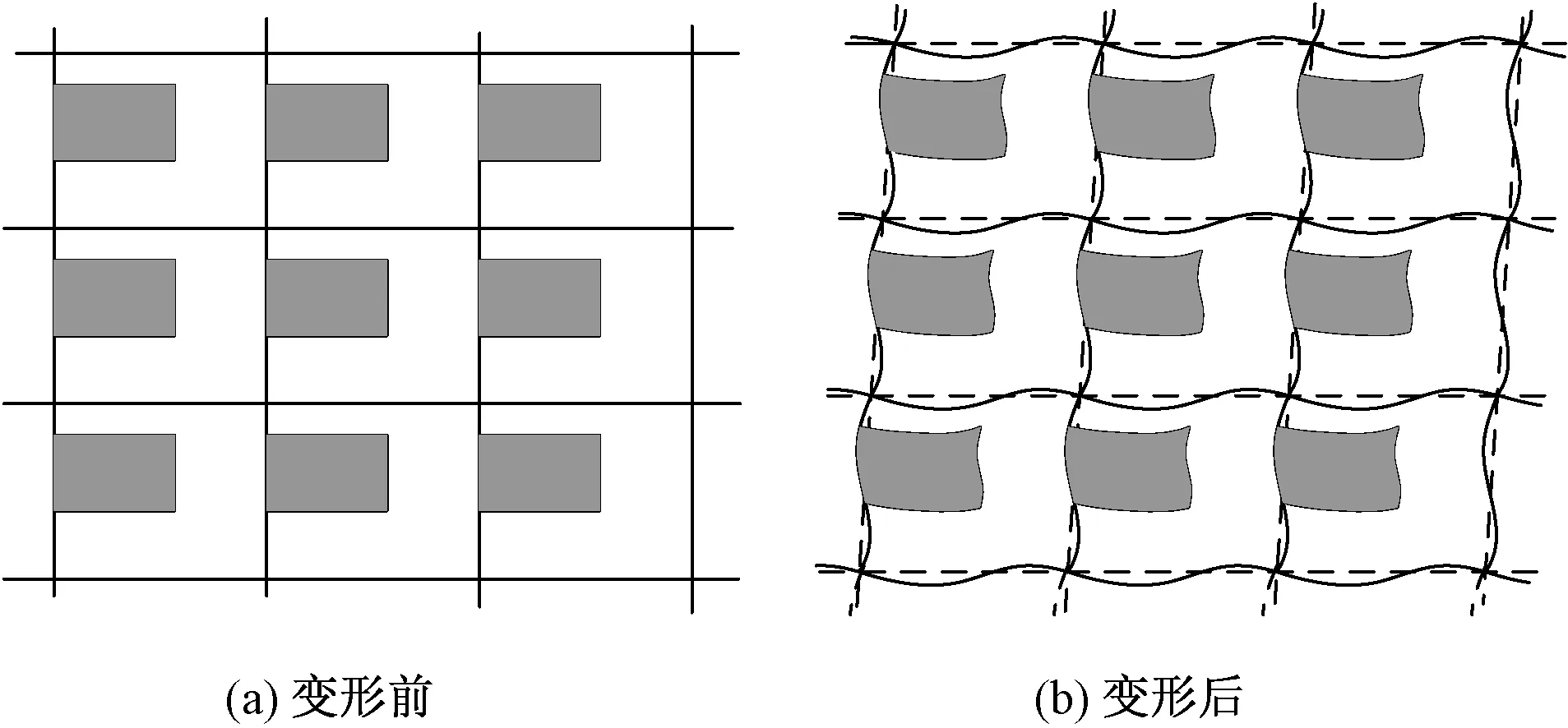
圖1 具有周期性結構的織物胞體二維示意圖

胞體內任意點的位移場[9]可表示為

(1)

(2)

(3)

式中：k+和k-分別表示法向沿Xk正負2個方向的周期邊界面。

(4)

(5)

從式(5)可以看出，方程滿足邊界上位移的周期性與連續性，并且平行的周期邊界面上對應節點的位移差保持為常數。Xia等[9]還進一步證明施加式(5)后相鄰單胞邊界處能夠同時滿足應力的連續性，因此可采用式(5)對單胞進行分析。

2 周期邊界條件有限元分析模型

2.1 單胞分析模型

斜紋織物襯墊為典型的具有二維周期性結構的機織復合材料。圖2示出一上二下左斜紋織物的細觀結構三視圖。圖中虛線部分為其單胞，沿著2個編織方向，單胞結構上具有周期性。為分析方便，建立了織物單胞坐標位置圖，如圖3所示。單胞在坐標系中位置為0≤x≤2a，0≤y≤2b，0≤z≤2c，坐標原點建立在點D，2對周期邊界面分別沿x軸和z軸，織物厚度方向沿著y軸，結構上不具有周期性。

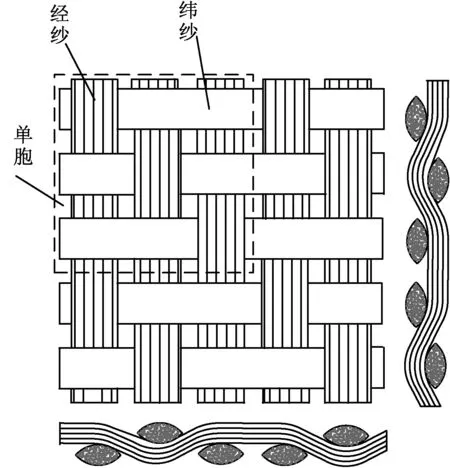
圖2 斜紋織物的細觀結構三視圖

圖3 織物單胞坐標位置圖

2.2 有限元力學分析的周期邊界條件設定

2.2.1 剛體位移約束

為了消除單胞剛體位移，選擇頂點A、D、C、H，約束式(6)中的6個自由度。

(6)

式中：U、V、W分別表示沿x、y、z方向的位移；下標字

母表示頂點處的節點；下標數字表示棱邊上的節點；下標為等式則表示對應面上的節點。

2.2.2 面上節點約束

在2對平行的周期邊界面中，分別選擇x=0與z=0的面為主平面，與主平面相對的面為從平面，主平面上的節點為主節點，從平面上的節點為從節點。選擇節點對(D，C)，(D，A)作為參考，由式(5)可知，對于法向沿x方向的對應主節點與從節點，其位移差即為節點C與D的位移差。由于節點D固定，位移差即為節點C的位移。同理，法向沿z方向的主節點與從節點的位移差，即節點A的位移。

法向沿x軸的面內節點約束：

(7)

法向沿z軸的面內節點約束：

(8)

連續體沿y軸方向的結構不具有周期性，因此，法向沿y軸的面不需要施加周期邊界約束。

2.2.3 棱邊節點約束

對于自由的4個頂點(B、E、F、G)和4個棱邊(9，10，11，12)，處于兩周期邊界面的交界處，其節點同時滿足式(7)、(8)，如果直接把這些約束都施加到有限元分析中，就會導致有些節點既為主節點，又為從節點，計算將無法進行，因此，需將這些棱邊和頂點單獨施加相互獨立的方程。

以棱9為參考，對于棱10，只施加方程(7)，其節點約束為

(9)

對于棱12，只施加方程(8)，其節點約束為

(10)

對于棱11，由式(7)、(8)可得其節點約束為

(11)

(12)

2.2.4 頂點約束

以頂點D為參考，對于頂點G，只施加方程(7)，其節點約束為

(13)

對于頂點E，只施加方程(8)，其節點約束為

(14)

對于頂點F，由式(7)、(8)可得其節點約束為

(15)

以頂點D為參考，對于頂點B，其節點約束為

(16)

式(6)～(16)，可應用有限元分析軟件中的邊界設定，利用其多點約束功能并結合編寫的相應程序加以實現。

3 周期邊界下織物彈性常數求解方法

3.1 宏觀彈性常數求解方法

在利用細觀有限元法研究二維機織復合材料宏觀力學性能時，施加周期邊界條件的目的，僅僅保證

可以用1個單胞代替整個織物的建模，如通過單胞研究織物的宏觀彈性常數進行強度預測等。欲求得織物的宏觀力學性能，需要在周期邊界條件的基礎上，施加一定的載荷。二維機織復合材料為各項異性材料，其等效本構方程可記為

(17)

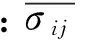
(18)

式中：Ex、Ey、Ez分別為二維機織復合材料在x、y、z方向的彈性模量；Gxy、Gyz、Gxz分別為xy、yz、xz面內的剪切模量；μxy、μyz、μxz、μyx、μzy、μzx分別為xy、yz、xz、yx、zy、zx面內的泊松比。若要得到織物的9個工程彈性常數，可以施加6組線性不相關的宏觀應力場。周期邊界條件下的6組簡單宏觀應力場如表1所示。

表1 周期邊界條件下的6組簡單宏觀應力場Tab.1 Six groups of simple macroscopic stress fieldparameters under periodic boundary condition

施加表1所示的1種應力場，可得到1個或多個二維機織復合材料的宏觀彈性常數。施加全部6種應力場，即可得到織物全部9個宏觀彈性常數。如施加k=1的應力場，可求得Ex、μxy、μxz。

(19)

3.2 周期邊界條件下的加載方法

對單胞施加周期邊界方程后，對于表1中的6組宏觀應力場，只需分別對6個節點自由度施加相應的集中力。

(20)

式中Fx|C為在頂點C施加x軸方向的集中力。

通過有限元后處理，由節點位移求得連續體宏觀平均應變值。

(21)

周期邊界條件下，二維機織復合材料宏觀彈性常數的具體求解方法為：首先在單胞模型的周期邊界面施加周期邊界方程(6)～(16)，然后給定表1所示的其中1種或幾種宏觀應力場，按照式(20)的載荷施加方式對節點施加集中力，計算后通過式(21)獲得宏觀平均應變值，最后由式(19)獲得織物宏觀彈性常數。

由于單胞y=0及y=2b的2面為非周期邊界面，未對節點進行關聯約束，因此，對于k=2及k=5的應力場，為避免應力集中，在施加集中力前，先將2面內的節點進行耦合處理。對于k=2的應力場：需將面y=2b內部(不包括4個棱邊和4個頂點)的所有節點與頂點H進行y方向的耦合，將面y=0內部的所有節點與頂點D進行y方向的耦合。對于k=5的應力場：需要將面y=2b內部的所有節點與頂點H進行z方向的耦合；將面y=0內部的所有節點與頂點D進行z方向的耦合。

4 實例驗證

4.1 周期邊界效應存在性驗證

為驗證周期邊界效應的存在，進行了斜紋織物襯墊壓縮實驗。斜紋織物襯墊由美國杜邦公司提供，其由徑向芳綸和緯向PTFE纖維編織而成，基體為酚醛樹脂。試件尺寸為100 mm×50 mm×0.4 mm，壓縮實驗在TOX電子壓機上進行，壓縮方向為垂直纖維編織方向，載荷為75 MPa。圖4示出顯微鏡下斜紋織物襯墊壓縮前后細觀結構圖。可以看出，斜紋織物襯墊經壓縮后，由于斜紋織物的細觀組織結構的不對襯，單胞的邊界面變形不一致，明顯看出徑向纖維束由直線狀經過壓縮出現屈曲變形，且這種變形形態存在重復性和周期性。

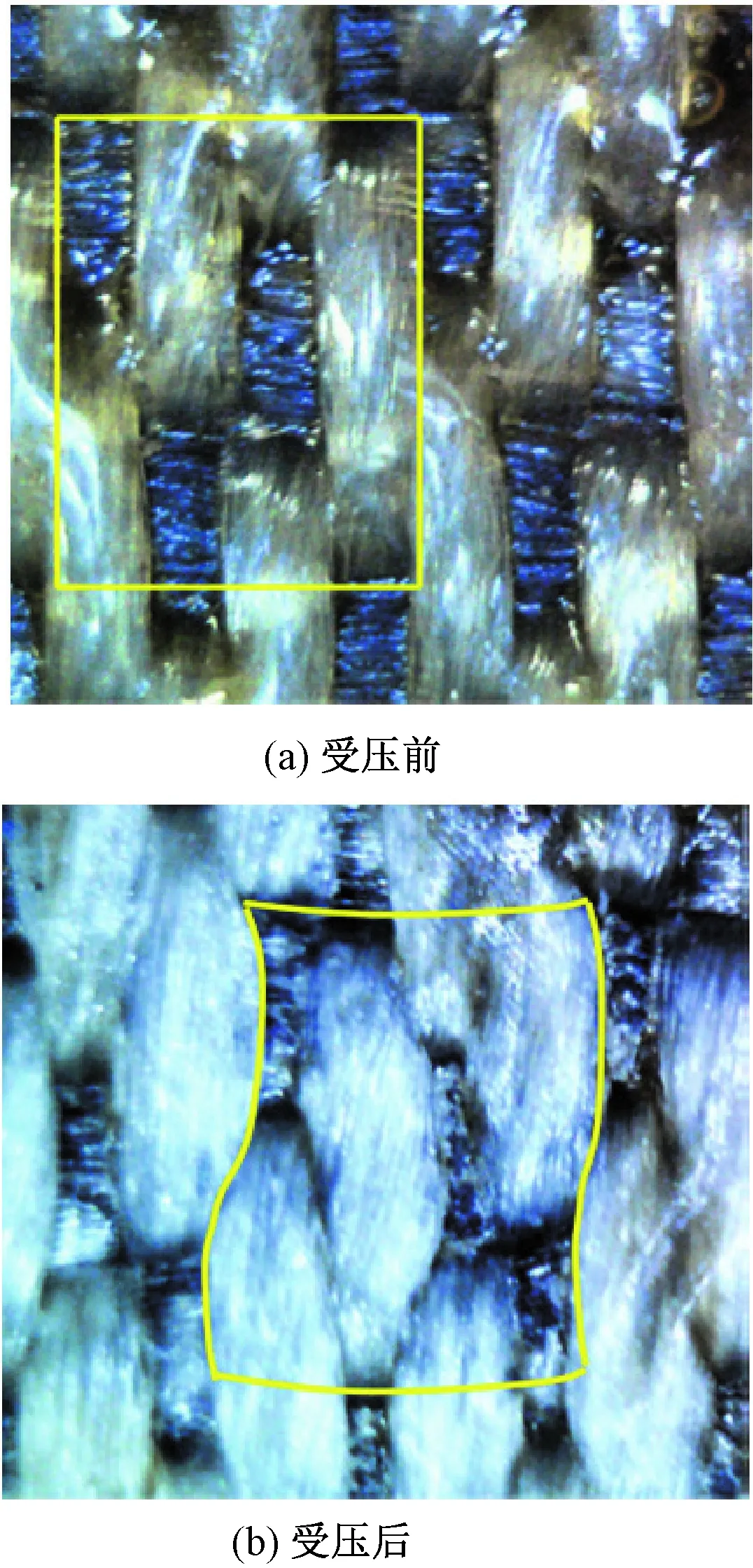
圖4 二維織物襯墊的受壓前與受壓后對比圖

4.2 周期邊界條件設置的正確性驗證

為驗證周期邊界條件設置的正確性，以斜紋織物為對象，進行力學性能的有限元模擬及實驗。其試件材料及尺寸同襯墊壓縮實驗，力學性能實驗在微機控制電子式萬能試驗機上進行。圖5示出斜紋織物的單胞的幾何模型。建立了如圖6所示的由9個單胞組成的九宮格結構，其中間單胞邊界效應較小，作為參考單胞。

以施加x方向的單軸拉伸為例，對于不同的胞體載荷施加方式為：1) 按照邊界保持一致的假設對九宮格結構施加約束。即固定ADEH面，使其法向位移為0；對CDHG、ABFE這2個邊界面施加法向耦合約束，使其法向變形保持平面；在BCGF面上施加沿x方向、大小為150 N的單向拉力。2) 按照本文方法對單胞施加周期邊界方程后，在單胞的節點C施加大小為50 N的集中力。3) 按照邊界保持一致的假設對單胞施加約束后，在BCGF面上施加沿x方向大小為50 N的單向拉力。圖7示出不同邊界下胞體的變形形態。

圖5 斜紋織物單個胞體的幾何模型

圖6 九宮格結構中參考單胞分析示意圖

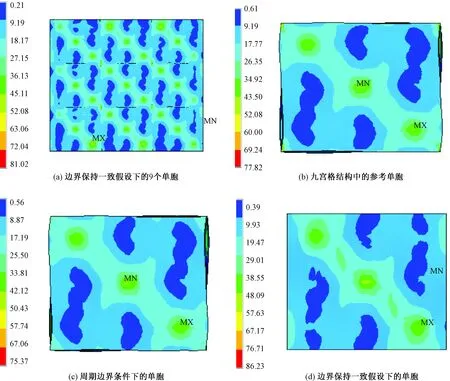
圖7 不同邊界條件下胞體的等效應力圖

從圖7可看出，由于邊界效應的影響，九宮格結構中沿x軸方向排布的3個單胞應力分布各不相同。周期邊界條件下的單胞變形形態與參考單胞的基本一致。此外，由于結構的不對稱性，即使在單向應力狀態下的邊界面也不再保持平面，而是出現了翹曲，但平行的周期邊界面保持相同的形狀變形，其位移差相等，從而保證了相鄰單胞位移的連續性。周期邊界下的單胞與參考單胞，應力分布有較小偏差，這是由于對九宮格結構施加了簡化的邊界條件，參考單胞受到一定的邊界效應的影響，并不能模擬連續體真實的周期性狀態。從圖5可看出，在平面保持一致的假設下單胞的等效應力整體偏大，這是由于邊界面保持一致，相當于施加了附加力，一定的載荷下變形減弱，使得單胞整體剛度增加。

表2給出了不同邊界條件下有限元模擬與實驗獲得的部分彈性常數值。可以看出，周期邊界條件下的彈性常數值與實驗結果較為接近，其預測的斜紋織物彈性模量誤差能控制在6%以內；由于單胞邊界面在變形過程中被迫保持為平面狀態，使得邊界保持一致假設下單胞的彈性常數預測值偏大，這與前面的分析一致。因此，基于本文給出的周期邊界條件的設置方法對預測二維織物復合材料的彈性常數有足夠的精度，及相對于傳統邊界保持一致的邊界條件設置方法具有絕對的優勢。

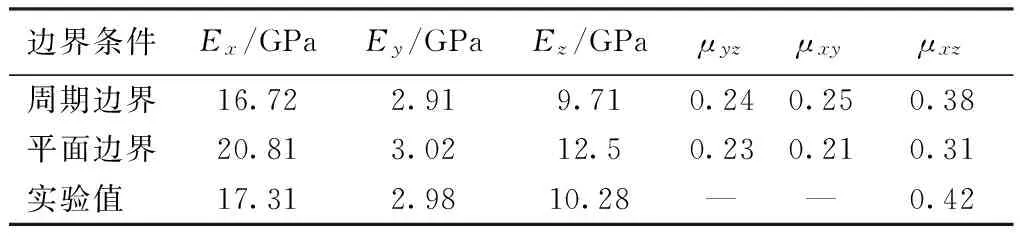
表2 不同邊界條件下有限元模擬值與實驗結果比較

5 結 論

本文針對二維機織復合材料的有限元分析模型問題，開展了單胞模型周期邊界條件的研究，得出了具有二維周期性結構的機織復合材料單胞的周期邊界方程，給出了在有限元中織物宏觀彈性常數求解方法。通過斜紋織物壓縮實驗，證實了織物周期邊界效應的存在。將九宮格結構的中央單胞作為參考單胞，對比不同邊界條件下單胞變形和應力分布，并進行斜紋織物彈性常數預測的模擬和實驗，證明了本文給出的單胞模型周期邊界條件的正確性。研究表明，織物復合材料的單胞即使在單向拉伸載荷下各個邊界面也不保持平面狀態，而是出現凹凸翹曲變形，即存在邊界周期性；本文給出的邊界周期性條件，相對于傳統有限元方法預測二維機織復合材料彈性常數有更高的精度。

FZXB

[1] QIU M, MIAO Y W, LI Y C, et al. Film-forming mechanis ms for self-lubricating radial spherical plain bearings with hybrid PTFE/aramid fabric liners modified by ultrasonic [J]. Tribology International, 2015(87): 132-138.

[2] BARBERO E J, TROVILLION J, MAYUGO J A, et al. Finite element modeling of plain weave fabrics from photomicrograph measurements [J]. Composite Structures, 2006, 73(1): 41-52.

[3] 張賦, 李旭東. 織物增強復合材料彈性常數的有限元法預測 [J]. 機械工程材料, 2014, (4)38: 82-86. ZHANG Fu, LI Xudong. Finite element prediction of elastic constant of fabric reinforced composites [J]. Materials for Mechanical Engineering, 2014, 38(4): 82-86.

[4] NEEDLEMAN A, TVERGAARD V. Comparison of crystal plasticity and isotropic hardening predictions for metal-matrix composites [J]. ASME Journal of Applied Mechanics, 1993,60(1): 70-76.

[5] SUN C T, VAIDYA R S. Prediction of composite properties from a representative volume element [J]. Composites Science and Technology, 1996, 56(2):171-179.

[6] HORI M, NEMAT-NASSER S. On two micromechanics theories for determining micro-macro relations in heterogeneous solids[J]. Mechanics of Materials, 1999, 31(10): 667-682.

[7] FANG Z, YAN C, SUN W, et al. Homogenization of heterogeneous tissue scaffold: a comparison of mechanics, asymptotic homogenization, and finite element approach [J]. Appl Bionics Biomech, 2005, 2(1): 17-29.

[8] WHITCOMB J D, CHAPMAN C D, TANG X D. Derivation of boundary conditions for micromechanics analysis of plain and satin weave composites [J]. Journal of Composite Materials, 2000, 34(9): 724-747.

[9] XIA Z H, ZHOU C W, YONG Q L, et al. On selection of repeated unit cell model and application of unified periodic boundary conditions in micromechanical analysis of composites [J]. International Journal of Solids and Structures, 2006, 43(2): 266-278.

[10] LI S G, WONGSTO A. Unit cells for micromechanical analyses of particle-reinforced composites [J]. Mechanics of Materials, 2004,36(7): 543-572.

[11] XU K, XU X W. Finite element analysis of mechanical properties of 3D five-directional braided compo-sites [J]. Materials Science and Engineering A, 2008(487): 499-509.

[12] CARVALHO N, PINHO S, ROBINSON P. Reducing the domain in the mechanical analysis of periodic structures, with application to woven composites [J]. Composites Science and Technology, 2011, 71(7): 969-979.

[13] LI S, ZHOU C, YU H, et al. Formulation of a unit cell of a reduced size for plain weave textile composites [J]. Computational Materials Science, 2011(50):1770-1780.

[14] 張超, 徐希武, 嚴雪. 紡織復合材料細觀力學分析的一般性周期性邊界條件及其有限元實現 [J]. 航空學報, 2013,34(7):1636-1645. ZHANG Chao, XU Xiwu, YAN Xue. General periodic boundary conditions and their application to micromech-anical finite element analysis of textile composite [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1636-1645.

[15] BAKAR I A A. KRAMER O, BORDAS S, et al. Optimization of elastic properties and weaving patterns of woven composites [J]. Composite Structures, 2013, 100(5): 575-591.

Periodic boundary conditions for mechanical property analysis of 2-D woven fabric composite

XUE Yahong1，2, CHEN Jigang1，2, YAN Shicheng1，2, LUO Junting1,3

(1.SchoolofMechanicalEngineering,YanshanUniversity,Qinhuangdao,Hebei066004,China; 2.AviationKeyLaboratoryofScienceandTechnologyonGenericTechnologyofSelf-LubricatingSphericalPlainBearing,YanshanUniversity,Qinhuangdao,Hebei066004,China; 3.KeyLaboratoryofAdvancedForging&StampingTechnologyandScience,MinistryofEducation,YanshanUniversity,Qinhuangdao,Hebei066004,China)

In order to accurately implement the numerical analysis for the mechanics performance of two-dimensional (2-D) woven fabric composite, the accurate boundary condition of unit cell model should be established. Based on the periodic boundary condition theory, a set of simple and universal periodic boundary equations was proposed for the 2-D woven fabric composite, and the solving method of elastic constants for engineering in the finite element analysis under the periodic boundary conditions was given. In order to verify the correctness of periodic boundary conditions, the nine-block-box structure including 9 unite cells of 2-D fabric composite were established. Taking the central cell as the reference cell, the deformation and stress distribution of the single cells under different boundary conditions were compared with the reference cell. The results indicate that all boundary surfaces of the fabric composite do not keep planar state, but present the concave and convex buckling deformation under uniaxial tensile load. In other words, the periodic property of the unite cell boundary faces is demonstrated. Furthermore, the engineering constants of the 2-D woven fabric composite can be obtained properly under the periodic boundary conditions.

2-D woven fabric composite; periodic boundary condition; unit cell; finite element model; elastic constant

10.13475/j.fzxb.20150800808

2015-08-05

2016-03-10

國家科技支撐計劃資助項目(2014BAF08B03)

薛亞紅(1989—)，女，碩士生。研究方向為自潤滑材料、精密成形。陳繼剛，通信作者，E-mail:24000082@qq.com。

TB 332

A