固定錐形閥消能設施消能效果的數值模擬研究

蘇克巴圖，童成彪，方 鑫

水工試驗

固定錐形閥消能設施消能效果的數值模擬研究

蘇克巴圖1，童成彪2，方 鑫2

（1.新疆巴州若羌河米蘭河流域管理處，新疆巴州841800；2.中閥科技（長沙）閥門有限公司，長沙410007）

針對固定錐形閥的閥后出口水流流速較大的問題，需要在閥后布置相應消能設施來消除多余動能，通過使用VOF方法對錐形閥排出流體的流動狀態進行計算模擬，研究和探討了不同消能設施布置方式對出口水流能量消除的影響。結果表明，合理的錐形閥后消能設施布置能夠有效消除閥門出口動能，最大消能率達89.6%。消能效率與消能池深度和池長均同時存在關系，較深且較長的消能池和較淺且較短的消能池布置方案具有較好消能效果。

固定錐形閥；VOF方法；消能；數值模擬

1 引言

固定錐形閥主要用于水利工程大壩放空、水電站機組旁路、水利或水電灌溉系統的流量調節和能量消除［1-2］。該閥門出口水流具有較高流速，一般情況下，水流直接對空排放，通過水與空氣之間的摻氣作用將動能消除。但實際應用中由于受到場地空間限制，通常不允許錐形閥出口有大范圍噴射水流。

針對錐形閥半淹沒出流工況，上游水流經過錐形閥的作用將靜壓能轉化為動壓能，并沖擊下游的消能池等設施，當水流由急流到緩流過程中將會發生水躍現象［3］，而水躍具有消能特性，閥后消能池的設計主要原理就是利用可控制水躍來進行消能。

由于錐形閥出口水流流速較高，其在下游消能池中進行消能時，水流流態混亂，三維紊流劇烈，通過經驗計算公式難以準確描述其消能效果，而物理模型試驗周期長、投資大，隨著計算機數值計算技術發展，水流流動模擬計算應用越來越廣泛，同時具有較高準確度。數值模擬已經能夠比較真實地反映水流運動特性，從而為工程方案優化節省時間，提高研究效率。

2 數學模型

2.1 自由液面的數值模擬方法

利用有限體積法對通過錐形閥的水流在下游消能池中的流動狀態進行模擬分析［4］，進而研究水流流動特點和消能池的消能效果，為設計合理的消能設施提供參考。水流在消能池中的運動屬于明渠流范疇，在進行數值模擬計算過程中將使用到VOF（Volume of fluid）方法［5］來進行水流與空氣之間的交界面跟蹤計算。

VOF方法是由Hirt和Nichols在1981年提出的處理復雜自由表面的有效方法，是目前應用非常廣泛的一種追蹤自由表面的數值方法。該方法使用靜態或以某種確定形狀網格以適應與界面形狀的演化。在進行流體力學的數值計算中通過定義流體體積函數VF=F（x，y，z，t）表示計算區域內流體體積占據計算區域的相對比例，對于某個單元，VF=1表示該單元被流體完全充滿；VF=0表示該單元是個空單元，沒有流體；VF=0~1表示該單元被流體部分充滿，VOF法只用一個函數就可描述自由表面的各種復雜變化。

基于VOF方法連續性方程和動量守恒方程描述為式（1）、式（2）。

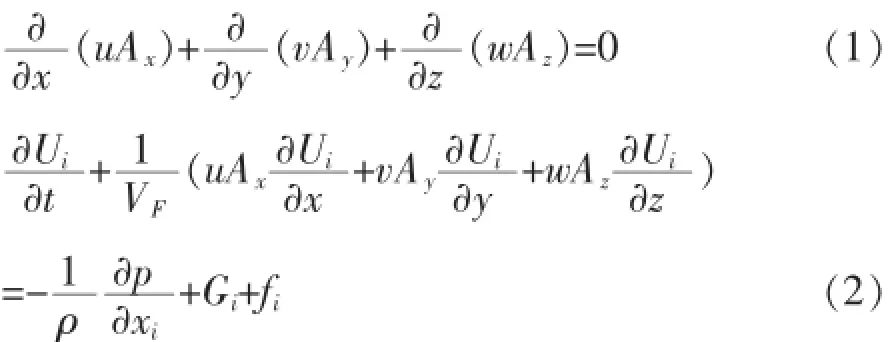
式中u，v，w為x，y，z方向上的速度；Ax，Ay，Az為單元內x，y，z方向上可流動的面積分數；Ui為i方向上的速度，i為x，y，z 3個方向；VF為單元內流體體積分數；ρ為流體密度；xi為i方向坐標，i為x，y，z3個方向；p為流體壓力；Gi為x，y，z方向上的重力加速度；fi為x，y，z方向上的黏滯力。

2.2 RNG k-ε湍流模型

在流體數值模擬計算中，若流動狀態為湍流，則直接求解N-S方程將消耗巨大的計算機資源和時間，故實際工程中湍流問題處理主要是對瞬態N-S方程進行時間平均處理，同時補充反映湍流特性的其他方程使控制方程組封閉，進而使方程存在唯一解。

對于湍流流動數值方法，工程上通常采用標準k-epsilon兩方程模型［6］進行求解計算，而對于具有強旋流的高雷諾數問題，RNG k-epsilon模型［7］則具有更準確的描述，其湍動能方程和湍動能耗散率方程為式（3）、式（4）。

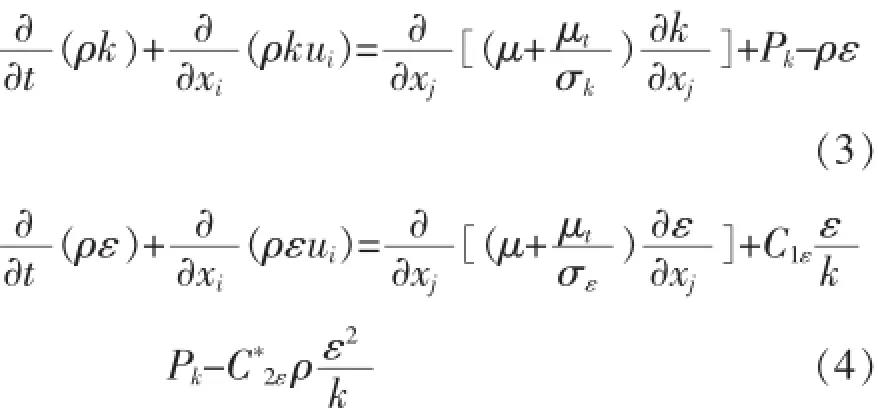
式中ρ為密度；k為紊流動能；ε為紊流動能耗散率；ui為速度；μ為黏度；μt為紊流粘度；σk為k值的紊流普朗特數；σε為ε值的紊流普朗特數；Pk為由于平均速度梯度產生的紊流動能；C1ε為常數1.42；C*2ε為常數1.68。

3 錐形閥后消能設施數值計算

在錐形閥后的消能池中，水躍現象將泄水建筑物泄出的急流轉變為緩流以絕大部分消除動能，進而防止高速水流沖刷下游水工建筑物。水躍消能主要靠水躍產生的表面旋滾及旋滾與底流間的強烈紊動﹑剪切和摻混作用。由于水躍流態復雜，水流波動劇烈，應用數值模擬方法對其進行研究得到越來越廣泛的應用。一般情況下錐形閥后空間較小，且附近存在多種水工建筑物，在設計下游消能設施時，宜選用消能池加消能坎的綜合消能形式。針對此綜合式消能池設計，主要考慮參數為消能坎高c、消能池深S和消能池長度Lk等。

數值計算區域主要包括錐形閥上游入口管道，固定錐形閥及閥下游消能設施，計算模型設計如圖2。模擬計算過程中設置上游入口總水頭為50m，下游出口為自由出流，壓力大小為大氣壓，管道和消能池壁設為無滑移的壁面邊界條件，而固定錐形閥的通徑則設置為2000mm。

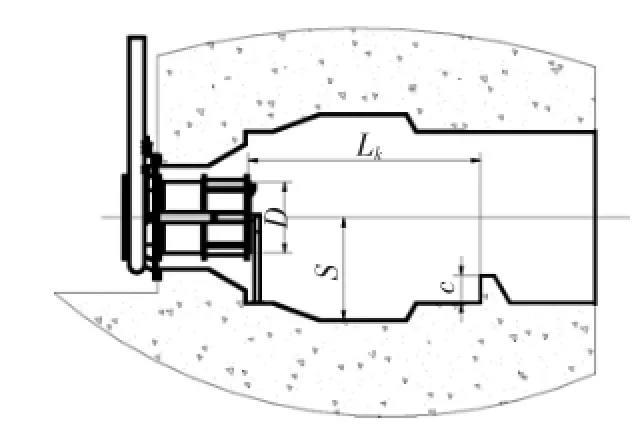
圖1錐形閥消能設施設計

圖2 和圖3中為計算區域內壓力分布云圖和速度分布云圖，表明壓力和速度在固定錐形閥前和閥后變化較大，在錐形閥后壓力出現較大程度降低，且閥出口位置速度最大。由此可知，上游水流經過錐形閥作用之后，將其壓力能轉換為動能并進入消能池中，由于速度劇烈變化導致消能池中水流波動劇烈而產生水躍現象，在此過程中絕大部分能量被消除，故在下游出口位置的速度和壓力降到最低，達到消能的效果。

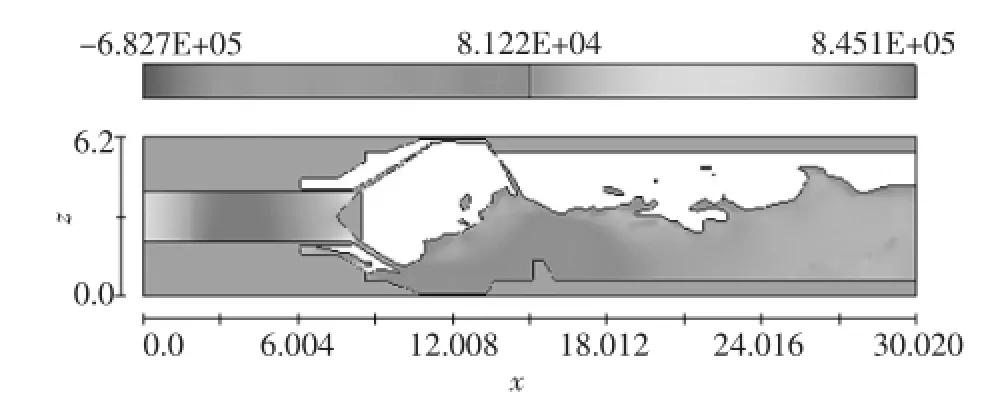
圖2 壓力分布云圖

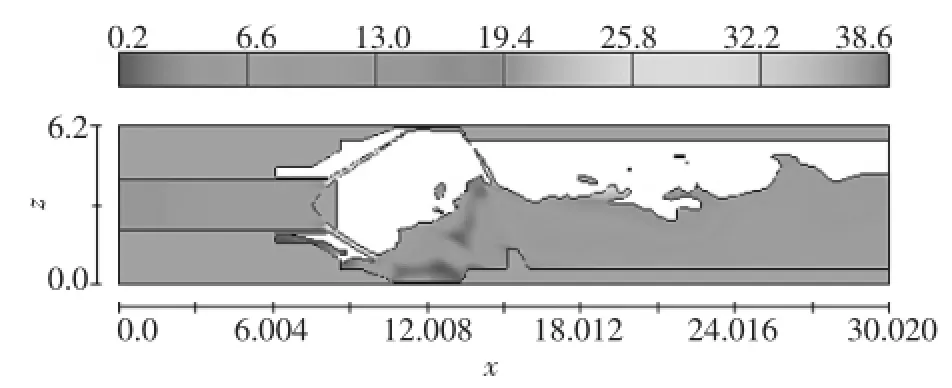
圖3 速度分布云圖

計算區域內的流體湍動能分布情況如圖4。由湍動能分布特點可知，在消能池內和消能池出口位置的水流湍動能較大，表明這些位置湍流較為劇烈，能量消除主要在該處進行。

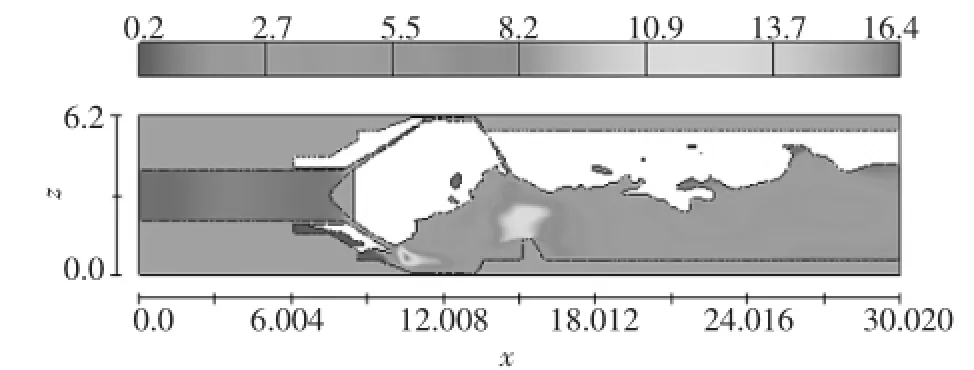
圖4 湍動能分布

根據數值模擬結果得到水流在沿流動方向上速度變化特點如圖5，可以發現，水流在上游具有較高速度和水頭，然后在通過固定錐形閥時由于導流錐作用使流體壓力能轉化為動能，故其速度瞬間增大并流入下游消能池中，由于消能池作用而使其速度又瞬間降低并產生水躍，水躍產生表面旋滾及旋滾與底流間的強烈紊動﹑剪切和摻混作用使水流絕大部分能量被消除掉，水躍之后其速度有一定回升，在整個過程中能量被消除而出流速度較小，不會對下游水工建筑物造成沖刷。

圖5 沿流動方向的速度變化情況

在進行數值計算的過程中，主要考慮消能池總深度和長度對錐形閥后出口水流消能效果的影響，故在相同上游水頭條件下，設置不同消能設施布置方案，進而考察和比較其消能情況。

根據水力學理論，流體能量主要分為兩部分，靜止流體所具有的靜壓能及流體分子運動過程中的動壓能。所以在分析消能池的消能特點時，采用比較上游和消能池出口的總壓降低的程度，從而比較不同結構消能設施的消能效果。計算區域內流體介質能量計算按照式（5）進行［8］。

式中P為流體具有的靜壓值；ρ為流體具有的密度；g為重力加速度；v為選取截面的平均流速。

為了比較消能效果的優異程度，引入消能效率概念，從而利用比較消能效率的大小來評價不同消能設施所產生的消能效果，計算方法如式（6）。

式中K為消能效率；Ein為閥前水流具有的能量；Eout為閥后水流具有的能量。

通過CFD計算分析，在獲得計算區域內流體流動分布情況基礎上，利用式（5）和式（6）對數值模擬結果進行處理得到消能效率，不同的消能設施布置方案和消能率的大小如表1。D為圖1中錐形閥公稱直徑。

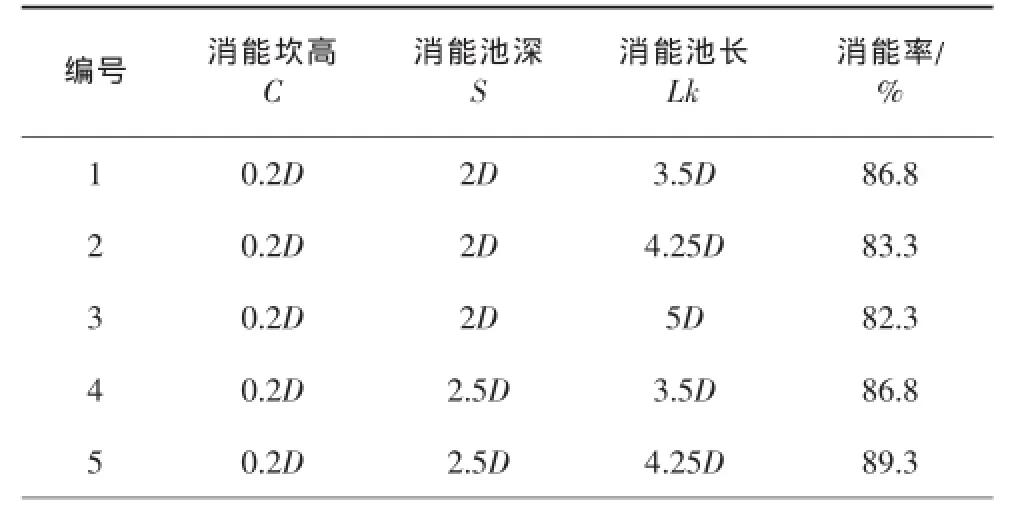
表1 消能設施布置及消能率

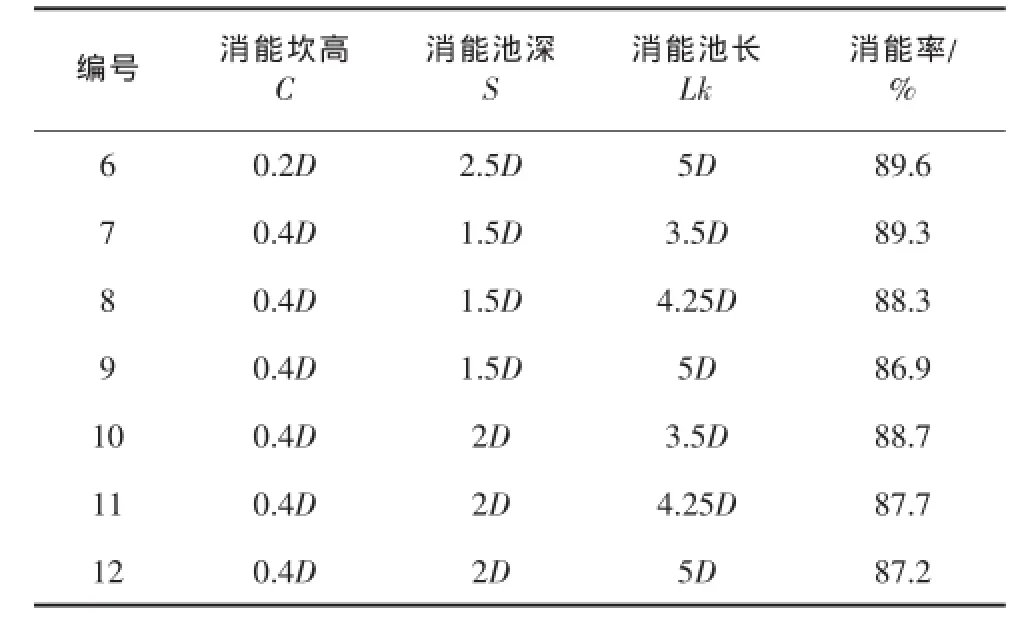
續表1

數值模擬結果表明，錐形閥后的消能設施能夠有效消除閥門出口動能，消能率最大可達89.6%。在池深較淺時候，消能池對水流消能率隨池長的增加而降低；而在池較深時則情況相反。消能池的消能效率與深度和池長均同時存在關系，較深且較長消能池和較淺且較短消能池布置方案具有較好的消能效果，如考慮建造成本則優先使用較深且較淺消能池布置方案。

為了研究不同流動邊界下相同的消能設施設置的消能效果變化情況，以下使用編號6的消能池設計方案進行計算分析。系數描述如式（7）［9］：

式中v為錐形閥出口水流速度；g為重力加速度；h為下游消能池水深。

在進行數值模擬過程中，錐形閥上游設置不同總水頭大小，進而改變了進入消能池水流流速，其弗勞德數亦變化，比較其消能效率的變化情況，根據模擬結果得到弗勞德數與消能效率的關系，如圖6。

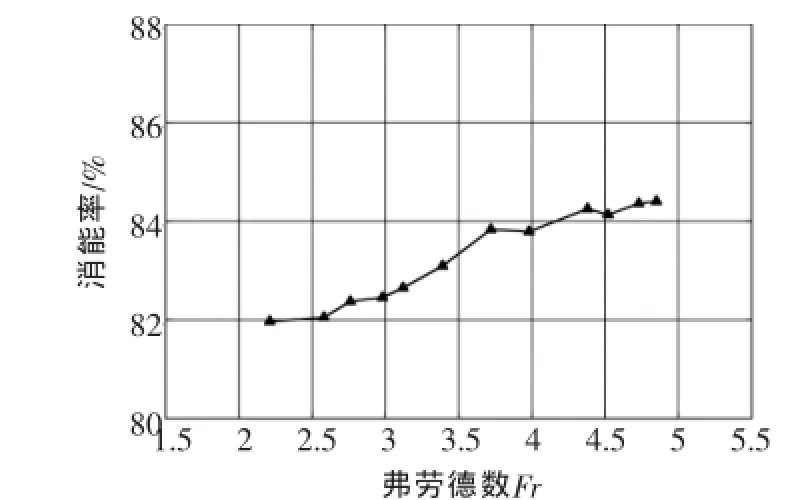
圖6 不同弗勞德數下的消能效率情況

由圖6可知，設置消能池后能夠有效消除錐形閥出口水流動能，流動狀態越湍急，弗勞德數越高，則消能效率越高；消能率隨著弗勞德數的減小而有所降低，但在一定的弗勞德數范圍內，合理設置下游消能池的尺寸方案布置能夠消除絕大部分水流動能，從消能池出來的水流具有較低能量，速度較低，不會對下游水工建筑物造成沖刷等影響。

4 結語

（1）運用CFD技術對錐形閥出口水流的流態情況進行數值模擬，通過計算能夠較好確定各主要尺寸值，優化了消能設施的布置和設計。

（2）依靠VOF方法在數值計算過程中進行表面定位、跟蹤及演化，能夠精確計算出流體表面變化和分布情況，是目前應用最為廣泛的自由液面數值處理方法。而RNG k-epsilon湍流模型則能夠更好地處理具有強旋流的高雷諾數流動問題。

（3）通過CFD計算分析，消能率將高達87%，消能池的消能效率與消能池的深度和池長均同時存在關系。消能池的消能效率隨著弗勞德數的增大而升高。數值模擬結果能夠為合理布置和設計閥后消能設施提供有力參考。

［1］M.C.約翰遜，劉洪波.錐形固定閥消能［J］.水利水電快報，2001，22（24）:7-8.

［2］李翠艷，張宗孝，鄧瑩瑩.錐形閥消力池優化試驗研究［J］.電網與水力發電進展，2008，24（3）:54-56.

［3］李煒.水力計算手冊［K］.北京:中國水利水電出版社，2006．

［4］張永學，李振林.流體機械內部流動數值模擬方法綜述［J］.流體機械，2006，34（7）:34-38.

［5］Hirt，C.W.；Nichols，B.D."Volume of fluid（VOF）method for the dynamics of free boundaries"，Journal of Computational Physics.1981，39（1）：201-225.

［6］B.E.Launder，D.B.Spalding.Lectures in Mathematical Models of Turbulence.Academic Press，London，1972.

［7］V Yakhot，SA Orszag.Renormalization-group analysis of turbulence.Physical review letters.1986，57（14）：1722-1724.

［8］D Stephens，MC Johnson，ZB Sharp.Design Considerations for Fixed-Cone Valve with Baffled Hood.Journal of Hydraulic Engineering，2011，138（2）:204-209.

［9］Newman JN.Marine hydrodynamics［M］.The MIT Press，1977.

Numerical Simulation of the Energy Dissipation Device of Fixed-Cone Valve

SU ke ba tu，TONG Cheng-biao，FANG Xin
（1.Bazhou Milan Ruogiang River Basin Management Office,Bazhou 841800,China；2.China Valve Technology（Changsha）Co.，Ltd.，Changsha 410007，China）

Since the outlet of fixed-cone valve has a high velocity，some energy dissipation device after the valves must be laid out to eliminate the extra kinetic energy，The flow condition of fluid discharged from the fixed-cone valve would be simulated with the VOF method in the paper，and the influence of different energy dissipation device layout plans were studied and discussed.The results of numerical simulation showed that，Reasonable energy dissipation device behind the fixed-cone valve can effectively eliminate the kinetic energy after the outlet of the valve，the dissipation ratio can reach as high as 89.6%.Both the depth and length of the energy dissipation pool have relationship with the efficiency of energy dissipation，a deeper and longer pool or a shallower and shorter pool can get a better energy dissipation result.

Fixed-cone valve；VOF method；Energy dissipation；Numerical simulation

TV653

A

1672-9900（2016）04-0070-04

2016-06-08

蘇克巴圖（1972-），男（蒙古族），新疆和靜人，工程師，主要從事水利工程設計、施工工作，（Tel）18009965322。