基于高斯采樣和隨機采樣聚類的差分演化算法

程　鋼， 劉　罡， 胡延忠

(湖北工業大學計算機學院， 湖北 武漢 430068)

基于高斯采樣和隨機采樣聚類的差分演化算法

程鋼， 劉罡， 胡延忠

(湖北工業大學計算機學院， 湖北 武漢 430068)

[摘要]基于中心采樣的概念，提出隨機采樣方法。研究差分演化算法，提出基于高斯采樣和隨機采樣的聚類差分演化算法。通過實驗，論證了高斯采樣和隨機采樣顯著的加快收斂速度、提升算法的求解能力，表明該算法對復雜的全局優化問題有很好地求解能力，比經典差分演化算法具有更好的求解性能。

[關鍵詞]差分演化算法； 全局優化； 隨機采樣

針對全局優化問題， R.storn和K.Price提出差分演化算法(Differential Evolution，DE)，算法采用實數編碼方式，其原理及演化流程與遺傳算法十分相似，如父代生成子代的操作均包括變異、交叉和選擇，且很好的解決了全局優化問題[1-4]。

本文提出隨機采樣的方法。隨機采樣與中心采樣相比，前者因其隨機性，其搜索能力更靈活、更有效。由于差分演化算法擅長全局搜索整個解空間，解的局部區域開拓相對緩慢。為了改進差分演化算法的求解性能，本文將隨機采樣、高斯采樣和一步K均值聚類方法結合到差分演化算法中，旨在提高差分演化算法對解得局部區域的開拓能力，提出了基于高斯采樣和隨機采樣的聚類差分演化算法(GRCDE)。

1差分演化算法

差分演化算法利用差分變異操作將種群中任意個體選取兩個差分向量加權；再根據一定規則加到新的個體上，隨后進入交叉操作，通過交叉系數產生新個體，該變異方式有效利用種群分布特性，提高了全局搜索能力，避免了其它演化算法中存在的變異機制不足現象；算法在選擇操作上采取貪婪選擇操作，選擇適應值大的個體保存到下一代。

差分演化算法的關鍵步驟：

1)變異操作

變異操作指算法將種群中任意個體選取兩個差分向量加權從上一代種群中生成新個體進入下一代。變異機制實現了對搜索空間的搜索。

在差分演化算法中，很多變異操作機制在文獻[5]提出，現將一些比較知名的變異機制介紹如下：

隨機差分向量法

DE/rand/1 :Vi=Xr1+F(Xr2-Xr3)

(1)

最優解加隨機向量差分法

DE/best/1:Vi=Xbest+F(Xr1-Xr2)

(2)

最優解與隨機向量差分法

DE/rand-to-best/1:

Vi=Xi+λ(Xbest-Xi)+F(Xr1-Xr2)

(3)

其中，Vi是目標向量，Xi是變異向量。r1，r2，r3∈{1，2,…,NP}是隨機選擇不同的整數且不同于運行指數i；Xbest代表目前這一代最好的個體；F(>0)變異因子；λ是增加的控制參數。

2)交叉操作

交叉操作的目的是對種群中前幾代所求得的解進行重組。交叉操作對種群中的當前向量和變異向量進行重組，從而構建了新的試驗向量；再經過交叉操作，通過對上一代向量和新的試驗向量的適應值進行比較，兩者中適應值高的進入下一代。交叉操作如下：

其中uij是試驗向量。

3)選擇操作

選擇操作采用“貪婪”的搜索策略，經過前面兩步操作后，生成的試驗向量個體ui,G與目標向量個體Vi,G進行競爭，對兩者中適應值相比較，更優的個體才被選中進入下一代。選擇操作如

其中Xi,G+1是新的種群個體向量。

2改進的差分演化算法

2.1隨機采樣

中心采樣是由Rahnamayan[6]提出。在搜索空間中，搜索區間的中心有很大概率接近問題的解。隨機采樣基于中心采樣的概念，給定搜索區間[-(|a|+|b|),(|a|+|b|)],如圖1所示，該區間內的隨機點按式(4)所示，對于n維情況，具體如

ri=(|ai|+|bi|) rand(-1,1)

(4)

由于最優解的位置具有不確定性，為了增加包含最優解的概率，需要對搜索區間進行擴展。由于ri位于區間[-(|a|+|b|),(|a|+|b|)]內的隨機性，使其在整個區間內移動。在中心采樣中，ci是位于區間(ai，bi)的固定中心點。與中心采樣相比，隨機采樣的搜索區間更大。事實上，中心采樣可以被視為隨機采樣的子集。當rand(-1, 1)為0.5時，隨機采樣退化為中心采樣。與中心采樣使用的固定值相比，隨機采樣使用的隨機數有更大的靈活性，使得候選解有更大的機會接近全局最優解。直觀的解釋如圖1所示。

圖 1　隨機抽樣圖

圖中x是候選解，s是全局最優解，r是搜索區間 [-(|a|+|b|),(|a|+|b|)]內產生的隨機點，r=(|a|+|b|)rand(-1,1)(其中rand(-1,1)是均勻分布在(-1,1)的隨機數)。

整個搜索區間[-(|a|+|b|),(|a|+|b|)]可以分為[-(|a|+|b|),r]和[r,(|a|+|b|)]兩個子區間。由此可見，x和s既可能在不同子區間，也可能在同一子區間。當x和s在不同子區間時，r位于x和s之間。無論s在何位置，x和r分別到s的距離都滿足‖x-s‖≥‖r-s‖。當x和s在相同的子區間時，則存在x和r一起競爭誰更接近s。由于s位置的不確定性，隨機點r可能比區間[-(|a|+|b|),(|a|+|b|)]的中心點更接近全局最優解s。因此，隨機采樣具有更大靈活性，使得隨機點r有更高的概率接近全局最優解s。

2.2隨機采樣的變異機制和高斯采樣的變異機制

在演化階段初期，由于種群具有較大的分布偏差，搜索過程主要集中于對整個空間的全局搜索；隨著運行代數增長，分布偏差逐漸變小，搜索過程就逐步轉為對局部區域的開拓。當搜索過程處于局部開拓時，使用隨機采樣變異機制和高斯采樣變異機制對每個子種群進行搜索。隨機采樣和高斯采樣都具備很好的局部開拓的性能。數學上表示為：

隨機變異機制

(5)

高斯變異機制

(6)

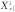
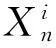
2.3基于高斯采樣和隨機采樣聚類的差分演化算法

差分演化算法擅長全局搜索整個解空間，然而差分演化算法對解的局部區域開拓相對緩慢。為此本文將隨機采樣、高斯采樣和一步K均值聚類方法結合到差分演化算法中，試圖提高差分演化算法對局部區域的開拓能力；提出了基于高斯采樣和隨機采樣的聚類差分演化算法(GRCDE)。在GRCDE中，使用目標空間距離測度的一步K均值聚類算法用于劃分種群。利用高斯變異機制和隨機變異機制分別在每個子種群中搜索新的個體。基于兩種不同原理的變異機制可以有效地對子空間進行搜索，增強差分演化算法對局部區域的開拓能力。在GRCDE中，2種變異機制生成了兩個新的試驗向量，然后兩個試驗向量中最好的一個向量被用來替換子種群中的目標向量。GRCDE使用的差分演化算法變異機制采用折衷選擇機制[5,7]。

具體情況如式(7)所示

Vi= Xr1+ F (Xr2- Xr3)

(7)

其中，Xr1的適應值優于Xi的適應值，r1≠r2≠r3≠i。這種算法變異機制是從當前種群中按如下要求隨機選擇一個個體，該個體的適應值必須優于作為變異對象的目標個體適應值。這種方法在保持收斂速率的同時，有助于維持種群的多樣性。

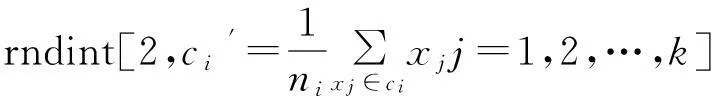
算法1：GRCDE算法

Step1：隨機生成初始種群P，在種群P中對每一個個體的適應值進行評估，設置迭代計數器t=1；

Step2：當終止標準不滿足繼續執行；

Step3：根據Vi= Xr1+ F (Xr2- Xr3) 生成新的試驗向量V={vi,1;vi,2,…,vi,D}；

Step4：依據t%m=0判斷多少代進行一次聚類；

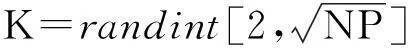
Step 6：(隨機變異機制和高斯變異機制)對于第i個子種群，使用隨機變異機制生成的新的個體A，同時也使用高斯變異機制生成新的個體B。在A和B通過競爭后，選取優勝者去取代第i個子種群中相應的個體。

Step 7：判斷是否達到終止輸出條件，滿足輸出結果，否則繼續Step2。

在GRCDE中，種群被分成K個子種群，并且利用兩種不同的變異操作機制對子種群進行開拓。多個不同的變異機制與單個的變異機制相比，可以同時搜索更多的個體。通過多個父體交叉后產生的新個體之間進行競爭比較，優勝者將被選出并進入下一代種群。這種方法提高了搜索效率并且增加了搜索到最優解的機會。

3GRCDE性能分析

3.1實驗設置

針對GRCDE的性能，選取了3個演化學界常用基礎函數進行測試。3個函數都是高維函數，f1是單峰函數，f2是有噪聲的四次函數，f3是有很多局部最小值的多峰函數。

實驗設置如下：維度D=30；種群規模NP=100；變異因子F=0.5；交叉概率因子CR=0.9；聚類周期m=MAX_NFEs(最大個體評估次數)=5000；運行次數：各種算法將每個函數運行50次。“Mean”表示在50次運行內發現了最好的適應值。“SR”表示成功運行的次數。“NFEs”是評估適應值的數量。 “MeanNFEs”表示算法的函數評估數量的平均數量成功。“Stddev”表示函數標準偏差值和最大評估適應性數量平均值。如果算法在運行50次沒有1次成功，表示算法對該問題不適用，并用“N/A”表示。

(xi-1)2), -30≤xi≤30

(8)

-1.28≤xi≤1.28

(9)

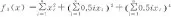
-5≤xi≤10

(10)

3.2對GRCDE和DE的比較

1)比較解的精度

對于DE/rand/1,DE/best/1/和GRCDE的基礎測試函數，最大評估次數MAX_NFEs=2.00E+05，并在表1中進行了總結。在圖2中DE/rand/1，DE/best/1，GRCDE分別運行函數f1,f2,f3的演化過程，關于DE/rand/1,DE/best/1和GRCDE性能如圖2所示。通過分析表1和圖2的結果可知，在上述實驗中GRCDE求解性能比DE優越。

(a)函數f1

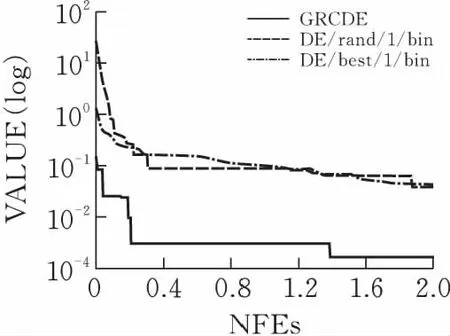
(b)函數f2

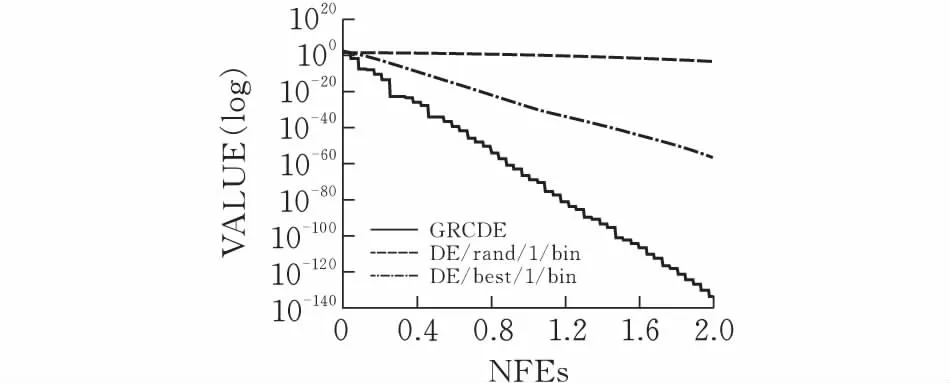
(c)函數f3圖 2　算法運行幾種測試函數的過程

2)比較收斂速度和成功運行的次數

由于收斂速度是算法性能一項重要指標，現比較了不同算法的收斂速度。需要對目標函數的閾值進行選擇和比較，對于所有函數不同的閾值具有不同功能，表2中Threshold表示目標函數的閾值，其中f1、f3閾值設為1.00×10-10,f2閾值設為5.00×10-3。在到達終止標準時算法終止，在本節中，當最好的適應值低于預定義的閾值，或者個體評估次數的數量(NFEs)達到最大評估次數 (MAX_NFEs= 5.00×105)時，算法終止運算。

表1　所有函數最好適應值的平均值和協方差的結果

表2　在預設精度下評估次數的平均值和成功運行次數

表2中所有函數都進行50次獨立的運算，然后記錄收斂到閾值需要的平均個體評估次數的值和SR，其中SR是成功運行的次數。3種算法的NFEs平均值、標準偏差和成功運行次數SR，如表2所示。在表2中，所有算法的最大評估次數(MAX_NFEs)均為500,000，“N/A”代表到最大評估次數 (MAX_NFEs) 時精度水平沒有達到要求。由此可見，GRCDE在3個函數中的收斂速度要比DE/best/1和DE/rand/1快，同時與差分演化算法相比，在GRCDE中NFEs的數量明顯減少。

4結束語

在GRCDE中，利用高斯采樣和隨機采樣設計兩種不同的變異機制。不同的變異機制充分利用不同的搜索技術以不同的搜索方式對解空間進行搜索，這樣就提高了全局搜索的效率和局部開拓的能力。值得注意的是，如果種群的規模太小，變異機制的作用會受到限制。在GRCDE中，當子種群的規模大于5時，變異機制才被用來搜索這個子種群。

實驗結果表明，高斯采樣和隨機采樣會顯著加快收斂速度，提升差分演化算法的求解能力。本文提出GRCDE在對復雜的全局優化中具備很好地求解能力，這種改進的差分演化算法具有良好求解性能。

[參考文獻]

[1]ReddyAS,VaisakhK.Shuffleddifferentialevolutionforlargescaleeconomicdispatch[J].ElectricPowerSystemsResearch, 2013, 96: 237-245.

[2]ZhongY,ZhangL.Remotesensingimagesubpixelmappingbasedonadaptivedifferentialevolution[J].Systems,Man,andCybernetics,PartB:Cybernetics,IEEETransactionson, 2012, 42(5): 1306-1329.

[3]ChakrabortyUK,AbbottTE,DasSK.PEMfuelcellmodelingusingdifferentialevolution[J].Energy, 2012, 40(1): 387-399.

[4]KhushabaRN,Al-AniA,Al-JumailyA.Featuresubsetselectionusingdifferentialevolutionandastatisticalrepairmechanism[J].ExpertSystemswithApplications, 2011, 38(9): 11 515-11 526.

[5]PriceKV.Differentialevolutionvs.thefunctionsofthe2ndICEO[C]//EvolutionaryComputation, 1997.IEEEInternationalConferenceon.IEEE, 1997: 153-157.

[6]RahnamayanS,WangGG.Center-basedsamplingforpopulation-basedalgorithms[C]//EvolutionaryComputation, 2009.CEC’09.IEEECongresson.IEEE, 2009: 933-938.

[7]PriceK,StornR,LampinenJ.differentialevolution-apracticalapproachtoglobaloptimization[M].BerlinGermany：Springer, 2005.

[責任編校： 張巖芳]

A Clustering Differential Evolution Algorithm Based on Random Sampling and Gaussian Sampling

CHENG Gang， LIU Gang， HU Yanzhong

(SchoolofComputerScience,HubeiUniv.ofTech. ,Wuhan430068,China)

Abstract：Based on the concept of center-based sampling, the paper proposed a method of random sampling. It studied the Differential Evolution, proposing the clustering differential evolution algorithm based on random sampling and Gaussian sampling (GRCDE). Experiment results indicate the Gaussian sampling and the random sampling remarkably accelerate the convergence rate and improves exploitation ability of DE. It shows that GRCDE has a better solving ability and our proposed GRCDE performs better than some DE variants.

Keywords：Differential Evolution, global optimization, random sampling

[收稿日期]2015-05-18

[基金項目]國家自然科學基金項目(61300127)

[作者簡介]程鋼(1983-)， 男， 湖北洪湖人，湖北工業大學碩士研究生，研究方向為差分演化算法，圖論

[文章編號]1003-4684(2016)02-0045-03

[中圖分類號]TP301.6

[文獻標識碼]：A