社會調查數據建模及基于超圖的數據分析方法

奚曉曄　嚴利民　殷曉文

摘 要：針對現今的社會調查數據處理與分析中存在的問題，該文通過三維矩陣建立了社會調查數據的數學模型。將每一題表示為空間中的一個維度，每一張問卷表示成一個矩陣，將多個矩陣疊加即可得到社會調查數據的三維矩陣模型。在建立三維矩陣模型的基礎上，可以利用三維矩陣的性質對其進行多種數學處理，也可以采用超圖理論對數據進行進一步的分析，大大豐富了調查數據的處理方法。

關鍵詞：社會調查數據 三維矩陣 超圖

中圖分類號：P208 文獻標識碼：A 文章編號：1672-3791（2016）02（a）-0003-04

Abstract：In view of the problems of the social survey data processing and analysis， this paper establishes the mathematical model of three dimensional matrix which is based on the three dimensional matrix.On the basis of the established three dimensional matrix model，we can use the properties of three dimensional matrix to deal it with a variety of mathematical methods， and use the hypergraph theory for further analysis. This enriches the method of the survey data processing greatly.

Key Words：Social survey data；Three-dimension matrix；Hypergraph

社會調查是了解各方面信息的重要途徑之一，社會調查數據主要是通過調查問卷的方法得到的。由于社會調查數據的維數較高，加上人為主觀因素，數據類型主要為二元變量、離散變量、序數變量等為主，所以對于社會調查數據的分析和處理大都基于統計學，只對單一題目進行統計學分析，其分析方法主要是基于題型進行處理的，對于題目和題目之間的關系很少關心[1]。許多數據挖掘算法因為種種限制無法在社會調查的數據分析中得到應用。因為方法的限制，所以現在很多社會調查只能驗證事先想好的內容和假設，很少可以對高維數據進行相對復雜的回歸分析處理。

根據以上存在的問題，該文建立了基于三維矩陣的數學模型，將單選題、多選題和排序題用向量形式進行表示，每一題定義為空間中的一個維度，從而所有的題目就可以構成一個N維空間。每份問卷的信息用一個M×N矩陣表示。這樣表示可以將所有問卷內容當作一個整體，作為后續算法的基礎。

1 社會調查數據的特點

通常情況下，社會調查數據特點如下。

（1）相關性。對于一個樣本個體而言，它具有本身的多個特征，這些特征之間就具有一定的相關性。對于多個樣本而言，個體與個體的特征之間具有相關性。如果樣本隨時間而變化，那么該樣本在不同時刻的特征之間又具有相關性。因此，由于上述多個原因使得社會調查數據具有了復雜的相關性，傳統的統計學調查難以解決這樣的問題。

（2）離散性。因為社會調查數據是通過自填式問卷、網絡調查數據庫等方法得到，所以社會調查數據一般以離散變量為主，且這些數據之間只有標示作用，并沒有嚴格的邏輯關系。

（3）模糊性。社會調查數據當中不可避免的會接觸到各種表達方式和概念，因此，它具有模糊性。

因為由自填式問卷或結構式訪問的方法得到的社會調查數據具有以上特點，所以在實際應用中基于統計學的處理方法只能籠統的顯示數據的部分特性，如頻數、離散程度等[2]。對于數據之間的關系只能分析出維數極少的大致的關系。

而且利用軟件進行數據挖掘時，因為現有的軟件中的數據挖掘算法對于數據類型和格式要求較高，所以能應用到的數據挖掘算法很少。就算是數據要求較低的關聯分析，其結果也存在大量的冗余。因此，我們需要建立一個合適的社會調查數據的數學模型來完善原先的方法并使跟多的數據挖掘方法可以運用到其中，使得結果更準確。

2 社會調查數據的建模

研究中我們發現，三維矩陣可適用于社會調查數據的建模。

2.1 三維矩陣的定義

三維矩陣的定義：由n個p×q階的矩陣組成的n×p×q階的矩陣A稱為三維矩陣，又稱立體陣。Ak，i，j表示三維矩陣A的第k層，第i行，第j列上的元素。其中n，p，q分別表示三維矩陣的高度，厚度和寬度。

2.2 三維矩陣模型的建立

調查問卷的題目一般有三種類型：單選題、多選題和排序題。這三類題目都可以表示成向量的形式，其中每一道單選題、多選題可以表示成一個向量，排序題可以表示成多個向量組成的矩陣。對于單選題和多選題，可以按選項的順序可以表示成一個向量，其中選中的項用“1”表示，未選中的項用“0”表示。對于排序題，可以表示成一個n×n的方陣，其中n表示該排序題的選項個數，。這樣，每一題就可以定義為空間中的一個維度，從而所有的題目就可以構成一個N維空間。每份調查問卷的信息用一個M×N矩陣表示（M為題目的最大選項數），其在每一維上的選擇稱之為一個元素，這樣每份問卷的信息就包括了N個元素。以第1，2，3題數據為例，其中第1題為單選題選擇“B”，用向量表示為一個元素，第2題為多選題選擇“ACE”，用向量表示為一個元素，第3題為排序題順序為CBADEFIHG，用矩陣表示，每一個列向量是一個元素，如圖1所示。

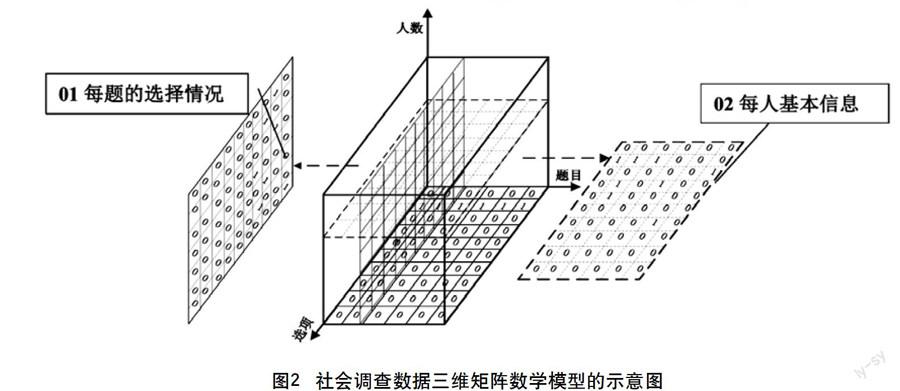
那么，假設有一問卷信息用一個大小為M×N的矩陣表示。K份的問卷信息就可以用K個大小為M×N的矩陣表示。將這K個矩陣疊加，形成一個三維矩陣。這個三維矩陣就是我們建立的三維矩陣數學模型，如圖2所示。

在圖2中我們看到，該三維矩陣數學模型有三個坐標軸，它們分別是題目，人數，選項。題目軸以每一道題為一個單位；人數軸以每一份問卷為一個單位；選項軸的刻度為A，B，C，D，E，F等題目選項，其個數為該調查問卷中選項最多的題目的選項個數。

在此基礎之上，這樣的三維矩陣具有以下性質。

（1）在題目軸中選取對應的題目，將三維矩陣面向豎切得到截面1（如圖2中01所示），截面2表示每一道題所有人選擇的信息。

（2）在人數軸中選取對應的人，將三維矩陣橫切得到橫截面1（如圖2中02所示），橫截面1表示對應的人選擇所有題目的信息。

在得到三維矩陣后，可對它進行像素化處理，置1的元素用黑點代替，置0元素的則空白，在得到像素化三維矩陣后我們可以將三維矩陣沿著人數維度上向下投影，這樣就可以得到一個具有濃黑不一的點的平面。通過這些點的濃度，可以知道每一選項選擇的人數。接下來我們可用灰度級表示點的濃度，篩選出濃度大于一定程度的點，在此基礎上進行后續算法處理。

上述三維矩陣數學模型具有數學三維矩陣的所有性質，可依據調查問卷的需求進行轉置，加權、相乘、篩選等數學處理，另外在數學處理的基礎上，采用超圖理論可以大大豐富了調查問卷的處理方法。

3 基于超圖算法的調查問卷分析技術

超圖是離散數學中重要的內容，是對圖論的推廣[3]。超圖是有限集合的子系統，它是一個由頂點的集合V和超邊集合E組成的二元對，超圖的一條邊可以有多個頂點的特性，這與一般的圖有很大不同。超圖分為有向超圖與無向超圖兩類，在無向超圖的每條超邊上添加方向后得到的有向二元對就是有向超圖。超圖在許多領域有廣泛的應用。

大家可以利用無向超圖表示每一道題的選擇情況，先將這每一題的每一個選項設成一個節點，然后將三維矩陣從上向下投影，如果某一題的若干個選項同時被一個人選擇，就用一條超邊包圍這些節點，那么選這些選項的人越多，投影得到的超邊就越濃。這樣就用超圖表示了問卷中每道題的信息，可以進行聚類處理。

利用有向超圖，可以將關聯規則表示成有向超圖的形式，在得到了關聯規則后，設實際中得到的關聯規則的形式為：，前項和后項都是由多個項組成的集合。該文定義一條關聯規則由一條有向超邊表示，有向超邊的頭節點表示關聯規則的前項，有向超邊的尾節點表示關聯規則的后項。每條有向超邊的頭節點和尾節點均可以為多個，如此便成功表示了復合規則，從而可以使用相關算法進行冗余規則檢測。

通過基于有向超圖的冗余規則檢測就可以將關聯規則之間存在著的大量冗余檢測出，減少挖掘資源的浪費，從而增加了挖掘結果的有效性。

傳統的聚類方法都對原始數據計算它們之間的距離來得到相似度，然后通過相似度進行聚類，這樣的方法對于低維數據有良好的效果，但是對于高維數據卻不能產生很好的聚類效果，因為高維數據的分布有其特殊性。通過超圖模型的分割實現對高維數據的聚類卻能產生較好的效果。它先將原始數據之間關系轉化成超圖，數據點表示成超圖的節點，數據點間的關系用超邊的權重來表示。然后對超圖進行分割，除去相應的超邊使得權重大的超邊中的點聚于一個類中，同時使被除去的超邊權重之和最小。這樣就通過對超圖的分割實現了對數據的聚類。具體的算法流程如下。

首先，將數據點之間的關系轉化為超圖，數據點表示為超圖節點。如果某幾個數據點的支持度大于一定閾值，則它們能構成一個頻繁集，就將它們用一條超邊連接，超邊的權重就是這一頻繁集的置信度，重復同樣的方法就可以得超邊和權重。

然后，在基礎此上，通過超圖分割實現數據的聚類。若設將數據分成k類，則就是對超圖的k類分割，不斷除去相應的超邊，直到將數據分為k類，且每個分割中數據都密切相關為止，同時保持每次被除去的超邊權重和最小，最終得到的分割就是聚類的結果。

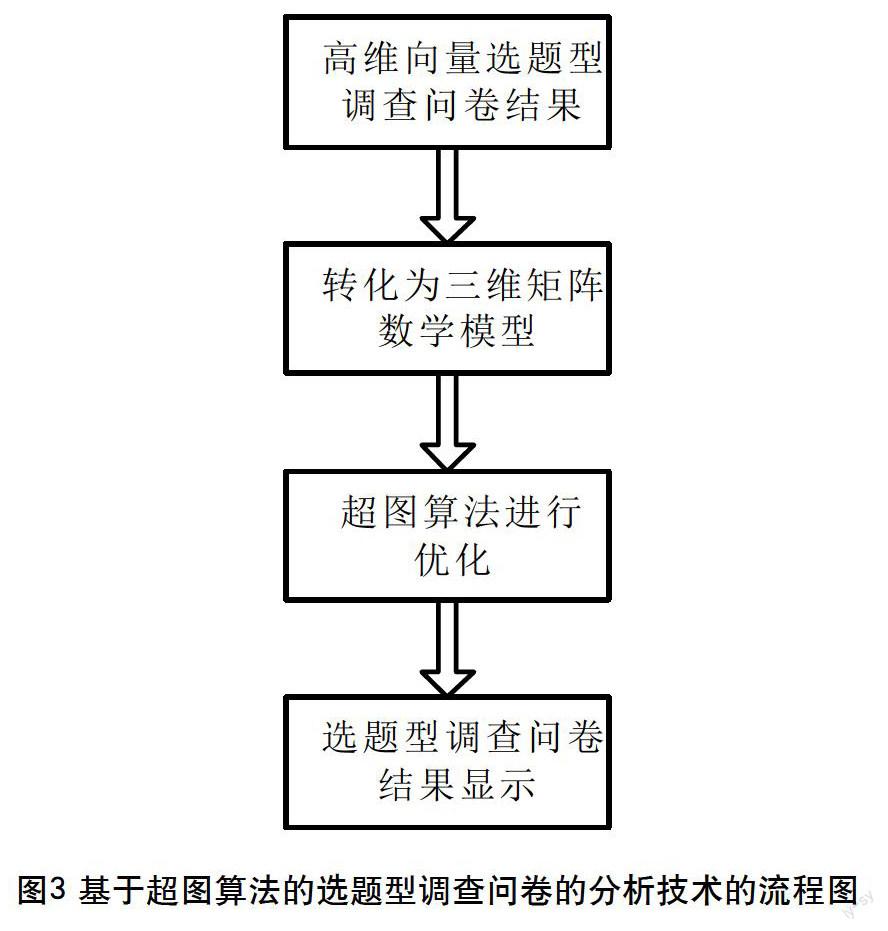
如圖3所示是基于超圖算法的選題型調查問卷的分析技術的流程圖，主要包括4個主要部分，一是用向量表示調查問卷結果，二是將向量表示的調查問卷轉化為三維矩陣數學模型表示調查問卷結果，三是使用超圖算法進行優化，四是根據要求顯示調查問卷結果。

4 結語

該文針對社會調查數據處理與分析中存在的問題，建立了基于三維矩陣的數學模型，將單選題和多選題表示成向量，將排序題表示成多個列向量，從而每一題可以表示成空間的一個維度，每一個向量就是一個元素，這樣每一張問卷就可以表示成一個矩陣，通過將多個矩陣疊加就可以得到三維矩陣。該數學模型可以利用三維矩陣的性質對其進行多種數學處理，如豎切、橫切、像素化后投影等。在數學處理的基礎上，該文又提出超圖理論對數據進行聚類和檢測冗余規則的分析。

參考文獻

[1] 陳慧萍，王煜，王建東.高維數據挖掘算法的研究與進展[J].計算機工程與應用，2006（24）：170-173.

[2] 張東.基于VFP的調查問卷通用統計匯總生成系統的設計與實現[J].科技資訊，2006（10）：183.

[3] 奚維吉.用戶滿意度調查的數據處理[J].科技資訊，2007（8）：253-254.

[4] 崔陽，楊炳儒.超圖在數據挖掘領域中的幾個應用[J].計算機科學，2010，37（6）：220-222.

[5] 朱玉全，楊鶴標，孫蕾.數據挖掘技術[M].南京：東南大學出版社，2006.

[6] 王志平，王眾托.超網絡理論及其應用[M].北京：科學出版社，2008.

[7] Jong Soo Park，Ming-Syan Chen，Philip S.Yu.Using a hash-based method with transaction trimming for mining associationrules [J].IEEE Transactions on knowledge and engineering，1997，9（5）：813-825.

[8] 王海英，黃強，李傳濤，等.圖論算法及其 MATLAB實現[M].北京航空航天大學出版社，2010.

[9] H.Toivonen. Sampling large databases for association rules [C]// Proc. 1996 Int. Conf. Very Large Data Bases （VLDB'96）.1996.

[10] Marco Dorigo， Vittorio Maniezzo， Alberto Colorni. The ant system： optimization by a colony of cooperative agents [J].Physical Review Letters，1995，75（14）：2686-2689.

[11] S. Brin， R. Motwani， J. D.Ullman，et al.Dynamic itemset counting and implication rules for market basket data [J].ACMSIGMOD Record，1997，26（2）：255-264.

[12]金欣磊，馬龍華，吳鐵軍，等.基于隨機過程的 PSO 收斂性分析[J].自動化學報，2007，33（12）：1263-1268.

[13]Van de Bergh F， A P Engelbrecht. A study of particle swarm optimization trajectories [J].Information Sciences， 2006，17（6）：937-971.