數學思想推動證明思路

王軍

證明是判斷一個命題是真命題的推理過程，有利于培養人的思維品質，培養人的推理意識，是中考命題的重要考點，主要考查對證明推理過程的理解和邏輯推理的能力，題型有選擇題、填空題和解答題.

證明中的推理過程不能“想當然”，每一步推理都要有根據.這些根據，可以是已知條件，也可以是定義、定理和公理，推理過程要嚴密. 證明中的邏輯推理離不開數學思想，數學思想有助于尋找邏輯推理的依據和途徑.

一、 方程思想的應用

在處理兩條直線的平行問題時，我們經常會遇到角的關系問題，而這種角的關系又通常需要利用一個等式才能顯現出來，其中也離不開方程.

例1 如圖1，若a∥b，∠1=3x+70°，∠2=2x+80°，則x=______，∠3=______.

解：若a∥b，可得：∠1=∠2 （因為∠1與∠2的對頂角是同位角），

所以可得： 3x+70°=2x+80°，

解得：x=10°，

即：∠3=180°-∠1=180°-100°=80°.

【點評】本題根據平行線的性質得出圖形中角與角之間的數量關系，并通過方程求出x的大小，進而使問題獲解.

二、 轉化思想的應用

有些數學題目，初看覺得無從下手，但若能轉化解題思路，問題便能得到順利解決.

例2 如圖2，AB平行EF，BC垂直CD于C，∠ABC=30°，∠DEF=45°，求∠CDE的大小.

【解析】本題的條件中雖然給出了平行線與垂直，還給出了兩個具體角的大小，但好像還是與要求的角無關，考慮有平行線，想到可將問題轉化，于是，過點C和D作平行線，這樣就可分別將要求的角轉化到已知角中去.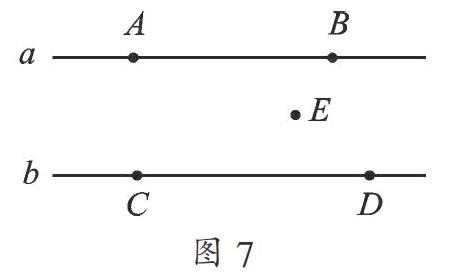

解：分別過點C，D作CM∥AB，DN∥AB，

由AB ∥ EF，得到AB ∥ CM ∥ DN∥ EF，

∴∠ABC=∠BCM=30°，∠DEF=∠GDE=45°，∠MCD=∠CDG.

∵BC⊥CD，∴∠BCD=90°，

∴∠MCD=∠CDG=60°，

∴∠CDE=∠CDG+∠GDE=105°.

【點評】熟練掌握平行線的條件和特征，并能靈活運用是求解本題的關鍵，充分運用條件，及時利用輔助線將問題轉化是正確求解的前提.另外，對于兩條平行線間的“折線”與“拐角”的問題，一般都是在拐點處作平行線，使問題轉化，從而構造出一些相等的角或互補的角，使已知與未知一目了然，達到解題的目的.

三、 整體思想的應用

從問題的整體著手進行思考，往往會使問題的解答快捷，迅速，可以培養同學們思維的敏捷性.

例3 已知在四邊形ABCD中，∠A=∠C=90°.

（1） ∠ABC+∠ADC=_______；

（2） 如圖3，若DE平分∠NDC的外角，BF平分∠ABC的外角，請寫出DE與BF的位置關系，并證明.

（3） 如圖4，若BE、DE分別四等分∠ABC、∠ADC的外角（即∠CDE=∠CDN，∠CBE=∠CBM），試求∠E的度數.

【解析】（1） 根據四邊形內角和等于360°列式計算即可得解；

（2） 延長DE交BF于G，根據角平分線的定義可得∠CDE =∠ADC，∠CBF =∠CBM，然后求出∠CDE=∠CBF，再利用三角形的內角和定理求出∠BGE=∠C=90°，最后根據垂直的定義證明即可；

（3） 先求出∠CDE+∠CBE，然后延長DC交BE于H，再根據三角形的一個外角等于與它不相鄰的兩個內角的和求解即可.

解：（1） ∵∠A=∠C=90°，

∴∠ABC+∠ADC=360°-90°×2=180°，

故答案為：180°；

（2） 延長DE交BF于G，

∵DE平分∠ADC，BF平分∠CBM，

∴∠CDE=∠ADC，∠CBF=∠CBM，

又∵∠CBM=180°-∠ABC=180°-（180°-∠ADC）=∠ADC，

∴∠CDE=∠CBF，

又∵∠BED=∠CDE+∠C=∠CBF+∠BGE，

∴∠BGE=∠C=90°，

∴DG⊥BF，即DE⊥BF；

（3） 由（1）得：∠CDN+∠CBM=180°，

∵BE、DE分別四等分∠ABC、∠ADC的外角，

∴∠CDE+∠CBE=×180°=45°，

延長DC交BE于H，由三角形的外角性質得，∠BHD=∠CDE+∠E，∠BCD=∠BHD+∠CBE，

∴∠BCD=∠CBE+∠CDE+∠E，

∴∠E=90°-45°=45°.

【點評】本題考查了三角形的內角和定理，四邊形的內角和定理，角平分線的定義，三角形的一個外角等于與它不相鄰的兩個內角的和的性質，熟記各性質是解題的關鍵，要注意整體思想的利用.

四、 分類討論思想的應用

數學中的許多問題由于題設交代籠統，需要進行討論；另外由于題意復雜，包含情況比較多，也要進行討論.分類是按照數學對象的相同點和差異點，將數學對象分為不同種類的方法，其目的是使復雜問題簡單化.

例4 設直線a∥b，在a上任取兩點A，B，在直線b上任取兩點C，D，再在兩平行線之間任取一點E，試判斷∠BED，∠ABE，∠EDC之間有何關系？請猜想并證明你的結論.

【解析】連接線段BD，考慮到E點與BD之間的位置關系：點E可能在BD上，也可能在線段BD的左側，還可能在線段BD的右側，故解答此問題應注意分三種情況進行討論

解：連接BD.

（1） 當E點在線段BD上時，這時∠BED=180°，∠ABE+∠EDC=180°（兩直線平行，同旁內角互補），所以∠BED=∠ABE+∠EDC；

（2） 當點E在線段BD的左側時，過E點作EF∥AB，交BD于F，所以EF∥CD（平行公理的推論），所以∠BEF=∠ABE，∠FED=∠EDC（兩直線平行，內錯角相等），所以∠BEF+∠FED=∠ABE+∠EDC（等量性質），即∠BED=∠ABE+∠EDC；

（3） 當點E在線段BD的右側時（解略）.

【點評】利用分類討論思想解題時，需要認真審題，全面考慮，要做到不重不漏.

（作者單位：江蘇省連云港市贛榆外國語學校）