直通式真空集熱管熱性能的數值模擬研究

仇秋玲， 匡　蕘， 楊　帆， 劉靜靜

(東南大學 能源與環境學院， 南京 210096)

?

新能源

直通式真空集熱管熱性能的數值模擬研究

仇秋玲， 匡蕘， 楊帆， 劉靜靜

(東南大學 能源與環境學院， 南京 210096)

摘要：利用Fluent軟件對直通式真空集熱管復雜的耦合換熱過程進行了數值模擬，建立了集熱管的非均勻熱流邊界條件下的傳熱模型，并將模擬結果與實驗結果進行對比驗證；分析得到了非均勻熱流邊界條件下，輻照強度、傳熱工質流速和入口溫度對吸熱管周向溫度分布的影響。結果表明：吸熱管軸向熱流分布極不均勻，吸熱管周向溫差高達74.5 K。較大的溫差會使集熱管產生熱應力，當超過集熱管的屈服強度時，就會引起集熱管的破壞，降低使用壽命。

關鍵詞：直通式真空集熱管； 熱性能； 熱流密度； 不均勻熱流分布

直通式金屬-玻璃真空集熱管效率高、熱循環性能好、結構堅固、可規模化生產，是槽式熱發電系統中應用最廣泛的集熱元件，主要用于中高溫范疇[1]。然而反射鏡的聚光作用會使其表面產生較大的溫度梯度，致使集熱管表面產生龜裂、熱疲勞破壞。這一問題暴露了當前太陽能高溫集熱器設計與溫度控制方面存在著認識不足[2]。

20世紀開始，很多科研人員針對管內流動換熱問題開展了大量研究，提出諸多關聯式，而熱流邊界條件多為均勻熱流和均勻管壁溫。由于實驗條件的限制，科研人員對非均勻熱流邊界條件下的管內換熱問題的研究工作開展較少，且多為理論簡化分析。集熱管周向熱流密度的不均導致溫度分布也很不均勻，是造成集熱管應力集中和材料疲勞失效的主要原因。Gartner D等[3]對非線性不均勻熱流條件下集熱管內流動換熱的邊界層進行了理論研究，該方法具有一定的普遍性，但仍有很大的局限性。Reynolds W C[4-5]采用分析求解的方法得到了不均勻熱流條件下的集熱管內的層流和湍流換熱情況，求解過程假設熱流邊界為余弦分布并簡化了周向和軸向湍流熱耗散率。該方法需要查閱圖表、準確性低且不方便。

集熱管表面的熱流分布極不均勻，而大多數模型都是假定集熱管表面能流分布和流體流動均勻。為準確預測集熱管內流體流動對流傳熱情況，筆者以數值模擬得到的熱流分布為邊界條件，利用Fluent軟件對金屬-玻璃太陽能真空集熱管內流場和溫度場進行數值模擬，并與實驗數據對比驗證。通過對不同太陽輻射強度、傳熱工質流速和入口溫度工作參數下集熱管流道內的流動與換熱的數值模擬，研究周向非均勻熱流邊界條件下集熱管管壁溫度分布規律的情況。

1Fluent計算模型

1.1 物理模型的建立

周向非均勻高密度熱流引發的過熱問題一直影響著太陽能熱發電站中集熱器的運行安全。為研究不均勻熱流密度下的集熱管內溫度場分布作如下假設：(1)吸熱管和外部玻璃套管之間的環形空間高度真空，忽略對流熱損失，只考慮金屬管外表面對玻璃管內表面的輻射換熱；(2)流體不可壓縮，通過平均流速和管道直徑得出Re的范圍(8 650，43 247)，屬于完全湍流，同時假設流體處于充分發展階段，為穩態湍流，且環境溫度恒定；(3)機械跟蹤系統準確，忽略光學誤差，假定入射角修正為1。圖1為槽式直通式集熱管的簡化物理模型；集熱管為玻璃封接直通式太陽能真空集熱管，其主要特征參數見表1。

注：1)100 ℃時吸收涂層發射率為0.08；2)300 ℃時吸收涂層發射率為0.16。

1.2 數學模型的建立

Fluent的理論基礎是計算流體力學，三大基本守恒方程是求解所有流動換熱問題的基本方程，輻射傳遞方程則是求解有輻射換熱問題的基本方程。三維流動的控制方程分別為[6]：

連續方程

(1)

動量方程

(2)

能量方程

(3)

k方程

(4)

ε方程

(5)

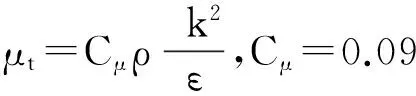
1.3 預處理

集熱管的三維模型通過前處理軟件Gambit2.3.16完成，建模尺寸跟實際尺寸相同。整個模型采用Hex/cooper方法網格離散，優點是計算準確并且計算工作量少。為準確計算集熱管內壁表面傳熱特性，對集熱管內壁表面設置邊界層。

建模時作如下假設：(1)集熱管處于穩態傳熱過程；(2)傳熱工質和吸熱管的物理參數為常數；(3)不考慮管壁和流體間的接觸熱阻；(4)忽略集熱管端部熱損失。

1.4 邊界條件設置

邊界條件的設置對模型的準確性有很大關系，現對集熱管的邊界條件設置如下：

(1) 由于不知道出口壓力和速度，且出口流動完全發展，故選擇outflow邊界條件。垂直于出口面方向上所有變量擴散通量為零，徑向允許存在物理量梯度。

(2) 集熱管端部處，分別設置為絕熱邊界條件。

(3) 玻璃管外表面是輻射和對流混合換熱，玻璃管外表面給定實驗環境溫度和玻璃管外壁的對流換熱系數。計算輻射能量時，假設玻璃套管是置于大的黑體空腔(天空)中的灰體，其對應的光學參數為常數，而天空溫度取低于實驗時環境溫度8K[7]。

(4) 由于集熱管對反射鏡的遮擋等原因，集熱管表面得到的能流分布較為不規則。為提高模型的準確性，筆者采用的集熱管表面的熱流密度分布是根據光學聚光比擬合得到的基于位置角θ的熱流密度的方程見式(6)和基于以吸收管中心為原點的XY坐標系的熱流密度的擬合公式見式(7)。

(6)

(7)

式中：q為吸收管表面的熱流密度，W/m2；Ib為當地太陽直射輻射強度，W/m2。該模擬同時采用UDF數據傳遞子程序轉換為吸收管外表面的熱流邊界條件。

2模型驗證

室外實驗的槽式太陽能集熱系統由4個集熱單元組成，每個集熱單元由4根集熱管串聯組成，所使用的集熱管參數見表1。槽式聚光集熱器的聚光比為30.56，開口寬度為5.77 m，集熱單元長度為8 m，采用東西向布置，單軸自動跟蹤方式，傳熱工質為水。實驗中流體進口溫度的測量誤差為±0.1 K，太陽輻照度的測量誤差為±50 W/m2，流體流量的測量誤差為±1%。

為了驗證耦合計算模型的正確性，模擬計算了幾組典型室外實驗方案的結果，并與實驗結果對比分析，結果見表2。

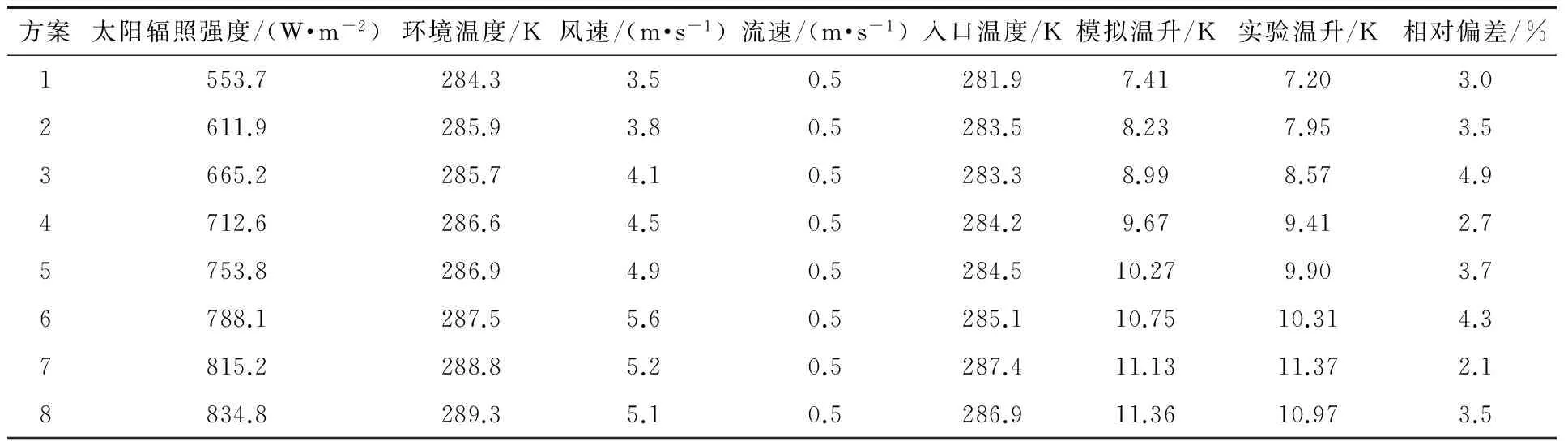
表2　模擬結果與實驗結果的數據對比

通過表2中模擬結果與實驗結果的數據對比可知：模擬溫升與實驗溫升的最大相對偏差為4.9%，平均相對偏差為3.4%，由此可見模擬結果和實驗結果吻合較好，說明該模型和模擬方法是可用的，模擬結果具有可靠性。

從表2中的數據還可以看出：同一工況下模擬得到的出口溫度比實驗得到的出口溫度略高，主要是因為模擬過程忽略了吸熱管外壁和玻璃管內壁間的對流熱損失以及簡化了集熱管端部的熱損失；同時實驗過程中不可避免的一些測量誤差也會帶來影響。

3直通式集熱管的熱性能分析

利用該耦合換熱模型對不均勻熱流密度下的集熱管進行分析，得出工質進口流速、太陽輻照強度和入口溫度對集熱管溫度分布的影響。

槽式太陽能集熱器的邊緣角為77°，集熱單元長8 m，吸熱管內徑為0.054 m、吸熱管外徑為0.060 m，幾何聚光比為30。

圖2和圖3是太陽直射輻射強度為600 W/m2，流體入口溫度為293 K，流速為0.1 m/s時集熱管的軸截面溫度和速度分布圖。

圖4和圖5為吸熱管外壁熱流和溫度分布圖。

從圖中可以看出：吸熱管表面的熱流密度非常不均勻，最大有44 000 W/m2，最低只有2 000 W/m2，使得吸熱管溫度分布在徑向和周向也極不均勻，但速度分布基本不受能流密度影響。沿流動方向管壁周向溫差越來越大，這是因為流體入口溫度較低，吸熱能力強，及時吸收大量的熱量，使管壁溫升小，周向溫差也小。沿流動方向隨著流體溫度升高，換熱能力降低，但是下表面較大的輻射強度不變，管壁溫度上升較快，導致周向溫差增大。可以推斷，對于大型的聚光集熱系統，集熱管在不均勻的高能流密度下，周向存在較大的溫差，引起的熱膨脹造成吸熱管的變形甚至破壞。

圖6給出了輻照強度為600 W/m2、集熱管入口溫度為293 K時，不同入口流速時的集熱管周向溫度分布曲線。由于集熱管形狀和受熱情況左右是對稱的，所以只分析了右半圓的溫度分布情況。可以看出吸熱管外表面的周向溫度分布規律與集熱管周向能流密度分布規律是一致的。工質流速對集熱管的溫度分布影響較大，隨著流速的增大，Re增大，擾流強度隨之增強，流體域壁面的傳熱受到強化，起到了強化換熱的效果。當流速從0.1 m/s增加到0.2 m/s時，吸收管外壁的最大溫差由74.5 K降低到45.8 K。隨著流速的增大，吸收管壁的最大溫差逐漸減小。

圖7給出了集熱管入口溫度為293 K、工質流速為0.2 m/s時，不同太陽輻照強度條件下的集熱管周向溫度分布曲線。可以看出：太陽輻射對壁面溫度分布的影響非常明顯，當輻照強度從600 W/m2增大到1 000 W/m2時，吸收管的外壁溫差從45.9 K上升到了75.8 K。太陽直射輻射越大，經聚光后造成的上下表面的能流差越大，使集熱管管壁的溫差也越大。當大型的槽式集熱器在室外運行時，受到天氣的實時變化影響，集熱管壁的溫差也在不斷變化，產生熱應力，吸熱管反復的承受溫度循環，最終會導致吸熱管的疲勞損壞。

圖8給出了集熱管工質流速為0.2 m/s、輻照強度為800 W/m2時，不同入口溫度時集熱管的周向溫度分布圖曲線。可以看出：流體的入口溫度對集熱管的周向溫差影響不是很大，當入口溫度分別為283 K、293 K、303 K時，吸收管外壁最大溫差分別為60.7 K、60.9 K、61.2 K。可見對于以水為工質的集熱管在過冷段，尤其對于高聚光比的集熱器，為避免吸收管出現過高的溫差，引起集熱管的過熱甚至損壞，應選擇合適的入口流速，控制溫差在集熱管可以接受的范圍內。

4結語

運用Fluent軟件建立了槽式太陽能集熱管的傳熱流動數學模型，采用集熱管表面的熱流密度分布是根據光學聚光比擬合得到的能流分布函數，作為吸熱管外壁上的能流邊界條件，主要目的是得到集熱管在實際復雜條件下運行時的溫度分布特性。模擬結果表明：

(1) 太陽直射輻射強度為600 W/m2、流體入口溫度為293 K、流速為0.1 m/s時，吸熱管表面的熱流密度非常不均勻，最大有44 000 W/m2，最

低只有2 000 W/m2，使得吸熱管溫度分布在徑向和周向也極不均勻，但速度分布基本不受能流密度影響，而沿流動方向管壁周向溫度差值越來越大。

(2) 輻照強度為600 W/m2、集熱管入口溫度為293 K時，當流速從0.1 m/s增加到0.2 m/s時，吸收管外壁的最大溫差由74.5 K降低到45.8 K。隨著流速的增大，吸收管壁的最大溫差逐漸減小。

(3) 集熱管入口溫度為293 K、工質流速為0.2 m/s時，當輻照強度從600 W/m2增大到1 000 W/m2時，吸收管的外壁溫差從45.9 K上升到了75.8 K。太陽直射輻射越大，經聚光后造成的上下表面的能流差越大，使集熱管管壁的溫差也越大。

(4) 集熱管工質流速為0.2 m/s、輻照強度為800 W/m2時，當入口溫度分別為283 K、293 K、303 K時，吸收管外壁最大溫差分別為60.7 K、60.9 K、61.2 K。由此可見，對于高聚光比的集熱器，應選擇合適的入口流速，控制溫差在集熱管可以接受的范圍內。

參考文獻：

[1] 王軍, 張耀明, 張文進, 等. 槽式太陽能熱發電中的聚光集熱器[J]. 太陽能, 2005(4): 25-29.

[2] Litwin R. Receiver system: lesson learned from Solar Two[R]. New Mexico and Livermore，California: Sandia National Laboratories, 2002.

[3] Gartner D, Johannsena K, Ramm H. Turbulent heat transfer in a circular tube with circumferentially varying thermal boundary conditions[J]. International Journal of Heat and Mass Transfer, 1974, 17(9):1003-1018.

[4] Reynolds W C. Heat transfer to fully developed laminar flow in a circular tube with arbitrary circumferential heat flux[J]. Journal of Heat Transfer, 1950, 82(2): 108.

[5] Reynolds W C．Turbulent heat transfer in a circular tube with variable circumferential heat flux[J]．International Journal of Heat and Mass Transfer, 1963, 6(6)：445-454．

[6] Wang K, He Y L, Cheng Z D. A design method and numerical study for a new type parabolic trough solar collector with uniform solar flux distribution[J]. Science China Technological Sciences, 2014, 57(3): 531-540.

[7] Forristall R. Heat transfer analysis and modeling of a parabolic trough solar receiver implemented in engineering equation solver [R]. Golden, USA: National Renewable Energy Laboratory, 2003.

Numerical Simulation on Thermal Performance of Straight-through Evacuated Collector Tubes

Qiu Qiuling, Kuang Rao, Yang Fan, Liu Jingjing

(School of Energy and Environment, Southeast University, Nanjing 210096, China)

Abstract：The complex coupling heat transfer process of collector tubes was simulated using Fluent software based on the heat transfer model established under the boundary condition of non-uniform heat flux, following which the simulation results were verified by comparison with experimental data. Meanwhile, the effects of irradiation intensity, heat-transfer fluid velocity and inlet temperature on the circumferential temperature distribution around absorber tubes were analyzed under the boundary condition of non-uniform heat flux. Results show that the axial distribution of heat flux is very uneven and the circumferential temperature difference around absorber tubes is up to 74.5 K. Larger temperature difference would bring thermal stress in the collector tube, and when the stress exceeds the yield strength of collector, it would cause damage to the tube, thus reducing its service life.

Keywords：straight-through evacuated collector tube; thermal performance; heat flux; non-uniform heat flux distribution

收稿日期：2015-10-19

作者簡介：仇秋玲(1990—)，女，在讀碩士研究生，主要從事太陽能集熱器的熱性能研究。E-mail: qiulingjiayou@163.com

中圖分類號：TK515

文獻標志碼：A

文章編號：1671-086X(2016)03-0148-05