基于Shapley值-仿真技術的工序工期預測

申建紅，　孫小寧，　張云華

(青島理工大學　管理學院， 山東　青島　266520)

?

基于Shapley值-仿真技術的工序工期預測

申建紅，孫小寧，張云華

(青島理工大學管理學院， 山東青島266520)

摘要：針對傳統工期預測方法中對工序工期影響因素間相關性考慮不足的缺陷，利用隨機數仿真工序工期影響因素的不確定性和Shapley值函數計算多因素間相關性的原理，將仿真技術和Shapley值函數相結合，計算出影響因素對工期的綜合影響系數。并且根據每道工序工程量與單位時間完成工程量的比值準確計算出每道工序的理想化工期。在此基礎上利用工期綜合影響系數對其進行調整，建立一種新的工期預測模型。最后，以工程實例對工期預測模型進行驗證，并建立4DBIM進度模型對施工進度進行三維可視化模擬對比，結果表明，文中方法對施工工期的預測效果精確，具有較好的實際指導意義。

關鍵詞：工期預測；仿真技術；Shapley值；BIM

伴隨著經濟的發展和工程技術水平的提高，現代工程項目日趨大型化和復雜化加大了工程工期預測的難度。科學合理的工期預測方法是預防工程延誤的重要手段。對此，國內外學者進行了大量的研究。?kmen等[1]考慮工期影響因素發生的不確定性，使用隨機數仿真技術對其進行研究；Ahuja[2]等開發了一種基于CPM的工期預測模型，通過估計影響因素對工序的不確定影響，預測項目工期；Salem[3]等提出工程項目的進度具有不確定性，依據多元線性回歸模型與神經網絡系統，對工程項目工序進度進行預測分析；國內學者[4～6]分別采用模糊網絡分析方法、灰色系統理論方法、灰色Verhulst方法對工期影響因素的不確定性進行研究。但上述研究均對影響因素間的相關性考慮不足。而Wang等[7]提出運用隨機數仿真影響因素對工期的影響值，證明了考慮影響因素間相關性的重要性；李軍輝等[8]基于工期影響因素的不確定性和相關性，采用影響因素相關矩陣和隨機數對工程工期仿真模擬,同時證明考慮影響因素不確定性和相關性的工期預測方法比只考慮因素不確定性的方法更加準確；但其只考慮了兩種影響因素間的相互影響,并沒有考慮多種影響因素間的相互影響。

對上述傳統工期預測方法的研究表明，在進行工期預測時，對工期的不確定性及相關性進行綜合考慮，是準確預測工期的關鍵。基于此，本文考慮了多種影響因素間的相互影響,采用Shapley值函數對工期影響因素的相關性進行分析，并與利用隨機數仿真影響因素的方法相集成建立了工期預測模型；將文中建立的工期預測模型、傳統只考慮兩種因素相關性的工期預測模型，借助BIM技術，建立各自的BIM計劃進度模型，與BIM實際進度模型進行三維對比，以驗證文中方法的準確性。

1工期預測模型的構建

工期的影響因素有很多，歸納起來主要包括人的因素(r1)，物資供應(r2)，資金供應(r3)，設計變更(r4)，技術水平(r5)，氣候因素(r6)等六大因素。這些影響因素自身具有不確定性，各因素之間又存在相關性。本文主要針對上述六種影響因素建立其體現影響因素的不確定性和多種影響因素間的相關性的施工工期預測模型。

1.1構建工期預測模型

1.1.1影響效果矩陣

各影響因素對工期的影響可能導致3種結果，即提前完工、正常完工、延誤完工。各種結果預期的概率分布范圍可以由專家根據歷史統計資料獲得。經研究表明[9]在各種因素影響下的工期服從正態分布，通過由隨機數產生器產生服從正態分布的滿足(0,1)之間的隨機數，仿真影響因素出現的概率大小G1n(g1,g2,…,gn)；將此概率大小與預期的概率分布范圍相比較，假設影響因素隨機數間于“比預期結果好”的區間內，則表明工期提前完成；經比較可得出影響因素隨機數產生的預期結果，表達式為：

(1)

則某施工段的n項影響因素的影響效果組成影響效果矩陣為Qn1=[q1,q2,…,qn]T。

1.1.2Shapley值函數

Shapley值函數[10]是合作博弈中重要的分配指標之一，它能夠實現聯盟總體利益在各成員之間的有效分配，該方法包含了屬性間的相互作用，即包含了多因素間的相關性，模型表達式為：

(2)

式中：φi(υ)表示其它因素影響下的第i種影響因素的權重；|s|表示s聯盟中的影響因素個數；υ(s)表示聯盟s的效益；υ(s/i)表示聯盟s中出去成員i后可取得的效益；w(|s|)表示這種貢獻的加權因子；υ(s)-υ(s/i)表示因素i在每個包含因素的聯盟s中的邊際貢獻率。將式(2)得出的φi(υ)組成權重矩陣為：

(3)

所得ψnn則為考慮影響因素不確定性和多因素間相關性下影響因素的權重。它作為模型中影響程度矩陣，用以代替傳統只考慮兩種因素間相關性的工期預測方法中相關系數矩陣與影響度矩陣的乘積。

1.1.3建立工期預測模型

本文首先假設各種影響因素的影響度為零的情況下，利用每道工序工程量與單位時間完成工程量的比值準確計算出每道工序工期，將此工期作為理想化目標工期TM；然后利用Shapley值考慮多因素間的相互作用的原理計算出各因素在其他因素影響下的權重，將其結果與隨機數仿真工期影響因素結合，計算出影響工期的各因素綜合影響系數；最后將理想化目標工期TM進行調整計算出預測工期TY。根據上述思路，本文建立的工期預測模型為：

(4)

式中:k代表施工工序；TY表示預測工期；TM表示理想化目標工期；tyk表示第k道工序預測工期；tmk表示第k道工序理想化目標工期；G1n、ψnn、Qn1表示工期綜合影響系數。

該模型運用隨機數仿真工期影響因素,考慮了多個影響因素間的相關性,為進一步考慮工期影響因素相關性的計算奠定了基礎。

1.24DBIM模型進度對比

BIM(Building Information Modeling,即建筑信息模型)是創建并利用數字化模型對建設項目進行設計、建造及運營的全過程的管理、優化的方法和工具[11]。首先建立工程的3DBIM模型。分別利用文中工期預測方法和傳統只考慮兩種影響因素間相關性的工期預測方法計算出每道工序的工期,然后根據各工序前后的邏輯關系繪制出整個工程的進度計劃；將進度計劃作為一個時間緯度與3DBIM實體模型相關聯，通過軟件將空間和時間兩種信息整合到一個可視的4DBIM模型中，可以直觀地預演整個施工過程[12]，最后將兩種BIM計劃進度模型和BIM實際進度模型作對比。

2工程案例

2.1工程概況及BIM模型

本工程為陽光家苑27號綜合樓，總建筑面積25019.68 m2,占地面積1787.12 m2，建筑高度為42.5 m，地下一層，地上11層，主體為剪力墻結構，基礎為筏板基礎。3DBIM建筑模型如圖1，項目目標總工期為 436 d。本案例以首層為例，考慮工程影響因素不確定性和相關性的情況下對首層進行研究。在不考慮影響因素對工期影響的前提下,計算得出首層的理想化目標工期TM為26 d。合同工期TC為33 d。首層每道工序的理想化目標工期tm分別為1、3、2、3、5、7、5 d。施工進度橫道圖見圖2,本工程為已完工工程。

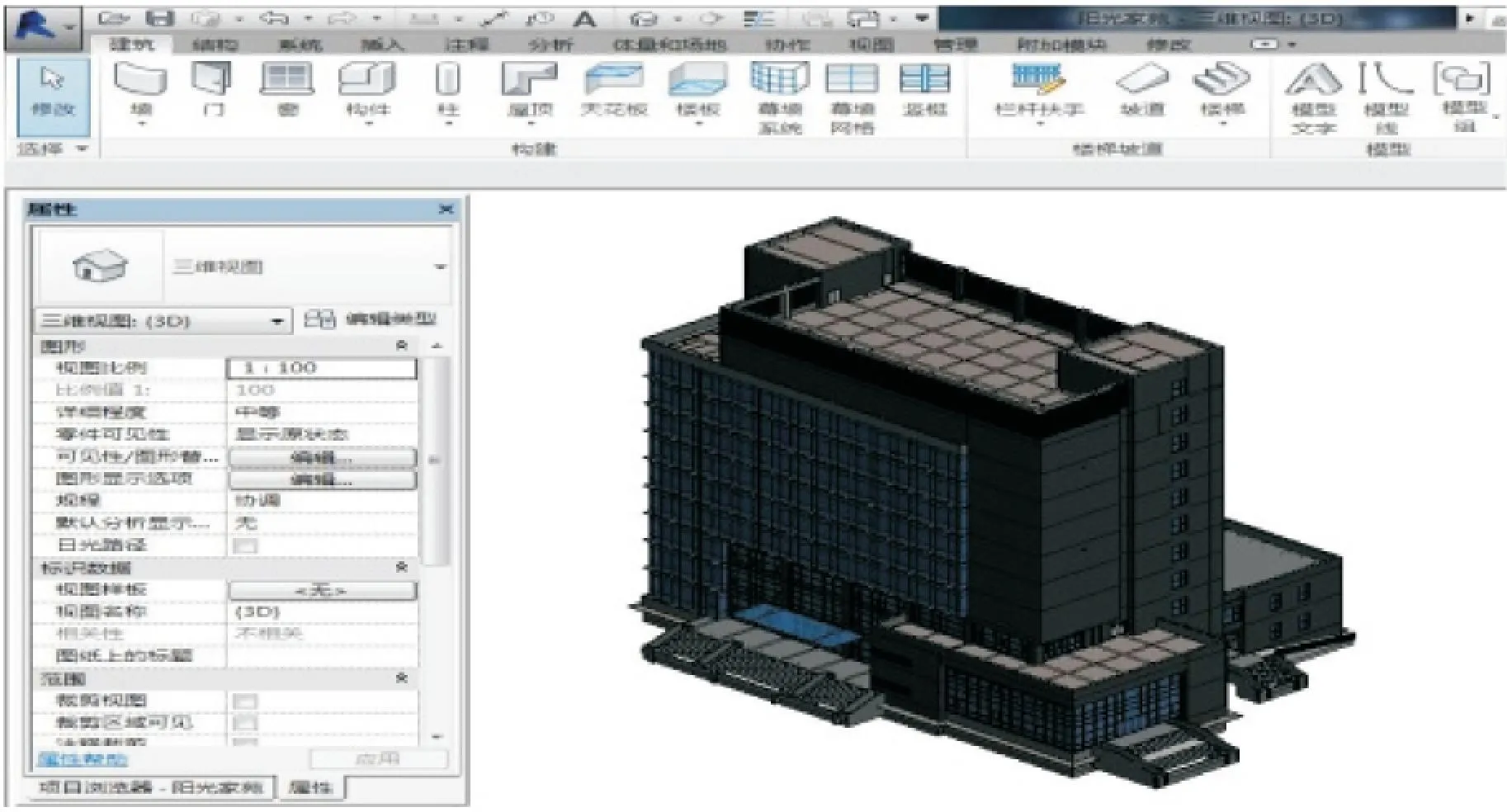
圖1　3DBIM模型

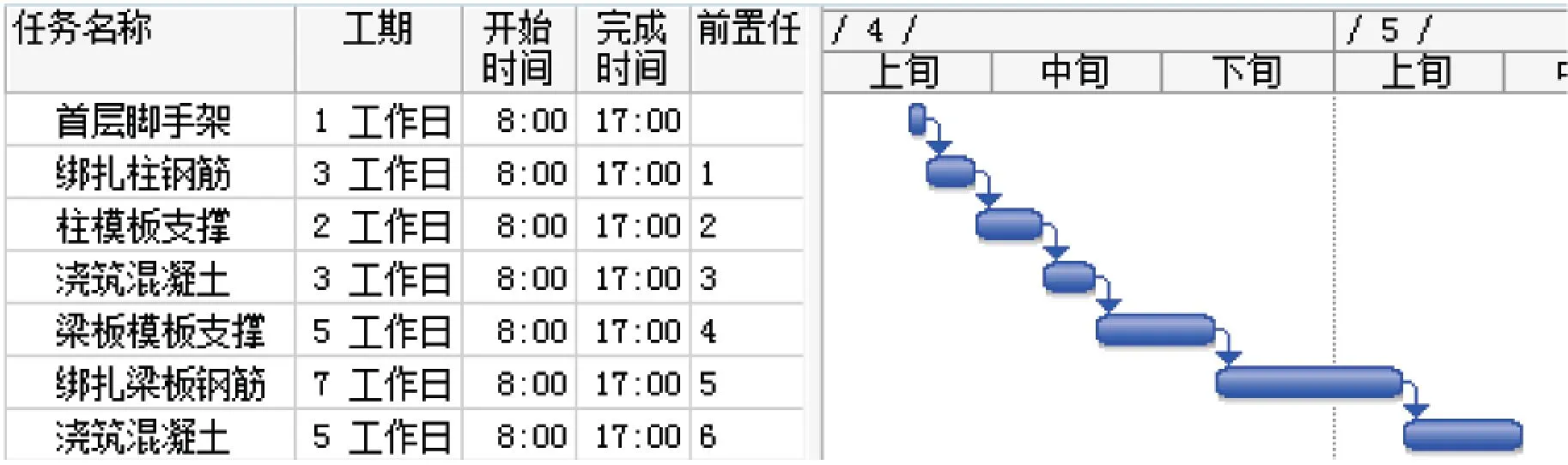
圖2　理想狀態下進度計劃橫道圖

2.2工序工期預測模型

2.2.1影響因素參數設定

根據首層綁扎柱鋼筋工序實際情況，由專家結合眾多工程歷史數據,歸納總結出各影響因素不同的概率分布范圍內產生的影響結果,用于對隨機數進行量化(表1)。

表1　影響因素概率分布范圍

2.2.2影響因素隨機數矩陣

利用隨機數產生器產生(0,1)之間的服從正態分布的隨機數，并且使每組隨機數的個數等于影響因素的個數。由產生器產生的第一組隨機數為：

G1×5=[0.3780.0570.3920.7810.8570.345]，將該組隨機數與表1進行比較，根據式(1)得到第一組影響效果矩陣為：Q5×1=[ 0-10110 ]T，同理可以得到若干組隨機數和影響效果矩陣，本文選用1000組，隨機數和影響效果矩陣如表2所示。

2.2.3因素影響度矩陣和工序工期預測

由專家結合相關資料對首層綁扎柱鋼筋工序施工時可能遇到的影響因素的權重進行打分，分別得出單因素影響度的大小和多因素相互影響下對工程首層綁扎柱鋼筋工序的權重大小，原則為六種影響因素的權重和v1(s)+v2(s)+…+v6(s)等于1。如果多因素間存在相關性，則此多因素的權重和將大于本身之和，即v123(s)>v1(s)+v2(s)+v3(s)。如表3所示(例表中{1,2,3}表示r1、r2、r3三種影響因素相互影響下對工期的影響度大小)。

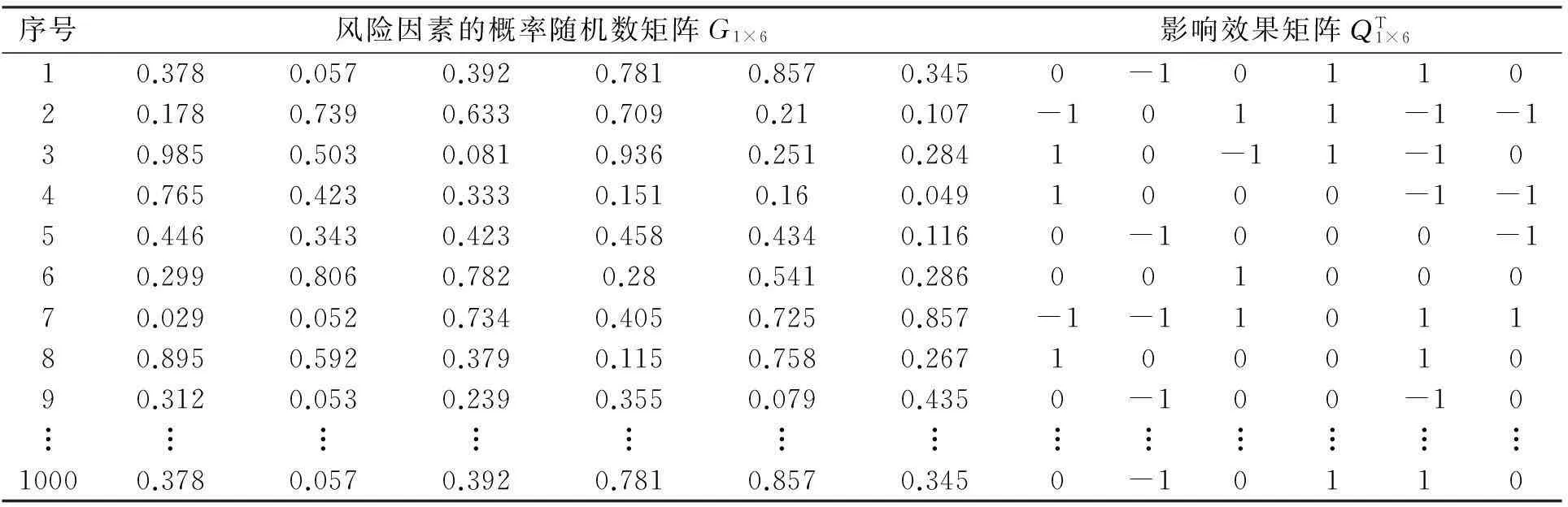
表2　隨機數矩陣和影響效果矩陣

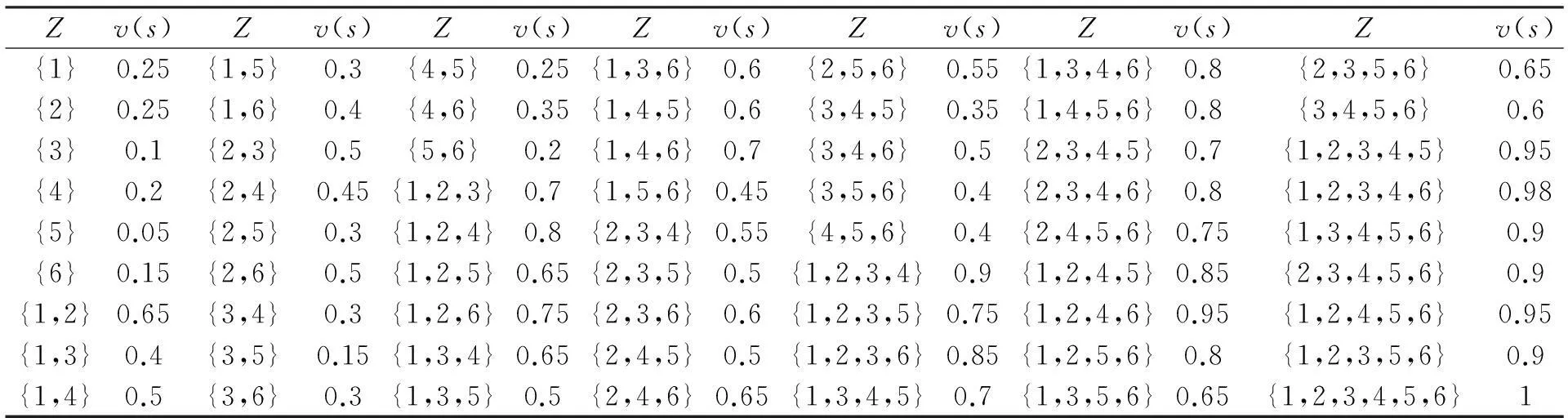
表3　因素影響度

注：Z表示影響因素的組合。

將表3數據代入式(2)中得出各因素的影響度大小(權重)分別為：φ1(υ)=0.240，φ2(υ)=0.249,φ3(υ)=0.122，φ4(υ)=0.187，φ5(υ)=0.048，φ6(υ)=0.144；得到因素影響度矩陣為：

ψ6×6=

根據以上數據，結合表2、式(4)得出的工序預測工期ty如表4所示。

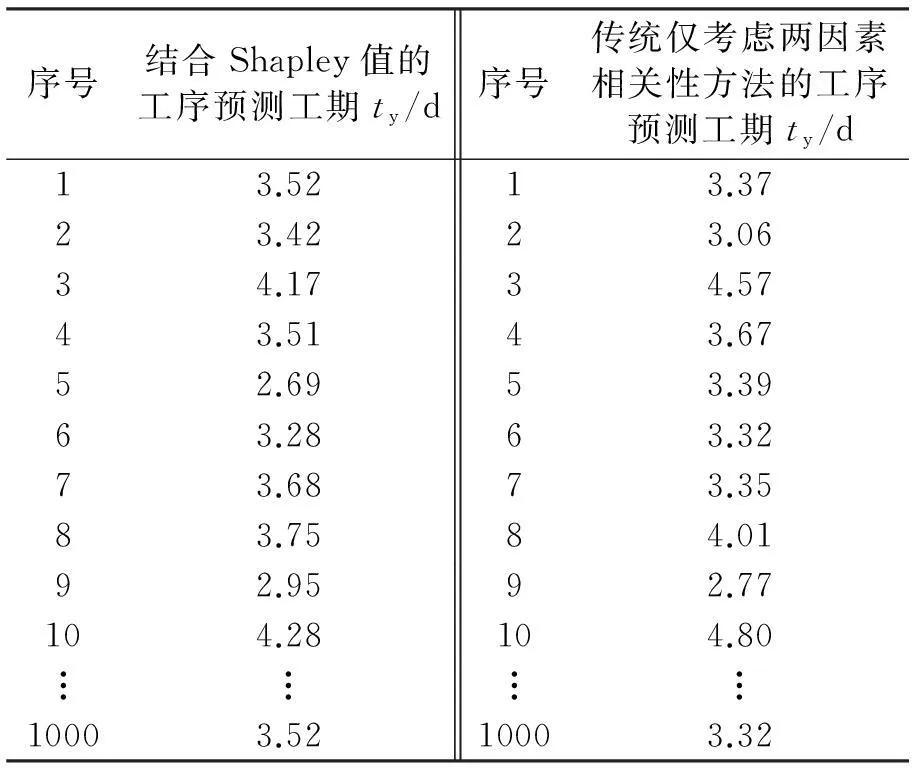
表4　工序預測工期

由上述預測結果可得出工序工期預測直方圖如圖3所示。

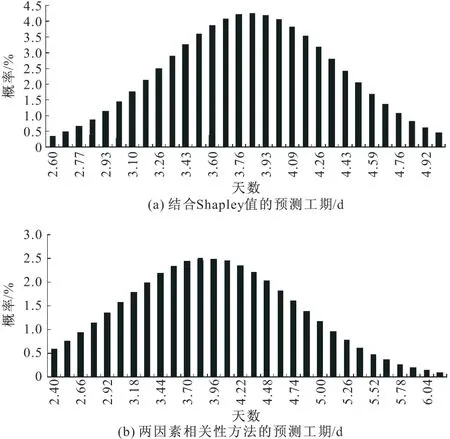
圖3　工序工期預測直方圖

經計算得結合Shapley值方法的首層綁扎柱鋼筋的工序預測工期為3.79 d，利用考慮兩因素間相關性的預測方法得出首層綁扎柱鋼筋的工序預測工期為3.86 d。對于一個標準的正態分布，其峰度系數和偏度系數分別為3和0。經計算知，結合Shapley值算法求得正態分布的峰度系數和偏度系數分別為3.23和0.43，而傳統方法求得的系數分別為3.42和0.97，且圖3b出現明顯的右拖尾現象。結果表明結合Shapley值預測的工期更加滿足正態分布。

同理，根據以上方法可以求出首層其他工序的預測工期。分別為1.26、3.79、2.52、3.64、6.3、8.82、6.3 d，首層的預測工期為32.53 d，且此工期小于合同工期。編制進度計劃如圖4所示。同理可編制出傳統只考慮兩種影響因素間相關性的預測方法的計劃橫道圖。

圖4　預測工期計劃橫道圖

2.3基于 BIM工期模擬對比控制

以文中預測方法以及考慮兩因素間相關性的預測方法分別建立4DBIM計劃進度模型(如圖5、6所示)，通過將兩種BIM計劃進度模型和BIM實際進度模型(圖7)對比，可以更直觀地展現兩種BIM計劃進度與BIM實際進度的差別。

圖5　文中方法BIM計劃進度模型

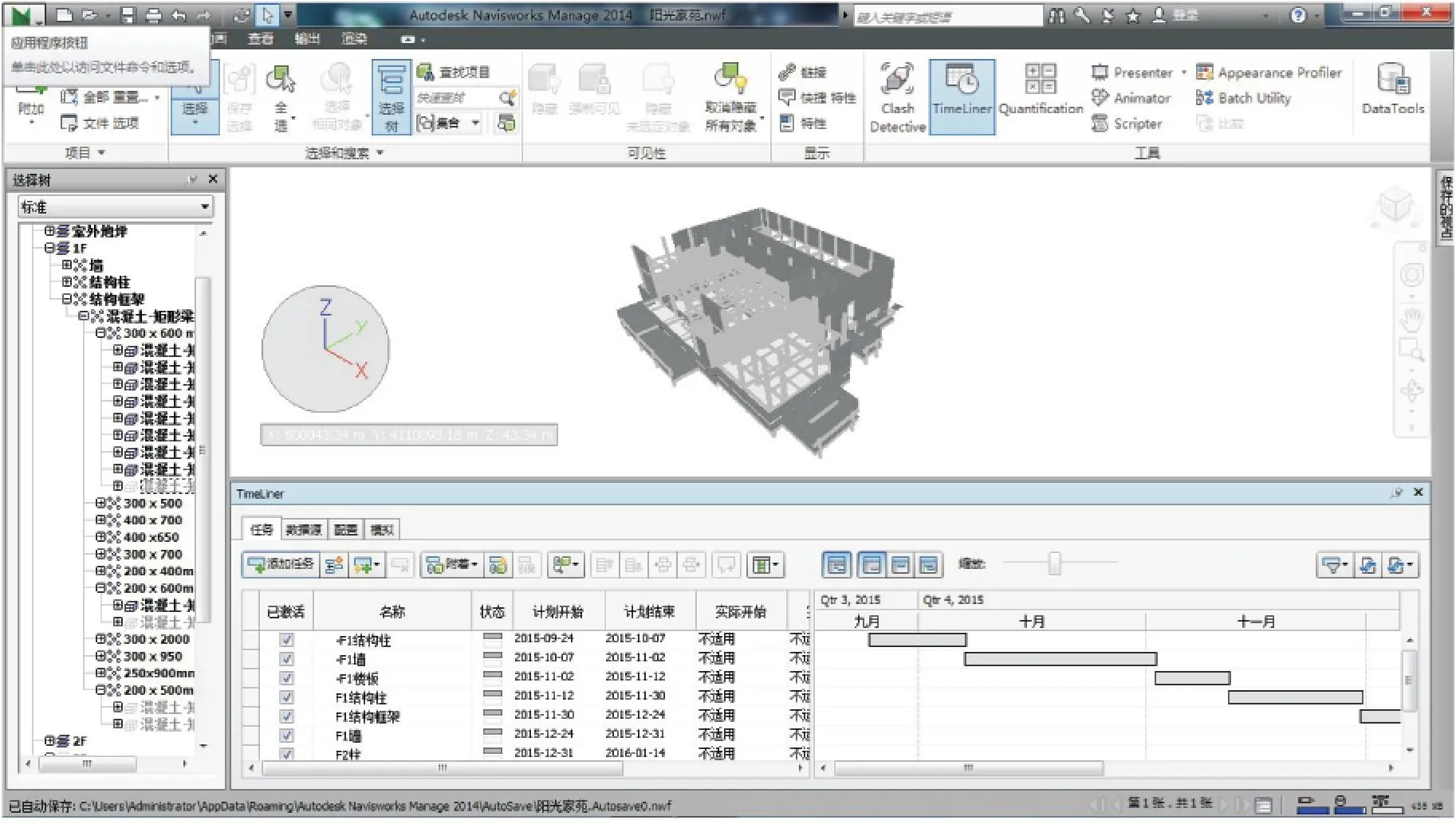
圖6　兩因素相關性方法BIM計劃進度模型

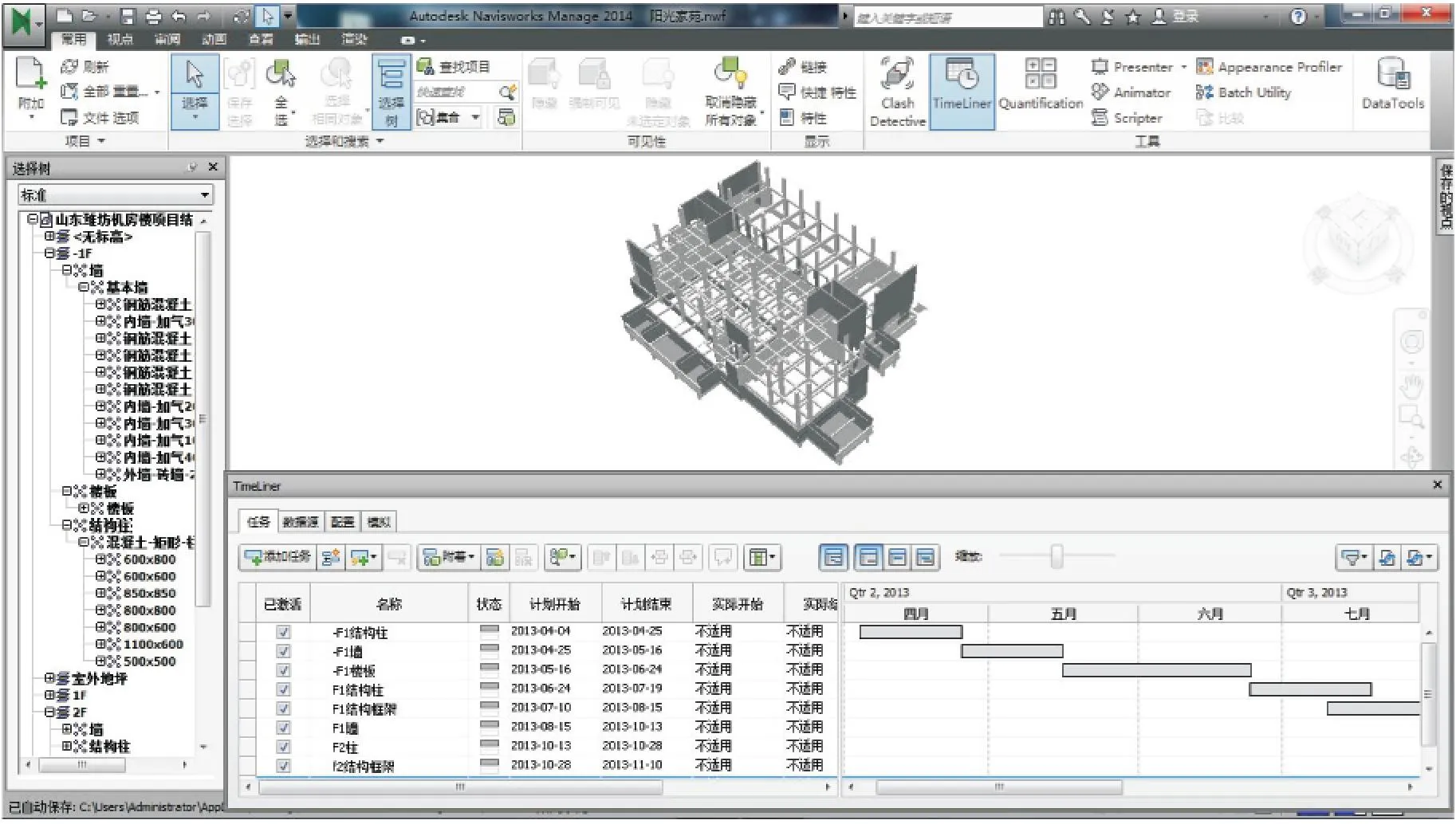
圖7　BIM實際進度模型

由上圖對比得知，文中方法預測的施工進度較傳統方法預測的施工進度更加接近實際情況，表明文中方法更加準確。

3結論

(1)考慮了多個影響因素間的相互作用，建立了基于Shapley值的工期預測模型，該模型由于考慮了多因素間的相關性，在理論上更具有合理性。

(2)建立了4DBIM模型可以直觀地對比三者可視化效果，是研究進度預測先進和有效的手段，對相關研究具有借鑒輔助意義。

(3)案例部分表明，利用隨機數仿真工程工期影響因素和Shapley值相結合的方法預測工期可行且更準確。

參考文獻

[1]?kmen?，?zta A. Construction project network evaluation with correlated schedule risk analysis model[J]. Journal of Construction Engineering and Management，2008，134(1)： 49-63.

[2]Ahuja H N，Nandakumar V. Simulation model to forecast project completion time[J]. Journal of Construction Engineering and Management, 1985，111(4)： 325-342.

[3]Salem O，Solomon J，Genaidy A，et al. Site implementation and assessment of lean con struction techniques[J]. Lean Construction Journal，2005，2(2)： 1-21.

[4]孟文清，張立寧，李萬慶. 基于模糊網絡的工程項目工期風險評估研究[J].河北建筑科技學院學報，2005，22(2)： 73-75.

[5]劉英杰. 灰色系統理論在工程進度預測中的應用[J]. 東北水利水電，2006，24(4)： 45-47.

[6]賈銘鈺，楊秀蕓，朱美潔，等. 基于掙得進度的灰色Verhulst模型對工程工期的動態預測[J]. 北京城市學院學報，2013，(5)： 32-38.

[7]Wang W C，Demsetz L A. Application example for evaluating networks considering correlation[J]. Journal of Construction Engineering and Management，2000，126(6)： 467-474.

[8]李軍輝，張云波，祁神軍，等. 基于風險相關性和隨機性的工序工期預測模型[J]. 武漢理工大學學報(信息與管理工程版)， 2010，32(6)： 1018-1021.

[9]李林,李樹丞,王道平. 基于風險分析的項目工期的估算方法研究[J]. 系統工程,2001, 19(5)： 77-81.

[10]阮愛清，劉思峰，方志耕. 基于不確定性的shapley值模型及其風險研究[J]. 統計與決策，2009，(20)： 15-17.

[11]Stephen A Jones. Introduction to BIM[EB/OL]. [2009-01-21]. http://bimhalcrow.wordpress.Com/2009/01/21/megraw-hill-construction-bim-smartmarkte-report/.

[12]王友群. BIM技術在工程項目三大目標管理中的應用[D].重慶： 重慶大學，2012.

Activity Duration Forcasting Based on Shapley-simulation Teconique

SHENJian-hong,SUNXiao-ning,ZHANGYun-hua

(School of management, Qingdao University of Technology, Qingdao 266520, China)

Abstract:Aiming at the defects that insufficient consideration of the correlation between the factors affecting the process duration in the traditional forecasting method,we use the uncertainty of the factors affecting random number simulated duration and the correlation between multiple factors of Shapley value function calculation,combine the simulation technique and Shapley function and then worke out the comprehensive influencing coefficiency of the influencing factor on the time limit. In addition,the ideal period for each process is calculated according to the ratio of the amount of each working procedure and the amount of unit time .Based on this, a new model for predicting the duration is established by using the comprehensive effect coefficient of the time limit to adjust it. Finally, the engineering projects are used to verify this model, and a 4D BIM progress model is established to simulate the construction progress. The results show that the proposed method has obvious forecast effect on the construction progress, and has better practical guiding significance.

Key words：the project duration prediction; simulation technique; shapley value; BIM

收稿日期：2015-11-28修回日期： 2015-01-04

作者簡介：申建紅(1970-)，男，山東青島人，博士，教授，研究方向為土木工程風場實測及結構抗風、工程項目管理(Email：sjhqwr@163.com)

基金項目：山東省自然科學基金(ZR2011GL021)

中圖分類號：TU72

文獻標識碼：A

文章編號：2095-0985(2016)03-0030-05