一類非線性發(fā)展方程組的隱式解析解

王　然，袁學(xué)剛,，張洪武，呂　娜

(1.大連理工大學(xué) 結(jié)構(gòu)分析和工業(yè)裝備重點實驗室，遼寧 大連116024；2.大連民族大學(xué) 理學(xué)院，遼寧 大連 116605)

?

一類非線性發(fā)展方程組的隱式解析解

王然1，袁學(xué)剛1,2，張洪武1，呂娜2

(1.大連理工大學(xué) 結(jié)構(gòu)分析和工業(yè)裝備重點實驗室，遼寧 大連116024；2.大連民族大學(xué) 理學(xué)院，遼寧 大連 116605)

摘要：研究了一類非線性發(fā)展方程組的求解問題。該方程組可用于描述由各向同性近似可壓縮neo-Hookean材料組成的圓柱管在軸向載荷作用下的軸對稱運動。首先通過變分原理導(dǎo)出了描述圓柱管徑向和軸向?qū)ΨQ運動的非線性發(fā)展方程組；然后利用行波變換將其約化為非線性常微分方程組；最后得到首次積分,進而給出了此類非線性發(fā)展方程組的隱式解析解。

關(guān)鍵詞：非線性發(fā)展方程組；超彈性圓柱管；非線性運動；隱式解析解

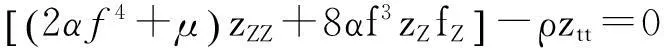
(2)

該方程組用于描述一類由各向同性近似可壓縮neo-Hookean材料組成的圓柱管在軸向載荷作用下的徑向和軸向?qū)ΨQ運動。方程組中，μ為無窮小變形的剪切模量；α為材料參數(shù)；a,b分別為圓柱管的內(nèi)、外半徑；ρ為材料密度，對于近似可壓縮材料，ρ可近似看作為常數(shù)；f,z分別為待求的變形函數(shù)，它們的下標表示對相應(yīng)變量求偏導(dǎo)數(shù)。在軸向和徑向?qū)ΨQ的變形假設(shè)下，基于柱坐標系的圓柱管變形模式為[1]：

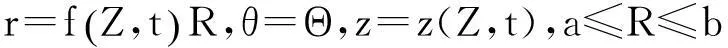
(3)

事實上，對于不同的材料、結(jié)構(gòu)以及加載模式，對應(yīng)的微分方程組也千差萬別，并且求解方法也不盡相同。目前關(guān)于超彈性軸對稱結(jié)構(gòu)已有的研究成果中，加載形式主要集中在徑向加載和軸向加載。在徑向加載方面：Knowles[2]研究了不可壓縮的Mooney—Rivlin材料組成的圓管的徑向有限振動問題，并且給出了圓管產(chǎn)生周期振動的條件以及振動周期和振幅的公式。Ren[3]研究了周期載荷作用下不可壓縮neo-Hookean材料組成的圓管徑向膨脹的動力響應(yīng)問題。Yuan等[4]研究了周期階梯加載下橫觀各向同性不可壓縮Ogden材料組成的圓管的徑向振動問題，并討論了材料參數(shù)、結(jié)構(gòu)參數(shù)以及加載模式對圓管產(chǎn)生非線性周期振動的影響。Niu等[5]研究了橫觀各向同性不可壓縮的超彈性圓柱形薄膜的動力學(xué)特性。在軸向加載方面：Coleman等[6]研究了各向同性不可壓縮neo-Hookean材料組成的圓桿的軸向運動問題，并給出了孤立波和周期波的解析表達式。Dai等[7]研究了一類由不可壓縮的改進Mooney-Rivlin材料組成的圓桿的有限軸、徑向變形問題。討論了臨界點分岔和非奇異情形，證明了扭結(jié)波的存在性。Cohen等[8]研究了一類由可壓縮Mooney-Rivlin材料組成的圓柱桿在軸向載荷作用下波的傳播問題，得到了一類用于描述圓柱桿軸對稱運動的非線性發(fā)展方程組。

1方程組的導(dǎo)出

本文考慮的圓柱管是由一類各向同性近似可壓縮neo-Hookean材料組成，應(yīng)變能函數(shù)為

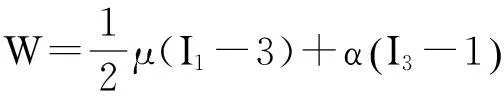
(4)

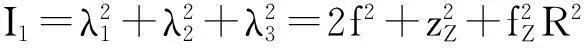
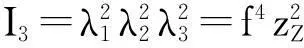
(5)

式中，I1,I3分別為右Cauchy-Green張量的第一主不變量和第三主不變量；λ1,λ2,λ3為變形梯度張量的3個主值。

基于非線性彈性理論，描述圓柱管軸向和徑向?qū)ΨQ運動的Lagrangian函數(shù)L為

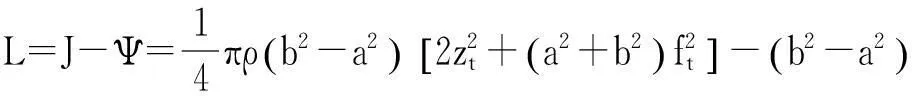
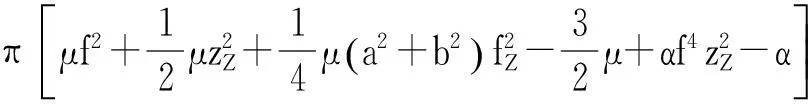
(6)

式中，J,Ψ分別為每單位長度的動能密度和勢能密度，表達式如下：

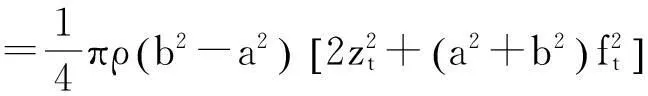
(7)

(8)

利用Hamilton原理，得到如下的Euler-Lagrange方程：

(9)

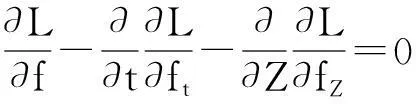
(10)

將式(6)分別代入到方程(9)和(10)，整理后得到方程(1)和(2)。

2方程組的隱式解析解

設(shè)λ為軸向伸長率zZ，作行波變換，

λ=λ(ξ),f=f(ξ),ξ=Z-ct,

(11)

式中，c為波速。

將行波變換代入到控制方程(1)和(2)，得到下面的非線性常微分方程組：

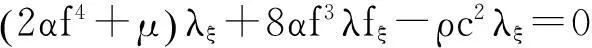
(12)

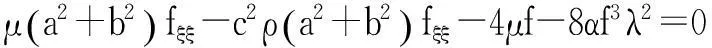
(13)

將式(12)關(guān)于ξ積分得

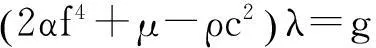
(14)

式中，g為積分常數(shù)。

將式(14)代入式(13)可得

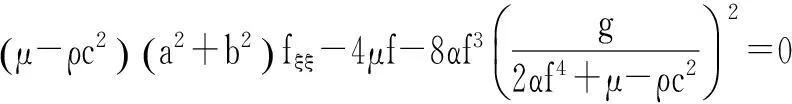
(15)

為研究方便，引入下列無量綱記號：

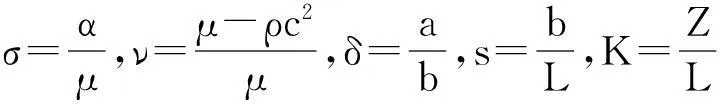
(16)

將式(16)代入式(15)可得

(17)

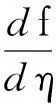
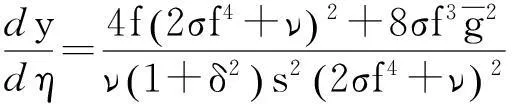
(18)

(19)

式中，h是積分常數(shù)。

根據(jù)式(19)可得

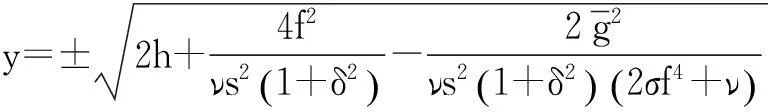
(20)

將式(20)代入式(18)的第一個方程得

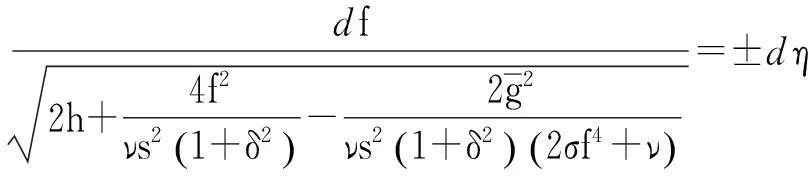
(21)

將式(21)兩邊同時積分得

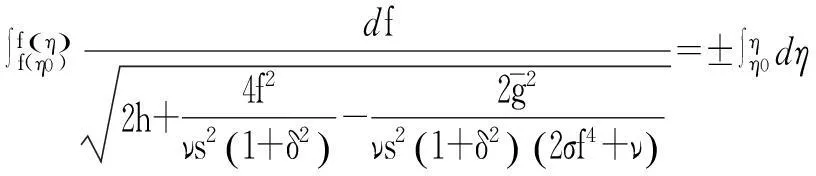
(22)

式(22)是徑向變形函數(shù)f關(guān)于變量η的隱式解析解。

根據(jù)式(14)得

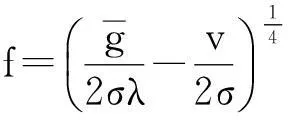
(23)

將式(23)代入式(22)得

(24)

(25)

式(25)是軸向伸長率λ關(guān)于變量η的隱式解析解。進而可以求得軸向變形函數(shù)z。

3結(jié)語

本文導(dǎo)出了一類可以用于描述各向同性近似可壓縮的超彈性圓柱管徑向和軸向?qū)ΨQ運動的非線性發(fā)展方程組。得到了圓柱管徑向變形和軸向伸長率的隱式解析解。在本文工作的基礎(chǔ)上，對于定解問題，還可以分析不同的初始條件、邊界條件和不同的積分常數(shù)以及不同的參數(shù)對隱式解析解的定性性質(zhì)的影響。

參考文獻：

[1]DAIHH,LIJ.NonlineartravellingwavesinahyperelasticrodcomposedofacompressibleMooney-Rivlinmaterial[J].InternationalJournalofNon-LinearMechanics, 2009, 44(5): 499-510.

[2]KNOWLESJK.Largeamplitudeoscillationsofatubeofincompressibleelasticmaterial[J].QuartApplMath, 1960, 18(1): 71-77.

[3]RENJ.Dynamicalresponseofhyper-elasticcylindricalshellsunderperiodicload[J].AppliedMathematicsandMechanics, 2008, 29: 1319-1327.

[4]YUANXG,ZHANGRJ,ZHANGHW.Controllabilityconditionsoffiniteoscillationsofhyper-elasticcylindricaltubescomposedofaclassofOgdenmaterialmodels[J].Computers,MaterialsandContinua, 2008, 7(3): 155-165.

[5]NIUD,YUANX,CHENGC,etal.Dynamiccharacteristicsinincompressiblehyperelasticcylindricalmembranes[J].ActaMechanicaSolidaSinica, 2010, 23(5): 420-427.

[6]COLEMANBD,NEWMANDC.Onwavesinslenderelasticrods[J].ArchiveforRationalMechanicsandAnalysis, 1990, 109(1): 39-61.

[7]DAIHH,ZHAOXH.NonlineartravellingwavesinarodcomposedofamodifiedMooney-Rivlinmaterial.I.Bifurcationofcriticalpointsandthenon-singularcase[C]//ProceedingsoftheRoyalSocietyofLondonA:Mathematical,PhysicalandEngineeringSciences.London:TheRoyalSociety, 1999, 455(1990): 3845-3874.

[8]COHENH,DAIHH.Nonlinearaxisymmetricwavesincompressiblehyperelasticrods:longfiniteamplitudewaves[J].ActaMechanica, 1993, 100(3-4): 223-239.

(責(zé)任編輯鄒永紅)

本文考慮如下的非線性發(fā)展方程組：

Implicit Analytical Solutions for a System of Nonlinear Evolution Equations

WANG Ran1, YUAN Xue-gang1, 2, ZHANG Hong-wu1, LV Na2

(1.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian Liaoning 116024, China ;2.School of Science, Dalian Minzu University, Dalian Liaoning 116605, China)

Abstract:This paper investigates the problem for solving a system of nonlinear evolution equations. The system can be used to describe the axisymmetric motion of a cylindrical tube composed of a class of isotropic approximate compressible neo-Hookean material models. Firstly, the system describing the radially symmetric and axisymmetric motion of the cylindrical tube is derived by the variational principle. Then the system can be reduced to a system of nonlinear ordinary differential equations by the traveling wave transformation. Finally, the first integral is obtained, and the implicit analytical solutions of the system of nonlinear evolution equations are given.

Key words:system of nonlinear evolution equations; hyperelastic cylindrical tube; nonlinear motion; implicit analytical solution

收稿日期：2015-11-16；最后修回日期：2015-11-20

基金項目：遼寧省教育廳高校優(yōu)秀人才支持計劃(LR2012044)；中央高校基本科研業(yè)務(wù)費專項資金資助項目(DC201502050203，DC201502050403)。

作者簡介：王然(1988-)，女，內(nèi)蒙古赤峰人，大連理工大學(xué)博士研究生，主要從事非線性動力學(xué)問題的解析解法和數(shù)值解法研究。通訊作者：袁學(xué)剛(1971-)，男，吉林樺甸人，教授，博士，學(xué)校優(yōu)秀學(xué)術(shù)帶頭人，博士生導(dǎo)師，主要從事非線性彈性材料和結(jié)構(gòu)的有限變形問題研究，E-mail:yxg1971@163.com。

文章編號：2096-1383(2016)03-0230-03

中圖分類號：O175;O343

文獻標志碼：A