基于關聯維指數分析的電力負荷預測算法

郭　崇，王　征

(1.遼寧工業大學 管理學院，遼寧 錦州　121001；2.國網遼寧省電力有限公司，沈陽　110006)

?

基于關聯維指數分析的電力負荷預測算法

郭崇1，王征2

(1.遼寧工業大學 管理學院，遼寧 錦州121001；2.國網遼寧省電力有限公司，沈陽110006)

摘要：電力負荷表現為一組非線性時間序列，通過對電力負荷的準確預測，避免電力負荷過載和用電集中擁堵，保障電網穩定可靠運行。傳統方法采用Lyapunove指數分岔預測算法，由于Lyapunove指數對電力負荷的初始狀態特征的敏感性，導致負荷采樣樣本較少時預測效果不好。提出一種基于關聯維指數分析的電力負荷預測算法，構建了電力負荷時間序列的信號模型，采用級聯FIR濾波器實現對電力負荷數據信息流的抗干擾濾波處理，進行信號提純，然后對電力負荷時域信號模型進行關聯維特征提取，采用關聯維特征在遞歸圖中的指數分岔性實現對負荷時間序列走勢的準確預測，實現電力負荷預測算法改進。仿真實驗結果表明，采用該算法進行電力負荷預測具有較好的預測準確性，指向性較好，且具有較好的抗干擾能力，在電力管理和調度中具有較好的應用性。

關鍵詞：關聯維；電力負荷；預測算法

電力網絡是保障人民生活和社會生產的基礎設施，需要對電力網絡中的負荷進行有效調度和管理，提高電力調度性能，保障電力系統管理的有效性和高效性。電力負荷是電力系統管理的一個重要指標，通過對電力負荷序列的分析，實現對電力系統的優化調度。在當前的電力系統和負荷預測管理中，存在著電力系統管理的浪費率居高不下的問題，從身邊的實際情況可以看出，不論是在核心的城市地區，還是在邊緣化地區，系統的電力浪費都是一個嚴重的問題。存在這一根本原因是對電力負荷的預測不夠準確，導致電力管理的時效性不好，為了避免電力負荷擁堵，提高電網運載的穩定性和可靠性，需要進行電力負荷的有效預測，提高預測精度，從而提高對電力負荷的宏觀調度和微觀管理能力，研究電力負荷的優化預測算法具有重要意義。

傳統方法中，對電力負荷的預測算法主要有基于粒子群算法的電力負荷預測算法、基于信號處理的電力負荷預測方法、基于專家系統識別的電力負荷預測算法和基于時頻分析的電力負荷預測算法等[1-3]，上述方法主要是將電力負荷當作一組線性時間序列。然后采用現代信號處理技術實現對負荷時間序列的信號重建和分析，實現電力負荷預測，當上述方法對電力負荷進行線性擬合過程中，在先驗知識缺乏時具有擬合精度不好的問題，影響了預測精度。對此，相關文獻進行了改進設計，其中，文獻[4]提出一種基于把粒子群算法引入到電力負荷預測和數據挖掘中，取得一定的預測效益，但算法對粒子群的趨同性導致對電力負荷預測的精度不好，且計算開銷較大；文獻[5] 提出一種基于粒子群退化重采樣的電力負荷解卷積測度提取方法，構建子圖模式庫，得到電力負荷序列的采集模型，對電力負荷進行合理分配，改善了預測精度，但是該方法無法對短時的電力負荷進行有效預測；文獻[6]通過計算最大Lyapunov指數，結合Wolf一步迭代預測算法實現對電力負荷預測，利用雙譜分析進行Lyapunov指數特征提取，在預測精度上有所改善，由于Lyapunove指數對電力負荷的初始狀態特征的敏感性，導致負荷采樣樣本較少時預測效果不好。

針對這些問題，本文提出一種基于關聯維指數分析的電力負荷預測算法。首先構建了電力負荷的信號模型，然后對電力負荷時域信號模型進行關聯維特征提取，以此為基礎采用關聯維特征在遞歸圖中的指數分岔性實現對負荷時間序列走勢的準確預測，仿真實驗進行了性能驗證，展示了本文算法在提高預測精度，改善電力負荷的調度和分配性能方面的優越性，得出有效性結論。

1電力負荷時間序列的信號模型構建和預處理

1.1信號模型構建

本文研究電力負荷預測算法，實現需要給出電力負荷時間序列的時域信號模型，采用信號處理方法實現對電力負荷的預測。進行電力負荷時間序列信息流預測模型構建中，首先進行電力負荷的調度模型分析，將待分析和預測的電力負荷數據按照五元組(srcIP、proto、dstIP、srcPort、dstPort)[7]，得到電力負荷的時間采樣和調度模型如圖1所示。

圖1　電力負荷的時間采樣和調度模型

電力負荷預測中，電力負荷時間序列在電力網絡中按照不同協議通信，在一段時間內上行電力負荷和下行電力負荷不等，采用粒子群優化算法實現對電力負荷模型構建，得到電力負荷序列的IP個數不確定系數為：

(1)

式中k——電力負荷數據的采樣時間間隔；n——粒子總數目。

通過對電力負荷的融合粒子群評價指導進行信號模型構建，設電力負荷時間序列信息流通信節點的采樣樣本A?V，B?V且A∩B=φ，采用利用時間窗口函數TW增加電力負荷預測中的相似用戶的數量，假設(F，Q)為多波束信息搜索的操作算子，在慣性系數布局中，采用混合差分粒子群調度，得到電力負荷的能量消耗：

Etotal=(α1+α2d1n0)+(β+α1+α2d2n0)

+…+(β+α1+α2dpn0)

(2)

(3)

電力負荷數據傳輸模型可以根據時間序列的狀態特征來描述，設時間窗口函數為Δw=wmax-wmin，則：

(4)

當d1=d2=…=dp時，電力負荷狀態空間中特征矢量的當前種群的迭代次數Etotal取最小值。當Etotal′=0，有最小值，此時，分布式干擾取得最小時，電力負荷的特征狀態空間的關聯維特征值函數為：

(5)

式中P——主頻特征；x(t)——原始電力負荷數據的長度；τ——時間尺度。

電力負荷時間序列信息流預測的每個傳輸調度集si(i=1，2，…，L)滿足以下條件：

(1)Si∩Sj=φ,?i≠j;

通過上述約束條件，得到一個高密度區域D，計算區域D內的電力負荷相空間，采用粒子群優化算法，計算粒子群差分擾動個體經歷過的最佳位置為pi=(pi1,pi2,……,piD)，采用Lagrange定理，求得電力負荷預測的目標函數的極值為：

(6)

(7)

式中xk——采樣時間序列；m——電力負荷時間序列信息流的嵌入維數；μik——電力負荷分岔的極大線性無關組。

通過上述分析，構建了電力負荷時間序列的信號模型為：

x(n)=s(n)+v(n)

(8)

式中s(n)——時頻信號；v(n)——電力網絡中的干擾噪聲分量；φi——電力負荷時間序列的非平穩態寬頻帶系數。

通過信號模型的構建，采用關聯維特征提取算法進行負荷預測。

1.2抗干擾濾波預處理

在信號模型構建的基礎上，為了實現對電力負荷時間序列的準確預測，還要進行抗干擾濾波預處理。提高信號的純度，采用級聯雙工FIR濾波算法進行抗干擾濾波[8]，本文設計的濾波器的結構模型如圖2所示。

圖2　電力負荷時間序列信息流的抗干擾濾波結構模型

對于采集的電力負荷時間序列信息流，輸入到濾波器中，輸出為一組寬頻帶回波信息，假設輸入電力負荷時間序列為u(n)，輸出為x(n)的去干擾的寬頻帶信號模型，結合濾波器的結構模型，得到電力負荷的其輸入與輸出的關系為：

(9)

為了反映電力負荷時間序列信息流的內部特征，進行級聯FIR濾波，得到濾波器的系統函數為：

(10)

式中電力負荷時間序列信息流盲分離的濾波器的級聯參數為ak，br為局部收斂權重，引入信號處理理論，假設電力負荷時間序列信息流通過數據預測分析，在t時刻的預測分析數據信息度為DCT(xt)=p(xt|d0，…，t)，得到電力負荷時間序列信息流的包絡特征為：

(11)

式中θ(t)——相位幅度值；a(t)——指向性包絡特征向量。

定義量度F(β，X)來評價由β=[β1，β2]所恢復的電力負荷時間序列信息流的y=βX的時間可預測性，利用瞬時頻率的概念將原電力負荷在x(t)的關聯信息特征為：

(12)

式中ai(t)——幅值；wi(t)——自適應加權。

通過以上處理，實現了電力負荷的抗干擾濾波，為進行電力負荷預測奠定基礎。

2關聯維指數特征分析和預測算法改進實現

在進行了電力負荷的信號模型構建和抗干擾濾波處理的基礎上，進行電力負荷預測算法改進設計，通過對電力負荷的準確預測，避免電力負荷過載和用電集中擁堵，保障電網穩定可靠運行。傳統方法采用Lyapunove指數分岔預測算法，由于Lyapunove指數對電力負荷的初始狀態特征的敏感性，導致負荷采樣樣本較少時預測效果不好。為了克服傳統方法的弊端，本文提出一種基于關聯維指數分析的電力負荷預測算法。采用自相關特征奇異分解對電力負荷序列進行線性特征疊加，得到電力負荷的關聯維指數的時間測度信息為：

(13)

|X(f)|2=TC2Nsinc2(πfTC)|Xcode(f)|2

(14)

(15)

式中TC——時域采樣閾值；f——頻率；|Xcode(f)|——信息加權特征向量。

則電力負荷時間序列信息流在重構的關聯指數測度空間中的特征分類集合為：Sl(nTB)=SQ(nTB)=±1，采用關聯維特征提取方法，設電力負荷的信號掃頻帶寬表示為：

(16)

(17)

z(t)=x(t)+iy(t)=a(t)eiθ(t)

(18)

式中a(t)——電力負荷預測數據點xi和xj之間的相異度；θ(t)——延遲時間互信息量。

根據合同變換矩陣，得到電力負荷預測的正定最小特征，得到協同過濾模糊概率時頻特征為：

ψ2(d2(t))=ψ+(h2-d2(t))L(Z2+Z3)-1LT

+d2(t)MT(Z2+Z3)-1MT

(19)

在Bochner-Riesz時頻空間中，定義第j類的電力負荷預測的輸出的分離系數C，當Ψ(d1(t)，d2(t))<0，有：

(20)

采用關聯維特征在遞歸圖中的指數分岔性實現對負荷時間序列走勢的準確預測，得到電力負荷時間序列信息流的預測值可以用下式描述為：

(21)

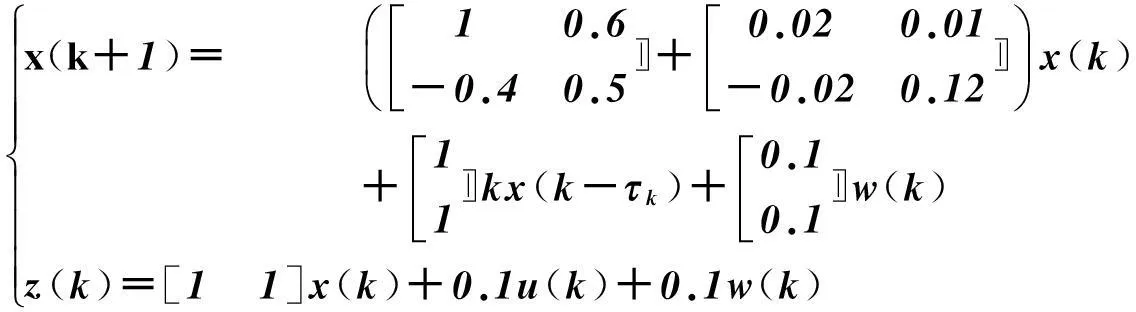
x(k+1)= 10.6-0.40.5é?êê?+0.020.01-0.020.12é?êê??è???÷x(k) +11é?êê?kx(k-τk)+0.10.1é?êê?w(k)z(k)=[1 1]x(k)+0.1u(k)+0.1w(k)ì?í???????

(22)

由此實現算法改進，下一步通過仿真實驗進行電力負荷預測性能測試與驗證。

3仿真實驗與性能驗證

為了測試本文算法在實現電力負荷預測中的性能，進行仿真實驗。仿真實驗的硬件環境描述如下：操作系統 Windows XP，編譯軟件Matlab7.0.1。首先進行電力負荷數據的采樣和先驗知識分析，電力負荷原始數據的采樣率為20 Kps/s，采集源于大型市電供電網絡的電力負荷時間序列信息，然后進行級聯FIR濾波器的設計，假設濾波器的級聯長度為L=25，粒子群數量M為300個，采樣頻率為f1=0.3，f2=0.05，信噪比SNR=-10～0 dB。根據上述仿真環境和參數設定，進行仿真實驗，首先給出電力負荷數據帶噪聲的信號的濾波輸出信號時域波形見圖3。

圖3　電力負荷數據的時域信號波形及濾波輸出

從圖3可見，采用本文方法進行電力負荷的時域波形采樣，能準確反映電力負荷的時域信息特征，通過本文設計的FIR濾波器進行信號濾波，提高了數據的純度，為電力負荷的準確預測奠定基礎。在此基礎上，進行電力負荷的關聯維指數特征提取的分析，采用關聯維特征在遞歸圖中的指數分岔性實現對負荷時間序列走勢的準確預測，得到輸出的電力負荷的關聯維指數譜見圖4。

圖4　電力負荷的關聯維指數分析及預測結果

從圖4可見，采用本文方法，通過關聯維指數分析，能有效分析出電力負荷的時域走勢，實現對電力負荷數據的準確預測，具有較好的預測準確性，指向性較好。為了定量分析和對比算法性能，采用本文方法和傳統方法，以預測精度為測試指標，得到結果如圖5所示。從圖5可見，采用本文算法進行電力負荷預測的精度較高。

圖5　預測準確度概率圖

4結語

通過對電力負荷的準確預測，避免電力負荷過載和用電集中擁堵，保障電網穩定可靠運行。本文提出一種基于關聯維指數分析的電力負荷預測算法。首先構建了電力負荷的信號模型，采用級聯FIR濾波器實現對電力負荷信號的濾波處理，實現信號提純，然后對電力負荷時域信號模型進行關聯維特征提取，以此為基礎采用關聯維特征在遞歸圖中的指數分岔性實現對負荷時間序列走勢的準確預測，實現電力負荷預測算法改進。研究結果表明，采用本文算法進行電力負荷預測的準確度較高，精度較好，且具有較好的抗干擾能力。研究成果將在電力調度和管理等方面都具有較好的應用價值。

參考文獻：

[1]蔣蕓,陳娜,明利特,等.基于Bagging的概率神經網絡集成分類算法[J].計算機科學,2013,40(5):242-246.

JIANG Yun, CHEN Na, MING Li-te, et al. Bagging-based probabilistic neural network ensemble classification algorithm[J]. Computer Science,2013,40(5):242-246.

[2]謝勝利，孫功憲，肖明，等．欠定和非完全稀疏性的盲信號提取[J]．電子學報，2010，38(5):1028-1031.

[3]JIANG Yi, ZHAO Hui. A new weak signal detection method based on stochastic resonance and array sensors[C].2013 International Conference on Communications,Circuits and Systems(ICCCAS),Chengdu,China,2013:287-289.

[4]CHEN Wei, WANG Jun, LI Hu-sheng,et al. Stochastic resonance noise enhanced spectrum sensing in cognitive radio networks[C].2010 IEEE Global Telecommunications Conference,Florida,USA,2010:1-6.

[5]WANG Jun, REN Xin, ZHANG Shao-wen,et al. Adaptive bistable stochastic resonance aided spectrum sensing[J].IEEE Transactions on Wireless Communications,2014,13(7):4014-4024.

[6]WEI Shi-peng,ZHANG Tian-qi,GAO Chun-xia,et al. The united detection of weak MSK signal using Duffing oscillator and Stochastic resonance[C].2011 IEEE 4th International Symposium on Microwave,Antenna,Propagation,and EMC Technologies for Wireless Communications(MAPE),Beijing,China,2011:447-453.

[7]朱文濤,蘇濤,楊濤,等.線性調頻連續波信號檢測與參數估計算法[J].電子與信息學報,2014,36(3):552-558.

[8]MENG Yun-liang, PEI Chang-xing.Stochastic resonance in a bistable system driven by non-gaussian noise and Gaussian noise[C].2014 IEEE Workshop on Electronics,Computer and Applications,Ottawa,Canada,2014:358-361.

(本文編輯：嚴加)

Power Load Prediction Algorithm Based on Correlation Dimension Index Analysis

GUO Chong1, WANG Zheng2

(1. Department of Management, Liaoning University of Technology, Jinzhou 121001, China;2. State Grid Liaoning Electric Power Company, Shenyang 110006, China)

Abstract:Power load performance is a set of nonlinear time series, whose accurate prediction can avoid power overload and consumption congestion and ensure the stable and reliable grid operation. The traditional Lyapunove exponent bifurcation prediction algorithm may produce poor forecasting result if the load samples are unsuffiecient because of the sensitivity of the initial state of the Lyapunove index to the initial state of the power load. This paper proposes a power load forecasting algorithm based on correlation dimension index analysis. The signal model of power load time series is constructed, and the FIR filter is used to realize the anti-interference filtering processing of power load data, and then the correlation dimension is extracted. The simulation results show that the proposed method has good accuracy in forecasting power load, good directivity, good anti-disturbance ability, and has good application in electric power management and scheduling.

Key words:correlation dimension; power load; forecasting algorithm

DOI：10.11973/dlyny201602011

作者簡介：郭崇(1980)，女，碩士，講師，研究方向為電子商務與數據挖掘。

中圖分類號：TP391

文獻標志碼：A

文章編號：2095-1256(2016)02-0202-05

收稿日期：2016-01-16