基于卡爾曼濾波的動(dòng)態(tài)定位優(yōu)化*

陳　剛　王　威　狄　鵬

(1.海軍工程大學(xué)管理工程系　武漢　430033)(2.海軍工程大學(xué)艦船工程系　武漢　430033)

?

基于卡爾曼濾波的動(dòng)態(tài)定位優(yōu)化*

陳剛1王威2狄鵬1

(1.海軍工程大學(xué)管理工程系武漢430033)(2.海軍工程大學(xué)艦船工程系武漢430033)

摘要針對(duì)動(dòng)態(tài)定位中存在很多隨機(jī)因素影響定位精度的問題，本文將卡爾曼濾波技術(shù)應(yīng)用于動(dòng)態(tài)定位中，設(shè)計(jì)出了卡爾曼濾波器，對(duì)隨機(jī)因素造成的誤差進(jìn)行濾波以減小定位誤差，提高了定位精度。卡爾曼濾波技術(shù)是一種線性最小方差濾波估計(jì)，它只需要通過上一時(shí)刻狀態(tài)向量的最優(yōu)估計(jì)和現(xiàn)在時(shí)刻的觀測量就可以得到現(xiàn)在時(shí)刻狀態(tài)向量的最優(yōu)估計(jì)值。論文首先以物體在二維空間運(yùn)動(dòng)為例，建立系統(tǒng)的狀態(tài)轉(zhuǎn)移方程以及測量方程，然后采用濾波器對(duì)測量值進(jìn)行濾波處理，最后采用算例進(jìn)行仿真。仿真結(jié)果表明,將卡爾曼濾波技術(shù)應(yīng)用于動(dòng)態(tài)定位中，能有效地優(yōu)化動(dòng)態(tài)定位，提高定位精度。

關(guān)鍵詞卡爾曼濾波; 動(dòng)態(tài)定位; 隨機(jī)因素; 狀態(tài); 最優(yōu)估計(jì)

Class NumberP228

1引言

如何獲得準(zhǔn)確的位置和時(shí)間信息對(duì)于目前的社會(huì)活動(dòng)極其重要，在實(shí)際動(dòng)態(tài)定位中，會(huì)存在很多隨機(jī)干擾因素影響定位的精度，例如使用GPS定位時(shí)，衛(wèi)星的星歷誤差、衛(wèi)星鐘差、多路徑效應(yīng)、接收機(jī)本身的噪聲、電離層及對(duì)流層等都會(huì)對(duì)定位產(chǎn)生干擾。隨著時(shí)代發(fā)展，定位技術(shù)也不斷成熟，傳輸時(shí)延差TDOA[1～4]、差分GPS[5～7]等定位技術(shù)使定位精度不斷提高，但因需要建立差分GPS基準(zhǔn)站以及受到差分GPS所面臨的信號(hào)作用范圍限制，在很多特殊場合滿足不了定位精度要求，迫切需要新的技術(shù)來提高定位精度。卡爾曼博士在1961年提出了一種線性濾波估計(jì)理論，即卡爾曼濾波[9～10]，這種濾波引入了控制理論狀態(tài)空間的概念，只需要通過上一時(shí)刻狀態(tài)向量的最優(yōu)估計(jì)和現(xiàn)在時(shí)刻的觀測量，然后在時(shí)域內(nèi)進(jìn)行線性遞推計(jì)算，就可將真實(shí)的狀態(tài)從各種干擾中實(shí)時(shí)最優(yōu)地估計(jì)出來。卡爾曼濾波已成功應(yīng)用于動(dòng)態(tài)數(shù)據(jù)處理[11]、慣性導(dǎo)航[12～14]中，使用卡爾曼濾波和其它算法相結(jié)合能有效地減少動(dòng)態(tài)定位中的誤差，提高定位的精度。

2卡爾曼濾波算法

卡爾曼濾波算法是一種遞推的線性最小方差估計(jì)方法，它通過建立狀態(tài)方程和量測方程來描述系統(tǒng)的動(dòng)態(tài)變化過程。由前一時(shí)刻的估計(jì)值和新獲得的觀測數(shù)據(jù)，依據(jù)濾波增益矩陣的變化，遞推計(jì)算出新的估計(jì)值，最后得到系統(tǒng)狀態(tài)的最優(yōu)估計(jì)。無需存儲(chǔ)不同時(shí)刻的觀測數(shù)據(jù)，便于實(shí)時(shí)數(shù)據(jù)處理。因此被廣泛應(yīng)用于船舶、雷達(dá)以及導(dǎo)航等動(dòng)態(tài)定位的數(shù)據(jù)處理中。

假設(shè)系統(tǒng)的狀態(tài)向量為X，觀測向量為Z，觀測向量Z可由狀態(tài)向量X進(jìn)行表示，觀測方程為

Z(k)=H(k)X(k)+V(k)

其中H(k)表示觀測矩陣，V(k)表示觀測的噪聲。

不考慮控制項(xiàng)，系統(tǒng)由k-1時(shí)刻狀態(tài)轉(zhuǎn)移k時(shí)刻狀態(tài)可由狀態(tài)轉(zhuǎn)移方程進(jìn)行表示:

X(k)=Φ(k|k-1)X(k)+W(k)

其中Φ(k|k-1)表示狀態(tài)轉(zhuǎn)移矩陣，W(k)表示系統(tǒng)過程的噪聲。

關(guān)于系統(tǒng)過程噪聲和觀測噪聲的統(tǒng)計(jì)特性，假定如下:

其中Qk是系統(tǒng)過程噪聲W(k)的非負(fù)定方差矩陣；Rk是系統(tǒng)觀測噪聲V(k)的正定方差矩陣，δkj是Kronecker-δ函數(shù)。

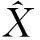
狀態(tài)一步預(yù)測

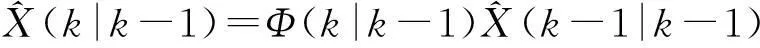
狀態(tài)估計(jì)

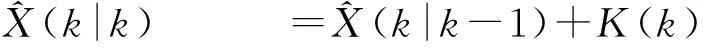
^X(k|k) =^X(k|k-1)+K(k)

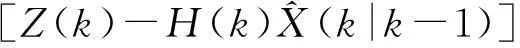
濾波增益矩陣

K(k)=P(k|k-1)H(k)T/H(k)P(k|k-1)H(k)T

一步預(yù)測誤差方差矩陣

P(k|k-1)=Φ(k|k-1)P(k-1|k-1)

Φ(k|k-1)T+Q(k)

估計(jì)誤差方差矩陣

P(k|k)=[1-K(k)H(k)]P(k|k-1)

上述方程即為線性離散系統(tǒng)卡爾曼濾波方程。

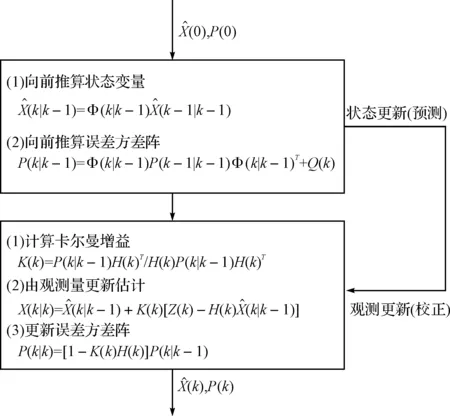
圖1　隨機(jī)線性離散系統(tǒng)卡爾曼濾波器流程圖

3卡爾曼濾波器模型的構(gòu)建

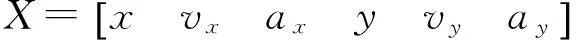
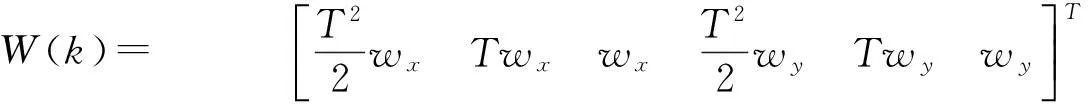
W(k)= T22wxTwxwxT22wyTwywyé?êêù?úúT

,

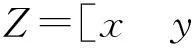
Z(k)=H(k)X(k)+V(k)

其中

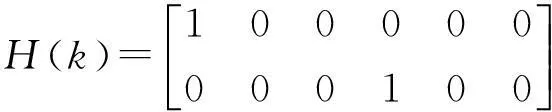
對(duì)于系統(tǒng)的過程噪聲wx、wy以及系統(tǒng)的測量噪聲v1、v2均為不相關(guān)的白噪聲過程， 其特性如下:

令系統(tǒng)過程噪聲方差矩陣為Q(k),系統(tǒng)測量噪聲方差矩陣為R(k)，可表示為

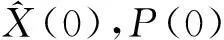
4仿真實(shí)驗(yàn)

為了驗(yàn)證所設(shè)計(jì)的卡爾曼濾波模型的可行性和有效性,進(jìn)行仿真試驗(yàn)。假設(shè)某物體沿x軸方向以速度vx0=5m/s的速度做勻速運(yùn)動(dòng)，沿y軸做初速度vy0=5m/s，ay=1m/s2的勻加速運(yùn)動(dòng)，采樣周期T=0.1s，采樣時(shí)間為10s。通過仿真模擬出測量噪聲為R(k)的觀測值Z(k)。設(shè)置相關(guān)仿真參數(shù)。

系統(tǒng)初始化位置及協(xié)方差矩陣為

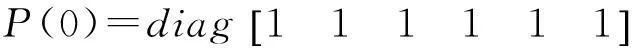
系統(tǒng)過程方差矩陣及測量方差矩陣

采用卡爾曼濾波器對(duì)系統(tǒng)觀測值Z(k)進(jìn)行濾波處理，濾波前后結(jié)果如圖2。

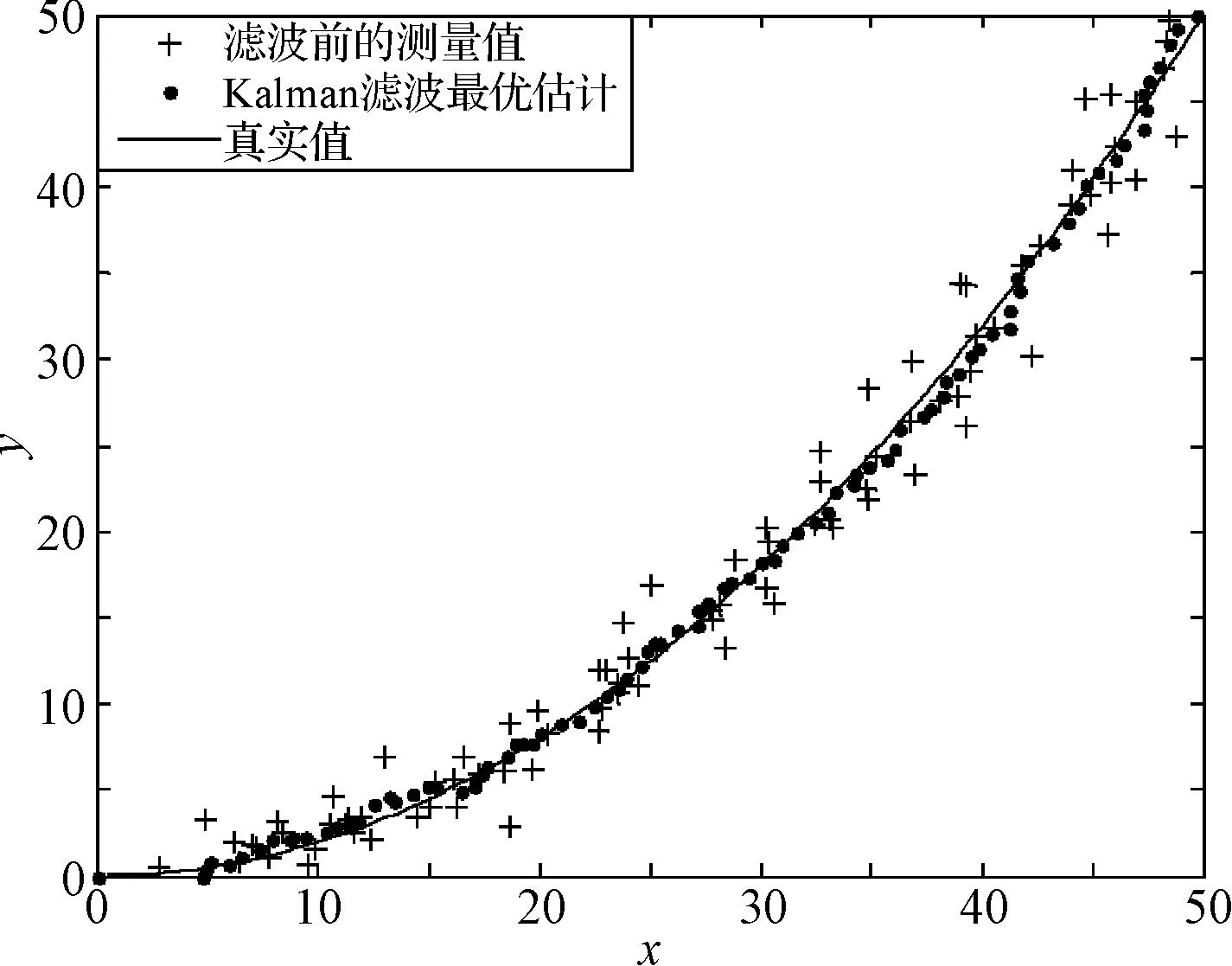
圖2　卡爾曼濾波結(jié)果

將最優(yōu)估計(jì)值、測量值與真實(shí)值進(jìn)行對(duì)比:

=370.04

=40.08

對(duì)濾波前后x軸，y軸方向做誤差分析如圖3和圖4。

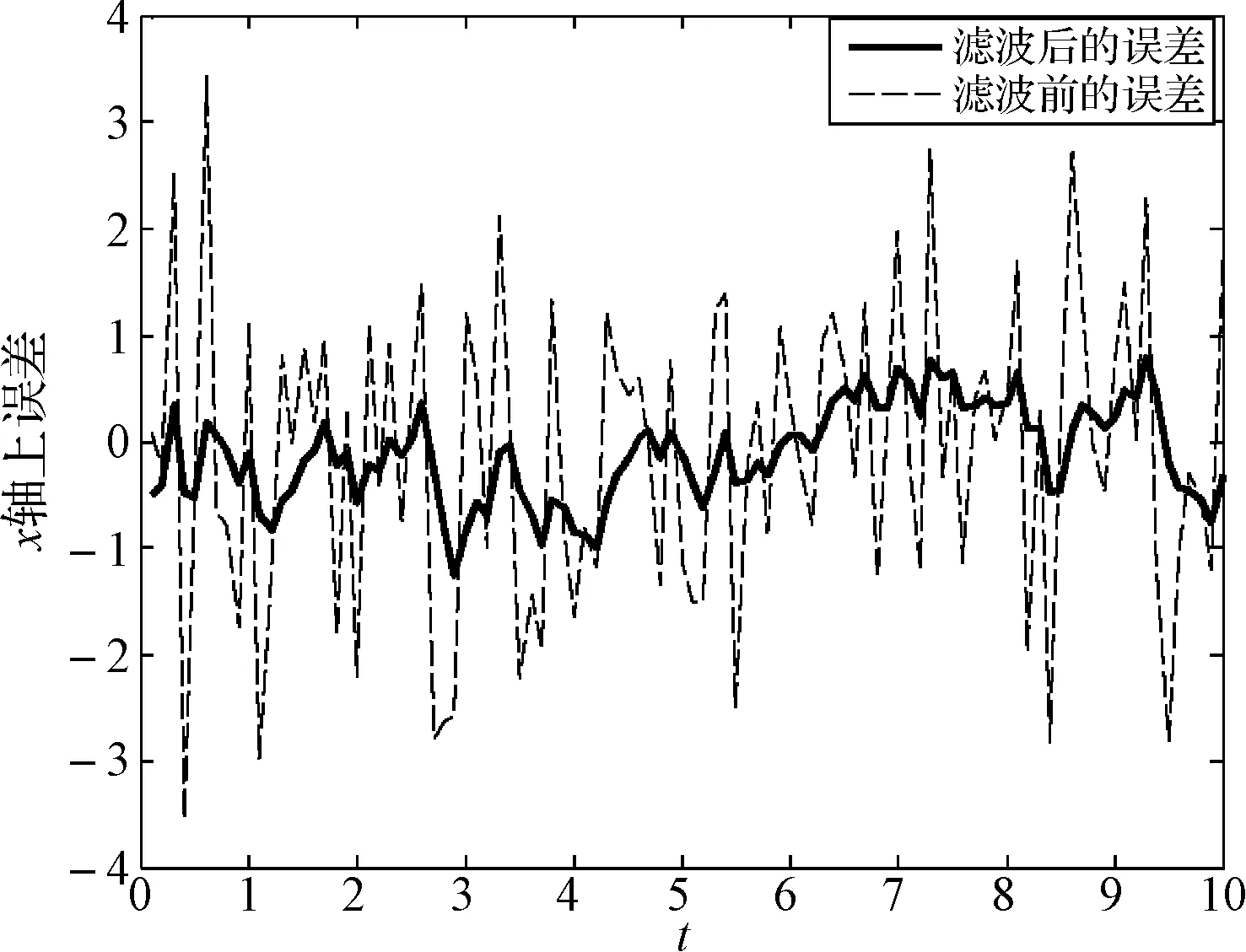
圖3　卡爾曼濾波前后x方向的誤差圖

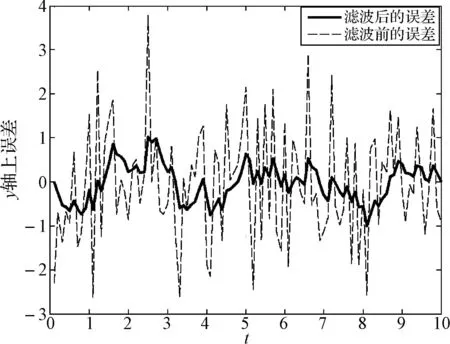
圖4　卡爾曼濾波前后y方向的誤差圖

可以看出測量值經(jīng)卡爾曼濾波器濾波后得到的最優(yōu)估計(jì)更加接近真實(shí)值，卡爾曼濾波器能更加有效地減小定位誤差。

5結(jié)語

通過建立系統(tǒng)運(yùn)動(dòng)的狀態(tài)轉(zhuǎn)移方程以及測量方程，采用卡爾曼濾波器對(duì)系統(tǒng)定位的測量值進(jìn)行優(yōu)化處理，得到系統(tǒng)狀態(tài)的最優(yōu)估計(jì)。最后的仿真算例結(jié)果表明，卡爾曼濾波在動(dòng)態(tài)濾波精度上有明顯改善，對(duì)動(dòng)態(tài)定位有明顯優(yōu)化效果，從而說明卡爾曼濾波算法具有一定的有效性和實(shí)用性。

參 考 文 獻(xiàn)

[1] 彭宇,王丹.無線傳感器網(wǎng)絡(luò)定位技術(shù)綜述[J].電子測量與儀器學(xué)報(bào),2011,25(5):389-396.

[2] 殷桂華,王小輝,雷毅談.基于TDOA的室內(nèi)運(yùn)動(dòng)目標(biāo)雙曲線RFID定位方法[J].計(jì)算機(jī)應(yīng)用,2014，34(S2):52-54.

[3] 劉華辰,劉麗莉,王奉章,等.基于TDOA測距模型的SOCP和Taylor混合定位方案[J].激光雜志,2015,32(2),107-112.

[4] 劉繼斌,劉培國,李高升,等.三維AOA /TDOA被動(dòng)定位及其迭代融合算法[J].全球定位系統(tǒng),2006(4):5-9.

[5] 張怡,張亮,廉保旺.差分GPS定位系統(tǒng)的衛(wèi)星位置算法研究[J].彈箭與制導(dǎo)學(xué)報(bào),2003(1):85-87.

[6] 牟聰,王偉,張明. 差分 GPS 應(yīng)用于機(jī)載雷達(dá)精度統(tǒng)計(jì)的方法研究火控雷達(dá)技術(shù)[J].2012(3):25-28.

[7] 楊世學(xué),劉宇明.高精度差分GPS技術(shù)在海洋資源調(diào)查中的應(yīng)用[J].南海地質(zhì)研究,2002:92-96.

[8] 王甫紅.高精度星載GPS實(shí)時(shí)定軌卡爾曼濾波模型[J].武漢大學(xué)學(xué)報(bào),2010(6):653-656.

[9] Kalman R.E.A new approach to linear filtering and Predietion Problem[J].Jornal of Basic Eng(ASME)，1960,82D:95-108.

[10] Jens G.Balchen,Nils A.Jenssen etc.A dynamic positioning system based on Kalman filtering and optimal contral[J].Identification and control,1980(3):135-163.

[11] 梁民贊,陸揚(yáng),周新鵬.一種抑制卡爾曼濾波發(fā)散的實(shí)時(shí)數(shù)據(jù)處理方法 [J].聲學(xué)技術(shù),2008(5):761-765.

[12] 戴革林,李珺.基于混合卡爾曼濾波的組合導(dǎo)航算法研究[J].網(wǎng)絡(luò)安全技術(shù)與應(yīng)用,2014(10):60-63.

[13] 崔平遠(yuǎn),鄭黎方,裴福俊,等.基于卡爾曼/粒子組合濾波器的組合導(dǎo)航方法研究[J].系統(tǒng)仿真學(xué)報(bào),2009(1):220-223.

[14] 劉愛元,戴洪德,盧建華,等.組合導(dǎo)航系統(tǒng)模擬器中的卡爾曼濾波設(shè)計(jì)[J].計(jì)算機(jī)與數(shù)字工程,2014(9):1649-1652.

Optimization of Dynamic Positioning Based on Kalman Filter

CHEN Gang1WANG Wei2DI Peng1

(1.Department of Management Science, Naval University of Engineering, Wuhan430033)(2.Department of Naval Architecture, Naval University of Engineering, Wuhan430033)

AbstractAiming at problems in the process of dynamic positioning，there are many random factors influencing positioning accuracy, Kalman filtering is applied to dynamic positioning, a Kalman filter is designed and the deviation caused by random factors is filtered to reduce the positioning deviation, the positioning accuracy is improved. Kalman filtering is one kind of linear minimum variance estimation methods. It can give the current optimal estimation of state vector with the current observation vector and the optimal estimation of last time. First, a model that objects move in the two-dimensional space is created and the transfer equation and measurement equation of the system state are given. And then the measured values is filtered. Last, the model is simulated. The results show that the Kalman filtering can effectively optimize the dynamic positioning, improve the positioning accuracy.

Key WordsKalman filter, dynamic positioning, random factors, state, optimal estimation

* 收稿日期：2015年11月11日,修回日期：2015年12月27日

作者簡介：陳剛，男，碩士，研究方向：系統(tǒng)管理。王威，男，博士，博士生導(dǎo)師，研究方向：系統(tǒng)工程。狄鵬，男，博士，碩士生導(dǎo)師，研究方向：裝備保障。

中圖分類號(hào)P228

DOI：10.3969/j.issn.1672-9730.2016.05.015