顆粒阻尼復合板結構振動響應預估

蘇俊收,耿彥波,高磊磊

(江蘇徐州工程機械研究院,江蘇,徐州,221004)

顆粒阻尼復合板結構振動響應預估

蘇俊收,耿彥波,高磊磊

(江蘇徐州工程機械研究院,江蘇,徐州,221004)

本文運用等效粘性阻尼模型,結合有限元軟件,對顆粒阻尼復合板的穩態振動響應進行了預估,并進行了相應的實驗驗證,得到的理論預估結果與實驗結果具有較好的一致性,說明等效黏性阻尼模型可以推廣應用到顆粒阻尼復合板結構振動響應預估中;之后,通過實驗分析了顆粒阻尼器不同布局、不同質量、不同顆粒對減振效果的影響,發現顆粒阻尼器阻尼特性表現出很大的差異,不僅各階振型表現不同,不同測量點也是差異很大,但總體上表現出了良好的寬頻減振特性,本文的研究為顆粒阻尼復合板結構的推廣應用奠定了基礎.

顆粒阻尼復合板; 等效黏性阻尼; 振動響應

顆粒阻尼技術具有減振頻帶寬、附加重量輕、適合于惡劣環境下工作等其他阻尼技術無可比擬的優點[1].工程車輛由于在野外作業,作業條件惡劣,自重噸位大、負荷變化頻繁的特點,自身振動較大.顆粒阻尼技術雖然在航空、汽車等領域已有了初步的發展[2][3][4],但在工程機械領域的研究卻很鮮見.隨著工程車輛作業條件更加復雜,減振要求更加迫切,輕量化趨勢日益推進,顆粒阻尼技術的優點變得更加突出,在工程機械行業中的應用前景更加巨大.

顆粒阻尼復合板結構是通過在結構體的內部加工適當大小和適當數量的孔洞或者在其上面安裝附屬裝置,并將顆粒體裝入其中的孔洞或附屬裝置內使之處于非阻塞的狀態.這樣當結構體振動時就會帶動其中的顆粒體振動,顆粒體與顆粒體相互之間以及顆粒與結構體之間的不斷碰撞、摩擦就會消耗掉結構體的振動,從而起到減振的作用.顆粒阻尼幾乎不受溫度限制,布置位置非常靈活,可以附加于工程車輛結構構件的外部,也可以內嵌于結構構件中,且在任意夾層、內部空洞均可置放,不影響結構使用,也不會增加較大重量.

由于顆粒阻尼減振機理較為復雜,目前仍沒有很好的理論來指導其應用,這在一定程度上影響了顆粒阻尼技術進一步的應用,西安交通大學的吳成軍教授開發出一種基于氣固兩相流理論的顆粒阻尼減振效果預估模型,并應用該模型進行顆粒阻尼懸臂梁的強迫振動響應預估與分析中,本文運用吳教授提出的等效黏性阻尼模型,對更為復雜的顆粒阻尼復合板結構進行研究,推進顆粒阻尼技術的進一步應用.

1 理論預估

本部分仿真用的板如圖1所示,板采用的材料為鋁合金,其密度為2 700 kg/m3,彈性模量為56 GPa;板的厚度為6 mm,夾持區域為60 mm×50 mm的長方體,懸空區域為300 mm×200 mm的長方體.顆粒阻尼器的腔體為直徑14 mm,高20 mm的圓柱體,其質量為11.45 g,填充顆粒為鎢粒,密度為17 000 kg/m3,平均粒徑為0.3 mm.阻尼器、激勵點以及測量點的位置如圖1所示.

圖1 顆粒阻尼板仿真示意圖Fig.1 Simulation diagram of particle-damping plate

仿真應用多物理場耦合軟件ANSYS以及MATLAB軟件進行計算.仿真前,先根據實際條件建立模型.通過實驗測量光板的加速度響應,應用半功率帶寬法求得結構的阻尼損耗因子為0.018.仿真時,根據實際條件施加相應的約束以及激勵.阻尼器的影響通過一個集中質量及集中力來模擬.集中質量等于阻尼器的質量,而集中力為一個隨著阻尼器施加點速度變化的量,其表達式集中力表達式為[5]:

式中m——系統的質量矩陣；

k——系統的剛度矩陣；

c——系統固有阻尼矩陣；

f——阻尼器的等效力矢量;

F——系統所施加的外力矢量.

由于該部分仿真進行的是諧響應分析,而上述集中力是一個隨著施加點速度變化的力,在ANSYS中進行諧響應分析時是不能直接施加這樣一個隨著時間變化的力的.通過分析,發現可以通過彈簧系統來施加該力,可以將彈簧的粘性力設為上述力表達式.這樣,我們就巧妙地實現了顆粒阻尼在板上的模擬.

仿真時夾持區域采用固定約束,在如圖1所示的三個位置施加顆粒阻尼器,阻尼器的質量填充比均設定為40%.計算在正弦激勵力的作用下,如圖所示的12個測量點的加速度響應.為對比方便,計算出各個測量點的加速度傳遞函數(加速度與激勵力的比值),圖2列出了未施加阻尼器以及施加阻尼器時板的其中幾個測量點的加速度傳遞函數.

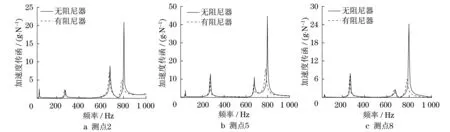
圖2 顆粒阻尼板的加速度傳遞函數Fig.2 Acceleration transfer function of particle-damping plate

從圖2中的仿真結果可以看出,施加顆粒阻尼器之后,板的加速度傳遞函數幅值有著較為明顯的降低,對于幾個測量點的各階峰值都有一定程度的降低,而第四階峰值的降低尤為明顯.

2 實驗驗證

為驗證理論預估結果的正確性,進行相應的實驗驗證,實驗裝置圖如圖3所示,實驗中的各參數與理論預估中相同.由于需要計算加速度響應的傳遞函數,本文同時測試測量點的加速度信號以及激勵點的激勵力信號.將測量到的數據與仿真結果放在一起對比,光板(未施加阻尼器)的加速度傳遞函數仿真結果及實驗結果對比如圖4所示,施加顆粒阻尼器的板的加速度傳遞函數仿真結果及實驗結果對比如圖5所示.

圖3 顆粒阻尼板實驗裝置圖Fig.3 Experimental apparatus diagram of particle-damping plate

圖4 光板(未施加阻尼器)的加速度傳遞函數Fig.4 Acceleration transfer function of plate without damper

圖4中,本文列出了光板部分測量點的加速度傳遞函數的仿真結果與實驗結果對比.從中可以看出,光板的仿真結果與實驗結果有著較好的吻合度,在第二階振型峰值處兩者基本完全重合,但在第四階固有頻率處誤差較大.通過該結果對比,我們可以證明光板的仿真結果是正確的,可以以此參數設置進行顆粒阻尼板的仿真.

圖5 顆粒阻尼板的加速度傳遞函數結果對比Fig.5 Comparison of acceleration transfer function of plate without damper

在圖5中,列出了在板上施加質量填充比為40%的顆粒阻尼器時,板的部分測量點的加速度傳遞函數仿真結果與實驗結果對比.從圖中可以看出,仿真結果與實驗結果一致性較好,在很多區域內基本重合.這證明本文仿真是非常成功的,同時也說明本文對于顆粒阻尼的模擬是正確的.對于顆粒阻尼板,我們可以較好地預估其振動響應.

3 參數影響

3.1 不同阻尼器布局對減振效果的影響

通過實驗研究了顆粒阻尼器的施加位置組合對板的減振效果的影響,同樣使用三個阻尼器(固定質量填充比為40%),選取12個測點.阻尼器的布局變化如圖6所示(布局一的示意圖如圖1),同時測出測量點的加速度響應以及激勵點的激勵力,列出幾個測量點的加速度傳遞函數如圖7所示.

從圖 7可以看出,顆粒阻尼器的布局形式會嚴重影響其減振效果.總體而言,基本上是在二階共振峰值處,布局四減振效果最好;在三階共振峰值處,布局三減振效果最好;在四階共振峰值處,布局五減振效果最好.這樣的結果主要是由于阻尼器的布局位置剛好接近該階模態振型的峰值位置而導致的.這就告訴我們,若需要主要降低某階頻率的峰值時,在其振型峰值處布置阻尼器,可以達到較好的效果.另外,我們還可以發現,減振效果越好,其共振峰位置偏離光板固有頻率就越嚴重.這是由于當取得較好的減振效果時,阻尼器的振動幅度相對較小,顆粒基本停在阻尼器上,因此,顆粒對系統固有頻率影響就越小,偏離光板固有頻率就越大.

圖6 阻尼器布局圖Fig.6 Layout diagram of damper

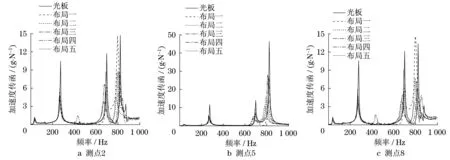
圖7 顆粒阻尼板的加速度傳遞函數(阻尼器布局影響)Fig.7 Acceleration transfer function of particle-damping plate(damper layout influence)

3.2 阻尼器、質量塊減振效果對比

通過實驗研究了顆粒阻尼器以及質量塊對板的振動的影響,同樣選用三個阻尼器(填充顆粒為鎢粉),同時選取三個質量塊進行試驗.三個質量塊的質量分別為:26.37 g(1號),25.47 g(2號),24.59 g(3號),填充顆粒使得三個阻尼器的質量與三個質量塊一致,阻尼器(或質量塊)以及測量點的布置如圖1所示,其中3號阻尼器(或質量塊)位于中間處,列出幾個測量點的加速度傳遞函數如圖8所示.

從上述測量結果可以看出,除個別測量點的某些頻率處(測點10的1 100 Hz左右),外,顆粒阻尼器都取得了較好的減振效果,基本上在每個峰值頻率處減振效果都較好.這說明顆粒阻尼器減振的寬頻特性.而只加質量塊則基本沒有降低峰值(在某些頻率處降低,而在某些頻率處升高);另外,還可以看出,雖然阻尼器的質量和質量塊相同,但施加阻尼器的板的各階固有頻率比添加質量塊的較高一點.

3.3 不同類型顆粒對減振效果的影響

通過實驗研究了顆粒材料對于顆粒阻尼器的減振效果的影響.這里,同樣使用三個阻尼器(固定質量填充比為40%),選取12個測點,阻尼器以及測量點的布置如圖1所示.分別選取0.3 mm的白剛玉、鐵粉和鎢粉進行實驗.三種材料如圖9所示,列出幾個測量點的加速度傳遞函數如圖10所示.

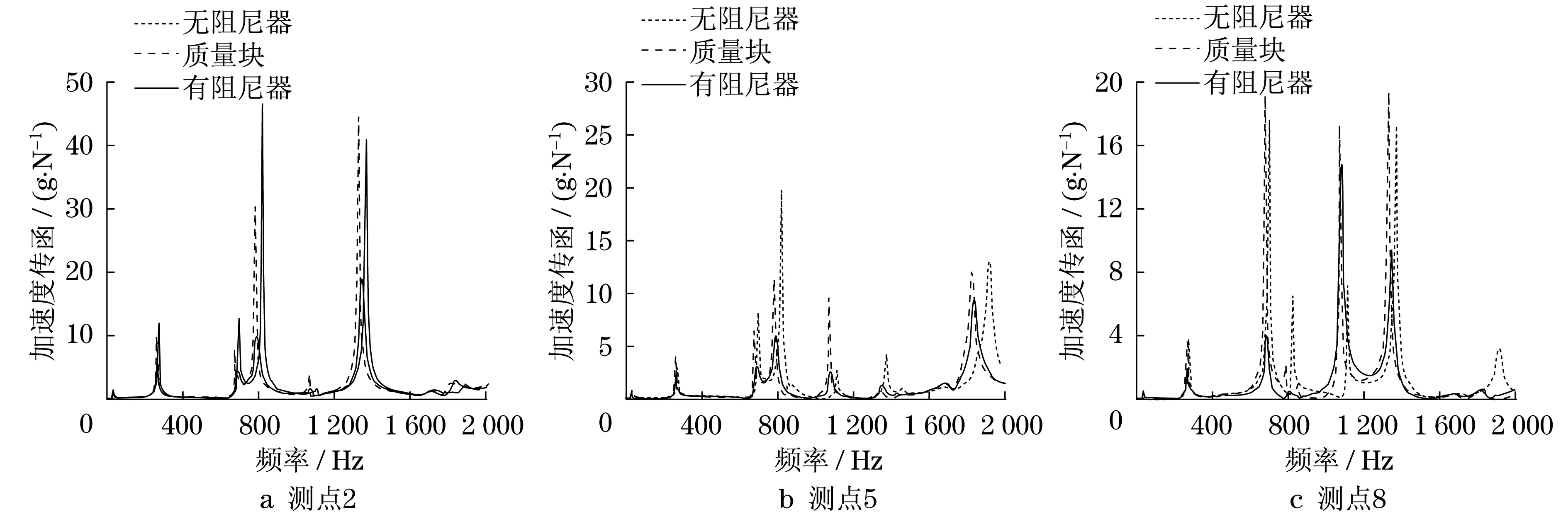
圖8 顆粒阻尼板的加速度傳遞函數(減振效果)Fig.8 Acceleration transfer function of particle-damping plate(vibration damping influence)

圖9 顆粒阻尼材料Fig.9 Particle-damping material

圖10中列出的為3號、4號和8號測量點的加速度傳遞函數響應.從圖中可以很明顯的看出,鎢粉的減振效果最好,鐵粉次之,而白剛玉最差.這是因為在材料密度方面,也是鎢粉最大,鐵粉次之,而白剛玉最小.因此,固定填充比時,鎢粉填充質量最大,所以取得最好的減振效果.另外,在不同測點體現出的效果也不同,如鎢粉在測點8的第四階峰值處減振效果非常好,而在測點3的第四階峰值處的減振效果比另外兩者還差.

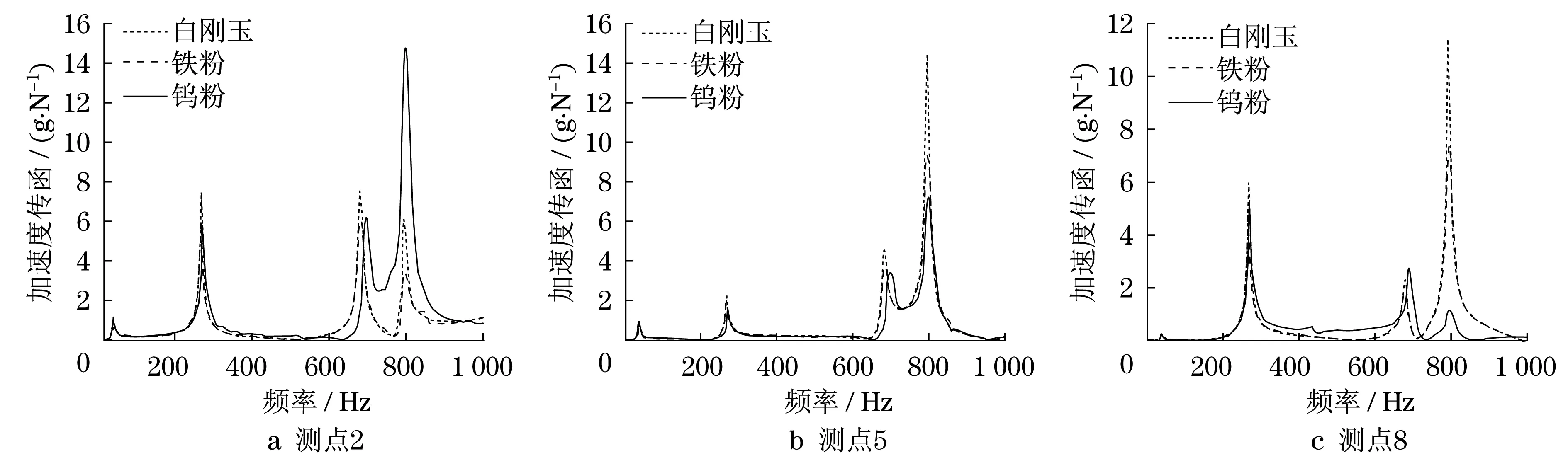
圖10 顆粒阻尼板的加速度傳遞函數(顆粒材料影響)Fig.10 Acceleration transfer function of particle-damping plate(particle-damping material influence)

4 結論

本文以氣固兩相流理論的顆粒阻尼減振效果預估模型為基礎,結合多物理場耦合軟件ANSYS對顆粒阻尼復合板的穩態振動響應進行了預估.得到的理論預估結果與實驗結果一致性較好,說明本文所運用的模型對顆粒阻尼復合板的振動響應的預估是成功的,這為顆粒阻尼復合板的進一步擴展應用奠定了基礎.本文在顆粒阻尼復合板的理論預估及實驗的過程中,發現顆粒阻尼器對板的減振效果表現出很大的差異性,不僅各階振型表現不同,不同測量點也是差異很大,但總體上表現出了良好的寬頻減振特性.

[1] 吳成軍.工程振動與控制[M].西安:西安交通大學出版社,2008.

WU Chengjun.Engineering vibration and control[M].Xi′an:Xi′an Jiao Tong University Publishers,2008.

[2] 申智春.顆粒阻尼在航天器減振中的應用與前景[J].應用力學學報,2011,28(6):608-612.

SHEN Zhichun.Application of particle damping in spacecraft vibration suppression[J].Chinese Journal of Applied Mechanics,2011,28(6):608-612.

[3] 夏兆旺,魏守貝.顆粒阻尼技術在制動鼓減振方面的應用研究[J].振動工程學報,2010,27(6):893-899.

XIA Zhaowang,WEI Shoubei,WEN Huabing.Application of particle damping in vibration attenuation of brake drum[J].Journal of Vibration Engineering,2010,27(6):893-899.

[4] 吳成軍,楊瑞超,王東強.基于氣體-顆粒兩相流理論的顆粒阻尼懸臂梁振動響應預估[J].機械工程學報,2013,49(10):53-61.

WU Chengjun,YANG Ruichao,WANG Dongqiang.Prediction on vibration response of cantilever particle-damping beam based on two-phase flow theory of gas-particle[J].Journal of Mechanical Engineering,2013,49(10):53-61.

[5] 閆維明,黃韻文.顆粒阻尼技術及其在土木工程中的應用展望[J].世界地震工程,2010,26(4):18-24.

YAN Weiming,HUANG Yunwen,HE Haoxiang.Particle damping technology and its application prospect in civil engineering[J].World Earthquake Engineering,2010,26(4):18-24.

[6] 倪振華.振動力學[M].西安:西安交通大學出版社.2005.

NI Zhenhua.Vibration mechanics[M].Xi′an:Xi′an Jiao Tong University Publishers,2005.

Pre-assessment on vibration responses from multiplex particle-damping plates

SU Jun-shou,GENG Yan-bo,GAO Lei-lei

(Jiangsu Xuzhou Construction Machinery Research Institute XCMG,Xuzhou 221004,China)

Based on previous works, an improved analytical model for equivalent viscous damping is first proposed. Then, the forced responses from a particle-damping plate is pre-assessed using the improved model and finite element method. Accordingly, the theoretical results are coincided with experimental ones. Finally, it is found that this model can rapidly and efficiently estimate vibration responses from particle-damping plates. Furthermore, the combination of three dampers in terms of different positions, masses and filling ratios is analyzed via testing with different damping properties, such as vibration modes and responses from measuring points. Nevertheless, good broadband vibration characteristics are generally detected. Therein, this approach is significant on practicality for particle-damping plates.

multiplex particle-damping plate; equivalent viscous damping; vibration response

蘇俊收(1988-),男,碩士,工程師.E-mail:sujunshou@163.com

U 463.1

A

1672-5581(2016)06-0493-06