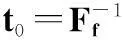融合外場使用和加速壽命數據的可靠性評估方法

蔡忠義, 陳云翔, 王莉莉, 羅承昆

(空軍工程大學裝備管理與安全工程學院, 陜西 西安 710051)

?

融合外場使用和加速壽命數據的可靠性評估方法

蔡忠義, 陳云翔, 王莉莉, 羅承昆

(空軍工程大學裝備管理與安全工程學院, 陜西 西安 710051)

摘要：針對壽命服從雙參數Weibull分布且已在外場使用一段時間后的機電產品,進行單應力、定時轉換的步進加速壽命試驗,研究外場使用數據和加速壽命試驗數據之間的融合評估問題。考慮到外場多應力環境與實驗室單一應力環境之間的差異性,構建基于修正系數的分布參數計算模型;開展融合外場使用歷程和加速壽命試驗過程的統計分析,建立各應力下的累計分布函數關系;構建融合過程的極大似然函數,運用數值迭代法,求解未知參數估計;結合某型機電產品進行仿真方案設計,采用蒙特卡羅仿真方法產生樣本數據,通過對比分析說明本文所提出的模型評估精度更高。

關鍵詞：加速壽命試驗; 可靠性評估; 應力環境差異; 修正系數; 數據融合

0引言

隨著科學技術的快速發展,機電產品的壽命與可靠性得以大幅提高并廣泛應用于航空航天、機械重工、電氣工程等領域。為了高效準確地評估機電產品的壽命與可靠性,在有限的試驗樣本和試驗經費的基礎上,需要采用加速壽命試驗,以達到評估產品可靠性的目的[1]。

針對機電產品加速壽命試驗數據的可靠性評估研究,一般思路為:假定產品壽命服從特定的分布模型(如Weibull),采用已知的加速模型,建立可靠性模型及似然估計函數,求解未知分布參數,從而外推出產品的壽命與可靠性[2-3]。目前,該領域的研究可歸納為以下:

一是應力施加方式。常見的有恒定、步進應力[4-5]。恒定應力試驗設計相對簡單,但所需的試驗樣本量較大;步進應力試驗因其可以充分利用試驗樣本信息,節約試驗時間和經費,在工程實踐中得以廣泛使用。就機電產品而言,步進應力加速壽命試驗主要適用于高可靠長壽命、價格昂貴、技術工藝上延續前批次且不影響系統安全的產品,以確保試驗風險在可控范圍內。如:針對軍用運輸機上的起動發電機,采用步進加速壽命試驗技術,開展了產品定延壽研究,為延長產品大修間隔期提供了技術支撐。

二是考慮外、內場環境差異性[6-9]。這類研究采用廣義加速模型,對外場多應力進行近似折算,從總體上對分布模型參數進行修正。如:文獻[8-9]在產品壽命服從Weibull場合下,針對恒定應力加速壽命試驗開展研究,考慮到外場應力與試驗應力之間的差異以及外場環境的復雜性,分別建立了考慮修正系數的加速模型和分布參數模型,從而外推出產品在外場使用環境下的壽命與可靠性。

三是融合多源壽命信息[10-13]。這類研究主要是采用數值迭代法或貝葉斯法來融合多源信息,建立未知分布參數的估計模型。文獻[10]采用Newton-Raphson迭代法求得壽命參數的極大似然估計,這種方法利用似然估計函數自身的收斂性來近似求解未知參數,易于理解,工程應用廣泛;文獻[12]綜合利用加速退化試驗信息、加速壽命試驗信息和外場信息,采用馬爾可夫蒙特卡羅(Markov Chain Monte Carlo, MCMC)方法,通過判斷馬爾可夫鏈的收斂性來求解未知參數的估計值,從而外推出產品外場壽命與可靠性。這種方法的優點是可以快速完成傳統似然函數的復雜求解過程,但對于未知參數先驗分布的選取還需進一步探討。

因此,本文針對壽命服從雙參數Weibull分布且在外場已使用一段時間的機電產品進行單應力、定時轉換的SSALT,建立考慮外場應力與環境差異的壽命分布修正模型,提出了融合外場使用和加速壽命數據的可靠性評估方法,采用數值迭代法來求解未知參數估計。

1考慮外場應力差異的壽命模型

1.1壽命模型

對于機電產品而言,一般認為其壽命服從Weibull分布,則Weibull場合下的產品壽命分布函數可表示為

(1)

式中,m為形狀參數;η為尺度參數;γ為位置參數。

當γ=0時,稱為雙參數Weibull,此時分布密度函數和可靠度函數分別為

(2)

(3)

1.2加速模型

加速模型是指在加速試驗中產品壽命特征量(如特征壽命、失效率等)與所施加的加速應力之間的關系模型,其中較為常見的是針對溫度應力的Arrhenius模型和針對電應力的逆冪律模型[14]。

對于雙參數Weibull,一般認為形狀參數m與應力S無關,而尺度系數η與應力S有關,用特征壽命tη=η(即R(tη)=e-1)作為加速模型的特征量,則加速模型可表示為

(4)

式中,a,b是待定常數;對于Arrhenius模型,φ(S)=1/S;對于逆冪律模型,φ(S)=lnS。

1.3考慮外場應力差異的模型修正

與內場(實驗室)應力環境相比,產品在外場工作環境所發生的失效機理更加復雜,通常是由多方面應力共同作用而出現的。因此,對于外場工作環境中的產品壽命分布模型應進行一定的修正。

若產品在外場工作環境中受諸如溫度、電壓、振動、濕度等多類型應力S,ST,SV,SM,…作用且僅有單一應力S被施加于ALT中,則基于ALT應力的加速模型可表示為

(5)

而基于外場使用環境下的多類型應力的廣義加速模型可近似表示為

(6)

式中,ηf和η分別為外場工作應力和ALT單一應力下的Weibull尺度參數。

若用ln(k1)(k1為應力修正系數)來代表除S以外的其他應力的影響,即

(7)

則由式(5)～式(7)可得

(8)

則有

(9)

雖然Weibull形狀參數m與應力無關,但考慮到產品組裝、工藝、維護保養、管理等因素的影響,外場使用中的產品與ALT中的產品會一定差異,用環境差異系數k2來表示這種差異,即

mf=m·k2

(10)

式中,mf和m分別為外場多應力和ALT單一應力下的Weibull形狀參數。

2融合外場使用和ALT的統計分析

2.1統計假設

對于開展融合外場使用數據和ALT數據統計的產品應滿足以下假設:

(1)ALT采用定時截尾方式,以溫度為步進試驗應力,各溫度Si(i=1,2,…,n)下產品壽命t之間相互獨立且都服從于雙參數Weibull(mi,ηi);

(2)ALT中產品失效機理保持不變,即各溫度Si下Weibull的形狀參數不變,令mi=m;

(3)ALT中產品滿足Nelson提出的累積失效模型,即產品的剩余壽命僅與當前應力和已累計失效水平有關;

(4)ALT各溫度Si下Weibull的特征壽命tηi=ηi與其溫度之間滿足以下加速方程:

(11)

2.2統計過程及數據

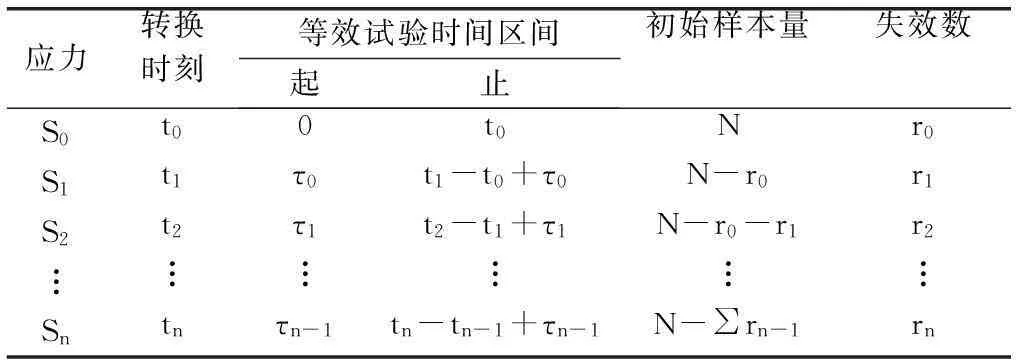
根據步進試驗方案,預先確定一組高于外場正常工作溫度S0的溫度應力S1

假設有一批共N個產品作為樣本總體,在進行SSALT前,該批產品已在外場工作了t0時刻且有r0個產品失效并記錄了失效時間,可近似看作是SSALT的第一步;然后將余下未失效產品放置在溫度應力S1下進行試驗,到達轉換時刻t1前有r1個產品失效并記錄了失效時間;而后將應力提高至S2繼續試驗,達到轉換時刻t2有r2個產品失效并記錄了失效時間;而后將應力提高至下一應力,如此進行,一直到將應力提高至Sn下截止tn時刻完成試驗(見圖1)。

圖1　考慮外場使用的步進應力施加過程

通過收集到上述整個過程的失效數據可知,各應力下的失效樣本時間序列如下:

獲取各應力下的數據樣本后,需要進行分布檢驗以判斷產品是否服從Weibull分布,一般采用F檢驗法、χ2檢驗法[15]。

2.3各應力下分布函數關系

已知N個產品在外場工作溫度為S0下的工作時間為t0,則t0時刻的產品累計失效概率為F0(t0),相當于產品在應力S1下τ0時刻的累積失效概率F1(τ0),則考慮了外場工作歷程的未失效產品在應力S1下進行試驗的起止時刻為(τ0,t1-t0+τ0]。

同理,產品在應力S1下t1-t0+τ0時刻的累計失效概率為F1(t1-t0+τ0),相當于在應力S2下τ1時刻的累積失效概率F2(τ1),則未失效產品在應力S2下進行試驗的起止時刻為(τ1,t2-t1+τ1]。依此遞推(見表1),可建立各應力下的壽命分布函數關系,則融合了外場使用和ALT數據的累計分布函數可分步表示如下:

步驟 1外場環境下溫度應力S0

(12)

式中,考慮到外場應力修正與環境差異系數,可知

(13)

式中,m0,η0為ALT應力S0下Weibull的形狀參數和位置參數。

步驟 2ALT溫度應力S1

(14)

式中,τ0可通過下式求出。

(15)

步驟 3ALT溫度應力S2

(16)

式中,τ1可通過下式求出。

(17)

步驟 i+1ALT溫度應力Si,i=1,2,…,n

(18)

式中,τi-1可通過下式求出。

(19)

3壽命可靠性模型

根據融合外場使用和ALT的統計過程分析及各應力的累積分布函數關系,建立整個融合過程的極大似然函數。

(1) 外場溫度應力S0下壽命數據極大似然函數為

(20)

(21)

(2)ALT各溫度應力Si下壽命數據極大似然函數為

(22)

(23)

其中

(24)

(3) 融合了外場和ALT數據的產品對數似然函數可表示為

(25)

(26)

4仿真實例

某型起動發電機是安裝在軍用飛機上為APU提供直流電源的供電裝置,屬于典型的機電產品。該型產品在部隊外場已使用一段時間,外場使用與維護數據充足,現需要綜合利用外場使用數據和ALT數據以推斷出其在外場正常使用下的壽命與可靠度。

4.1仿真數據

利用蒙特卡羅仿真方法產生整個融合過程的樣本數據[8],具體步驟如下:

步驟 2首先分別產生Ni(i=0,1,2)個相互獨立且服從于U[0,1]的隨機數;然后將其分為[0,p0)、[p0,p1)、[p1,p2)、[p2,1] 4組,分別對應于外場使用環境中樣本的失效概率,ALT中加速應力S1下樣本的失效概率,ALT中加速應力S2下樣本的失效概率以及到截尾時樣本仍未失效的概率。

步驟 3將產生的N0個隨機數中落入[0,p0)內的r0個隨機數U0j(j=1,2,…,r0)轉換為外場使用環境下的失效樣本時間為

(27)

步驟 4將產生的N1個隨機數中落入[p0,p1)內的r1個隨機數U1j(j=1,2,…,r1)轉換為ALT中加速應力S1下失效樣本時間為

(28)

步驟 5將產生的N2個隨機數中落入[p1,p2)內的r2個隨機數U2j(j=1,2,…,r2)轉換為ALT中加速應力S2下失效樣本時間為

(29)

4.2仿真方案

通過統計分析該機電產品或其同類產品在研制階段所進行的壽命試驗數據,結合經驗做法,可初步推斷出其壽命服從Weibull的參數值以及加速模型的參數值并作為仿真初值。具體仿真參數設置如下:

(1) 外場使用:外場應力與環境修正系數分別為k1=0.9,k2=1.1,初始樣本量N=20,正常工作溫度S0為50oC,p0=0.1;

(2)ALT:加速應力數為2,即S1=75oC、S2=100oC,p1,p2分別取0.3、0.7;

(3) 加速模型:Arrhenius模型參數a、b分別為9.174、-2.248,分布模型的形狀參數m=2.168;

(4) 仿真次數M=100。

4.3對比分析

根據上述仿真方案所產生的外場使用與ALT樣本數據,將本文所提出的融合外場使用和ALT數據且考慮了外場應力與環境差異的方法記為M1,將融合外場使用和ALT數據但未考慮外場應力與環境差異的方法記為M2,將只利用ALT數據進行評估的方法記為M3,分別推斷出產品壽命指標,通過對比分析來判斷各方法的擬合精度。

(1) 判斷標準

依據赤池信息量準則(Akaikeinformationcriterion,AIC)和總體均方誤差(totalmeansquarederror,TMSE)來判斷方法的優劣[9],計算公式為

AIC=2p-2lnL(Θ)

(30)

式中,p為Θ中未知參數的個數;lnL(Θ)為對數似然函數所取的極大值。

(31)

(2) 參數估計

采用Newton-Raphson迭代法對式(26)進行尋優,求解不同方法下的參數估計值;根據式(30)、式(31),計算出各方法的AIC和TMSE(見表2)。由表2可知,各模型擬合的優劣程度依次為:M1優于M2,M2優于M3。

表2　不同方法的參數估計結果

(3) 評估結果

根據式(26),計算出產品在外場正常使用下的特征壽命估計值,從而繪制出各方法所得到的產品可靠度曲線(見圖2)。從圖中可直觀看出,本文所提出的考慮了外場差異且融合了外場使用和ALT數據的評估模型精度最高,具有良好的趨勢擬合性;而傳統未考慮外場差異且只利用ALT數據的評估模型精度最差,主要是因其將參與ALT的樣本都視為新品,忽略了外場工作歷程會降低產品可靠度。

圖2　不同方法的可靠度曲線

5結論

(1) 針對具有外場工作歷程且壽命服從雙參數Weibull的機電產品,開展SSALT,提出了融合外場使用和ALT數據的可靠性建模方法;

(2) 考慮了外場應力環境的差異,采用雙修正系數,對外場正常工作應力下的Weibull分布參數進行修正,使得分布模型更加符合外場實際;

(3) 本文從修正壽命分布模型和擴大樣本量兩方面著手,所提出的方法能較好地反映產品壽命特征規律。通過與傳統未考慮外場差異和未融合外場數據的模型評估結果比較,進一步說明本方法較傳統方法的評估精度更優,具有良好的工程應用價值。

參考文獻：

[1] Zhang C H, Wen X S, Chen X. A comprehensive review of accelerated life testing[J].ActaArmanentarii, 2004, 25(4): 485-490. (張春華, 溫熙森, 陳循. 加速壽命試驗技術綜述[J].兵工學報, 2004, 25(4): 485-490.)

[2] Ding C, Yang C Y, Tse S K. Accelerated life test sampling plans for the Weibull distribution under Type I progressive interval censoring with random removals[J].JournalofStatisticalComputationandSimulation, 2010, 80(8): 903-914.

[3] Zhang X P, Shang J Z, Chen Xun, et al. Statistical inference of accelerated life test with competing failures based on three-parameter weibull distribution[J].ActaArmanentarii, 2013, 34(12): 1603-1610. (張詳坡, 尚建忠, 陳循, 等. 三參數Weibull分布競爭失效場合加速壽命試驗統計分析[J].兵工學報, 2013, 34(12): 1603-1610.)

[4] Ismail A A. Inference for a step-stress partially accelerated life test model with an adaptive Type-II progressively hybrid censored data from Weibull distribution[J].JournalofComputationalandAppliedMathematics, 2014, 260(4): 533-542.

[5] Fard N, Li C H. Optimal simple step stress accelerated life test design for reliability prediction[J].JournalofStatisticalPlanningandInference, 2009, 139(1): 1799-1808.

[6] Meeker W Q, Escobar L A, Hong Y L. Using accelerated life tests results to predict product field reliability[J].Technometrics, 2009, 51(2): 146-161.

[7] Pan R. A Bayes approach to reliability prediction utilizing data from accelerated life tests and field failure observations[J].QualityandReliabilityEngineeringInternational, 2009, 25(2): 229-240.

[8] Wang Y S, Zhang C H, Chen X, et al. Statistical analysis of accelerated life testing for products with operational period[J].JournalofNationalUniversityofDefenseTechnology, 2008, 30(1): 94-98. (汪亞順,張春華,陳循,等.存在工作歷程產品的加速壽命試驗統計分析[J].國防科技大學學報,2008,30(1):94-98.)

[9] Tan Y Y, Zhang C H, Chen X, et al. Remaining life evaluation based on accelerated life testing[J].JournalofMechanicalEngineering, 2010, 46(2): 150-154. (譚源源, 張春華, 陳循, 等. 基于加速壽命試驗的剩余壽命評估方法[J].機械工程學報,2010,46(2):150-154.)

[10] Li L, Xu W. Reliability analysis for accelerated life test based on Weibull distribution[J].SystemsEngineeringandElectronics, 2010, 32(7): 1544-1548. (李凌, 徐偉. 威布爾產品加速壽命試驗的可靠性分析[J].系統工程與電子技術, 2010, 32(7): 1544-1548.)

[11] Anduin E T. Bayesian estimation of mixed Weibull distributions[J].ReliabilityEngineering&SystemSafety, 2009, 94(4): 463-473.

[12] Wang L Z, Jiang T M, Li X Y, et al. Lifetime evaluation method with integrated accelerated testing and field information[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013, 39(7): 947-951. (王立志, 姜同敏, 李曉陽, 等. 融合加速試驗及外場使用信息的壽命評估方法[J].北京航空航天大學學報, 2013, 39(7): 947-951.)

[13] Wang L Z, Pan R, Li X Y, et al. A Bayesian reliability evaluation method with integrated accelerated degradation testing and field information[J].ReliabilityEngineeringandSystemSafety, 2013, 112(4): 38-47.

[14] Jiang T M.Reliabilitytesttechnology[M]. Beijing: Beihang University Press, 2012: 194-205. (姜同敏. 可靠性試驗技術[M]. 北京: 北京航空航天大學出版社, 2012: 194-205.)

[15] Zhao Y.Dataanalysisofreliability[M]. Beijing: National Defense Industry Press, 2011: 103-106. (趙宇. 可靠性數據分析[M].北京: 國防工業出版社, 2011: 103-106.)

蔡忠義(1988-),男,博士研究生,主要研究方向為裝備可靠性與質量管理。

E-mail:afeuczy@163.com

陳云翔(1962-),男,教授,博士,主要研究方向為裝備發展論證、裝備RMS。

E-mail:cyx87793@163.com

王莉莉(1982-),女,講師,博士后,主要研究方向為裝備系統工程。

E-mail:bluechase@163.com

羅承昆(1991-),男,碩士研究生,主要研究方向為裝備管理與決策。

E-mail:afeulck@163.com

Method on reliability assessment with integrated field using and accelerated life data

CAI Zhong-yi, CHEN Yun-xiang, WANG Li-li, LUO Chen-kun

(EquipmentManagement&SafetyEngineeringCollege,AirForceEngineeringUniversity,Xi’an710051,China)

Abstract:Aiming at the mechanical & electrical product that its lifetime obeys to Weibull distribution and has used in field, a single-stress & time-switching step-stress accelerated life test is done to study the integrated assessment problem between field using data and accelerated life test (ALT) data. Considering the difference between field multi-stress environment and laboratory single-stress environment, a distribution parameter model with the correction factors is constructed. Statistical analysis for the integrated process of field using and the ALT is done. Its cumulative distribution function relationship under each stress is built. The maximum likelihood function of integrated filed using and ALT data is built. The data iteration method is used to determine the estimation value of unknown parameters. A certain mechanical & electrical product is used to design a simulation project. The sample data is obtained by Monte Carlo simulation. A contrastive analysis shows that the proposed model is more accurate.

Keywords:accelerated life test (ALT); reliability assessment; stress environment difference; correction factor; data integration

收稿日期：2015-04-14；修回日期：2015-09-05；網絡優先出版日期：2015-12-23。

基金項目：總裝“十二五”國防預先研究項目資助課題

中圖分類號：TB 114.3

文獻標志碼：A

DOI:10.3969/j.issn.1001-506X.2016.06.39

作者簡介：

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20151223.1116.032.html