Jacobi函數(shù)方程與Riemann ξ(s)函數(shù)零點

劉法勝

(山東科技大學(xué) 交通學(xué)院，山東 青島 266590)

Jacobi函數(shù)方程與Riemann ξ(s)函數(shù)零點

劉法勝

(山東科技大學(xué) 交通學(xué)院，山東 青島 266590)

摘要：利用Jacobi函數(shù)方程和Schwarz反射原理，給出Riemann zeta函數(shù)零點滿足的方程，進(jìn)而推得零點均落在實部為1/2的臨界線上。如此，所有與Riemann猜想等價的命題和以Riemann假設(shè)作為前提條件的結(jié)論都成立。

關(guān)鍵詞：黎曼猜想；Jacobi函數(shù)方程；反射原理

1研究背景

Riemann猜想(RH,Riemann hypothesis)源于Dirichlet級數(shù)函數(shù)：

(1.1)

其中：s=σ+it，Re(s)=σ>1。

文獻(xiàn)[1]和[2]列出了有關(guān)Riemann猜想的重大歷史事件。1737年，Euler給出了著名的乘積公式，即對所有大于1的實數(shù)s，有

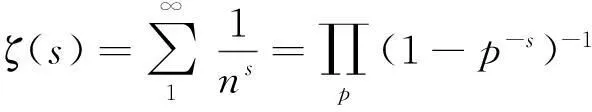
(1.2)

其中，N為自然數(shù)，p為素數(shù)。Euler乘法公式建立起了Dirichlet級數(shù)函數(shù)和素數(shù)分布的密切聯(lián)系，也可以說建立了自然數(shù)加法運算和素數(shù)乘積運算之間的一種聯(lián)系。

1792年，Guass提出后來被稱為素數(shù)定理的結(jié)論。1859年，Riemann在文獻(xiàn)[3]中，將(1.1)解析延拓到除s=1外的整個復(fù)平面上，并提出Riemann猜想：Riemann ζ函數(shù)的所有非平凡零點都在臨界線Re(s)=1/2上。

由Euler乘積公式(1.2)可以得到Riemann ζ函數(shù)在Re(s)>1的區(qū)域內(nèi)沒有零點。1896年，Hadamard和Poussion分別獨立證明了素數(shù)定理。素數(shù)定理等價于Riemann ζ函數(shù)在Re(s)=1上沒有零點。

1914年，丹麥數(shù)學(xué)家Bohr與德國數(shù)學(xué)家Landau證明了包含臨界線的無論多么窄的帶狀區(qū)域都包含了Riemann ζ函數(shù)的幾乎所有非平凡零點。同一年，英國數(shù)學(xué)家Hardy證明了Riemann ζ函數(shù)有無窮多個非平凡零點位于臨界線上。

1942年，挪威數(shù)學(xué)家Selberg證明了有正百分比的非平凡零點在臨界線上。Levinson在1974年證明了至少有34%的零點位于臨界線上。直到1989年，美國數(shù)學(xué)家Conrey證明了至少有40%的零點位于臨界線上。

RH之所以重要，其原因之一是RH有諸多重要等價命題和以其作為假設(shè)而成立的重要結(jié)論。文獻(xiàn)[2]中給出了32個重要等價命題；李修賢[4]在學(xué)位論文“Riemann猜想與素數(shù)分布”中專門羅列了34個與Riemann猜想等價結(jié)論。RH的各種等價結(jié)論和基于RH而成立的結(jié)論使人們有理由相信RH的正確性，因而，人們更愿意稱Riemann猜想為Riemann假設(shè)。

關(guān)于數(shù)值計算驗證或者說試圖舉出反例的工作，極大促進(jìn)了RH的相關(guān)研究。1932年，數(shù)學(xué)家Siegel從Riemann的手稿中獲得了重大發(fā)現(xiàn)——計算Riemann ζ函數(shù)非平凡零點的方法,稱為Riemann-Siegel公式。至1969年，350萬個零點得到驗證，全部位于臨界線上，這無疑大大增強了數(shù)學(xué)家們對RH的信心。到2004年，Gourdon用計算機驗證了Riemann ζ函數(shù)的前1013個零點都落在RH的臨界線上。

Riemann猜想的提出已經(jīng)過去近兩個世紀(jì)，而猜想是否成立，一直未得到肯定。RH被公認(rèn)為是“外行不懂，專家證明不了的世界難題”[2]。

Riemann的著名論文[3]“論小于給定數(shù)的素數(shù)分布”中已經(jīng)意識到猜想是成立的。令人惋惜的是，Riemann提出RH七年后就撒手人寰。考察提出RH的原始論文[3]發(fā)現(xiàn)，Riemann通過Jacobi函數(shù)方程，給出了Riemann ζ函數(shù)的解析延拓表達(dá)[5]21。Edwards[6],Karatsuba[7]都有用theta級數(shù)函數(shù)和Jacobi函數(shù)方程處理Riemann ζ函數(shù)解析延拓論述。Jacobi函數(shù)方程與Riemann ζ函數(shù)關(guān)系密切，前者自變量的倒數(shù)與后者變量的共軛變量對應(yīng)。Riemann原意就是要去證明RH，只是未能如愿，才以猜想的形式給出了著名的RH。倘若，Riemann當(dāng)時就沿著此路給出RH的證明，或者后來人及時補上其證明，或許RH不會如此出名。RH的諸多重要等價問題和基于RH的重要結(jié)果進(jìn)一步凸顯了RH的重要性，而等價問題的難以證明則說明，除了Riemann當(dāng)初猜想的基于Jacobi變換的思路外，恐怕還沒有發(fā)現(xiàn)更有效的思路。

現(xiàn)在可以說，RH的極限情形和具體零點計算，只是增大了RH成立的可能性，將Jacobi函數(shù)方程性質(zhì)和反射原理結(jié)合應(yīng)用是證明RH的有效方法。

2以Theta級數(shù)表達(dá)的Riemann ζ函數(shù)解析延拓顯表達(dá)

Dirichlet級數(shù)函數(shù)有多種解析延拓途徑，由于解析延拓的唯一性原理，各種延拓形式上不同，本質(zhì)上是等價的[5-7]。Riemann利用theta函數(shù)級數(shù)和Jacobi方程，將ζ函數(shù)解析延拓到除1之外的整個復(fù)數(shù)平面上[3，5]。

由于RH起源于Dirichlet級數(shù)函數(shù)的解析延拓，而基于theta級數(shù)表達(dá)的Riemann ζ函數(shù)解析延拓用到著名的Jacobi函數(shù)方程關(guān)系，為了本文的完整性和可讀性，此處以定理形式給出該既有結(jié)果[5]。

定理1[8]

(2.1)

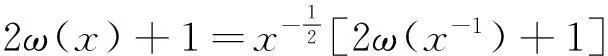
(2.2)

證明見文獻(xiàn)[8]188頁，也可參考文獻(xiàn)[5] 5～8頁給出的另一證明。

定理2[5]下述函數(shù)是Dirichlet級數(shù)函數(shù)在復(fù)平面上除s=1外的解析延拓:

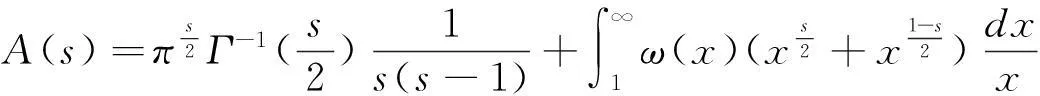
(2.3)

記A(s)=ζ(s),為Riemann ζ函數(shù)。鑒于該定理在RH中的重要性，此處給出其證明之一，詳細(xì)過程見文獻(xiàn)[5]11頁。

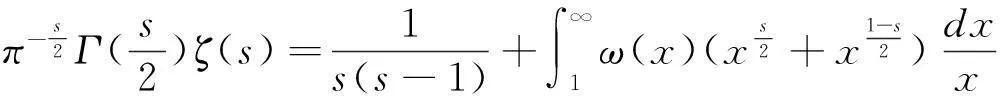
用積分公式表示Gamma函數(shù)，對于Re(s)>0和自然數(shù)N，有

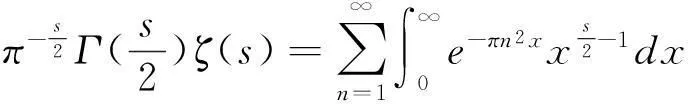
改變求和(∑)與積分(∫)的順序(絕對收斂可以改變順序)，則有

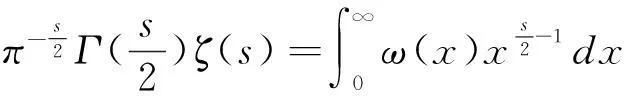
利用Jacobi方程(2.2)，并做積分變量x→x-1于下述第二個積分中，有

(2.4)

定理得證。

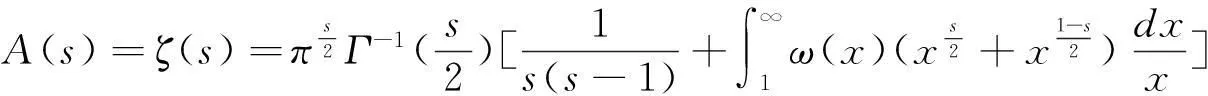
盡管對Dirichlet級數(shù)函數(shù)有多種解析延拓方法和形式，但由于解析延拓唯一性定理，它們本質(zhì)上是等價的。不同的解析延拓方式會有不同的方便之處，基于theta函數(shù)級數(shù)和Jacobi方程，將Dirichlet級數(shù)函數(shù)解析延拓為上述顯形式更方便。

至此，可以說，解析延拓后的Riemann ζ函數(shù)是整個復(fù)平面上除了簡單極點1(其留數(shù)為1)以外所有點上的解析函數(shù)。

現(xiàn)在，可以在復(fù)平面上考慮Riemann ζ函數(shù)的零點了。人們對其零點感興趣，是因為它們包含著素數(shù)的信息。然而，人們并非對Riemann ζ函數(shù)的所有零點都感興趣，所有實部在區(qū)間[0，1]外的平凡零點被列為RH陳述之外。

在討論其零點之前，先給出一個Riemann ζ函數(shù)的方程。注意到在A(s)中，把s與1-s作替換，等式成立。因此，有函數(shù)方程:

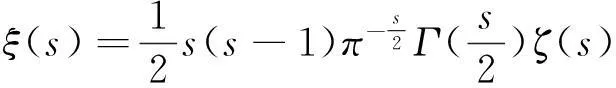
ξ(s)=ξ(1-s)。

(2.5)

記

(2.6)

3有關(guān)引理

為行文方便，給出以下引理[3，5]。

引理1設(shè)x是正實數(shù)，對多值對數(shù)函數(shù)只取其主枝，則

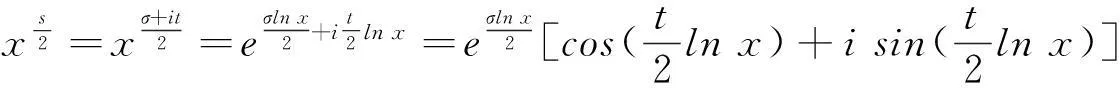
(3.1)

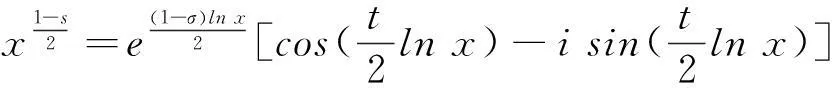
詳細(xì)的證明請參考文獻(xiàn)[5] 22頁定理1。前面的等價性證明可以由式(2.6)給出；后半部分的等價性由反射原理給出，因為這里在實數(shù)軸上函數(shù)取值為實數(shù)，故由Schwarz反射定理，得引理2。

引理3設(shè)t>0，則

(3.2)

證明：

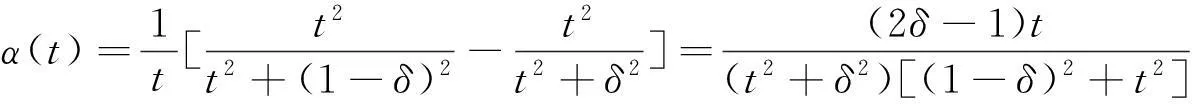
現(xiàn)在可以探討Riemann ξ(s)函數(shù)的零點了。

4Riemann ξ(s)函數(shù)的零點

由式(2.6)，設(shè)s=σ+it為Riemann ξ(s)的零點：

(4.1)

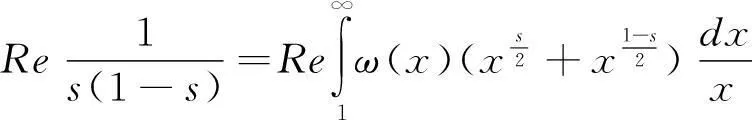
(4.2)

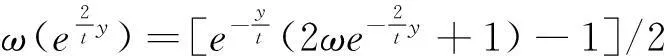
(4.3)

(4.4)

由式(4.3)可得

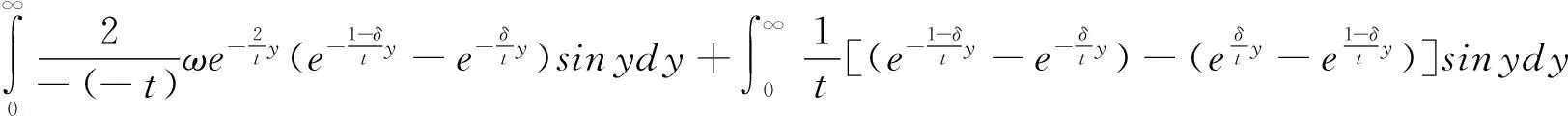
又由引理2，-t亦滿足式(4.4)

(4.5)

所以有

即

由引理3和引理4得

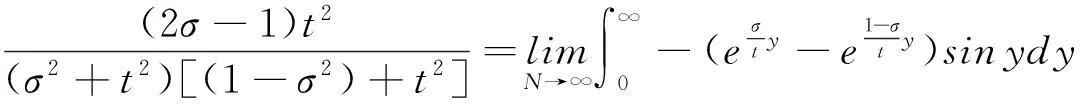
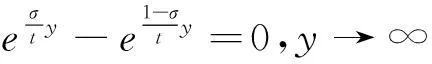
5Riemann ξ(s)函數(shù)零點計算

由式(4.2),下面函數(shù)的零點即為Riemann ξ(s)函數(shù)零點的虛部值：

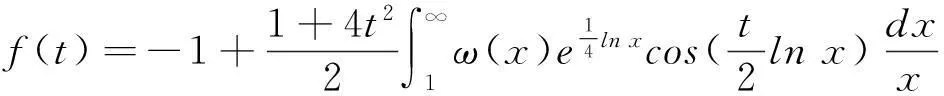
(5.1)

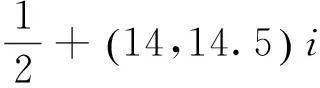
函數(shù)(5.1)包含了全部素數(shù)分布信息，素數(shù)分布性質(zhì)可以通過研究該函數(shù)的零點分布得到。

參考文獻(xiàn)：

[1]盧昌海.黎曼猜想漫談[M].北京:清華大學(xué)出版社,2012.

[2]BORWEIN P,CHOI S,ROONEY B.The Riemann hypothesis:A resource for the afficionado and virtuoso alike[M].New York:Springer,2008.

[3]RIEMANN B.über die Anzahl der Primzahlen unter einer gegebenen Gr?sse[M]//Gesammelte Mathematische Werke Und Wissenschaftlicher Nachlass.Berlin:Monats.Preuss,1859:671-680.

[4]李修賢.黎曼猜想與素數(shù)分布[D].濟南:山東大學(xué),2012.[5]KARATSUBA A A,VORONIN S M.The Riemann zeta-function[M].Translated by KOBLITZ N.Berlin:Walter de Gruyter,1992.

[6]EDWARDS H M.Riemann’s zeta function[M].New York:Dover Publications,Inc.,1974.

[7]TITCHMARSH E C.The theory of the Riemann zeta-function[M].Oxford:Clarendon Press,1951.

[8]EVEREST G,WARD T.An introduction to number theory[M].New York:Springer,2005.

(責(zé)任編輯：呂文紅)

Properties of Jacobi Functional Equation and Zeros of Riemann ξ(s)Function

LIU Fasheng

(College of Transportation,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)

Abstract:Using the properties of theta-series(Jacobi functional equation)and the Schwarz reflection principle,this paper presents an equation which meets the zeros of Riemann Zeta function and it is then deduced that all zeros are on the critical line where the real part is 1/2.Thus,all propositions equivalent to Riemann hypothesis and all conclusions with Riemann hypothesis as preconditions are true.

Key words:Riemann hypothesis(RH);Jacobi functional equation;reflection principle

收稿日期：2015-06-28

作者簡介：劉法勝(1957—)，男，山東臨朐人，教授，博士生導(dǎo)師，主要從事交通運輸規(guī)劃與管理方面的研究. E-mail：fashengliu@163.com

中圖分類號：O156.4

文獻(xiàn)標(biāo)志碼：A

文章編號：1672-3767(2016)01-0097-05