基于非均勻光滑有限元法的功能梯度壓電梁自由振動(dòng)分析

蔡斌，周立明(.吉林建筑大學(xué)　土木工程學(xué)院,吉林　長(zhǎng)春，308；.吉林大學(xué)　機(jī)械科學(xué)與工程學(xué)院,吉林　長(zhǎng)春，300)

?

基于非均勻光滑有限元法的功能梯度壓電梁自由振動(dòng)分析

蔡斌1，周立明2
(1.吉林建筑大學(xué)土木工程學(xué)院,吉林長(zhǎng)春，130118；2.吉林大學(xué)機(jī)械科學(xué)與工程學(xué)院,吉林長(zhǎng)春，130022)

摘要：為了提高求解功能梯度壓電材料動(dòng)響應(yīng)的精度，克服有限元系統(tǒng)剛度偏硬的缺點(diǎn)，提出非均勻Cell-based 光滑有限元法。基于單元的梯度光滑操作，考慮材料物性沿寬度方向呈梯度連續(xù)變化，推導(dǎo)非均勻Cell-based 光滑有限元法的基本公式，分析功能梯度壓電懸臂梁的材料物性參數(shù)遵循不同梯度分布規(guī)律時(shí)結(jié)構(gòu)自由振動(dòng)的固有頻率與振型，并與FEM求解結(jié)果進(jìn)行對(duì)比。研究結(jié)果表明：光滑梯度操作可降低有限元系統(tǒng)的剛度，非均勻Cell-based光滑有限元法的數(shù)值解更加接近真實(shí)解，從而可為功能梯度壓電材料的進(jìn)一步應(yīng)用提供參考。

關(guān)鍵詞：非均勻光滑有限元法；功能梯度壓電材料；自由振動(dòng)；梯度光滑技術(shù)

為了克服有限元系統(tǒng)剛度偏大的缺點(diǎn)，LIU等[1?2]提出了一些基于梯度光滑的有限元算法。NGUYENVAN等[3]將這種基于梯度光滑的有限元算法拓展到壓電領(lǐng)域，隨后，NGUYEN-XUAN[4]采用Edge-Based光滑有限元法對(duì)二維壓電結(jié)構(gòu)力學(xué)問題進(jìn)行了研究。通過數(shù)值分析，發(fā)現(xiàn)光滑有限元能夠提高求解精度，具有廣闊的應(yīng)用前景。工程中目前流行的壓電元件多為多層結(jié)構(gòu)，但元件中某些材料組分和物性的突然變化往往會(huì)導(dǎo)致器件在層間界面處存在明顯的局部應(yīng)力失配現(xiàn)象，導(dǎo)致黏結(jié)層在高溫易蠕變，在低溫易開裂，大大縮短了元件的壽命。為解決這類問題，ZHU等[5]將功能梯度的概念引入到壓電智能材料中，制備了功能梯度壓電材料，其兼具了壓電和梯度二者的優(yōu)點(diǎn)。此后，一些研究者[6?7]在功能梯度壓電材料這一領(lǐng)域開展研究。基于 Euler-Bernoulli 梁理論，F(xiàn)U[8]求解了功能梯度壓電梁熱?電屈曲的精確解；CHEN 等[9]基于Euler 梁理論，獲得了功能梯度壓電梁的自由振動(dòng)頻率；ZHAO等[10]采用無網(wǎng)格法求解了不同載荷作用下功梯度壓電板的靜態(tài)彎曲問題；KOMIJANI等[11]研究了功能梯度壓電材料執(zhí)行器非線性熱?機(jī)?電多場(chǎng)耦合響應(yīng)問題；DAI等[12]分析了功能梯度壓電材料的反平面裂紋問題；JODAEI 等[13]采用微分求積法求解了功梯度壓電板在不同邊界條件下靜態(tài)分析的三維彈性解。由于材料的非均勻性和多場(chǎng)耦合特性，使得求解功能梯度壓電元材料壓電方程[14?15]的難度大大增加，從而導(dǎo)致研究工作大多局限于靜力問題，對(duì)動(dòng)力學(xué)問題的研究仍然很少。本文作者針對(duì)功能梯度壓電懸臂梁，考慮材料特性沿寬度方向呈梯度連續(xù)變化，基于單元的梯度光滑操作，推導(dǎo)非均勻Cell-Based 光滑有限元(ICS-FEM)的基本公式，采用ICS-FEM分析功能梯度壓電懸臂梁自由振動(dòng)固有頻率與振型，并與FEM的計(jì)算結(jié)果進(jìn)行對(duì)比。

1　基本方程

功能梯度壓電材料問題的基本方程如下：

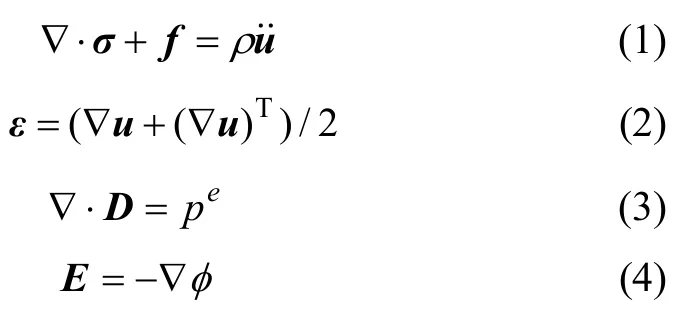
式中：CE為彈性模量張量；e 為壓電常數(shù)張量；g 為介電常數(shù)張量。對(duì) 于橫觀各向同性功能梯度壓電材料，x?z 平面為各向同性面，研究 x?z 平面內(nèi)力電耦合問題，滿足

則式(9)和式(10)的矩陣形式為

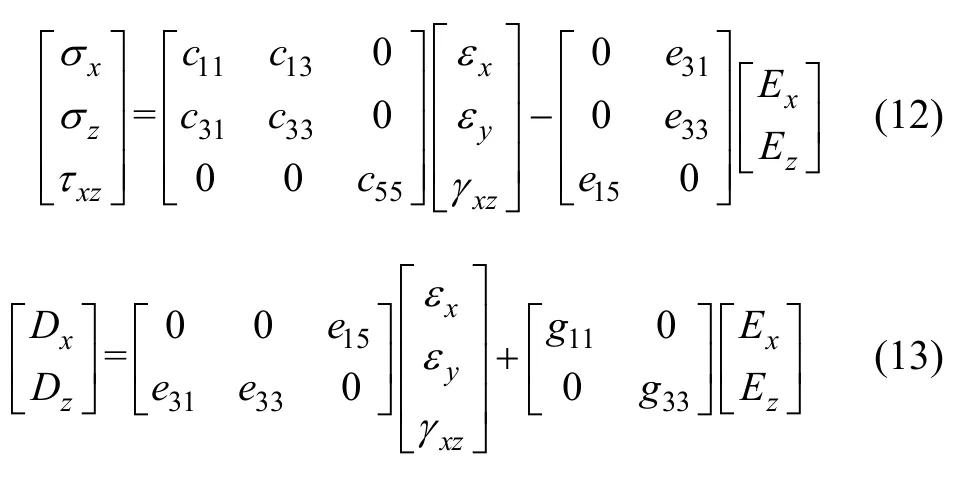
材料物性參數(shù)遵循如下梯度分布規(guī)律：

式中：M(z)為Cij，eij，gii和 ρ 等在結(jié)構(gòu)中的實(shí)際物理參數(shù)；Mb為功能梯度壓電材料結(jié)構(gòu)底部的物理參數(shù)；fb(z)為底部材料的體積分?jǐn)?shù)分布函數(shù)，見圖1。fb(z)一般有3種函數(shù)形式：

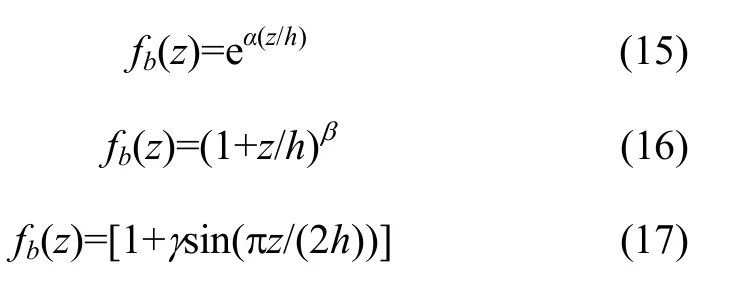
式中：α，β和γ分別為指數(shù)函數(shù)、冪函數(shù)和正弦函數(shù)分布規(guī)律的形狀因子；z為沿z軸坐標(biāo)；h為梁寬。

圖1　功能梯度壓電材料物參梯度分布圖Fig.1　Gradient distribution of functionally graded piezoelectric materials

2　非均勻Cell-based 光滑有限元法

將求解域離散成 np 個(gè)單元，包含 Nn個(gè)節(jié)點(diǎn)，每個(gè)單元內(nèi)的廣義位移u和廣義電勢(shì)φ 表示為

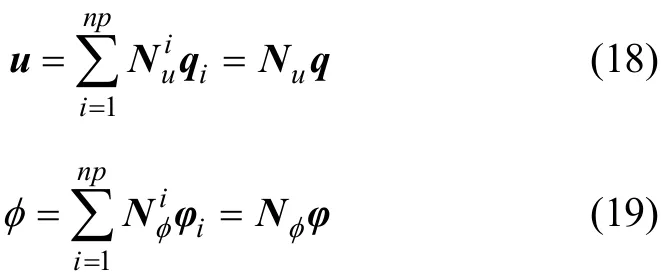
式中：Nu和 Nφ分別為 ICS-FEM 位移形函數(shù)和電勢(shì)形函數(shù)；q和?分別為節(jié)點(diǎn)位移向量和節(jié)點(diǎn)電勢(shì)向量。

圖2所示為四節(jié)點(diǎn)單元?jiǎng)澐譃?4個(gè)光滑子元的場(chǎng)節(jié)點(diǎn)、邊中間光滑節(jié)點(diǎn)、中心光滑節(jié)點(diǎn)、邊高斯點(diǎn)、外法向向量分布情況及形函數(shù)值。

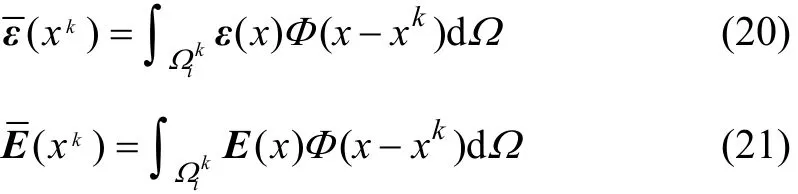
式中：ε(x)和 E(x)分別為FEM中的應(yīng)變和電場(chǎng)強(qiáng)度；Φ(x?xk)為光滑函數(shù)，

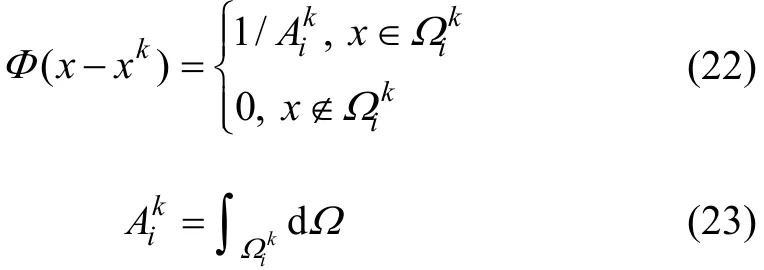
將式(22)代入式(20)和(21)，得

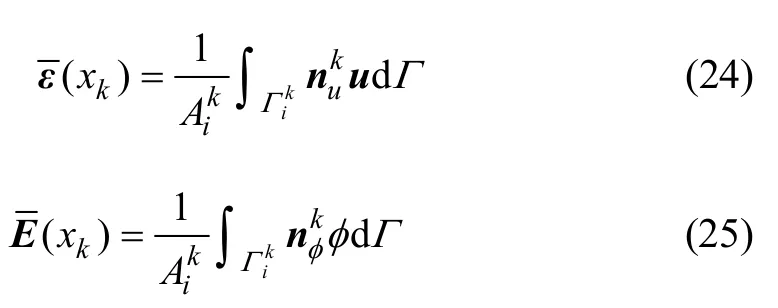
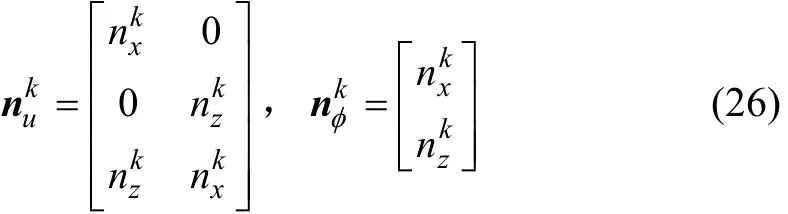
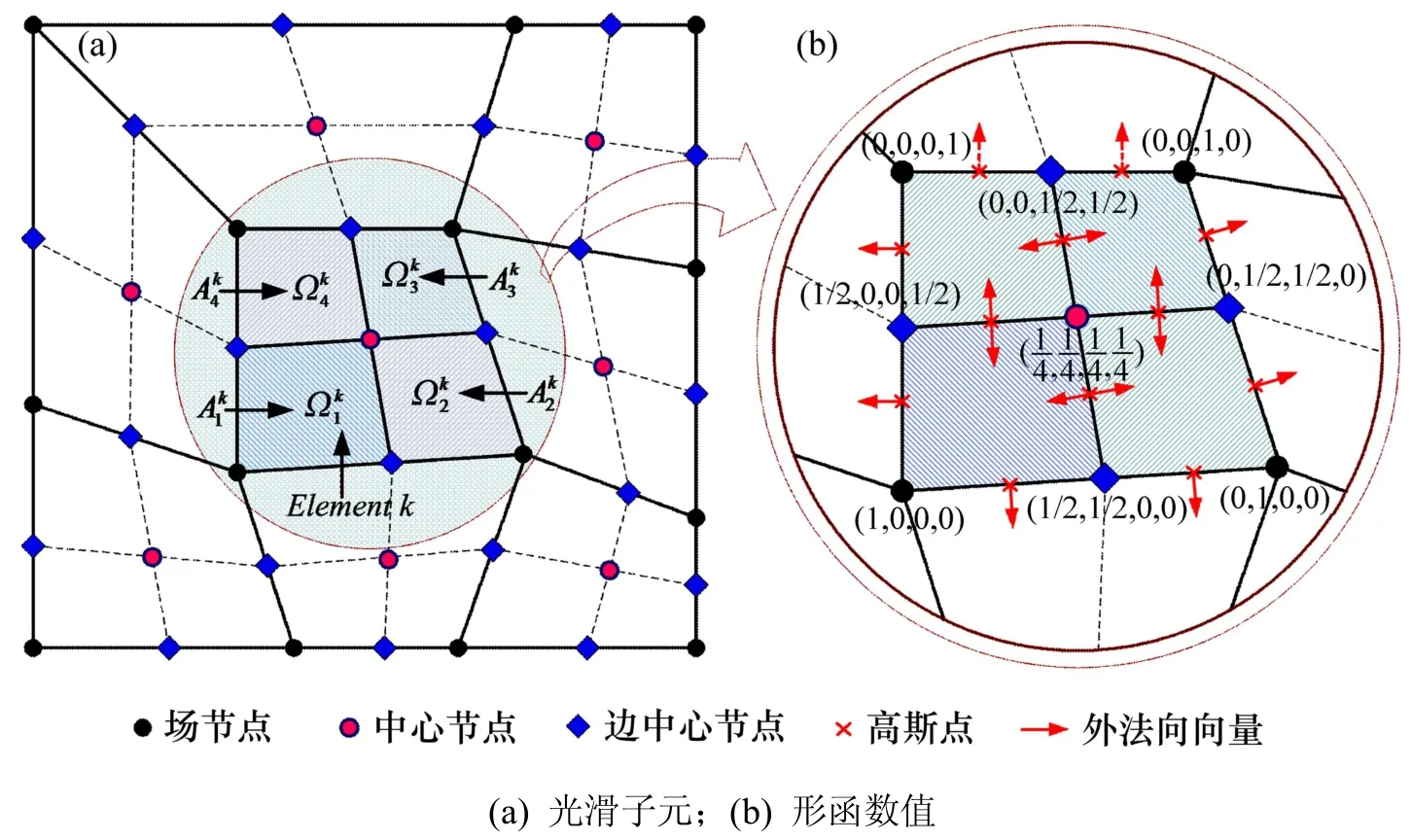
圖2光滑子元及形函數(shù)值Fig.2Smoothing subcells and values of shape functions

將式(24)和式(25)改寫為

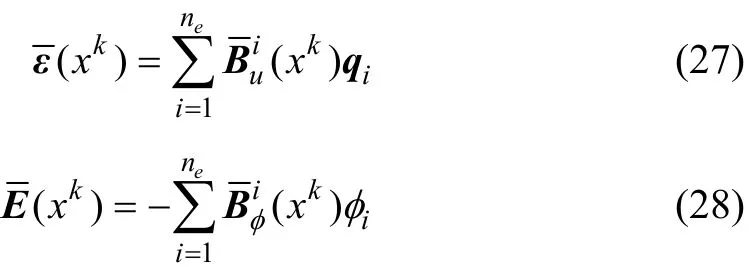
式中：ne為光滑子元個(gè)數(shù)；

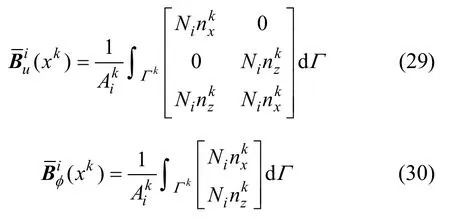
Ni為相關(guān)節(jié)點(diǎn)i的形函數(shù)。

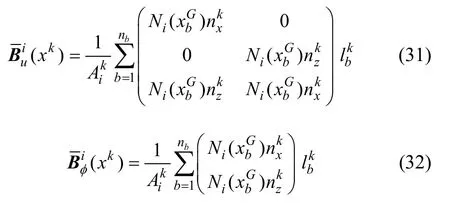
ICS-FEM與FEM的本質(zhì)差異為：FEM需要對(duì)單元形函數(shù)矩陣求導(dǎo)，則 ICS-FEM只需采用光滑元邊界高斯點(diǎn)處的形函數(shù)，不涉及形函數(shù)求導(dǎo)，降低了形函數(shù)的連續(xù)性要求，從而提高了計(jì)算方法的精度和收斂性。功梯度壓電耦合系統(tǒng)的動(dòng)力學(xué)模型可由 Hamilton原理導(dǎo)出，形式如下：

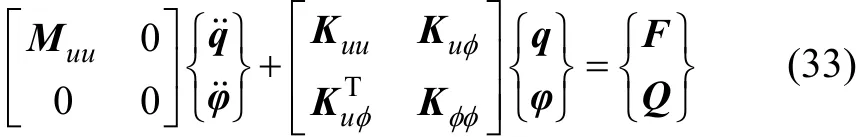
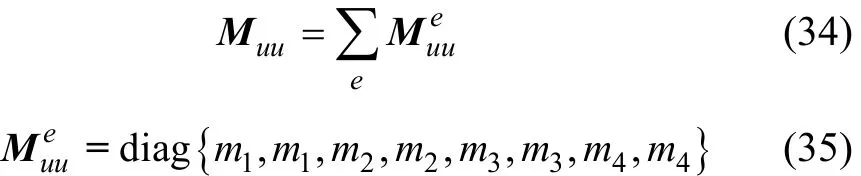
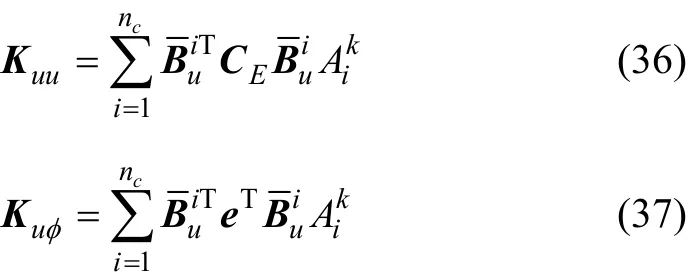
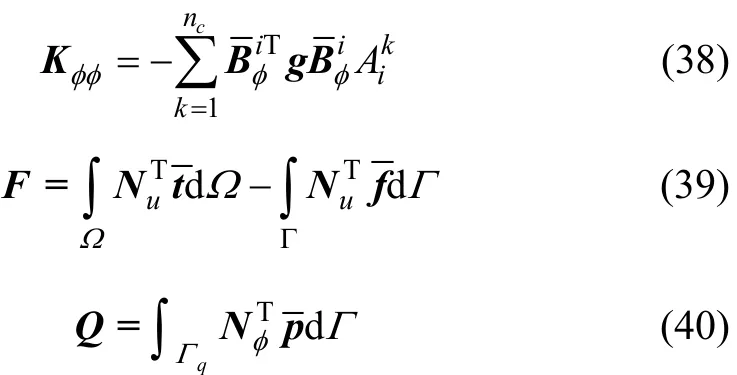
式中：nc=np×ne。采用非均勻光滑單元計(jì)算單元?jiǎng)偠染仃嚕?單元s中4個(gè)光滑子元(i=1,2,3,4)的物理參數(shù)不相同，直接取高斯積分點(diǎn)處的實(shí)際物理參數(shù)進(jìn)行計(jì)算，這樣可以使每個(gè)單元內(nèi)部也能夠體現(xiàn)材料屬性的變化。

由式(33)可知位移和電勢(shì)是耦合的。在分析特征值時(shí)，F(xiàn)=Q=0，先將和電勢(shì)相關(guān)的自由度進(jìn)行凝聚，

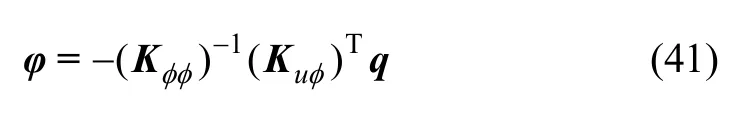
將式(41)代入式(33)，有

式中：

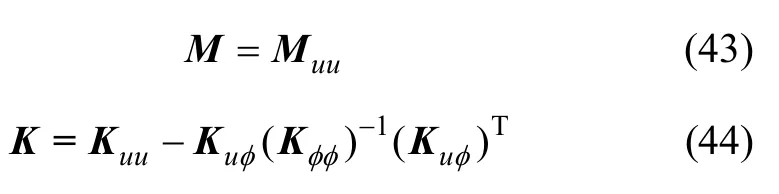
3　數(shù)值算例

3.1算例1

如圖3所示，一功能梯度壓電懸臂梁，長(zhǎng)度 L=20Cm，寬度 h=5Cm，厚度 b=1Cm。假設(shè)材料成分沿厚度方向呈梯度變化，考慮3種梯度分布形式：(Ⅰ)底部材料為 PZT-4，彈性系數(shù)、密度、壓電系數(shù)和介電系數(shù)均按指數(shù)函數(shù)變化，α=0.5；(Ⅱ)底部材料為 PZT-4，彈性系數(shù)、壓電系數(shù)和介電系數(shù)均按指數(shù)函數(shù)模式變化，α=0.5，密度按冪函數(shù)變化，β=0.5；(Ⅲ)底部材料為 PZT-4，彈性系數(shù)、壓電系數(shù)和介電系數(shù)均按指數(shù)函數(shù)變化，α=0.5，密度無變化。光滑子元個(gè)數(shù)取為 4，材料參數(shù)如表1所示，求解其固有頻率。

圖3　懸臂梁模型Fig.3　Geometry ofCantilever beam

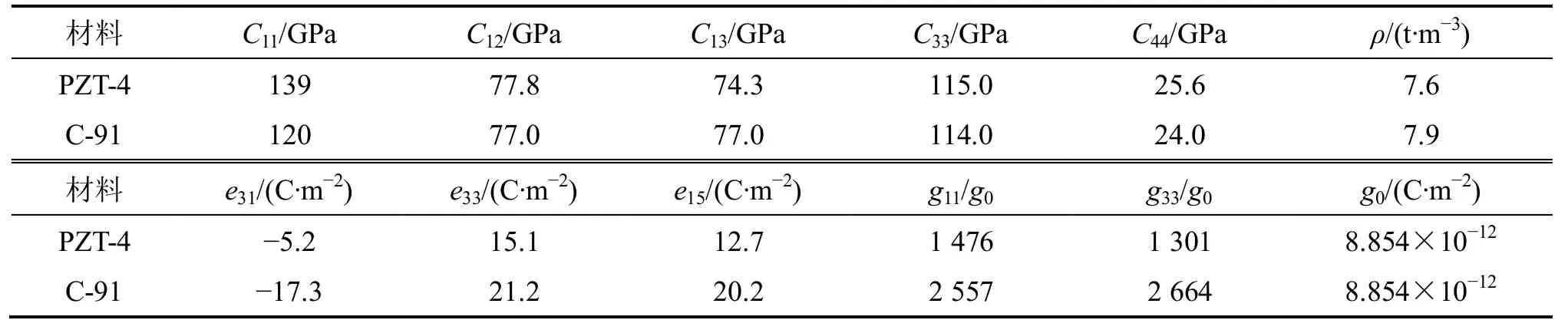
表1　材料常數(shù)Table1　MaterialConstants

表2所示為功能梯度壓電懸臂梁在 I，II和 III這3種材料梯度變化模式下，采用40×10均勻分布單元，由 ICS-FEM 和 FEM 求解得到的前5 階固有頻率。從表2可以看出：ICS-FEM計(jì)算得到的固有頻低于FEM求解的固有頻率，兩者的相對(duì)誤差最大為 2.85%，從而驗(yàn)證了ICS-FEM的正確性。CS-FEM不需對(duì)單元形函數(shù)矩陣求導(dǎo)，將求解域內(nèi)面積分改變?yōu)檫吔绶e分，形函數(shù)的連續(xù)性要求低。

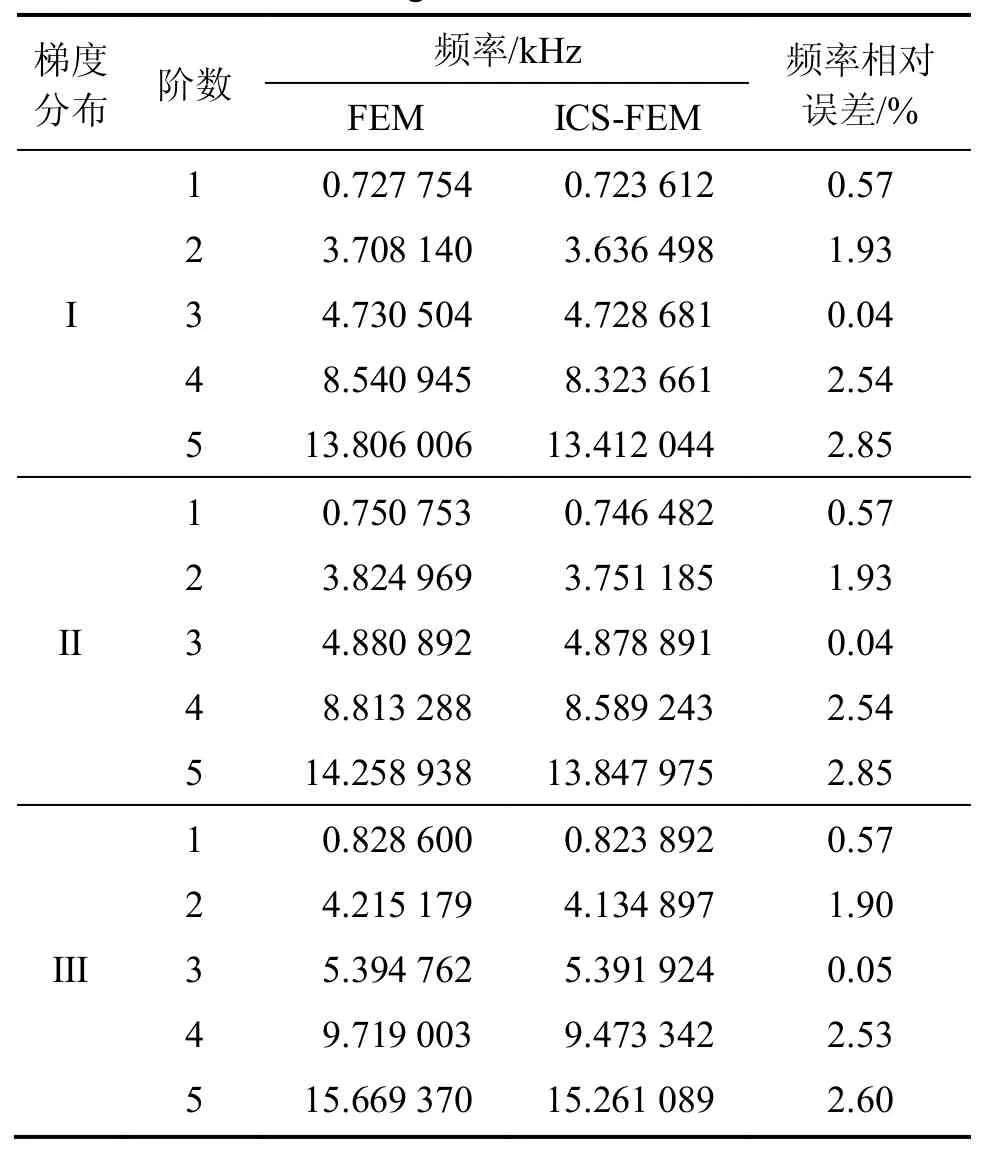
表2不同材料梯度分布形式下的前5階固有頻率Table1　First five natural frequency values of materials with different gradient distributions

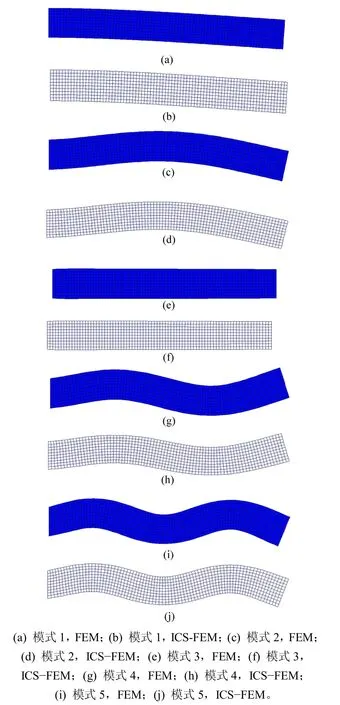
圖4功能梯度懸臂梁前5階振型Fig.4First five order modes of vibration of functionally gradient piezoelectricCantilevers

3.2算例2

功能梯度壓電懸臂梁，長(zhǎng)度L=40Cm，其他參數(shù)不變，底部材料為 PZT-4，頂部材料為C-91，彈性系數(shù)、密度、壓電系數(shù)和介電系數(shù)均按指數(shù)函數(shù)變化。材料參數(shù)如表1所示，求解其固有頻率和振型。

圖4所示為功能梯度壓電懸臂梁采用80×10均勻分布單元，由ICS-FEM和 FEM 求解得到的前5 階固有振型。從圖4可看出：兩者振型相吻合。這進(jìn)一步驗(yàn)證了ICS-FEM的正確性和有效性。

表3所示為功能梯度壓電懸臂梁采用80×10均勻分布單元，由ICS-FEM和 FEM 求解得到的前5 階固有頻率，以 Ansys 采用 320×40單元所得結(jié)果作為參考解。從表3可以看出：在同樣單元條件下，ICS-FEM計(jì)算得到的固有頻率低于 FEM 求解的固有頻率，其數(shù)值解更加接近真實(shí)解，從而驗(yàn)證了ICS-FEM可降低有限元系統(tǒng)剛度，提高求解精度，有效地求解功能梯度壓電結(jié)構(gòu)的動(dòng)響應(yīng)問題。

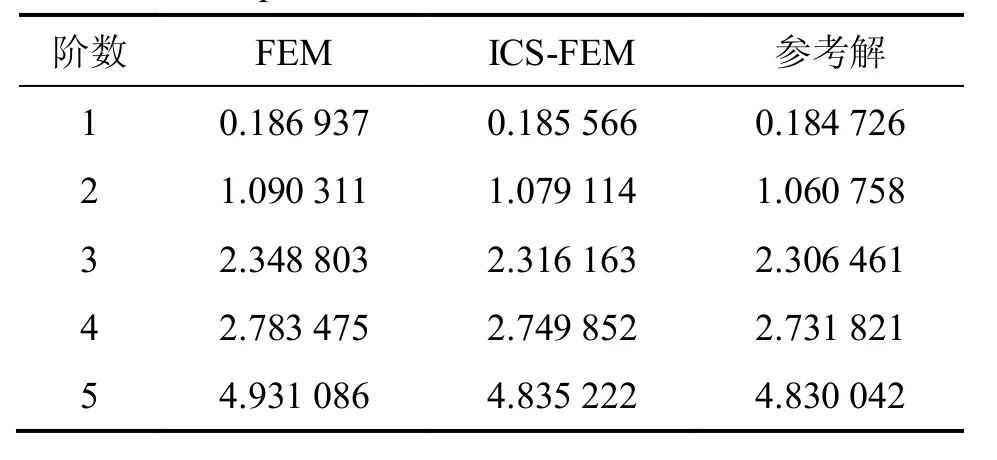
表3　功能梯度壓電懸臂梁的前5階固有頻率Table1　First five natural frequency of functionally gradient piezoelectricCantilevers　kHz

4　結(jié)論

1)ICS-FEM 求解功能梯度壓電結(jié)構(gòu)的動(dòng)響應(yīng)問題是正確的、有效的。

2)ICS-FEM可降低有限元系統(tǒng)剛度，在相同單元條件下，其計(jì)算精度高于 FEM 模擬結(jié)果的精度，更接近真實(shí)值。

參考文獻(xiàn)：

[1]LIU G R,DAI K Y,NGUYEN T T.A smoothed finite element method for mechanics problems[J].Comput Mech,2007,39(6): 859?877.

[2]LI ERIC,HE ZC,CHEN L,et al.An ultra-accurate hybrid smoothed finite element method for piezoelectric problem[J].Engineering Analysis with Boundary Elements,2015,50:188?197.

[3]NGUYEN-VAN H,MAI-DUY N,TRAN-CONG T.A nodebased element for analysis of planar piezoelectric structures[J].CMES:Computer Modeling in Engineering and Sciences,2008,36(1): 65?95.

[4]NGUYEN-XUAN H,LIU G R,NGUYEN-THOI T,et al.An edge-based smoothed finite element method for analysis of two-dimensional piezoelectric structures[J].Smart Materials and Structures,2009,18(6): 065015.

[5]ZHU Xinhua,MENG Zhongyan.Operational principle,fabrication and displacementCharacteristics of a functionally gradient piezoelectricCeramic actuator[J].Sensors and Actuators A: Physical,1995,48(3):169?176.

[6]KOMIJANI M,REDDY J N,ESLAMI M R.Nonlinear analysis of microstructure-dependent functionally graded piezoelectric material actuators[J].Journal of the Mechanics and Physics of Solids,2014,63: 214?227.

[7]ZHOU Liming,MENG Guangwei,LI Feng,et al.Cell-based smoothed finite element method-virtualCrackClosure technique for a piezoelectric material ofCrack[J].Mathematical Problems in Engineering,2015: 371083.

[8]FU Yiming,WANG Jianzhe,MAO Yiqi.Nonlinear analysis of buckling,free vibration and dynamic stability for the piezoelectric functionally graded beams in thermal environment[J].Applied Mathematical Modelling,2012,36(9): 4324?4340.

[9]CHEN Haiyan,JIN Dengren,MENG Zhongyan.DynamicCharacteristics of functionally gradient piezoelectric actuators [C]//Properties and Applications of Dielectric Materials.Xi’an,China: IEEE,2000: 983?987.

[10]ZHAO X,LEE Y Y,LIEW K M.Free vibration analysis of functionally graded plates using the element-free method[J].Journal of Sound and Vibration,2009,319(3): 918?939.

[11]KOMIJANI M,REDDY J N,ESLAMI M R.Nonlinear analysis of microstructure-dependent functionally graded piezoelectric material actuators[J].Journal of the Mechanics and Physics of Solids,2014,63(1): 214?227.

[12]DAI Yao,CHONG Xiao,LI Shimin.The higher orderCrack tip fields for anti-planeCrack in functionally graded piezoelectric materials[J].Applied Mechanics and Materials,2014,472: 617?620.

[13]JODAEI A.3D elasticity solution for static analysis of functionally graded piezoelectric annular plates on elastic foundations using SSDQM[J].Mechanica,2014,49(1): 215?237.

[14]LEZGY-NAZARGAH M,VIDAL P,POLIT O.An efficient finite element model for static and dynamic analyses of functionally graded piezoelectric beams[J].Composite Structures,2013,104: 71?84.

[15]LI Y S,FENG W J,CAI Z Y.Bending and free vibration of functionally graded piezoelectric beam based on modified strain gradient theory[J].Composite Structures,2014,115(1): 41?50.

(編輯 陳燦華)

Inhomogeneous smoothed finite element method for free vibration analysis of functionally gradient piezoelectricCantilevers

CAI Bin1, ZHOU Liming2
(1.School ofCivil Engineering,Jilin Jianzhu University,Changchun130118,China? 2.School of Mechanical Science and Engineering,Jilin University,Changchun130022,China)

Abstract:In order to improve the solving precision of dynamic response problems of functionally gradient piezoelectric materials and soften the “over-stiffness”,an inhomogeneousCell-based smoothed finite element method was presented.Based on gradient smoothing technique of elements andConsidering theChange of gradient of material properties only in the breadth direction,the basic formula of inhomogeneousCell-based smoothed finite element(ICS-FEM)was derived.Using this proposed method,free vibrationCharacteristics of the functionally graded piezoelectricCantilever were analyzed when the material parameters followed different gradient distributions.The accuracy of the proposed method wasConfirmed byComparing the FEM results.The results show that the gradient smoothing techniqueCan reduce the stiffness of the finite element system and improve the accuracy of the solution for electromechanicalCoupling systems by using ICS-FEM,which provides reference for further application ofCell-based smoothed finite element method.

Key words:inhomogeneous smoothed finite element method? functionally graded piezoelectric materials? free vibration? gradient smoothing technique

中圖分類號(hào)：TB115

文獻(xiàn)標(biāo)志碼：A

文章編號(hào)：1672?7207(2016)01?0048?06

DOI:10.11817/j.issn.1672-7207.2016.01.008

收稿日期：2015?03?10；修回日期：2015?05?08

基金項(xiàng)目(Foundation item)：國(guó)家自然科學(xué)基金資助項(xiàng)目(51305157)；吉林省科技廳基金資助項(xiàng)目(20130305006GX)(Project(51305157)supported by the National Natural Science Foundation ofChina? Project(20130305006GX)supported by Department of Science and Technology Fund of Jilin Province)

通信作者：周立明，博士，講師，從事計(jì)算固體力學(xué)研究；E-mail: lmzhou@jlu.edu.cn