鋼筋混凝土梁疲勞累積損傷過程的等效靜力分析方法

王青，衛軍，劉曉春，徐港(1.中南大學 土木工程學院，湖南 長沙，410075；.三峽地區地質災害與生態環境湖北省協同創新中心，湖北 宜昌，44300；3.高速鐵路建造技術國家工程實驗室，湖南 長沙，410075)

?

鋼筋混凝土梁疲勞累積損傷過程的等效靜力分析方法

王青1,2,3，衛軍1,3，劉曉春1,3，徐港2
(1.中南大學 土木工程學院，湖南 長沙，410075；2.三峽地區地質災害與生態環境湖北省協同創新中心，湖北 宜昌，443002；3.高速鐵路建造技術國家工程實驗室，湖南 長沙，410075)

摘要：為了實現對鋼筋混凝土梁疲勞性能的全過程分析和剩余承載力評估，提出一種混凝土構件疲勞累積損傷過程的等效靜力分析方法。通過對材料疲勞剛度、強度退化和疲勞殘余變形累積發展規律進行分析研究，建立混凝土和鋼筋任意加載次數后的疲勞本構模型；基于混凝土材料在靜態荷載與疲勞荷載作用下破壞的相似性，構建疲勞荷載與靜載作用的等效關系，提出鋼筋混凝土構件疲勞性能的等效靜力分析方法。采用該方法對某混凝土試驗梁進行疲勞性能分析。研究結果表明：所獲得的數值模擬結果與實驗值變化規律一致，吻合程度良好，驗證了該方法的有效性和實用性。

關鍵詞：鋼筋混凝土；疲勞本構模型；等效靜力分析；數值模擬

混凝土梁承受重復荷載作用將引起疲勞損傷，對其使用壽命和安全性都會產生嚴重影響。長期以來，人們主要通過室內疲勞試驗，對混凝土梁的疲勞性能進行研究，但疲勞試驗非常耗資費時，且不易進行足尺構件試驗，尺寸效應難以克服，同時也難以模擬結構實際所經歷的疲勞作用。近年來，隨著數值仿真技術的發展，結構疲勞數值模擬的方法逐漸為研究者所采用。利用現有的疲勞分析軟件雖然可以較好地預測結構的疲勞壽命，但仍無法對結構疲勞一定次數后的力學性能作出評判，更無法進行疲勞全過程分析。一些學者采用有限單元法(或條帶法)對混凝土構件的疲勞損傷過程進行了仿真分析[1?3]，有些還對高周疲勞工況下的加載次數按照一定原則進行了簡化，大大降低了計算工作量，但通常疲勞殘余應變的累積、疊加和平衡迭代需通過編寫專用程序或軟件二次開發實現，通用性不強。為此，本文作者在對材料疲勞剛度、強度退化和疲勞殘余變形累積發展規律進行分析總結的基礎上，基于“變形唯一性”假定和混凝土材料在靜態荷載與疲勞荷載作用下破壞的相似性，以殘余應變作為等效參量，建立疲勞荷載與靜載分析的等效關系，由1次靜力加卸載構造出與疲勞N次損傷等效的狀態梁，進而引入材料的疲勞損傷本構模型，建立構件受疲勞荷載作用的等效靜力分析方法，基于ABAQUS有限元軟件平臺高效地實現高周疲勞荷載作用下鋼筋混凝土梁的疲勞累計損傷過程分析和剩余承載力預測。

1　疲勞本構模型

1.1混凝土疲勞本構模型

1.1.1疲勞損傷后的應力?應變關系

混凝土在重復加卸荷作用下，疲勞損傷引起混凝土材性的退化主要表現為混凝土殘余靜強度和峰值應變降低、混凝土剛度衰減和殘余變形增加[4]。以混凝土靜力條件下的單軸受壓本構模型[5]為基礎，綜合考慮混凝土疲勞剛度退化、疲勞強度退化和疲勞殘余應變的演化規律，并忽略疲勞加載過程中卸載與再加載曲線之間可能存在的滯回現象，可通過試驗回歸法構建混凝土任意疲勞加載次數后的受壓本構模型：

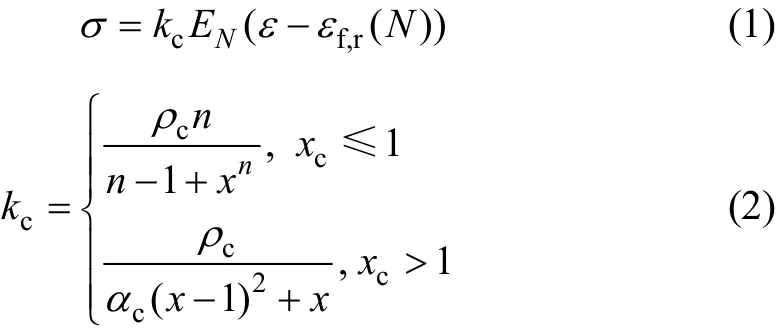
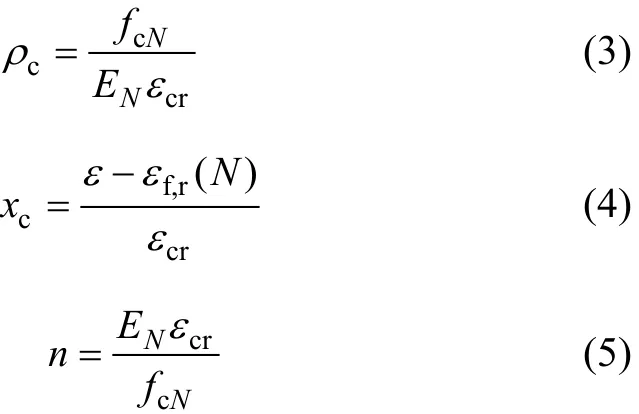
同理，可基于規范中單軸受拉的應力應變關系構建出N次疲勞后混凝土受拉本構模型：

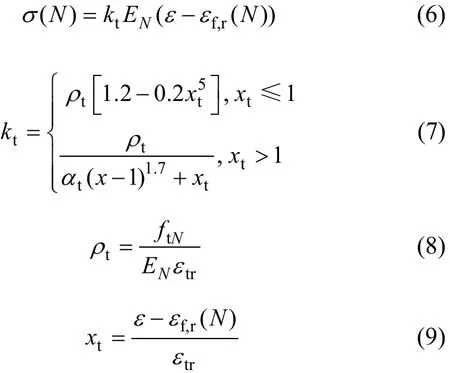
式中：σ 和ε 分別為受壓(拉)混凝土應力和應變；kc和kt分別為受壓和受拉疲勞損傷演化的參數；αc和 αt為疲勞后應力應變曲線中下降段的形狀參數，假定下降段曲線與靜載應力應變曲線的下降段有相同的形狀參數[5]，可參考文獻[6]中表C.2.4 取值；εf,r(N)為第 N次加卸載后的殘余應變；EN為疲勞N次后退化了的混凝土彈性模量；fcN，ftN，εcr和 εtr分別為疲勞 N 次后混凝土的剩余抗壓、抗拉疲勞強度和第N次加載的峰值壓應變、峰值拉應變，這些參數的確定是進行疲勞分析的關鍵，具體確定方法如下。

1.1.2疲勞殘余應變

隨著疲勞荷載次數增加，混凝土殘余應變不斷增加，且其值與疲勞荷載次數、應力水平等有關。現有的疲勞殘余變形模型較多,主要可以分為：考慮應力比的疲勞殘余變形模型和不考慮應力比的疲勞殘余變形模型，相關參數可由試驗回歸分析得到。在沒有更多試驗數據供分析的情況下，采用下列不考慮應力比的公式計算疲勞加卸載N次后混凝土受壓的縱向殘余變形εf,r(N)[3]：

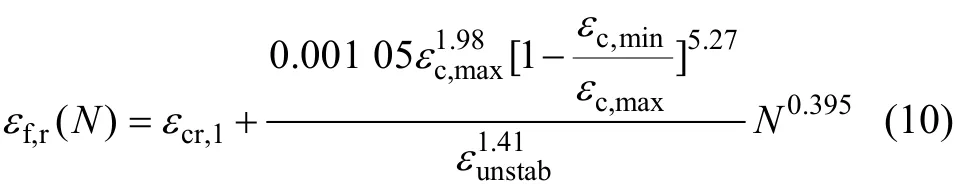
式中：εcr,1為第1次應力循環所引起的殘余變形；εc,min和εc,max分別為荷載下限、 荷載上限作用下的初始瞬時應變；εunstab為疲勞變形第3階段開始時混凝土的縱向總變形，取決于混凝土本身材料的性質，常取為1次加載破壞時的峰值應力所對應的應變ε0。

1.1.3剛度退化

混凝土彈性模量的退化是衡量構件剛度退化的重要指標。試驗研究發現，混凝土疲勞彈性模量的變化隨加載次數增加呈 3個階段：第1階段，彈性模量衰減較快；第2階段，彈性模量呈穩定線性退化，該階段疲勞應力占總疲勞壽命的75%～80%；第3階段，彈性模量急劇不穩定衰減，直至疲勞破壞[7]。文獻[8]通過大量的試驗研究，得到第2階段混凝土彈性模量與疲勞次數間滿足如下關系：

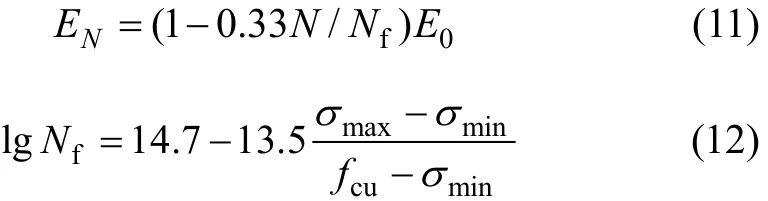
其中：E0為混凝土初始彈性模量；EN為疲勞N次后的混凝土彈性模量；Nf為疲勞壽命[9],按照文獻[11]取值；σmin和 σmax分別為荷載下限、荷載上限作用下的初始瞬時應力；fcu為混凝土的立方體抗壓強度。

1.1.4強度退化

通過試驗研究發現：對于某一給定的循環次數，疲勞強度不僅取決于循環中的最大應力，而且取決于最小應力。根據文獻[10]的研究結果，混凝土受壓疲勞次數 N 與壓應力上限 σc,max(即剩余疲勞抗壓強度fcN)以及壓應力下限 σc,min的關系可表述成如下形式：

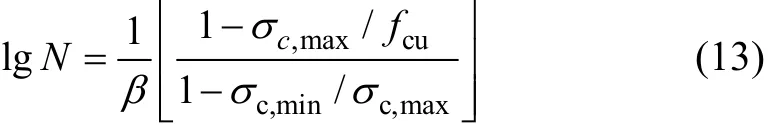
式中：β 為混凝土的材料常數，取值范圍為 0.064～ 0.080，一般通過試驗回歸分析得到，在沒有充足實驗數據的情況下，可取為平均值0.072。混凝土受拉疲勞次數N與拉應力上限σt,max(即剩余疲勞抗拉強度ftN)以及拉應力下限σt，mi n的關系可表述成如下形式[10]：

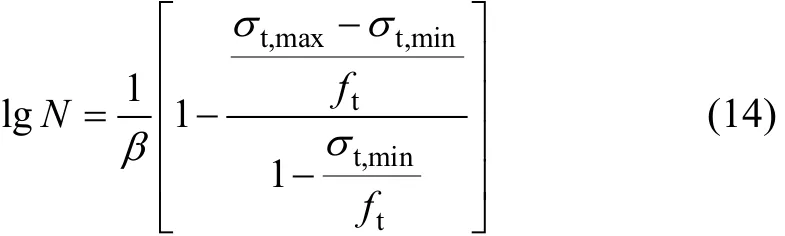
式中：ft為混凝土的靜態抗拉強度。確定fcN和ftN后，據規范表C.2.4[5]即可求得相應疲勞次數作用后的混凝土峰值壓應變εcr和峰值拉應變εtr。

1.2鋼筋的疲勞本構模型

鋼筋高周疲勞的應力水平通常較低，未達到屈服強度，受力和變形基本處于彈性階段，因此，一般認為鋼筋彈性模量在整個疲勞加載過程中不發生退化，殘余應變可以忽略。考慮到鋼筋疲勞破壞是由于剩余有效承載面積不能承擔拉伸荷載而產生的瞬態斷裂，因此，常通過減小橫截面積研究鋼筋抗力性能隨疲勞次數的降低規律。文獻[11]根據 Miner 線性累積損傷準則，得到疲勞 N 次后鋼筋的有效截面積可由下式計算：

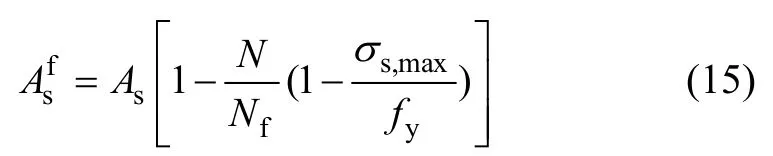
式中：As為鋼筋的初始橫截面積；fy為普通鋼筋的屈服強度(或預應力鋼筋的極限抗拉強度)；σs,max為疲勞加載過程中鋼筋的應力最大值。

假定鋼筋在 N 次重復應力作用后發生了疲勞破壞，則鋼筋在疲勞破壞時應滿足下式：

將式(15)代入式(16)，可將有效面積換算為鋼筋的等效剩余疲勞強度fs,N。基于鋼筋的理想彈塑性模型，認為等效剩余屈服強度 fy,N與等效剩余疲勞強度 fs,max相等，即

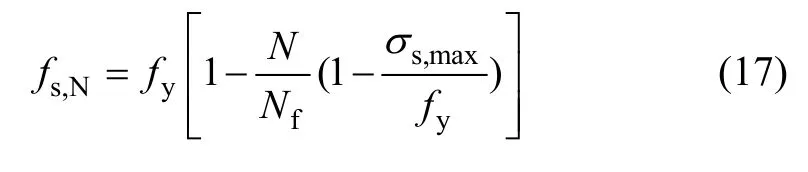
2　混凝土結構疲勞加載與靜載的等效損傷狀態

疲勞加載次數通常是上百萬次，若逐步計算則工作量巨大。眾多研究成果表明：混凝土材料無論在靜態荷載還是疲勞荷載作用下，其破壞過程均是裂縫在界面過渡區和基體中演化、發展的過程[12]。若能利用混凝土材料在靜載與疲勞荷載作用下破壞的相似性，依據某等效參量建立疲勞荷載與靜載分析的等效關系，則可由1次靜力加卸載構造出與疲勞N次損傷等效的狀態梁，進而引入材料的疲勞本構模型，實現對疲勞N次后結構受力性能的數值分析。若取不同的疲勞次數Ni進行等效靜力分析，則可以得到任意疲勞次數后混凝土結構的裂縫、損傷、變形、應變、應力等的發展情況，由此實現高周疲勞荷載作用下鋼筋混凝土梁的全過程分析。

2.1等效參量的選擇

混凝土變形唯一性假設是 SINHA 等[13]提出的。該假設認為不管以前承受的重復荷載歷程如何，只要殘余變形相同，則在此基礎上施加相同的重復荷載，其荷載與變形的關系將保持不變，而與以前的荷載變形歷程無關。這一假設目前已被許多試驗所證實。文獻[6,14]的研究也認為，殘余應變反映了混凝土的微塑性變形和微裂紋不可恢復程度，所以，比其他參數更能反映材料本身的損傷特性。為此，本文進行如下假定：設經過1次靜力加載P1(P1＞Pmax)并卸載后的混凝土梁為狀態1，受壓邊緣混凝土殘余壓應變為 εr；經歷N次Pmin～Pmax疲勞荷載作用并卸載后的同一混凝土梁為狀態2，受壓邊緣混凝土殘余壓應變為εf,r(見圖1)；若二者的殘余應變相等即 εr＝εf,r，則可認為經歷了1次靜力加卸載路徑A的狀態1混凝土和經歷了疲勞加卸載路徑B的狀態2混凝土的能量耗散相同，損傷等效。

圖1　等效狀態示意圖Fig.1　Diagram of equivalent state

若不考慮鋼筋、混凝土之間的黏結性能退化及其相對滑移，則鋼筋應變與該位置的混凝土應變相等，狀態1與狀態2的鋼筋應變相等，應力相同，受力狀態等效。為此，以混凝土受壓區殘余應變作為等效參量建立疲勞加載與靜力加載的等效損傷狀態，將經歷了N次Pmin～Pmax疲勞加卸載的狀態1梁等效為1次性靜力加載至P1后卸載的狀態2梁，并在此基礎上進行鋼筋混凝土梁疲勞加載后的受力分析。若根據各階段特點取不同的疲勞次數Ni進行等效靜力分析，則可以得到任意疲勞次數后混凝土結構的裂縫、損傷、變形、應變、應力等的發展情況，由此實現高周疲勞荷載作用下鋼筋混凝土梁的全過程分析。

2.2靜力加載中殘余應變的計算模型及其等效狀態的構建

由圖1可知，靜力加載中混凝土殘余應變 εr可由下式求得：

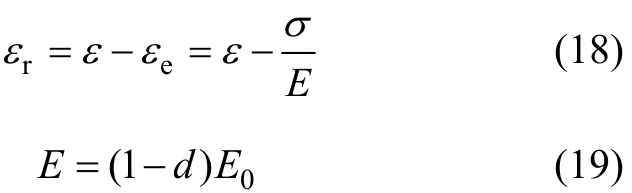
式中：ε，εe和εr分別為加載至任意一點的混凝土總應變、彈性應變和殘余塑形應變；E為加載至任一點的混凝土卸載彈性模量(如圖1所示)；E0為初始彈性模量；d 為損傷因子，由加卸載試驗確定，如缺少試驗數據，也可應用能量等效原理，由

計算[15]。綜上可知：基于前述疲勞損傷后的混凝土應力?應變關系，由式(18)～(20)可求得靜力加載至任意一點的混凝土殘余塑性變形 εr，再結合式(10)，令εf,r(N)=εr，即可由殘余應變建立與疲勞加載路徑 B 等效的1次靜力加卸載路徑A。

3　材料的疲勞失效準則

3.1混凝土的疲勞失效準則

在疲勞荷載作用下，混凝土內部的原始缺陷不斷擴展。相關研究[14]表明：當疲勞后殘余應變 εf,r達到0.4 倍的靜載極限壓應變 ε0(ε0為混凝土靜載極限強度fc對應的應變)時，混凝土已經有很嚴重的損傷，不能再繼續工作，就認為混凝土發生疲勞破壞，即混凝土在疲勞荷載作用下的疲勞失效準則為

令 εf,r(N)=εr，則可得到等效至靜力加載中的混凝土疲勞失效準則：

3.2鋼筋的疲勞失效準則

鋼筋是以脆性斷裂為疲勞破壞的標志，一般是以鋼筋應力幅值是否超過疲勞破壞的允許應力幅值作為鋼筋疲勞破壞依據。如對于HRB400鋼筋，可參考文獻[11]中的S?N方程確定。

4 疲勞荷載作用下的結構分析過程

基于前述計算模型和有限元分析方法，N 次疲勞后的結構受力性能分析流程如圖2所示。若需要對疲勞過程中結構的各部分應力、應變、變形等進行全過程跟蹤分析，則可根據各階段特點取不同的疲勞次數Ni按照上述流程進行數值模擬計算，以得到任意疲勞次數后混凝土結構的應變、應力、變形情況，也可根據ABAQUS軟件處理的損傷場(即損傷因子)分布推得結構中的裂縫發展趨勢。

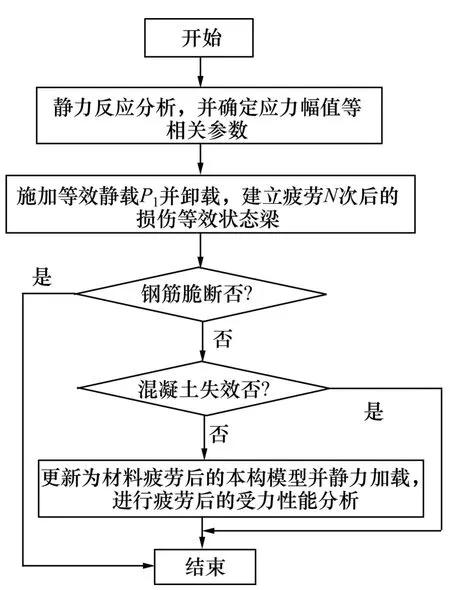
圖2疲勞后力學性能的等效靜力分析方法流程圖Fig.2Flow-process diagram of equivalent static analysis method on fatigue behavior

5 算例驗證

文獻[16]進行了鋼筋混凝土簡支梁疲勞性能試驗研究。以其中B40系列試驗梁為例，該梁混凝土強度等級為C40，彈性模量為3.82×104MPa，幾何尺寸及配筋如圖3所示。

基于前述分析步驟采用 ABAQUS 軟件進行數值分析。仿真模型中混凝土與鋼筋分別選用C3D8R 和T3D2 單元模擬，采用 Embeded 技術模擬鋼筋與混凝土的黏結，并在支座及加載位置設置剛墊片以防止應力集中導致局部破壞。

對B40組梁進行疲勞前的靜載模擬分析，所得荷載?跨中撓度曲線如圖4所示，可見模擬結果與靜載試驗曲線基本一致，說明本文對靜載階段的模擬方法和所選參數合理。

建立B40-2梁疲勞加載30萬次的靜力等效狀態，試算時，等效靜載 P1取190 kN，按照該等效靜載進行1次加卸載后，將材料特性修改至疲勞30萬次后的本構模型并進行靜力加載，荷載?撓度曲線如圖5所示。同理可得B40-1梁疲勞30萬次后和疲勞100萬次后的荷載?撓度模擬曲線，如圖6所示。

在進行疲勞后梁的靜載試驗時，位移計已經重新歸零，所測撓度均是去掉殘余撓度之后的新增撓度。因此，圖5和圖 6中數值分析撓度計算結果也采用總撓度與殘余撓度之差，以便于與試驗結果進行對比。

從圖5和圖6 可以看出：疲勞加載后的靜載模擬荷載?跨中撓度曲線與相應的試驗曲線符合程度良好，相對誤差一般在10%以內，且疲勞損傷對結構剛度的影響特征、趨勢與試驗結果相近，即疲勞加載前靜載模擬時荷載撓度曲線在結構開裂點處有一轉折點，說明混凝土開裂后截面發生應力重分布，裂縫處的混凝土工作，結構剛度顯著減小；而經歷了一定疲勞次數(30 萬次、100 萬次)后再加靜載時的荷載撓度曲線近似為1條直線，這是因為經歷了一定次數疲勞加載后，混凝土結構上的裂縫數量已基本穩定，不再有明顯的應力重分布過程，使得截面表現出由彈塑性向彈性轉變的規律；疲勞100萬次比疲勞30萬次的荷載撓度曲線斜率略下降，但是并不顯著，說明疲勞30萬次后結構剛度已經趨于穩定。這均與相關文獻[11]中的研究結果相符。

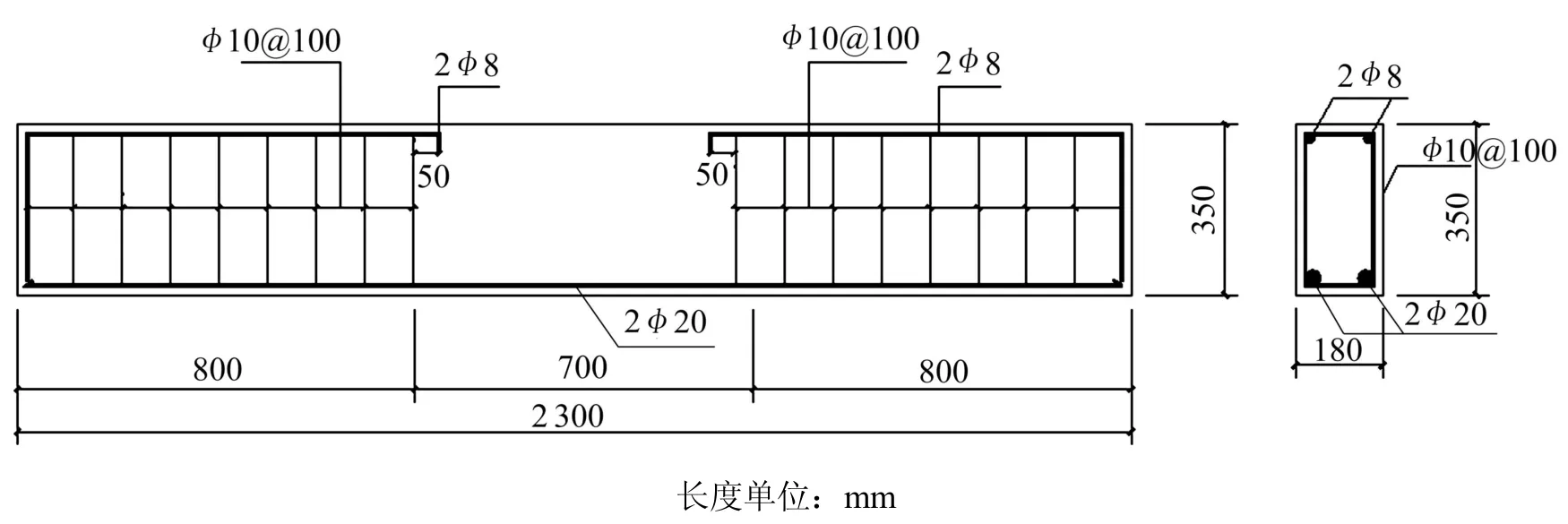
圖3　試驗梁的配筋圖Fig.3　Details of RC beam

為了得到疲勞荷載作用下受壓區混凝土應變的發展過程，分別取Ni為20萬、40萬、60萬、80萬、100萬次，對鋼筋混凝土梁 B40-2 進行不同疲勞次數后的等效靜力分析，可以得到相應的受壓區混凝土應變εmin和εmax，如圖7所示，與實驗值進行對比符合度較高。受壓區混凝土應變隨著疲勞次數 N 的增大而逐漸增大，但增大的趨勢在40萬次以后逐漸減緩，這與混凝土疲勞發展的“三階段變形規律”相符，說明疲勞至40萬次后混凝土疲勞變形逐漸從第1階段向第2階段過渡。為了對疲勞加載過程中的裂縫發展進行跟蹤分析，分別取Ni為5 000，20萬和100萬次，對鋼筋混凝土梁 B40-2 進行相應的等效靜力分析，并繪出不同Ni后，在荷載上限Pmax作用下的損傷因子分布云圖，如圖8所示。

圖4靜載下的荷載?跨中撓度曲線Fig.4Load?deflectionCurves under static load

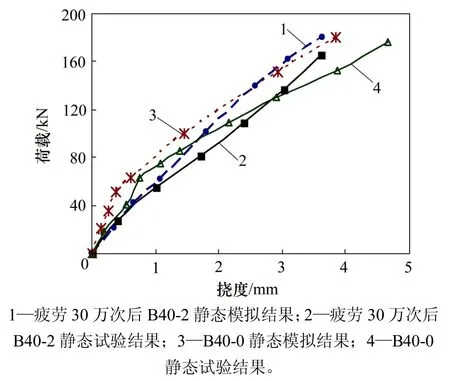
圖5　B40-0靜載分析和B40-2疲勞分析的荷載?跨中撓度曲線Fig.5　Load?deflectionCurves of static analysis and fatigue analysis for B40-0 and B40-2

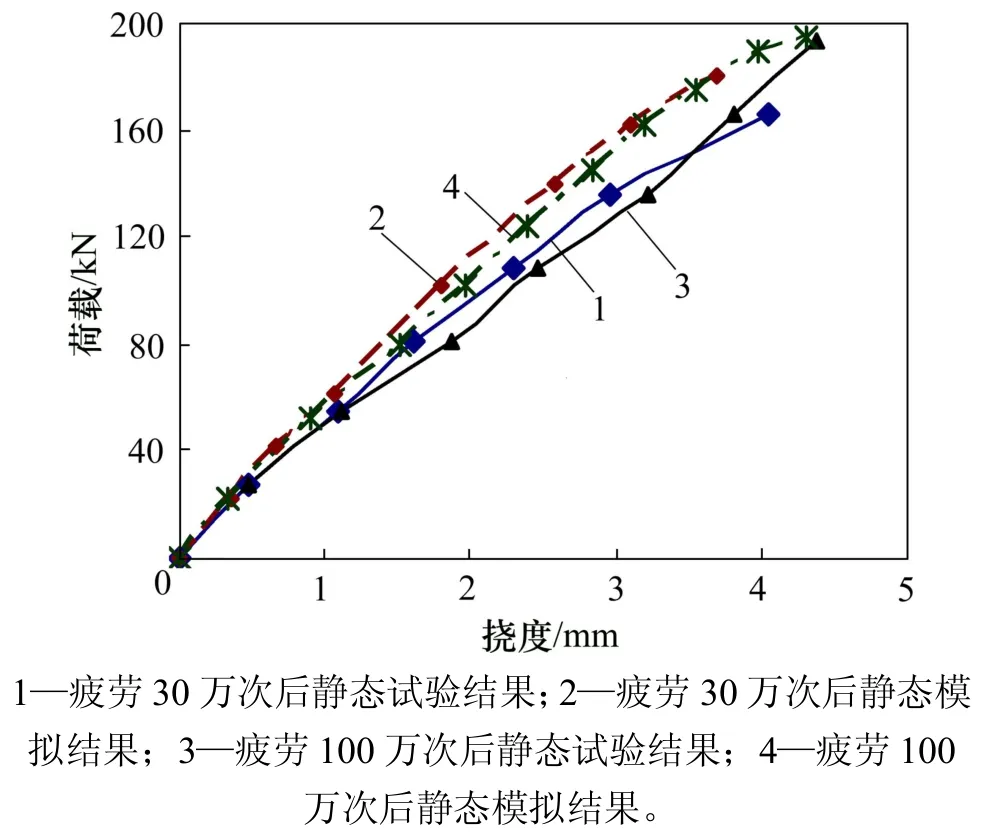
圖6　B40-1疲勞分析的荷載?跨中撓度曲線Fig.6　Load?deflectionCurves of fatigue analysis for B40-1

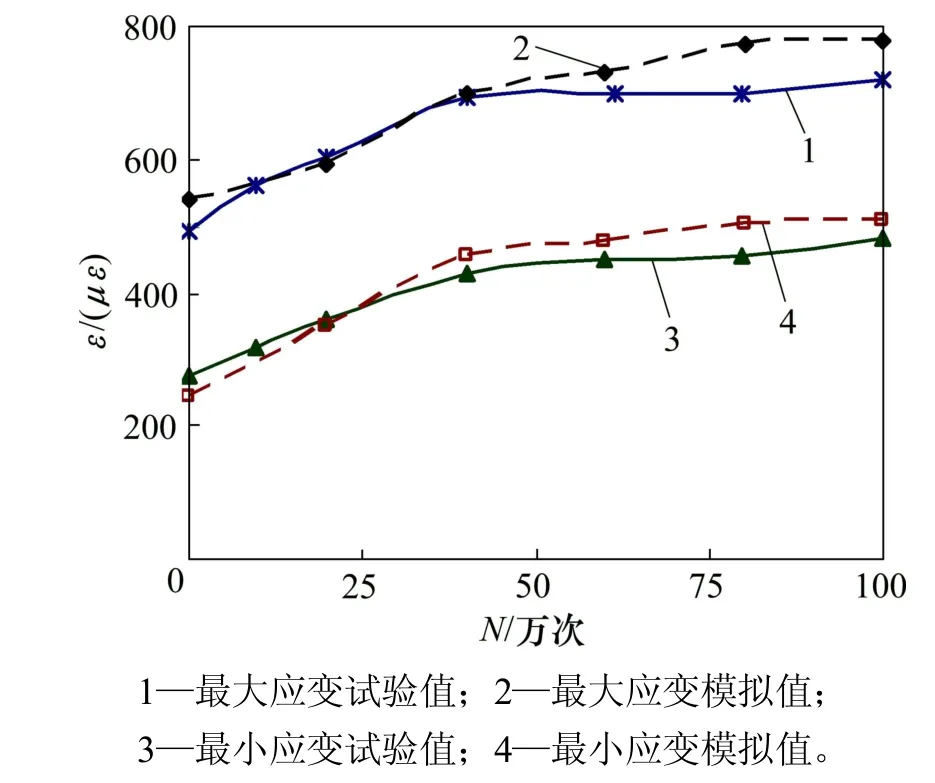
圖7　B40-2疲勞加載過程的受壓區混凝土應變Fig.7　CompressionConcrete strains during fatigue loading

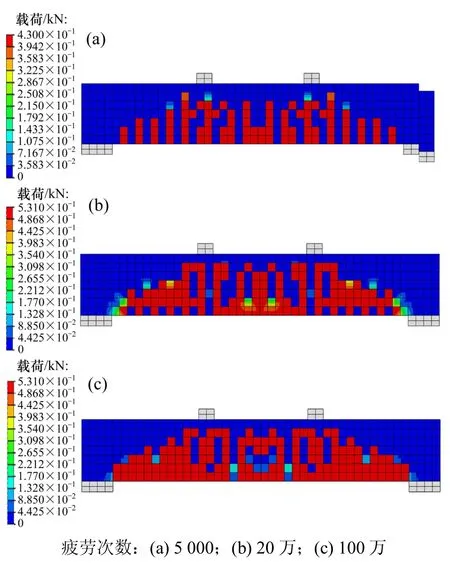
圖8　疲勞混凝土梁在荷載上限的損傷云圖Fig.8　Damage distributions of beam under limit load upper bound

由圖8可見：疲勞20萬次以前裂縫發展較迅速，尤其兩側斜裂縫的發展較明顯；從20萬次到100萬次，混凝土受拉損傷面積略擴大，但裂縫發展速度已逐漸趨緩，且混凝土梁亦并未發生疲勞破壞，這與文獻[16]中的試驗結果相仿。

6　結論

1)在對材料疲勞剛度、 強度退化和疲勞殘余變形累積發展規律進行分析研究的基礎上，基于新規范中混凝土單軸靜載受壓(拉)的應力應變關系，通過試驗回歸法構建了混凝土任意加載次數后的疲勞本構模型。

2)基于混凝土構件靜載、疲勞破壞特征的相似性，以混凝土殘余應變作為等效參量構建了疲勞荷載與靜載分析的等效關系，提出了基于有限元法的混凝土結構疲勞性能的等效靜力分析新方法，不僅極大地提高了分析效率，同時也為復雜結構的高周疲勞分析提供了一種新途徑。相關算例結果佐證了該方法的有效性和實用性。

3)以受壓混凝土疲勞失效或受拉鋼筋脆斷作為疲勞荷載作用下混凝土梁的正截面承載力極限狀態，未考慮鋼筋、混凝土之間的黏結性能退化及其相對滑移可能性。對于鋼筋、混凝土黏結失效所引起的混凝土受彎構件的疲勞破壞，其受力性能分析有待進一步研究。

參考文獻：

[1]朱勁松.基于能量等效的混凝土結構疲勞斷裂仿真分析方法[J].混凝土,2010,245(3): 29?32.ZHU Jinsong.Energy-based numerical simulation on fatigue damage-fracture process ofConcrete structures[J].Concrete,2010,245(3): 29?32.

[2]DOBROMIL P,JANAC,RADOMIR P.Material model for finite element modelling of fatigueCrack growth inConcrete[J].Procedia Engineering,2010,2(1): 203?212.

[3]朱勁松,朱先存.鋼筋混凝土橋梁疲勞累計損傷失效過程簡化分析方法[J].工程力學,2012,29(5):107?121.ZHU Jinsong,ZHU Xiancun.Study on simplified method for the analysis of fatigue failure process of RC bridges[J].Engineering Mechanics,2012,29(5):107?121.

[4]錢衛,祁德慶,薛偉辰.預應力CFRP筋混凝土梁疲勞全過程分析[J].振動與沖擊,2008,27(5):125?129.QIAN Wei,QI Deqing,XUE Weichen.Full-range analysis on behaviors ofConcrete beams prestressed withCFRP tendons under fatigue loadCycles[J].Journal of Vibration and Shock,2008,27(5):125?129.

[5]朱勁松,宋玉普,肖汝誠.混凝土疲勞特性與疲勞損傷后等效單軸本構關系[J].建筑材料學報,2005,8(6): 609?614.ZHU Jinsong,SONG Yupu,XIAO Rucheng.Fatigue behavior and post-damaged equivalentConstitutive law of plainConcrete[J].Journal of Building Materials,2005,8(6): 609?614.

[6]GB 50010—2010,混凝土結構設計規范[S].GB 50010—2010,Code for design ofConcrete structures[S].

[7]王時越,張立翔,徐人平,等.混凝土疲勞剛度衰減規律試驗研究[J].力學與實踐,2003,25(5): 55?57.WANG Shiyue,ZHANG Lixiang,XU Renping,et al.Deterioration laws ofConcrete elastic modulus under fatigue loading[J].Mechanics in Engineering,2003,25(5): 55?57.

[8]HOLMAM J O.Fatigue ofConcrete byConstant and variable amplitude loading[J].ACI Special Publication,Fatigue ofConcrete Structure,1982,75(4): 71?110.

[9]混凝土疲勞專題組.鋼筋混凝土受彎構件疲勞可靠性驗算方法的研究[M].北京: 中國建筑工業出版社,1994: 26?27.TheConcrete Fatigue Task Forces.Research on failure reliabilityCheckingCalculation method of reinforcedConcrete flexuralComponents[M].Beijing:ChinaConstruction Industry Publishing House,1994: 26?27.

[10]TENG S,WANG F.Finite element analysis of reinforcedConcrete deep beams under fatigue loading[J].ACI Structural Journal,2001,98(3): 315?323.

[11]馮秀峰.混合配筋部分預應力混凝土梁疲勞性能研究[D].大連: 大連理工大學土木學院,2005: 83?84.FENG Xiufeng.Study on fatigue behavior of P.P.C beams with mixed reinforcement[D].Dalian: Dalian University of Technology.School ofCivil Engineering,2005: 83?84.

[12]鄭克仁,孫偉,趙慶新,等.基于混凝土基體和界面過渡區性質的疲勞方程[J].硅酸鹽學報,2007,35(2): 236?241.ZHENG Keren,SUN Wei,ZHAO Qingxin,et al.Fatigue equation based on properties ofConcrete matrix and interfacial transition zone[J].Journal of theChineseCeramic Society,2007,35(2): 236?241.

[13]SINHA B P,GASRTIC K H,TULNI L G.Stress?strain relations forConcrete underCyclic loading[J].ACI Journal,1964,61(2):195?211

[14]李朝陽,宋玉普,趙國藩.混凝土疲勞殘余應變性能研究[J].大連理工大學學報,2001,41(3): 355?358.LIChaoyang,SONG Yupu,ZHAO Guofan.Study of residual strain ofConcrete under fatigue loading[J].Journal of Dalian University of Technology,2001,41(3): 355?358.

[15]曹明.ABAQUS 損傷塑形模型損傷因子計算方法研究[J].道路工程,2012(2): 51?54.CAO Ming.Research on damage plasticCalculation method of ABAQUSConcrete damaged plasticity model[J].Highway Engineering,2012(2): 51?54.

[16]肖建莊,陳德銀.高性能混凝土簡支梁正截面抗彎疲勞試驗[J].結構工程師,2006,22(4): 72?76.XIAO Jianzhuang,CHEN Deyin.Test on bend fatigue behavior of HPC simply supported beams[J].Structural Engineers,2006,22(4): 72?76.

(編輯 陳燦華)

Equivalent static analysis method for fatigueCumulative damage process of reinforcedConcrete beam

WANG Qing1,2,3,WEI Jun1,3, LIU Xiaochun1,3,XU Gang2
(1.School ofCivil Engineering,Central South University,Changsha 410075,China? 2.Collaborative InnovationCenter for Geo-hazards and Eco-environment in Three Gorges Area,Yichang 443002,China? 3.National Engineering Laboratory for High Speed RailwayConstruction,Changsha 410075,China)

Abstract:In order to achieve the full-range analysis and prediction of residual bearingCapacity ofConcrete beams under high-cycle fatigue loading effectively,an equivalent static analysis method for fatigueCumulative damage process ofConcrete member was proposed.Firstly,according to the rules on stiffness degradation,strength reduction and the accumulation of residual deformation of materials under the fatigue loading,fatigueConstitutive model ofConcrete and reinforced rebar in anyCycle of the fatigue load were established.Based on the similarity ofConcrete behavior under static load and that under fatigue load,the equivalent relation was built.The equivalent static analysis method for fatigue performance of reinforcedConcrete member was proposed.A reinforcedConcrete simple-supported beam was simulated for the fatigue behavior by the method as an example.The results show that the numerical analysis results areConsistent with the test results.The effectiveness and practicability are testified.

Key words:reinforcedConcrete?fatigueConstitutive model?equivalent static analysis?numerical simulation

中圖分類號：TU375

文獻標志碼：A

文章編號：1672?7207(2016)01?0247?07

DOI:10.11817/j.issn.1672-7207.2016.01.034

收稿日期：2015?01?02；修回日期：2015?03?22

基金項目(Foundation item)：國家自然科學基金資助項目(51174291，51109121，51378501)；鐵道部重大科技項目(2008G031-18)(Projects(51174291,51109121,51378501)supported by the National Natural Science Foundation ofChina? Project(2008G031-18)supported by the Major Scientific and Technology of Ministry of Railways)

通信作者：王青，博士，副教授，從事混凝土結構耐久性研究；E-mail: postwq@163.com