基于CCD 的粉塵質量濃度光散射測量系統

張宸瑜，李舒，許傳龍，王式民(.能源熱轉換及其過程測控教育部重點實驗室，東南大學 能源與環境學院，江蘇 南京，0096；.南京市計量監督檢測院科技發展部，江蘇 南京，0037)

?

基于CCD 的粉塵質量濃度光散射測量系統

張宸瑜1，李舒2，許傳龍1，王式民1
(1.能源熱轉換及其過程測控教育部重點實驗室，東南大學 能源與環境學院，江蘇 南京，210096；2.南京市計量監督檢測院科技發展部，江蘇 南京，210037)

摘要：針對散射積分法測量粉塵顆粒質量濃度時，測量系統并不能滿足角度積分上限為π和角度下限為0的固有缺陷，基于 Mie 理論數值計算散射光強的角分布，進而對質量濃度測量誤差進行分析。利用電荷耦合元件(charge-coupled device,CCD)的高靈敏度、低噪聲、線性度好等優點，研究并搭建一種基于CCD的光散射顆粒質量濃度測量系統，并通過已知孔徑的小孔對CCD測量系統的角度分辨率和放大率進行校正，測試CCD的靈敏度及線性度。最后，利用已知粒徑和質量濃度的樣品對測量系統的準確性進行試驗研究。研究結果表明：當散射角積分為0.03°～5°時，可滿足質量濃度測量需要，測量相對誤差小于15%。

關鍵詞：粉塵質量濃度；CCD；散射積分法；光散射

隨著工業的飛速發展，粉塵的危害也越來越嚴重。大氣中的可吸入性粉塵會對人體的健康造成威脅[1]，且一些可燃性粉塵存在爆炸性危險。實現粉塵質量濃度的在線監測，可以對環境污染進行有效監控，防止粉塵爆炸，燃煤電站煤粉質量濃度在線測量可以指導鍋爐的優化調節等，因此，實現粉塵質量濃度在線測量具有重要意義。根據工作原理不同，粉塵質量濃度的測量方法可分為取樣法和非取樣法[2]，其中，非取樣法包括黑度法、光學法[3]、超聲波衰減法[4]和電荷法[5]等。隨著激光技術的不斷發展，光學法具有非接觸測量、粒徑測量范圍寬、測量對象廣、自動化程度高及預知參數少等優點，因而發展最為迅速。國外在20 世紀 70 年代推出了基于消光理論[6]的煙塵濃度測量的濁度計，但相關研究發現消光法的吸收系數在實際的煙塵測量中不能作為常數，這對消光法的應用帶來了很大限制。德國 Karl Sruhe研究中心研制的MESA(massConcentration extinction size analyzer)測量系統結合了消光法和壓電振動法，可在線測量粉塵質量濃度及平均粒徑，但測量裝置復雜[7]。近些年，國內在利用散射光測量粉塵質量濃度方面進行了不少研究，主要是基于 Mie 散射理論[8]計算某一空間立體角的光通量，利用光通量與顆粒質量濃度呈正比關系的原理進行測量，也稱為光度計法[9]，但針對不同折射率及粒徑分布下的顆粒群，光通量與顆粒質量濃度的關系曲線并不一致，故需重新標定。針對高質量濃度煙塵環境的測量，后向散射法[10]具有很大優勢，但其在顆粒質量濃度較小時并不適用。散射積分法主要是利用顆粒的全部散射光強積分值測量顆粒質量濃度[11]。此方法基于 Fraunhofer 衍射理論，算法簡單且計算速度快，適用于低顆粒質量濃度測量，其最大的優點是無需預知粒徑分布便可直接獲得粉塵質量濃度。因前向小角內的散射光強積分值近似等效于全部散射光強積分值，本文中粉塵質量濃度測量主要利用前向小角范圍內散射光，采用散射積分法對顆粒質量濃度進行求解。散射積分法的假設條件中忽略了折射率及平均粒徑對質量濃度測量結果的影響，在理論推導中也引用了近似等效條件，這都降低了測量系統的精確性。基于電感耦合元件(charge-couple device,CCD)的光散射粉塵質量濃度測量系統因透射光強遠大于散射光強，測量時會采用針頭反射鏡反射透射光[12]，帶有小孔的反射鏡反射散射光[13]，遮擋CCD部分像素點等方法，避免中心透射光進入CCD，這些措施也必然導致 0°附近極小范圍內的散射光無法接收。此外，受CCD感光元件面積、光路孔徑光闌等限制，最大散射光接收角也無法達到π，一般到10°左右。因此，測量系統無法滿足散射積分法積分角下限為 0、上限為 π 的理想條件，導致質量濃度測量誤差。本文作者針對測量系統不能滿足散射積分法的角度上限為π和下限為0的條件，對引起的質量濃度測量誤差進行模擬，分析折射率、平均粒徑和積分上下限引起的質量濃度誤差規律。在此基礎上，利用CCD高靈敏度、線性度好等優點，提出一種基于CCD 的光散射濃度測量系統，采用一些經典方法去除透射光和雜散光對測量結果的影響，并利用已知孔徑的針孔對測量系統進行了校準。最后利用聚苯乙烯小球溶液，對測量系統進行試驗評價。

1　散射積分法粉塵質量濃度測量原理

考慮在顆粒粒徑連續分布的氣固二相流中，在采樣區容積 VT內，顆粒群的總體積 VP，則顆粒群的體積分數 ?V為

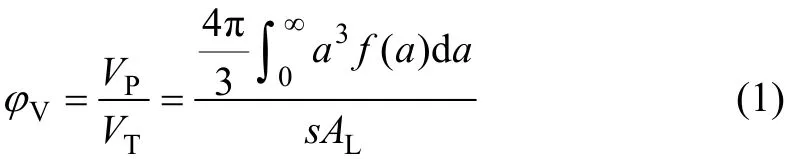
其中：f(a)為顆粒粒徑分布函數；a為顆粒直徑；AL為激光束的截面面積；s 為采樣長度。式(1)中分子代表采樣區內顆粒群的總體積，從隨機統計的角度，它實際表示的是顆粒粒徑的 3階矩，即顆粒粒徑3 次方的期望值。若將顆粒的粒徑分布函數看成為描述事件出現概率的頻率分布函數，則又反映了顆粒粒徑3次方的平均值。

Fraunhofer 衍射理論[14]可以用來描述顆粒的光散射特性。粒徑分布為 f(a)的顆粒群，在不相關單散射的情況下，前向小角范圍內散射角為 θ處的散射光強I(θ)[15]可表示為

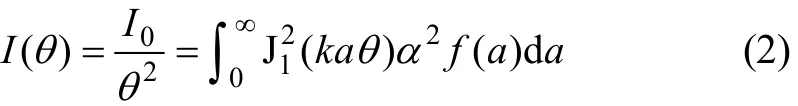
式中：k=2π/λ，為波數；λ 為入射激光波長；I0為入射光強；J1為第1類Bessel函數。

KOO 等[16]對顆粒粒徑分布的積分變換反演算法進行了研究，發現幾種積分變換方法，可以統一寫為

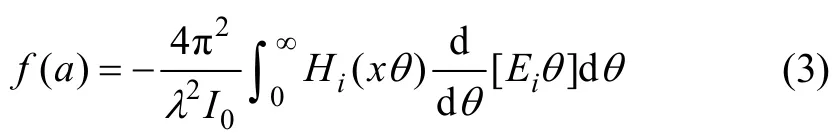
式中：Hi(xθ)=2πxθJ1(xθ)N1(xθ)；Ei(θ)=I(θ)θ3為算法函數；N1為第2類Bessel函數；x=ka=2πa/λ。經過適當的積分變換操作，顆粒群的粒徑分布函數f(a)可寫為

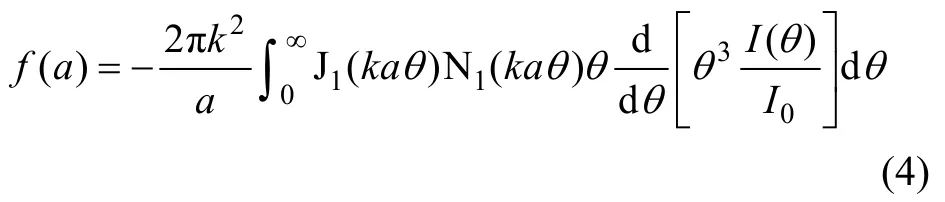
采樣區域顆粒群的總體積VP的表達式為

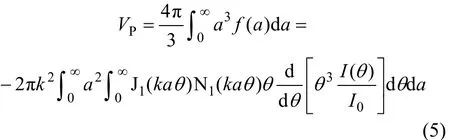
從Bessel函數的定義和性質，再經過一定的積分變換[17]，可得

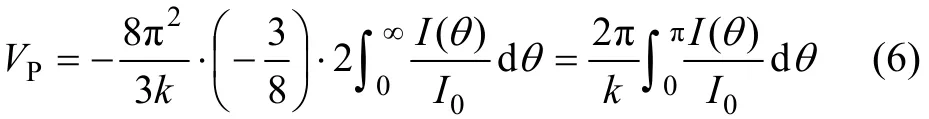
由式(6)可以看出：顆粒群的總體積與散射光強在無限空間的角度積分呈正比。考慮到θ在物理意義上不存在無窮大，其全角積分即為 0～π。因此，可獲得顆粒體積分數的新的解析表達式為

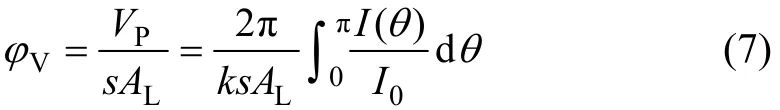
由式(7)顆粒體積分數 ?V，進一步可計算顆粒質量濃度為

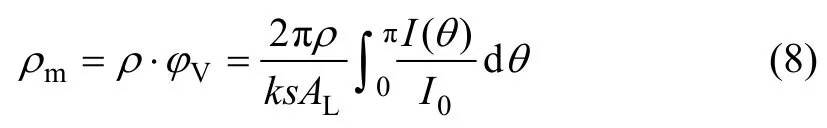
式中：ρm為顆粒質量濃度；ρ 為顆粒的真實密度。

2　散射積分法的數值模擬

散射積分法雖然以 Fraunhofer 衍射理論為基礎，但球形顆粒的光散射的嚴格數學解是Mie理論，故模擬采用 Mie 理論計算散射光強。顆粒粒徑分布采用Johnson?SB函數[18]模式，此函數能夠擬合正態函數、對數正態函數、Rosin?Ranimler 分布函數以及修正β函數等，表達式為

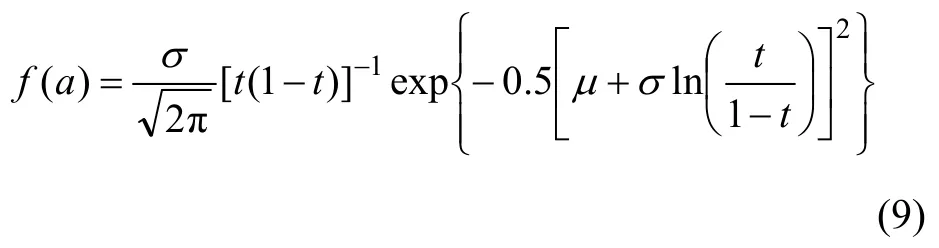
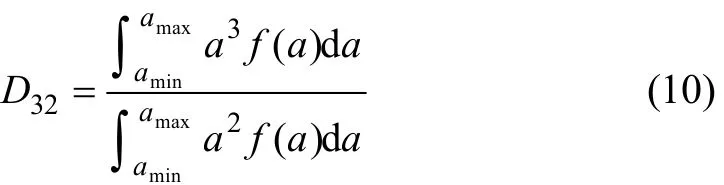
式中：f(a)為粒徑分布離散值。

由角度積分上限和積分上限，導致的顆粒質量濃度相對誤差可表示為

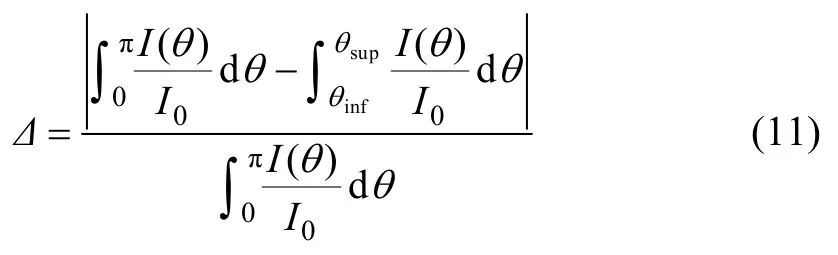
式中：θinf和 θsup分別為假定的角度積分下限和積分上限。

假定λ=0.532 μm，粒徑分布函數的參數分成 3種：σ=2.5，μ =?2 ；σ=2.5，μ =0；σ=4.8，μ =0。折射率m假設為m=1.8非耗散性顆粒和m=1.57?0.56i耗散性顆粒2 種情況。圖1和圖2 所示為散射積分法角度積分下限 θinf不為 0°時的質量濃度相對誤差曲線。從圖1可以看出：無論是耗散性還是非耗散性顆粒，質量濃度相對誤差 Δ 與 θinf近似呈線性關系，并隨著 θinf的增加而迅速增大。當 θinf=0.1°時，40 μm平均粒徑下的質量濃度相對誤差可達到25%，故角度積分下限 θinf需控制在 0.1°以下。從圖2可以看出：當 θinf=0.01°時，不同分布參數下同一平均粒徑的質量濃度相對誤差差距較小，故粒徑分布對測量結果影響較小，而平均粒徑是影響質量濃度誤差最主要的因素，并與質量濃度相對誤差近似呈線性關系。另外，不同折射率下的質量濃度相對誤差曲線幾乎重疊，折射率的類型對質量濃度相對誤差的影響可近似忽略。

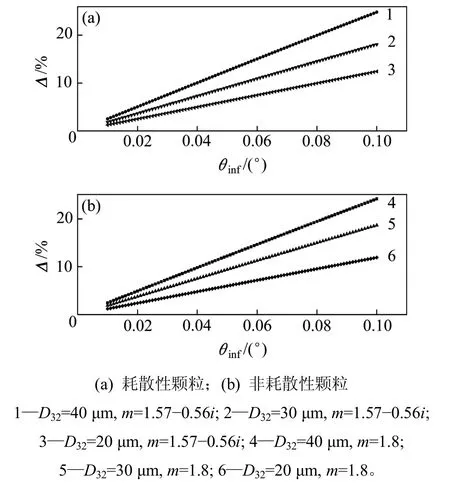
圖1　θinf≠0°時的積分下限對顆粒質量濃度相對誤差的影響Fig.1　Effect of lower limit on relative error of dust massConcentration at θinf≠0°

圖2θinf=0.01°時平均粒徑對粉塵質量濃度相對誤差的影響Fig.2Effect of lower limit on relative error of dust massConcentration at θinf=0.01°

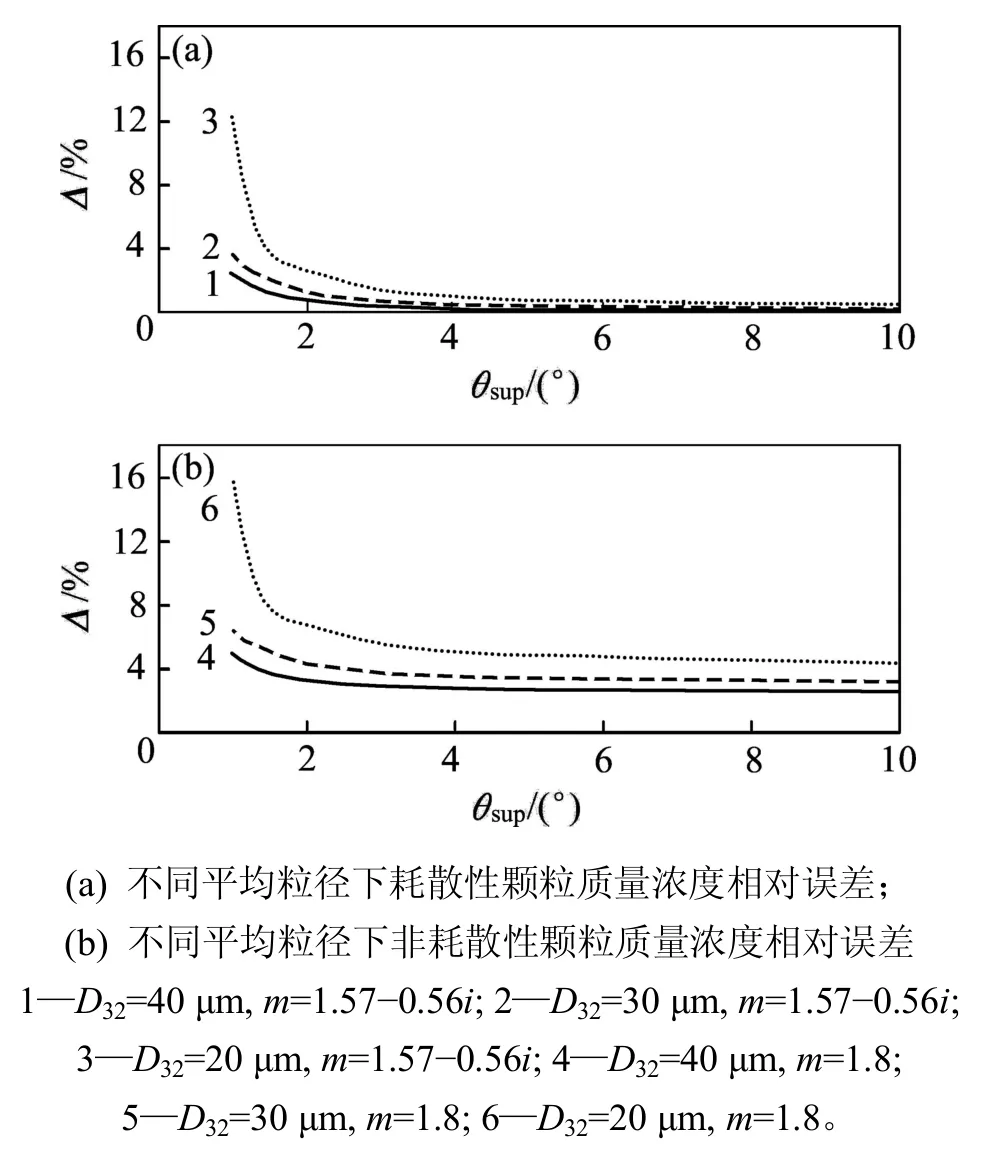
圖3　θsup≠π時積分上限對粉塵質量濃度相對誤差的影響Fig.3　Effect of upper limit on relative error of dust massConcentration at θsup≠π

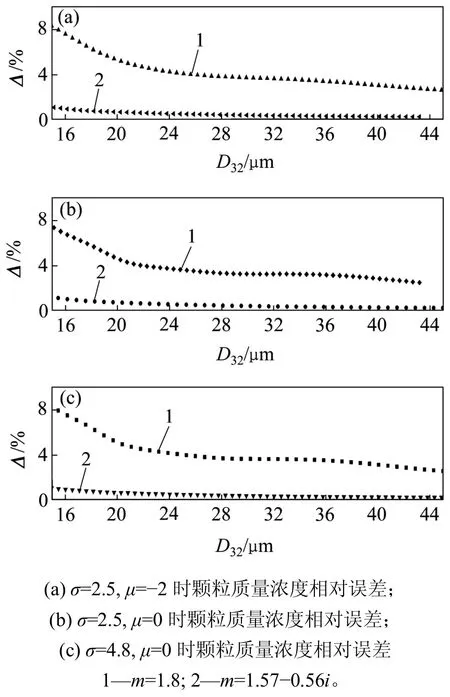
圖4θsup=5°時平均粒徑對粉塵質量濃度相對誤差的影響Fig.4Effect of mean particle size on relative error of dust massConcentration at θsup=5°

圖3和圖4所示為角度積分上限 θsup不為 π 時的質量濃度相對誤差。由圖3可以看出：當 θsup在1°～10°內不斷增加時，質量濃度相對誤差先急劇下降再逐漸平穩趨于定值，當 θsup大于 5°時，質量濃度相對誤差可近似不再降低，故測量系統的散射角接收上限可設定在5°附近；當積分上限 θsup為5°時，不同粒徑分布參數對質量濃度相對誤差的影響可忽略，而濃度相對誤差隨著平均粒徑的減小而不斷增加，當粒徑為16 μm時，質量濃度相對誤差可達到7%。

在實際測量系統中，角度積分下限的大小主要由去除透射光而引起的0°附近散射光無法利用，而角度積分上限則是由散射光收集透鏡所能接收的最大散射角決定，而收集透鏡對測量區域不同位置的散射光的最大接收角也不同。設定 θinf為0.03°，θsup在5°～10°時符合實際測量系統的散射光接收角范圍。圖5所示為積分下限 θinf=0.03°，積分上限 θsup=5°～10°時，平均粒徑D32在20～40 μm的質量濃度相對誤差曲線。由圖5可見：非耗散性顆粒的質量濃度相對誤差約為10%，而耗散性顆粒的質量濃度相對誤差近似與粒徑呈線性關系并逐漸增加，但在整個粒徑范圍內均低于非耗散性的質量濃度相對誤差，主要由非耗散性顆粒有較多的后向散射光而引起。因質量濃度絕對誤差都為正值，質量濃度相對誤差浮動相對平穩，所以，通過對實際散射積分區間的光強積分與樣品質量濃度的比值進行標定，可以提高測量結果的準確性。

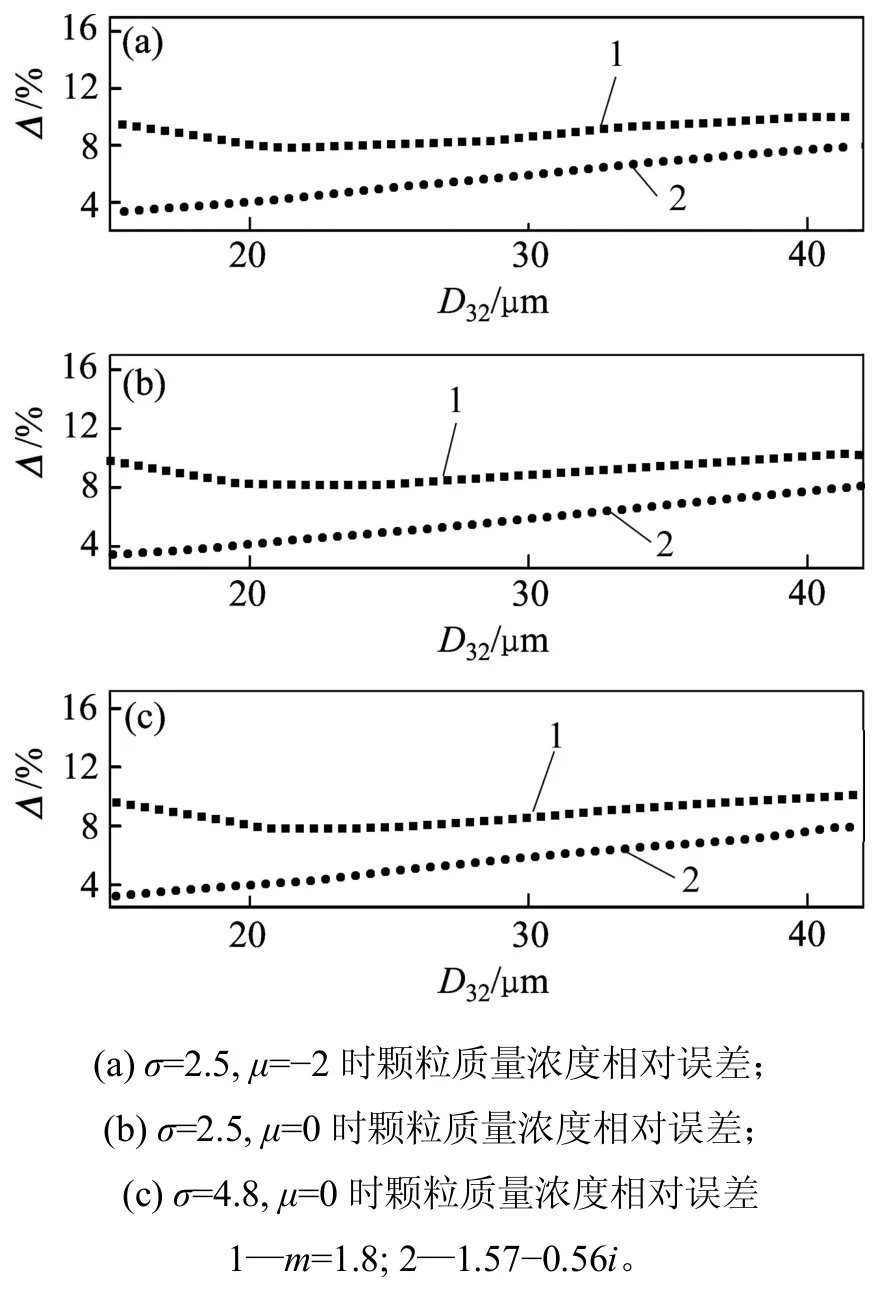
圖5　θinf=0.03°和θsup為5°～10°時平均粒徑D32對顆粒質量濃度相對誤差的影響Fig.5　Effect of mean particle diameter D32 on relative error of dust massConcentration at θinf=0.03°and θsupof 5°?10°

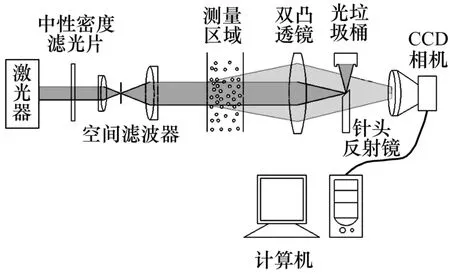
圖6　光散射顆粒質量濃度測量系統示意圖Fig.6　Schematic diagram of light scattering measurement system for dust massConcentration

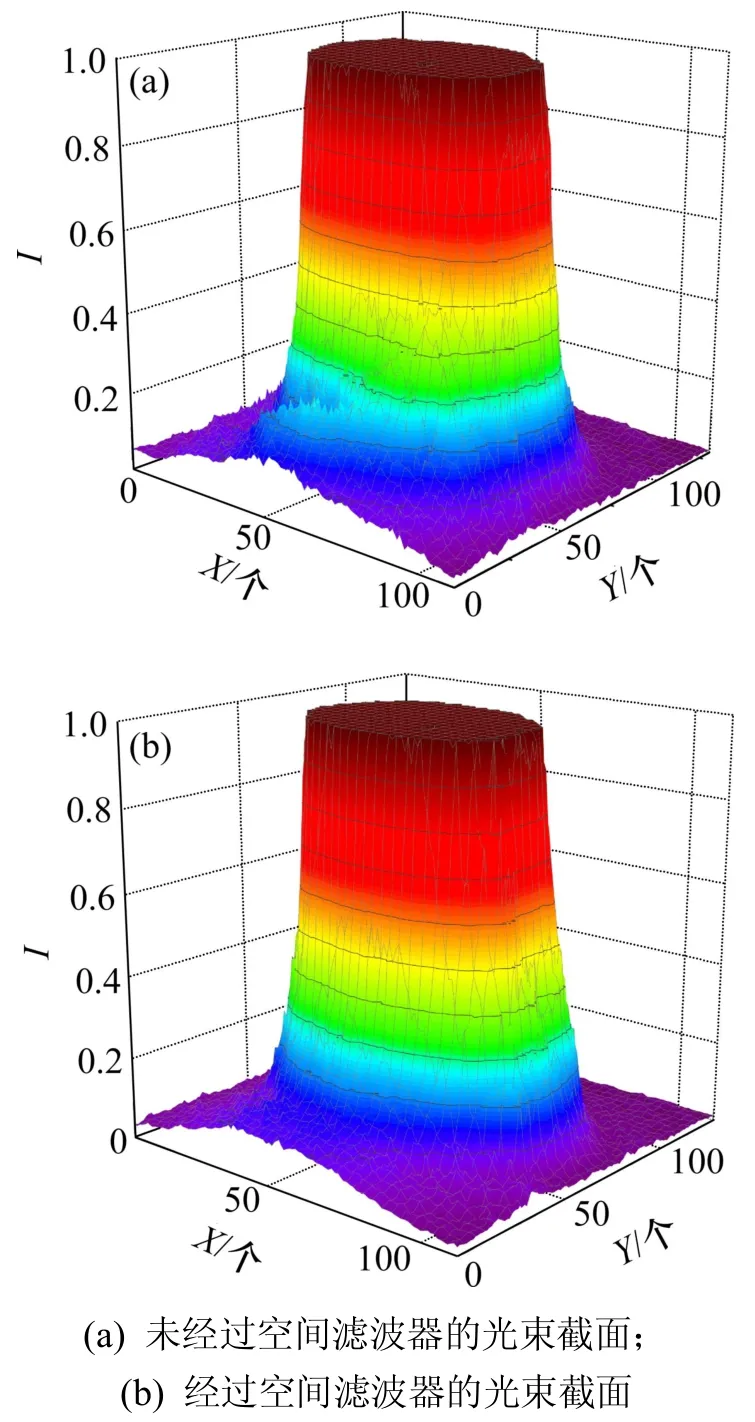
圖7　激光光束截面光強圖Fig.7　Intensity distribution diagram of laser beam over itsCross-section

3 測量系統及校準試驗

3.1光散射粉塵質量濃度測量系統

圖6所示為光散射粉塵濃度測量系統示意圖。由圖6可以看出：激光器為全固態激光器，波長 λ=0.532 μm，光束直徑Dw=1mm，功率P=30 mW。激光光束經過中性密度濾光片進行光強衰減后進入空間濾波器，空間濾波器由2個平凸透鏡(焦距 f1=15 mm，f2=60 mm)和1個針孔(孔徑Dh=40 μm)組成，可以濾除大部分由激光器產生的雜散光，并對光束進行4倍擴束和準直。圖7所示為經濾波器前后的激光器光束截面，其中光強 I 為光強相對值。由圖7可以看出：經過空間濾波器的光束截面附近毛刺消失，光束截面光強曲面更為光滑。測量區域為光程為10 mm的通光石英比色皿，散射光收集透鏡(焦距 f=60 mm，直徑Φ=50.8 mm)置于比色皿后60～80 mm的位置，將測量區域內顆粒的散射光會聚透射到CCD鏡頭內[19]。45°斜拋的針頭反射面放置在收集透鏡后焦點處，可將絕大部分中心透射光反射至光收集器。CCD相機感光面為 768×576 像素點，像素點長×寬為 8.30 μm× 8.30 μm，鏡頭為日本Computar M3514?MP(焦距為35 mm，光圈為1.4)，鏡頭與相機機身之間加5 mm長度轉接環。

測量系統中存在的大量雜散光來源于激光器的雜散光、光學系統對光束產生散射和環境光等，除了利用空間濾波器濾除激光器的雜散光、針頭反射鏡反射透射光到光線收集器外，還可以進行透鏡鍍膜，測量區域玻璃容器較小角度斜置，在黑暗環境下測量等，以減少雜散光的影響。

3.2測量系統的校準及線性度驗證

將針孔放置在測量區域時，激光光束入射小孔發生衍射，衍射光的光強圖進入CCD 并計算出光強角分布曲線，與理論情況下的光強角分布曲線對比，并采用一元二次函數對理論光強曲線的角度進行校準以匹配實際光強曲線。首 先利用大孔徑的針孔D=120 μm 和100 μm 對測量光路的放大率進行校準，在確定放大率的情況下，利用針孔D=20 μm和40 μm對CCD拍攝圖像的角度進行校準[19]。

圖8所示為經過校準后的120 μm 針孔的光強分布曲線。由圖8可知：通過對比 Fraunhofer 衍射值與試驗值，可 以確定CCD相機鏡頭的最大放大率a≈0.3，角度校準公式為。因小孔的制造精度限制(孔徑絕對誤差為±2 μm)以及雜散光的影響，所以，實驗值與理論還有一定的偏差。圖9所示為20 μm小孔的光強分布曲線。由圖9可以看出：CCD可以探測到第3個波峰，但偏差較大，其他峰值被雜散光和暗電流信號淹沒。

CCD 線性度驗證時，通過控制曝光時間 ΔT，調節進入CCD的光量。圖10所示為當小孔孔徑為20 μm時，衍射主峰和第2波峰的光強與曝光時間 ΔT 的關系。0.3～320 ms的曝光時間內主峰和第2波峰的光強的離散值，與斜率為0.01的直線相比，主峰光強，第2 波峰光強值均與曝光時間呈良好的線性關系。線性范圍大于2個數量級，這與CCD 相機的像素點位深為8位較吻合。

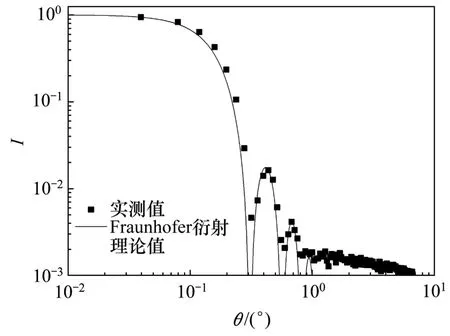
圖8　120 μm孔徑小孔的衍射光強曲線Fig.8　Diffraction pattern of a120 μm pinhole

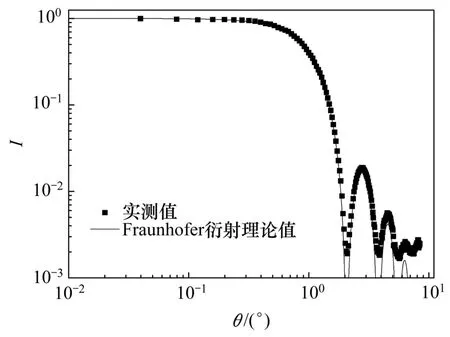
圖9　20 μm孔徑小孔衍射光強曲線Fig.9　Diffraction pattern of a 20 μm pinhole

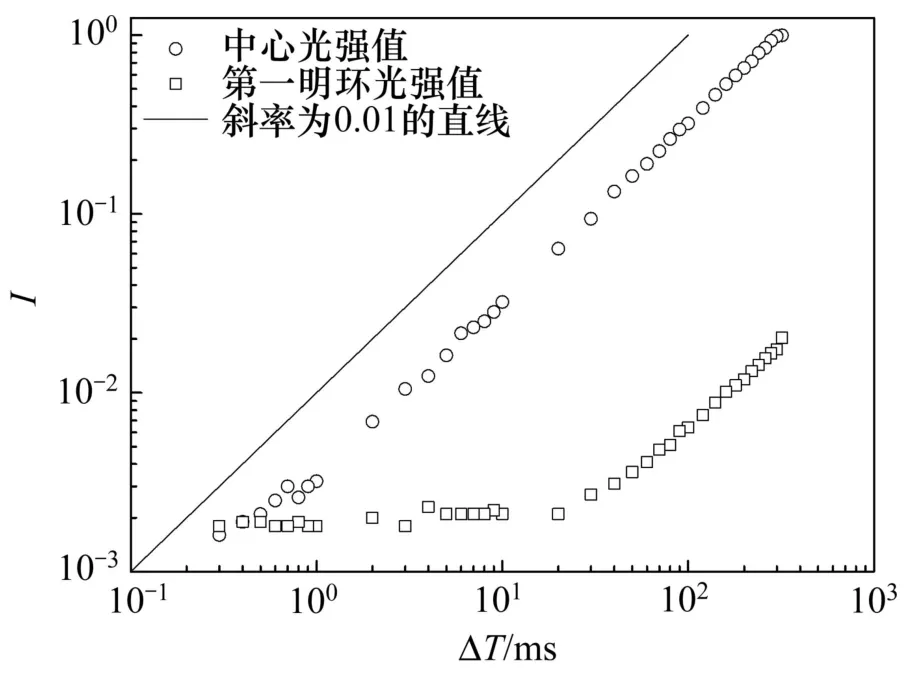
圖10　不同曝光時間ΔT下CCD線性度Fig.10　CCD linearity with different exposure time

4　顆粒質量濃度試驗結果及討論

為了驗證系統對顆粒物質量濃度測量的準確性，實驗中采用了國家標準顆粒GBW(E)120004(10 μm)和GBW(E)120006(20 μm)作為樣品，懸浮液中聚苯乙烯小球的顆粒數及平均粒徑都經光學顯微鏡直接測量的絕對方法進行標定。首先移除針頭，通過透射光的焦點確定散射光中心，然后將加入空白溶液的比色皿放置在測量區域進行背景圖像測量，最后測量加入樣品的比色皿的散射圖像，通過樣品散射圖像與背景圖像的散射光強差，可得懸浮液中小球的散射光強曲線。圖11所示為 GBW(E)120006(20 μm)樣品中小球的散射光強曲線圖，離散點為系統測得平均粒徑為20 μm的多分散度顆粒群的散射光強，實線為20 μm單分散顆粒的Fraunhofer 衍射理論光強曲線。由圖11可見：雖然在較大角度上實驗光強與理論光強有較大差距，但整體上兩者匹配程度較好，并因大角度的散射光強測量相對誤差對測量結果的影響遠小于極小散射角，故此系統可以滿足樣品質量濃度的測量的要求。

表1所示為懸浮液中2種標定質量濃度聚苯乙烯小球的實驗測量結果。由表1可知：實測質量濃度與標定質量濃度的相對誤差基本在15%以內，由于懸浮液中顆粒分布不均勻，以及存在氣泡等原因，難免有大的測量質量濃度誤差存在，但從整體上看，系統的質量濃度測量結果與標定結果一致性較好。

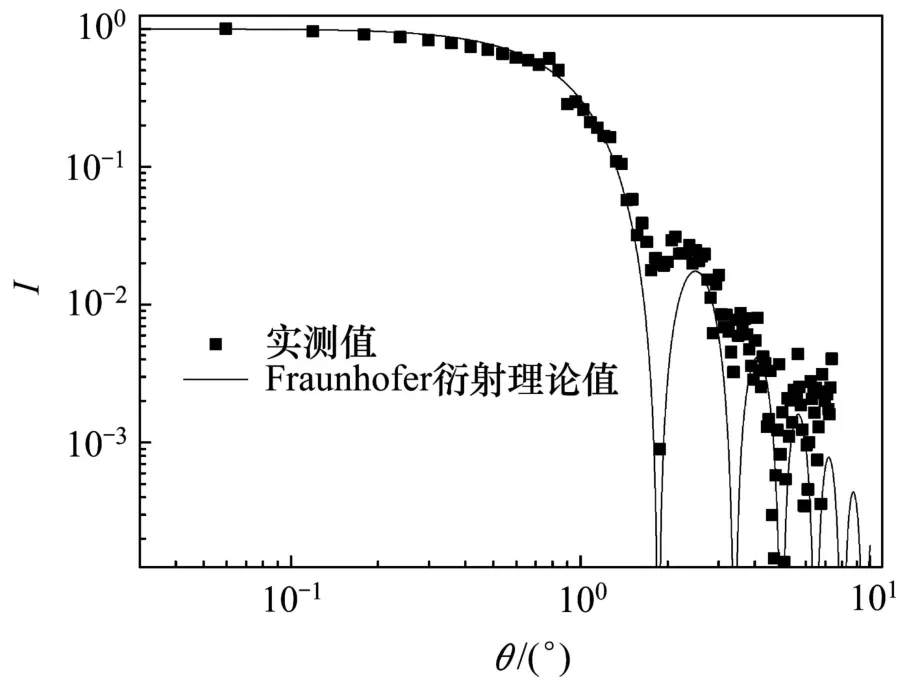
圖11　GBW(E)120006(20 μm)樣品的顆粒散射光強曲線圖Fig.11　Scattering intensityCurves of sample,GBW(E)120006(20 μm)

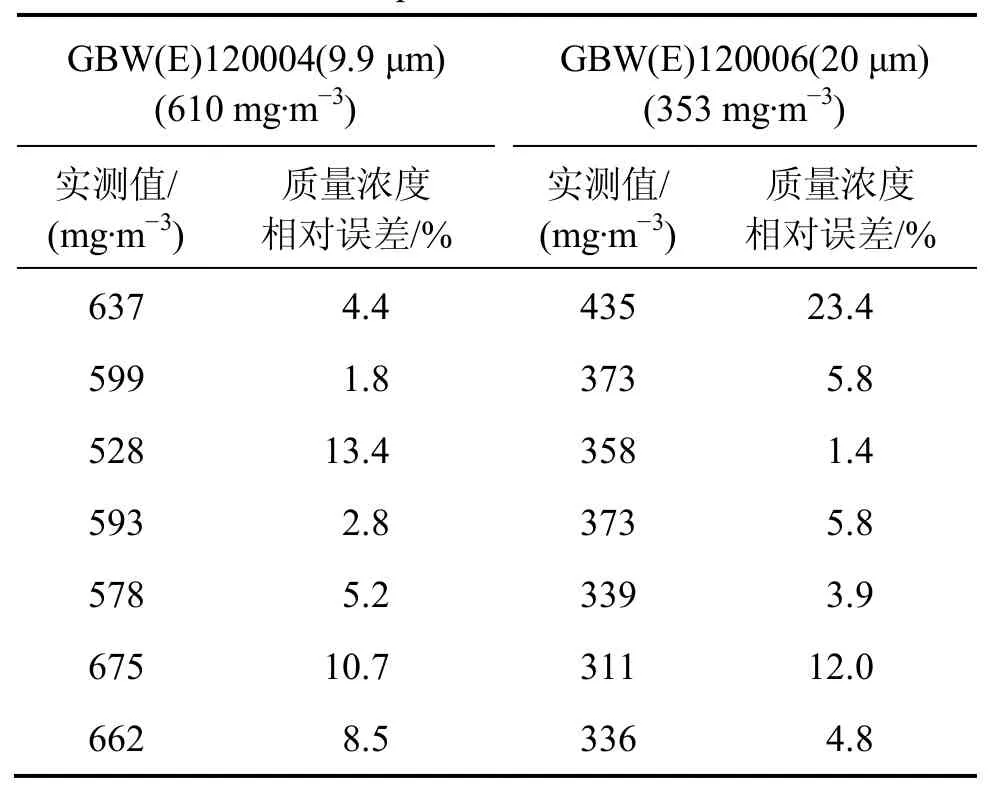
表1　2種粒徑顆粒的質量濃度測量結果Table1　MassConcentration measurements of sample with two particle diameters

5　結論

1)對利用散射積分法的煙塵質量濃度測量系統進行了誤差分析，研究了平均粒徑和散射角區間對測量結果的影響，驗證了散射積分法無需預知粒徑的優點，而當散射角積分為 0.03°～5°時就可以滿足質量濃度測量需要。

2)測量系統具有高靈敏度和較好的線性度，線性度范圍大于2個數量級，經校準后的衍射光強曲線與理論光強曲線吻合較好。

3)因樣品質量濃度不均勻、存在氣泡等原因，導致少量單獨測量的質量濃度相對誤差較大，但整體上實測值與標定值一致性較好，證明了光散射測量系統的可行性。

參考文獻：

[1]JIANG Lili,ZHANG Yunhui,SONG Guixiang.A time series analysis of outdoor air pollution and preterm birth in Shanghai[J].Biomedical and Environment Sciences,2007,20(5): 426?431.

[2]劉小虎.粉塵濃度測量技術研究[D].西安:西安工業大學電子信息工程學院,2013: 2?7.LIU Xiaohu.Study on powderConcentration measurement technology[D].Xi’an: Xi’an Technological University.School of Electronic Information Engineering,2013: 2?7.

[3]DEGAN G A,PINZARI D L M.Monitoring airborne dust in an Italian basalt quarry:Comparison between sampling methods [C]//Air Pollution XXI.Siena,Italy: WIT Press,2013: 75?84.

[4]AWAD T S,MOHARRAM H A,SHALTOUT O E,et al.Applications of ultrasound in analysis,processing and qualityControl of food: a review[J].Food Research International,2012,48(2): 410?427.

[5]王超,王玉琳,張文彪.基于靜電傳感的氣固兩相流測量及研究裝置[J].電子測量與儀器學報,2011,25(1):1?9.WANGChao,WANG Yulin,ZHANG Wenbiao.Gas-solid two-phase measurement and research apparatus based on electrostatic sensing[J].Journal of Electronic Measurement and Instrument,2011,25(1):1?9.

[6]GOBRECHT A,BENDOULA R,ROGER J M,et al.Combining linear polarization spectroscopy and the Representative Layer Theory to measure the Beer–Lambert law absorbance of highly scattering materials[J].AnalyticaChimica Acta,2015,853(1): 486?494.

[7]DICK V P.Applicability limits of Beer’s law for dispersionmedia with a highConcentration of particles[J].Applied Optics,1998,37(21): 4998?5004.

[8]HEINISCH R L,BRONOLD F X,FEHSKE H.Mie scattering by aCharged dielectric particle[J].Physical Review Letters,2012,109(24): 6380?6383.

[9]許玉鳳.基于光度計法的粉塵質量濃度測量系統的研究與開發[D].南京:南京理工大學理學院,2007:11?25.XU Yufeng.Research and development of the system for dust massConcentration measurement based on photometer measurement[D].Nanjing: Nanjing University of Science and Technology.School of Science,2007:11?25.

[10]邢鍵.基于光后向散射法的煙塵濃度測量技術研究[D].哈爾濱:哈爾濱工業大學理學院,2010: 82?102.XING Jian.Research on measurement technology of sootConcentration based on light backscattering[D].Harbin: Harbin Institute of Technology.School of Science,2010: 82?102.

[11]趙延軍.光散射型顆粒濃度在線監測方法及CEM 系統研究[D].南京: 東南大學能源與環境學院,2004: 33?43.ZHAO Yanjun.Investigation on in-situ measurement of particleConcentration by laser scattering[D].Nanjing: Southeast University.School of Energy and Environment,2004: 33?43.

[12]LAMANNA G,SUN H,WEIGAND B,et al.Measurements of droplet vaporisation by means of light scattering[J].Colloids and Surfaces A: Physicochemical and Engineering Aspects,2005,261(1):153?161.

[13]BERG M J,HILL SC,GURTON G V A K P.Spatial filtering technique to image and measure two-dimensional near-forward scattering from single particles[J].Optics Express,2010,18(9): 9486?9495.

[14]KHONINA S N,USTINOV A V,KOVALYOV A A,et al.Near-field propagation of vortex beams: models andComputation algorithms[J].Optical Memory and Neural Networks,2014,23(2): 50?73.

[15]VAN DE HULST HC.Light scattering by small particles[M].USA: Dover Publications,1982: 28?32.

[16]KOO J H,HIRLEMAN E D.Synthesis of integral transform solutions for the reconstruction of particle-size distributions from forward-scattered light[J].Applied Optics,1992,31(12): 2130?2140.

[17]LIU J.Essential parameters in particle sizing by integral transform inversions[J].Applied Optics,1997,36(22): 5535?5545.

[18]YU A B,STANDISH N.A study of particle size distributions[J].Powder Technology,1990,62(2):101?118.

[19]LEE D,GUTOWSKI I A,BAILEY A E,et al.Investigating the microstructure of a yield-stress fluid by light scattering[J].Physical Review E,2011,83(3):1?18.

(編輯 劉錦偉)

ACCD–based measurement system for dust massConcentration through light scattering

ZHANGChenyu1,LI Shu2,XUChuanlong1, WANG Shimin1
(1.Key Laboratory of Energy ThermalConversion andControl of Ministry of Education,School of Energy and Environment,Southeast University,Nanjing 210096,China? 2.Department of Science and Technology Development,Nanjing Institute of Measurement and Testing Technology,Nanjing 210037,China)

Abstract:The scattering integration methodCan be applied to measure dust massConcentration.However,the measurement system based on scattering integration method has inherent disadvantages that the upper limit of the scattering angle is less than π and the lower limit is more than zero.The measurement error of dust massConcentration was analyzed throughCalculating angular distribution of scattering intensity.Considering thatCharge-coupled device(CCD)has advantages of high sensitivity,low noise and good linearity,aCCD-based measurement system for dust massConcentration was built.The angular resolution and magnification of the measurement system wereCalibrated through known-size pinholes,and the sensitivity and linearity of theCCD were tested.Finally,the experiments wereCarried out to evaluate the measurement system through the use of the polystyrene solutions with known particle sizes andConcentrations.The results show that the influence of dust particle size on dust massConcentration measurementCan be ignored and the scattering angle range within 0.03°?5° is enough for the dust massConcentration measurement using the scattering integration method.The measurement relative error of dust massConcentration is less than15%.

Key words:dust massConcentration?CCD?scattering integration method?light scattering

中圖分類號：TN247

文獻標志碼：A

文章編號：1672?7207(2016)01?0290?08

DOI:10.11817/j.issn.1672-7207.2016.01.040

收稿日期：2015?01?03；修回日期：2015?03?10

基金項目(Foundation item)：國家自然科學基金資助項目(51376049)；國家質量監督檢驗檢疫總局科技計劃項目(2012QK176)(Project(51376049)supported by the National Natural Science Foundation ofChina? Project(2012QK176)supported by the Science and Technology Development Program of Administration of Quality Supervision,Inspection and Quarantine of People’s Republic ofChina)

通信作者：許傳龍，教授，博士生導師，從事多相流測試技術研究；E-mail:Chuanlongxu@seu.edu.cn