基于改進SFLA-PF算法的OFDM系統目標跟蹤

曹向東，毛永毅

(西安郵電大學 電子工程學院， 陜西 西安710061)

基于改進SFLA-PF算法的OFDM系統目標跟蹤

曹向東，毛永毅

(西安郵電大學 電子工程學院， 陜西 西安710061)

摘要:在OFDM通信系統中，為了解決非線性的目標跟蹤問題,提出了基于改進混合蛙跳算法(SFLA)和粒子濾波算法(PF)相結合的方法來研究動態目標跟蹤技術。首先利用高斯變異的局部搜索能力強和柯西變異的全局搜索能力強等優點對混合蛙跳算法進行改進，然后用改進后的混合蛙跳算法來優化粒子濾波算法進行動態跟蹤，其優點不需要重采樣步驟，有效地保持了粒子的多樣性和有效性。仿真結果表明，該算法能夠有效實現動態目標跟蹤，并且跟蹤效果優于同等條件下的混合蛙跳算法和粒子濾波算法。

關鍵詞:OFDM；混合蛙跳；粒子濾波；高斯變異；柯西變異

在軍事以及民用領域中,尋求可靠而又精確的目標位置一直是動態跟蹤技術研究的主要目的。因此對于動態目標跟蹤的研究引起了國內外很多學者的高度重視[1]。同時基于常規的卡爾曼濾波算法通常要求系統是線性高斯型的,所以不能直接用來解決非線性等問題。于是文獻[2]提到基于粒子濾波的目標跟蹤，主要針對粒子濾波的動態模型與觀測模型進行研究，并將圖像分割與隨機森林分類器引入粒子濾波跟蹤算法之中，來提高跟蹤性能。文獻[3]提出了粒子濾波優化目標跟蹤算法，這種方法是基于PFTMT算法與模板匹配算法跟蹤精度高的優點相結合來提高粒子濾波跟蹤精度；文獻[4]提出基于粒子群和M-H粒子抽樣粒子濾波的跟蹤技術研究，它主要采用分布式結構，抑制粒子退化現象，從而使粒子快速收斂，進而提高跟蹤精度；文獻[5]提出了基于群智能算法的動態目標跟蹤技術研究，利用智能算法中粒子個體間相互具有聯絡、通信的優良特性，將其融入到粒子濾波算法中進行跟蹤；文獻[6-7]改進群體智能算法，是通過增加變異因子的方法來提高混合蛙跳算法的搜索尋優性能。

本文介于粒子濾波算法本身個體與個體之間沒有交互性的性質，進而引入了個體與個體之間具有交互性和通信機制的蛙跳算法來優化粒子濾波算法，首先對蛙跳算法引入高斯變異和柯西變異，提高了算法收斂速度和引導個體快速跳出局部最優，再把改進的SFLA-PF算法運用在OFDM系統中進行動態目標跟蹤，驗證表明，該算法表現出很好的跟蹤效果。

1算法描述

1.1粒子濾波算法

粒子濾波(Particle Filter，PF)是從20世紀90年代開始發展起來用于解決目標跟蹤問題的新算法。也是目前解決非線性跟蹤問題的核心算法。

假設描述非線性系統的狀態方程為

xk=f(xk-1,uk-1),Zk=h(xk，vk)

(1)

貝葉斯估計是利用先驗概率分布函數來構造系統的后驗概率分布函數的基本思想，同時遞推過程也是由先驗概率來逼近后驗概率，假設此狀態下初始概率密度函數的表達式為

p(x0|z0)=p(x0)

(2)

則在此狀態下的預測方程為

p(xk|z1:k-1)=∫p(xk|xk-1)p(xk-1|z1:k-1)dxk-1

(3)

狀態的更新方程為

(4)

(5)

其中

(6)

(7)

1.2蛙跳算法

1.2.1基本的蛙跳算法

蛙跳算法(Shuffled Frog Leaping Algorithm，SFLA)于2003年由Eusuff和Lansey提出的為解決組合優化問題的智能算法。作為一種新型的仿生物學智能優化算法，該算法具有概念簡單、計算速度快、全局尋優能力強、易實現等優點，因此被廣泛用于解決工程領域里尋求最優解等問題。

在一個S維的目標尋優搜索空間里，讓隨機產生的N只青蛙個體組成初始群體p={x1,x2,…,xN},則第i只青蛙個體可以表示為xi=[xi1,xi2,…,xis]。

在初始種群生成之后，讓種群內的所有青蛙個體的適應值按照降序排列，同時把種群內部適應值最優的個體標記為xg；再將整個種群分成m個子群，同時每個子群中包含n個個體，并滿足關系N=m×n,設Mk為第k個子群的集合，分配過程如下

Mk={xk+m(l-1)∈p|1≤l≤n},1≤k≤m

(8)

然后把每一個子群中適應值最好和最差的個體分別標記為xb和xw，同時把整個種群中適應值最好的個體標記為xg，然后再對每個子群中的xw個體循環進行局部搜索，具體的更新策略方式如下

D=r·(xb-xw)

(9)

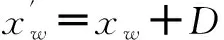
(10)

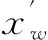
1.2.2改進的蛙跳算法

本文提出了改進蛙跳算法(SFLA)，一方面基于該算法在尋優過程中局部搜索能力較弱，引入了柯西變異，利用它的全局搜索能力，易引導個體跳出局部最優，避免了算法陷入局部最優的缺陷[8]，另一方面基于SFLA在尋優中容易陷入早熟收斂，引入了高斯變異，利用它較強的局部搜索能力，提高了該算法的收斂速度，很好地避免了發生早熟收斂的缺點[9]。兩種變異算子相互結合使用，提高了算法的尋優精度和收斂速度。

常用的變異算子有4種，包括高斯變異算子、柯西變異算子、混沌變異算子、levy變異算子等。本文為了避免SFLA算法陷入局部最優和發生早熟收斂現象，選用高斯變異和柯西變異。

高斯分布又稱為正態分布，是研究概率論等學科的一項重要分布函數。通常將高斯變異記為N(μ,σ2),μ為連續變量的期望，σ2為變量的標準方差。則概率密度函數為

(11)

高斯分布可記為

(12)

通過式(11)可以看出，高斯分布密度函數關于x=μ對稱，同時在x=μ時函數取得最大值，曲線呈現中間高兩邊低的正態分布趨勢。從方程中還可以看到，當μ=0，σ2=1時，稱此為標準高斯分布，記為N(0，1)

(13)

柯西分布通常表示為C(β，λ)，β和λ表示位置參數，概率密度函數可描述如下

(14)

其密度函數可表示為

(15)

從式(15)可以看出，曲線關于x=β對稱，當β=0，λ=1時，柯西分布記為C(0,1),此時被稱為標準柯西分布，其表達式為

(16)

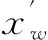
改進后的具體為

D=r·(xb-xw)

(17)

D=D+D·Ui

(18)

(19)

其中：Ui=(Ui1,Ui2,…,UiD)

1.3改進的SFLA-PF算法的動態目標跟蹤

介于粒子濾波本身個體不具有交互性，而混合蛙跳算法中個體具有交互性和相互聯絡的通信機制，所以將改進后性能優越的蛙跳算法融入到粒子濾波算法當中，讓粒子之間相互不再獨立，而具有合作共存的意識，并用于目標跟蹤。根據前面對兩種算法的具體介紹，可以得出改進SFLA-PF算法的具體實現步驟如下：

第3步：適應度值更新。按照式(6)計算種群中每個個體的適應度值。并用式(7)計算個體的適應度值標準化。

第4步：判斷子群。判斷當前種群中出現的最優個體是否與上次進化時得到的最優個體相同，如果相同子群在進行局部搜索時就采用柯西變異算子，如果不同，就選用高斯變異算子。

第5步： 更新目標狀態。對子群進行局部搜索，確定xg和xb的值。并采用式(17)、(18)和(19)更新方法對xw進行更新，重復此操作，直到子群都滿足收斂條件為止。

第7步：在OFDM系統中通過計算移動臺到達3個基站的TOA值，然后用TOA值得到TDOA的值。

第8步：利用上述得到的TDOA值結合改進的粒子濾波(SFLA-PF)算法實現對移動臺的位置估計，進而實現對動態目標的定位跟蹤。

2仿真及分析

2.1仿真條件

為了檢驗本文所提跟蹤算法的合理性以及該算法性能的優越性，將改進的SFLA-PF算法和PF算法應用到OFDM通信系統中進行跟蹤對比，并利用仿真軟件對這兩種跟蹤算法進行仿真分析。

算法仿真過程中采用典型的7小區組成的蜂窩結構,服從T1P1信道模型，服務基站BS1(0,0)位于小區中心,小區半徑為3 km,取粒子數N=100(經驗證為較優值)，移動臺由坐標(200，200)處出發,沿與x坐標軸正方向成60°的方向勻速運動，初速度為24 m/s，信噪比為30 dB。OFDM信號仿真參數：取載波數為128，采樣周期為50 ns，OFDM帶寬為20 MHz，天線單元數為6，天線間隔0.5 m。

2.2狀態描述

狀態方程表達式為

(20)

觀測方程表達式為

zk=h(xk)+nk=

(21)

位置的均方根誤差表達式如下

(22)

2.3仿真結果分析

圖1為本文算法、混合蛙跳算法和粒子濾波算法在以上條件下的動態目標跟蹤仿真圖，橫坐標表示移動臺沿x軸方向的運動距離，縱坐標表示沿y軸方向移動臺與基站的距離，從圖中可以看到本文算法跟蹤效果非常優越，跟蹤軌跡基本都緊靠真實運動軌跡，且跟蹤性能穩定，基本能夠準確估計目標真實運動狀態，相比之下，跟蹤效果明顯優于混合蛙跳算法和粒子濾波算法。以上也充分說明了本文改進算法提高了粒子間的合作共存能力，保持了粒子的多樣性和有效性，也很好地抑制了粒子退化等問題。

圖1　不同算法的跟蹤效果對比

圖2為本文算法、SFLA算法和粒子濾波算法獨立仿真的均方根誤差仿真圖，可以看出隨著仿真次數的增加，本文算法跟蹤性能較穩定，誤差保持在很小的范圍內波動，而SFLA算法和粒子濾波算法的誤差波動相對較大，且始終大于本文算法的跟蹤均方誤差，也充分說明了本文改進算法有效利用了蛙跳算法的很多優點，克服了粒子濾波算法中粒子退化現象等很多缺陷，表現出很好的跟蹤效果。

圖2　不同跟蹤算法的均方根誤差比較

算法的性能分析，從圖1、圖2可以看出， SFLA算法的跟蹤效果略優于粒子濾波算法，因為SFLA算法具有良好的蛙群更新機制，保持了蛙種類的多樣性，進而在跟蹤性能上較穩定，而粒子濾波算法本身的粒子更新機制較差，只保留了較好的粒子，導致種群內粒子多樣性缺失，進而導致跟蹤效果變差。而本文的改進算法恰好結合了兩個算法的優點，抑制了粒子的退化，從而保持了粒子的多樣性，所以跟蹤效果穩定而精確。同時，本文改進算法省去了粒子重采樣的步驟，大大降低了算法的復雜度。

3結論

綜上所述，本文提出了基于改進SFLA-PF算法的目標跟蹤技術，利用蛙跳算法的高效計算能力和優良的全局搜索能力，以及很好的信息交互和協作能力。把它引入到粒子濾波算法中，使其粒子群體也表現出復雜的智能效果，從實驗結果看這種改進很好地抑制了粒子陷入局部最優和退化現象，同時也驗證了該算法能夠精確地進行動態目標跟蹤。

參考文獻：

[1]PAULINER.Isaglobalsystemofinternationallarge-scaleassessmentsnecessaryfortrackingprogressofapost-2015learningtarget?[J].Compare:ajournalofcomparativeandinternationaleducation，2015，45(3)：486-490.

[2]宋策. 基于粒子濾波的目標跟蹤技術研究[D].長春：長春光學精密機械與物理研究所，2014.

[3]朱良誼，王慶. 一種基于粒子濾波的優化目標跟蹤算法研究[J].西北工業大學學報，2013(6)：967-973.

[4]蔣鵬,宋華華,林廣. 基于粒子群優化和M-H抽樣粒子濾波的傳感器網絡目標跟蹤方法[J].通信學報，2013(11)：8-17.

[5]馬勤. 基于群體智能算法的動態目標跟蹤技術研究[D]. 天津：天津理工大學,2010.

[6]葛宇，王學平，梁靜. 改進的混合蛙跳算法[J].計算機應用，2012(1)：234-237.

[7]DANILOP，MASSIMOT，PIERLUIGII.Improvingtheprofitabilityoftechnicalanalysisthroughintelligentalgorithms[J].Journalofinterdisciplinarymathematics，2013，16(2-03)：203-215.

[8]張友華.混合蛙跳算法的改進及其應用研究[D].蘭州：甘肅農業大學，2013.

[9]李晶晶,戴月明. 自適應混合變異的蛙跳算法[J]. 計算機工程與應用，2013(10)：58-61.

[10]蔡榮太,吳元昊,王明佳,等.視頻目標跟蹤算法綜述[J].電視技術，2010，34(12)：135-138.

[11]THANGNV，TRINHCD，TRANDT.ApplicationofstreettrackingalgorithminanINS/GPSintegratednavigationsystem[J].IEEEjournalofresearch，2015，61(3)：1-9.

[12]蔣巍,張健,曾浩. 基于智能視頻監控系統的運動目標檢測和跟蹤[J].電視技術，2012，36(5)：110-114.

[13]張彤,馬延柯,首照宇.一種改進的Mean-Shift實時車輛跟蹤算法[J].電視技術，2015，39(17)：126-130.

Improved tracking targets SFLA-PF algorithm based on OFDM system

CAO Xiangdong，MAO Yongyi

(SchoolofElectronicEngineering，Xi′anUniversityofPosts&Telecommunications，Xi′an710061，China)

Abstract:In the OFDM communication system, in order to solve nonlinear target tracking problem, an improved SFLA (SFLA) and particle filter (PF) is proposed based on a combination of methods to study the dynamic target tracking technology. Firstly, Gaussian mutation local search ability and Cauchy mutation global search ability, etc. are used to improve SFLA, then improved SFLA is used to optimize the dynamic tracking of particle filter algorithm, its advantages are not requiring resampling steps, and meanwhile effectively maintain the diversity and effectiveness of the particles. The simulation results show that the algorithm can effectively achieve dynamic target tracking, and tracking better than SFLA and particle filter algorithm under the same conditions.

Key words:OFDM；SFLA；particle filter；Gaussian mutation；Cauchy mutation

中圖分類號:TN929.53

文獻標志碼：A

DOI：10.16280/j.videoe.2016.03.022

基金項目：陜西省自然科學基金項目(2014JM2-6088)

作者簡介：

曹向東(1988— )，碩士，主研移動臺定位跟蹤技術；

毛永毅(1969— )，博士，教授，主研通信信號處理、移動臺定位跟蹤技術。

責任編輯：許盈

收稿日期：2015-11-26

文獻引用格式：曹向東，毛永毅.基于改進SFLA-PF算法的OFDM系統目標跟蹤[J].電視技術，2016，40(3)：103-106.

CAO X D，MAO Y Y. Improved tracking targets SFLA-PF algorithm based on OFDM system [J].Video engineering，2016，40(3)：103-106.