基于偏置輸出3-RRR+(S-P)球面并聯機構的仿生髖關節

楊亞敬　孫通帥　周玉林

燕山大學，秦皇島，066004

基于偏置輸出3-RRR+(S-P)球面并聯機構的仿生髖關節

楊亞敬孫通帥周玉林

燕山大學，秦皇島，066004

摘要：首先以偏置輸出的3-RRR+(S-P)仿生關節機構為原型機構，依據仿生原則并參照人體股骨結構，確定關節機構的偏置角。然后，提出關節機構工作空間與人體髖關節運動空間相協調的設計原則，進而確定關節機構的安裝定位角度，完成人形機器人髖關節設計；建立仿生關節空間與機構空間的映射關系，并對該髖關節的運動學正反解進行求解。最后，通過數值計算證明關節機構可實現人體基本運動，同時使用Xsens Technologies公司的可穿戴式完全無線3D身體慣性跟蹤儀及磁性運動跟蹤器，采集人體髖關節在實際運動狀態下的位姿信息，將獲取信息經映射關系轉換和反解變換，導入ADAMS模型中進行校驗，進一步驗證了建立的映射關系、安裝定位角度及正反解的正確性。

關鍵詞：偏置輸出；仿生學；髖關節球面；并聯機構

0引言

人形機器人是機器人領域最活躍的分支之一，其關節的結構和性能直接決定其整體性能，受到國內外學者的廣泛關注。人體肌肉群多以并聯驅動的形式來完成關節運動。

三自由度球面機構具有結構緊湊、靈活可靠等特點，可用于人體髖關節[1]、靈巧眼[2-3]等，實現空間三自由度的轉動。眾多學者對該機構進行了分析研究。Tao等[4]提出了一種基于增大機構工作空間和減少桿件之間干涉的系統設計方法，并依據此方法得到了3-RRR球面并聯機構的優化結果。楊加倫等[5]基于旋量理論計算，探討了正交三自由度球面機構位置正反解的方法，獲得了機構的雅可比矩陣，運用牛頓迭代法求解得到了3個被動角的數值解，利用指數積公式直觀地得到了該機構的位置正解。Saafi等[6]在對三自由度球面機構正運動學進行分析時，采用了冗余傳感器的方法，使運動學正解變得簡單化，控制精度也大大提高了。文獻[2-3,7-12]也對三自由度球面機構進行了相關研究。

另有眾多學者對髖關節也進行了深入研究。日本東京大學提出了一種雙球面髖關節運動單元，該運動單元采用雙球面作為機構原型，具有6個自由度[13]。程剛等[14-15]對3SPS+1PS并聯機構的設計和控制進行了分析，對機構的工作空間進行了優化，將此機構應用到人體髖關節，并制作了髖關節實物樣機。

侯雨雷等[1]以3-RRR三自由度球面并聯機構為原型，在其靜力學及剛度特性分析基礎之上，從仿生學角度出發，通過植入中心球面副的方式，提出可應用于人形機器人髖關節的3-RRR+(S-P)球面并聯機構，實現了靜力卸載及剛度均衡。

目前的研究都是對球面機構進行運動學、動力學分析，鮮有將其與人體構型結合，基于仿生關節分析進行關節設計。本文則從仿生學角度出發，通過確定機構偏置角度和安裝定位角度，將偏置輸出3-RRR+(S-P)球面并聯機構[16]應用于人體髖關節，給出仿生關節空間與機構空間的映射關系，求解基于偏置輸出3-RRR+(S-P)球面并聯機構仿生髖關節的運動學正反解。在此基礎上，對本機構模型進行數值驗證和具體人體髖關節信息采集分析，進一步說明本文分析結果的正確性和仿生關節的應用價值。

1仿生髖關節空間與人體空間的協調性

人體髖關節的結構屬于傳統被動球面鉸鏈結構，但是其運動空間明顯大于傳統被動球面鉸鏈的工作空間[16-17]。研究人體髖關節結構發現，人體股骨與傳統被動球面鉸鏈的輸出桿有明顯不同：股骨整體呈彎拐狀，股骨頸與股骨體夾角為55°～62°，如圖1所示。同時，人體髖關節的運動范圍也存在一定規律性，表1所示為醫學統計數據。

圖1　人體股骨結構

運動關節關節運動范圍度量位置角度(°)髖關節冠狀面(oymzm)內擺動95矢狀面(oxmzm)內擺動165繞大腿軸旋轉65

人體髖關節在運動過程中各個角度間存在耦合，關系十分復雜，為近似獲得人體髖關節的運動空間，基于上述數據，同時假定髖關節各個關節運動角度間相互獨立，則可獲得人體髖關節最大運動空間的形狀，如圖2所示。

(a)整體形狀(b)俯視形狀圖2　人體髖關節最大運動空間形狀

依據仿生設計原則，為使仿生髖關節工作空間包含或等于人體髖關節空間，達到最優仿生效果，將偏置輸出3-RRR+(S-P)球面并聯機構應用于仿生髖關節，其輸出桿軸線向任意方向偏折，釋放輸出桿繞z軸的轉動對機構輸出的影響，從而擴大機構的工作空間。

偏置輸出的3-RRR+(S-P)仿生關節機構如圖3所示。偏置輸出桿軸線與直輸出桿軸線的夾角稱為偏擺角αh。偏置輸出桿的末端點P與球心的連線OP是實際輸出桿軸線，OP的長度定義為Lt，它與直輸出桿軸線的夾角稱為偏置角t,其表達式為

t=αh-arcsin(r0sinαh/Lt)

(1)

其中,αh為股骨骨干與股骨頸的夾角。在本仿生機構中，t為動平臺z軸與OP的夾角，αh為動平臺z軸與輸出桿軸線的夾角。

依據人體尺寸模型，機構球半徑r0取80mm、股骨頸長度取90mm，大腿(按身高1700mm設計)為473mm。則得到t的取值范圍約為46°～54°。

為便于分析，建立機構的結構參數和坐標系如下(圖3)：α1、α2、β1、β2、η1i、η2i(i=1,2,3)，球半徑R，其中，η1i(i=1,2,3)為zi1(i=1,2,3)與z11在下平臺的投影所成角度；η2i(i=1,2,3)為zi3(i=1,2,3)與z13在上平臺投影所成角度。zi1、zi2、zi3為過球心的三條轉動副軸線。選取機構的中心點O為坐標原點，建立固定坐標系{C}(Ox0y0z0)、動坐標系{D}(Oxyz)和偏置坐標系{P}(Ox1y1z1)。其中，固定坐標系與支撐桿固連，z0軸與支撐桿軸線重合，正向向上，x0軸由z0軸轉到z11軸及右手螺旋法則確定，y0軸由右手螺旋法則確定；動坐標系與輸出桿固連，z軸與直輸出桿軸線重合，正向指向外，x軸由z軸轉到z13軸及右手螺旋法則確定，y軸由右手螺旋法則確定；偏置坐標系與輸出桿固連，假定直輸出桿和偏置輸出桿所構成的平面與Ozy面重合，取OP為z1軸，正向向外，x1軸與x軸正向重合，y1軸由右手螺旋法則確定。

當t=0°時，偏置輸出的3-RRR+(S-P)仿生關節機構的安全工作空間的形狀及相對固定坐標系的位置如圖4所示。當46°≤t≤54°時，仿生關節機構的安全工作空間變大，其形狀及相對固定坐標系的位置如圖5所示。

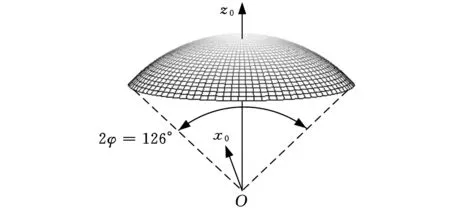
圖4　3-RRR+(S-P)球面并聯機構的安全工作空間

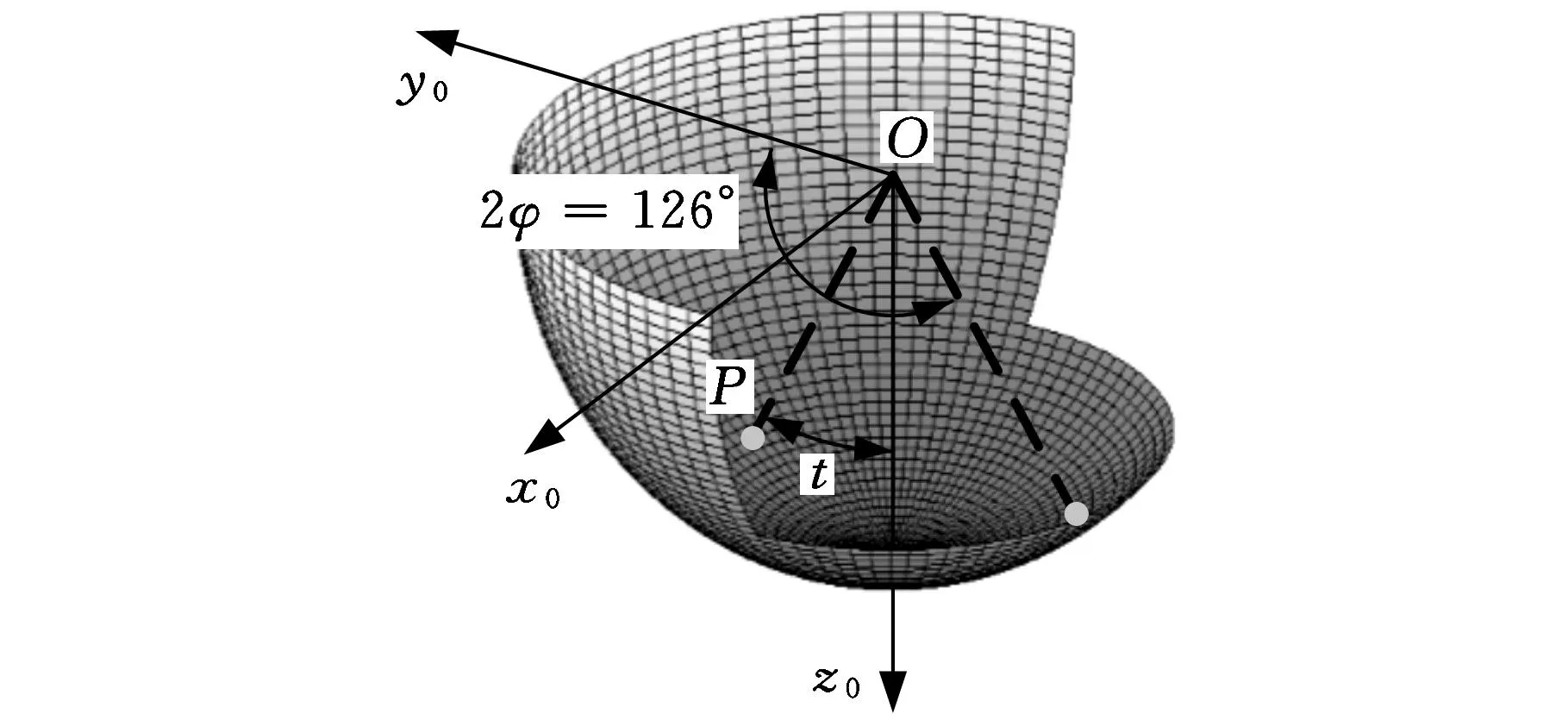
圖5　偏置輸出的3-RRR+(S-P)機構的安全工作空間

對比圖2與圖5不難發現，偏置輸出3-RRR+(S-P)球面并聯機構的安全工作空間可以完全覆蓋人體髖關節的最大運動空間，它完全可以滿足機構工作空間與人體髖關節運動空間的協調性要求。綜上，該偏置輸出3-RRR+(S-P)球面并聯機構滿足仿生運動要求，可應用于仿生髖關節。

2安裝定位角度與空間映射關系

2.1安裝定位角度α0、β0、γ0

經研究人體骨盆和髖關節的實際結構發現，髖關節的髖臼的中心線并不是位于球窩的中心位置，而是向前下方傾斜的，與各個平面均存在一定的夾角：髖臼中心射線與水平面成30°～40°的夾角，與冠狀面之間的夾角呈30°～40°。股骨在矢狀面內運動范圍較大(-45°～120°)，人體髖關節球窩的特點是中性線與水平面存在夾角，男性比較大，約為22°～30°，女性的約為20°～25°，如圖6所示，同時，(無論男女)其中性線均向前偏轉約12°～20°(與冠狀面夾角)。股骨結構如圖1所示，股骨骨干呈彎拐形狀向兩側伸出，股骨頸與股骨骨干夾角約50°～60°[18]。

在進行仿人髖關節設計時，需考慮髖關節應如何擺放安裝，使機構的工作空間(輸出桿運動范圍)與人的肢體運動范圍相協調，兩個空間的中心區域重合或機構的工作空間覆蓋肢體運動空間。因此按照人體特征，以及仿生關節機構工作空間的對稱特性，為確定安裝位置，本文提出了基準坐標系相對過渡坐標系安裝定位角：α0、β0、γ0，下標“0”表示髖關節。

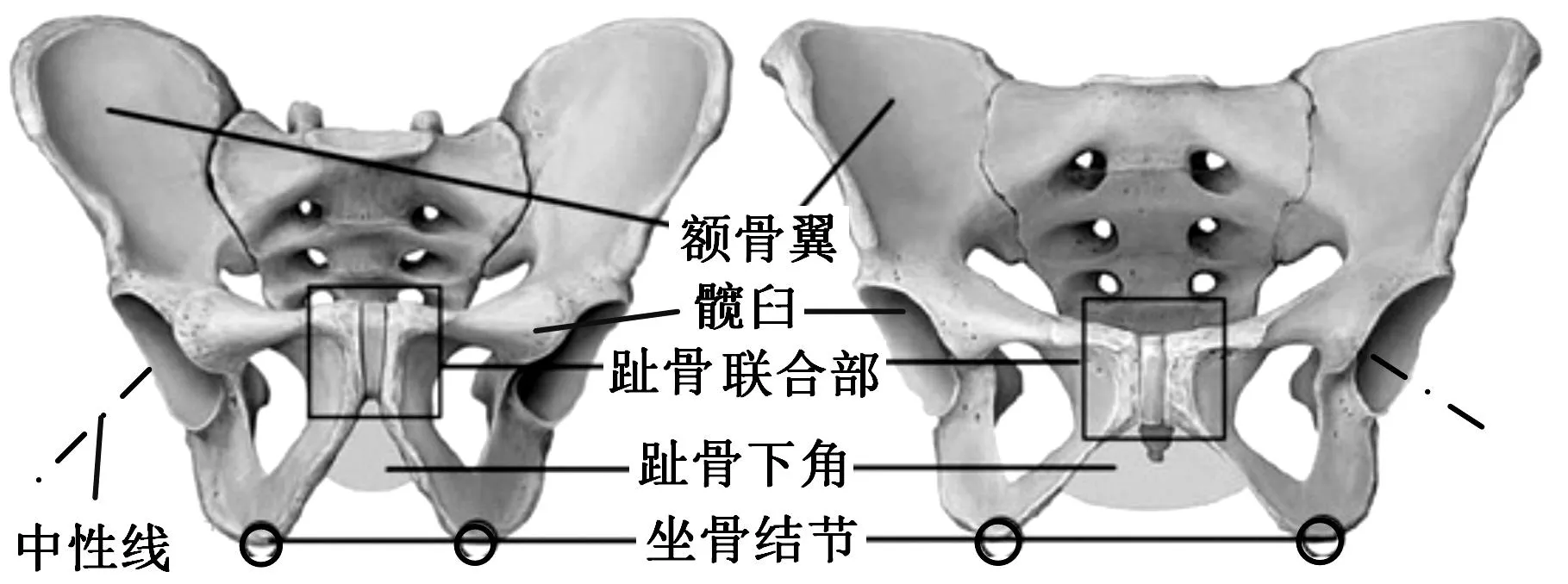
(a)男性骨盆(b)女性骨盆圖6　人體骨盆結構

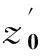
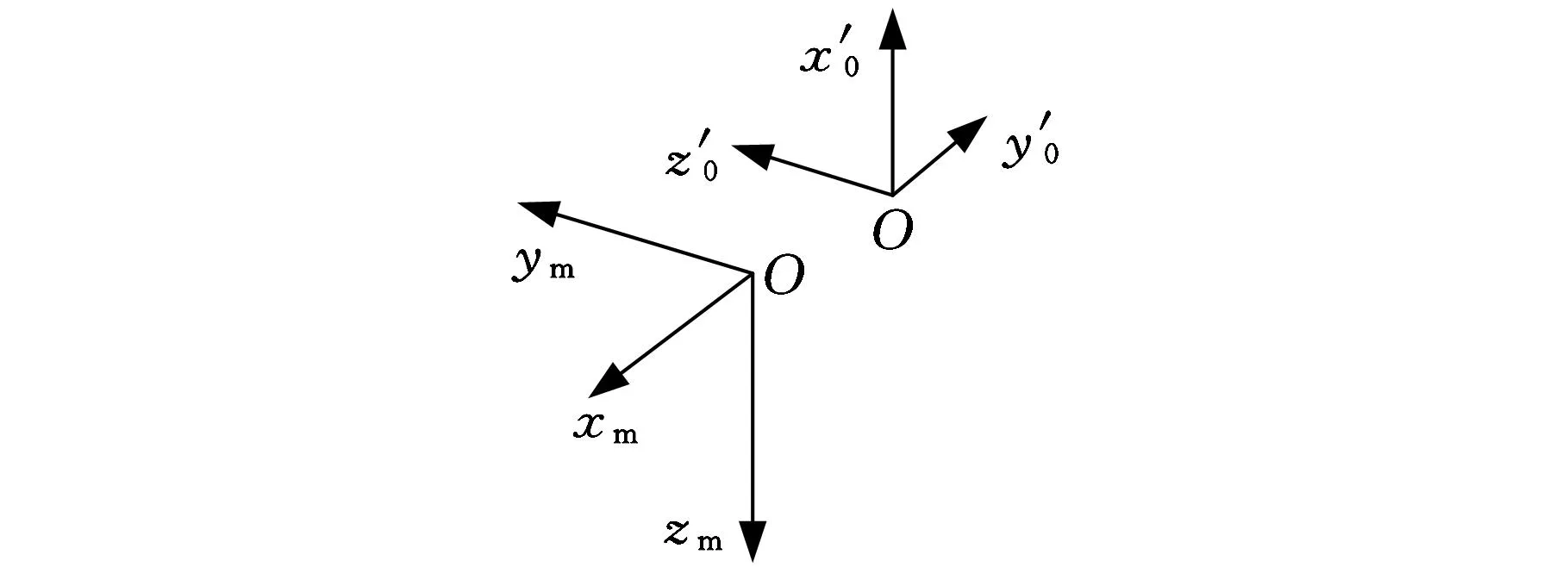
圖7　人體坐標系與過渡坐標系

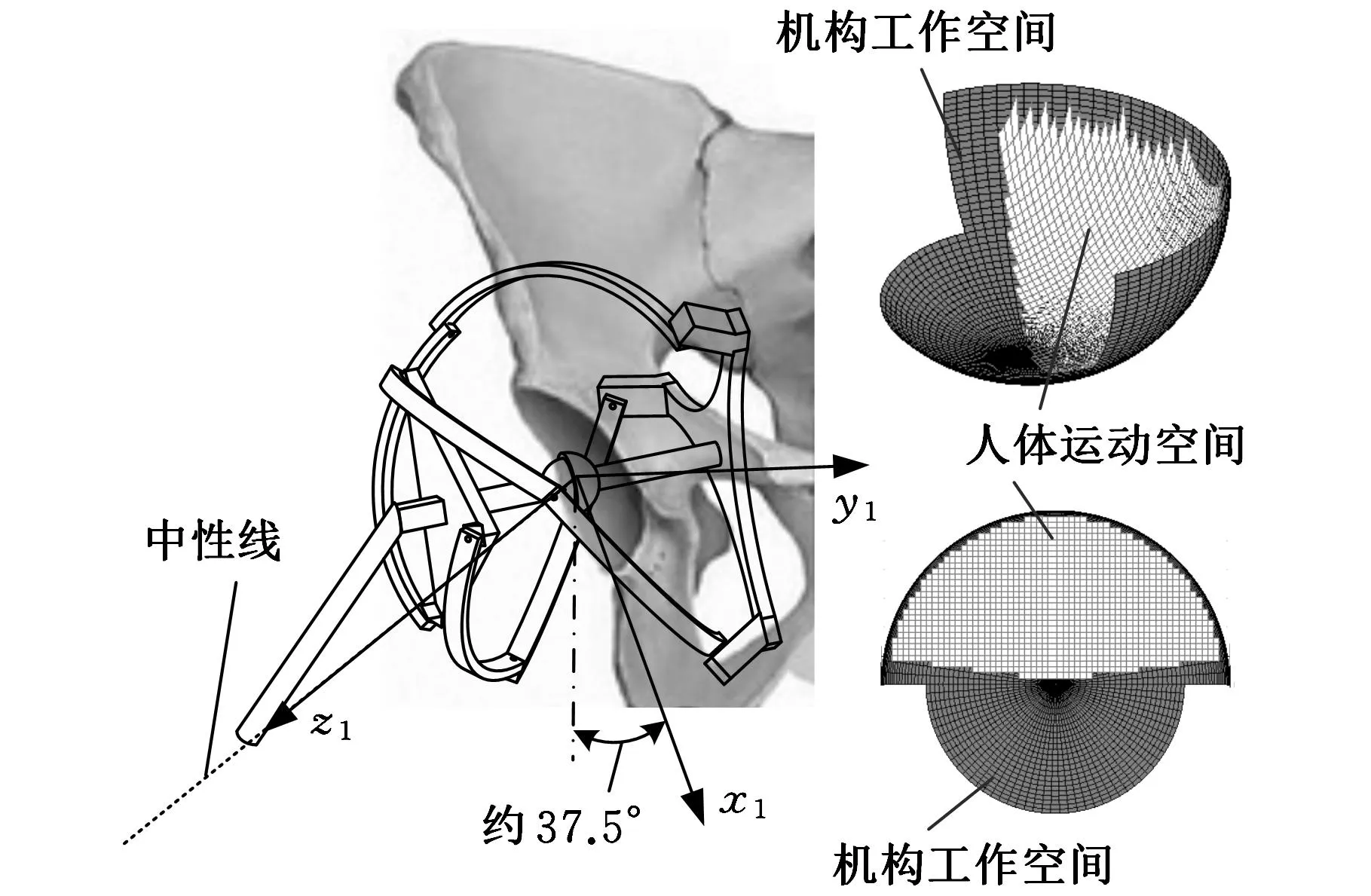
圖8　機構安裝定位依據

安裝到人體中的機構與人體坐標系如圖9所示，此時機構的固定坐標系改稱為機構在人體中的基準坐標系。根據人體的實際結構，保證機構工作空間與肢體運動范圍相協調，兼顧機構工作空間的對稱特性，經過反復計算和比對，取基準坐標系相對過渡坐標系安裝定位角α0=25°,β0=20°,γ0=45°。

圖9　關節安裝位置及人體坐標系

2.2仿生關節空間與機構空間映射關系

具有偏置輸出的三自由度球面并聯仿生關節的輸入端為3個驅動電機的轉角θ11、θ21、θ31；輸出端則為關節肢體在人體坐標系的三個擺角φxzt、φyzt、φzzt，由于關節采用偏置輸出、機構在人體中的定位姿態不同，因此兩端參數的關系比較復雜。必須建立仿生關節空間與機構工作空間的映射關系，即基于安裝定位角度α0、β0、γ0，建立3-RRR+(S-P)并聯機構動平臺位姿角φx、φy、φz與關節肢體的3個擺角φxzt、φyzt、φzzt的關系。再利用3-RRR+(S-P)并聯機構的運動學反解，最終求得3個驅動電機的輸入轉角與關節肢體的3個擺角的關系。

由圖7可知過渡坐標系{B}在人體坐標系{A}中的描述如下：

(2)

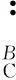
式中，s代表sin ，c代表cos ，下同。

基準坐標系{C}在人體坐標系{A}下的描述為

(3)

根據動坐標系在固定坐標系中的描述，求得偏置坐標系{P}在基準坐標系{C}中的描述為

(4)

r11C=cφycφz

r21C=cφysφz

r31C=-sφy

r12C=(sφxsφycφz-cφxsφz)ct+

(cφxsφycφz+sφxsφz)st

r22C=(sφxsφysφz+cφxcφz)ct+

(cφxsφysφz-sφxcφz)st

r32C=sφxcφyct+cφxcφyst

r13C=-(sφxsφycφz-cφxsφz)st+

(cφxsφycφz+sφxsφz)ct

r23C=-(sφxsφysφz+cφxcφz)st+

(cφxsφysφz-sφxcφz)ct

r33C=-sφxcφyst+cφxcφyct

另一方面，肢體運動位姿為φxzt、φyzt、φzzt時，關節肢體上的坐標系{I}在人體坐標系{A}中的描述為

r11I=cφyztcφzzt

r21I=cφyztsφzzt

r31I=-sφyzt

r12I=sφxztsφyztcφzzt-sφxztsφzzt

r22I=sφxztsφyztsφzzt+cφxztcφzzt

r32I=sφxztcφyzt

r13I=cφxztsφyztcφzzt+sφxztsφzzt

r23I=cφxztsφyztsφzzt-sφxztcφzzt

r33I=cφxztcφyzt

肢體在基準坐標系中描述如下：

整理得

(5)

r11D=r11I(sα0sβ0cγ0+cβ0sγ0)+r21I(sα0cβ0cγ0-sβ0sγ0)-r31Icα0cγ0

r21D=r11I(sα0sβ0sγ0-cβ0cγ0)+r21I(sβ0cγ0+sα0cβ0sγ0)-r31Isγ0cα0)

r31D=r11Isβ0cα0+r21Icβ0cα0+r31Isα0

r12D=r12I(sα0sβ0cγ0+cβ0sγ0)+r22I(sα0cβ0cγ0-sβ0sγ0)-r32Icα0cγ0

r22D=r12I(sα0sβ0sγ0-cβ0cγ0)+r22I(sβ0cγ0+sα0cβ0sγ0)-r32Isγ0cα0

r32D=r12Isβ0cα0+r22Icβ0cα0+r32Isα0

r13D=r13I(sα0sβ0cγ0+cβ0sγ0)+r23I(sα0cβ0cγ0-sβ0sγ0)-r33Icα0cβ0

r23D=r13I(sα0sβ0sγ0-cβ0cγ0)+r23I(sβ0cγ0+sα0cβ0sγ0)-r33Isγ0cα0

r33D=r13Isβ0cα0+r23Icβ0cα0+r33Isα0

式(4)、式(5)為同一構件經由不同的途徑在同一坐標系下的描述，矩陣中的所有元素對應相等，即

cφysφz=r11I(sα0sβ0sγ0-cβ0cγ0)+r21I(sβ0cγ0-sα0cβ0sγ0)-r31Icα0sγ0

cφycφz=r11I(sα0sβ0cγ0+cβ0sγ0)+r21I(sα0cβ0cγ0-sβ0sγ0)-r31Icα0cγ0

-sφy=r11Isβ0cα0+r21Icβ0cα0+r31Isα0

sφxcφyct+cφycφxst=r12Isβ0cα0+r22Icβ0cα0+r32Isα0

-sφxcφyst+cφxcφyct=r13Isβ0cα0+r23Icβ0cα0+r33Isα0

解方程組求得機構的姿態角函數

(6)

AI=r11I(sα0sβ0sγ0-cβ0cγ0)+

r21I(cβ0cγ0-sα0cβ0sγ0)-r31Icα0sγ0

BI=r11Isβ0cα0+r21Icβ0cα0+r31Isα0

CI=r12Isβ0cα0+r22Icβ0cα0+r32Isα0

DI=r11I(sα0sβ0cγ0+cβ0sγ0)+

r21I(sα0cβ0cγ0-sβ0sγ0)-r31Icα0cγ0

FI=r13Isβ0cα0+r23Icβ0cα0+r33Isα0

依據仿生學原理，經上述過程，定義本仿生髖關節在人形機器人中的安裝定位角度為α0、β0、γ0，依據該定位角度和偏置輸出角t，綜合給出了肢體運動空間與3-RRR+(S-P)機構空間映射關系(φxzt、φyzt、φzzt與φx、φy、φz之間的關系，即式(2)～式(5))，再結合仿生髖關節運動學正反解，就可完成本髖關節的設計和控制系統輸入輸出的關系。

3仿生髖關節運動學正反解

3.1運動學反解

3-RRR球面并聯機構的反解為已知球面三自由度機構上平臺相對于下平臺的姿態，求輸入轉角。根據中間轉動副ωi和動平臺轉動副νi之間的約束關系ωi·νi=cosα2(i=1,2,3)可求得機構的運動學反解：

(7)

i=1,2,3

將相關參數代入式(7)整理得髖關節運動學反解：

(8)

其中，參數θ11h、θ21h、θ31h為髖關節驅動器輸入角，根據裝配條件表達式中的“±”應取“-”，Ai、Bi、Ci是已知參數和機構參數的函數表達式。

3.2運動學正解

3-RRR球面并聯機構的正解為已知球面三自由度機構輸入轉角，求上平臺相對于下平臺的姿態矩陣，利用兩點間距離在不同坐標系中的表達不變，求解運動學正解[8]。

中間轉動副軸線方向矢量可表示為在定系中的表達和在動系中的表達。

在定系中的表達式為

(9)

在動系中的表達式為

(10)

其中，φi為中間轉動副的轉角,i=1,2,3。

所以有

(11)

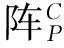
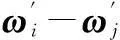
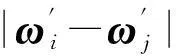
d1cφ1+d2cφ2+d3sφ1+d4sφ2+d5cφ1cφ2+

d6cφ1sφ2+d7sφ1cφ2+d8sφ1sφ2+d9=0

(12)

h1cφ2+h2cφ3+h3sφ2+h4sφ3+h5cφ2cφ3+

h6cφ2sφ3+h7sφ2cφ3+h8sφ2sφ3+h9=0

(13)

l1cφ3+l2cφ1+l3sφ3+l4sφ1+l5cφ3cφ1+

l6cφ3sφ1+l7sφ3cφ1+l8sφ3sφ1+l9=0

(14)

式中，dk、hk、lk(k=1,2,…,9)為已知參數和機構參數的函數表達式。

引入半角公式：

將半角公式代入式(13)，并經過消元最終整理得

(15)

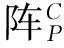
4數值驗證與模擬實驗

4.1數值驗證

原型機構基本參數：α1=90°，α2=90°，β1=60°，β2=45°，上下平臺鉸鏈點分別位于等邊三角形頂點上，即η11=η21=0，η12=η22=2π/3，η13=η23=4π/3。結合上文求得的安裝定位角度，同時取偏置角度t=50°，使用空間間的映射關系，對髖關節在不同運動姿態時，基準坐標系的偏轉角進行求解。

如圖4所示，3-RRR+(S-P)球面并聯機構的安全工作空間為：φx0、φy0在(-63°,63°)內，φz0在(-90°,90°)內，由表2中的計算結果可清晰看出，各個運動姿態所需在基準坐標系的旋轉角度，均在機構的安全工作空間內，故該仿生關節可實現人體髖關節的各個運動姿態。

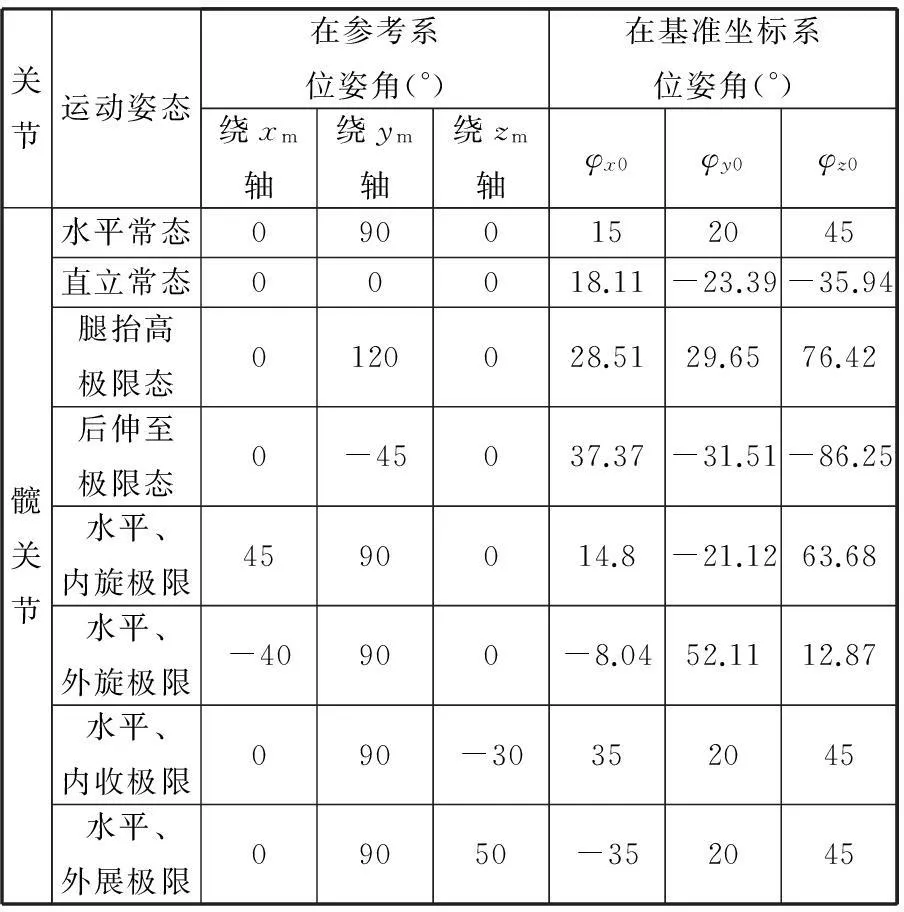
表2　關節運動特定狀態及機構位姿角

4.2模擬實驗

基于上述模型分析，為進一步驗證安裝角度和偏置角度的合理性，建立映射關系和正反解的正確性，及該仿生關節復現人體運動的能力，設計并進行了模擬實驗。具體模擬實驗的過程如下：如圖10所示，使用可穿戴式完全無線3D身體慣性跟蹤儀及磁性運動跟蹤器，采集人體髖關節在外伸、內收、前擺和后擺這些髖關節實際運動狀態下的位姿信息。依照前文獲得的數學映射關系、偏置角度t和安裝定位角度，將傳感器采集到的信息數據(圖11)在MATLAB下進行整合處理，實現信息由人體關節空間到該機構空間的變換，再利用求解的正反解關系，可獲得模型驅動的角速度隨時間變化的關系，圖12是其中一個驅動關節的角度、角速度隨時間變化的關系。

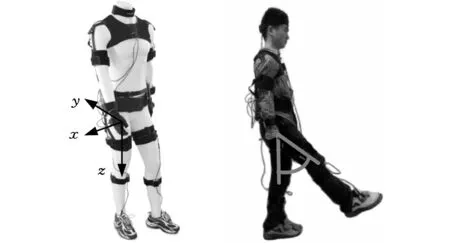
圖10　儀器坐標及穿戴方式

圖11　采集的大腿繞x軸轉角變化

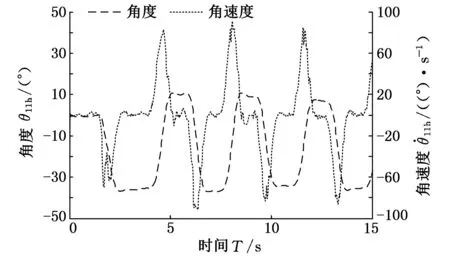
圖12　經轉換后獲取的驅動輸入

將運算得到的關節驅動信息，作為已建立模型的驅動輸入，導入到ADAMS模型中，進而校驗模型偏置端的運動姿態與實際人體關節姿態的關聯性。由于篇幅限制，本文只將髖關節屈伸運動(前后擺腿運動)的模擬結果予以展示，圖13為ADAMS中測繪到的仿生髖關節偏置端繞x軸轉角變化曲線。

圖13　ADAMS中仿生髖關節偏置端繞x軸轉角變化

從實驗結果易于看出，在人體大腿往復進行4次前后擺動的過程中(圖13)，人體大腿部分繞x軸的轉動角度變化約在-15°～58°，忽略步伐間的誤差，4次中彼此運動變化規律相仿，該運動近似呈周期性，符合人體實際運動規律。ADAMS仿真模型的偏置端角度(偏置端軸線與豎直垂線夾角)變化為-14.76°～56.38°，結合圖11、圖12和圖14，儀器測得的偏置端繞人體x軸的角度隨時間的變化關系與仿真結果相仿，誤差在10-5(°)(圖15)，該仿生髖關節基本上復現人體前后擺腿過程。

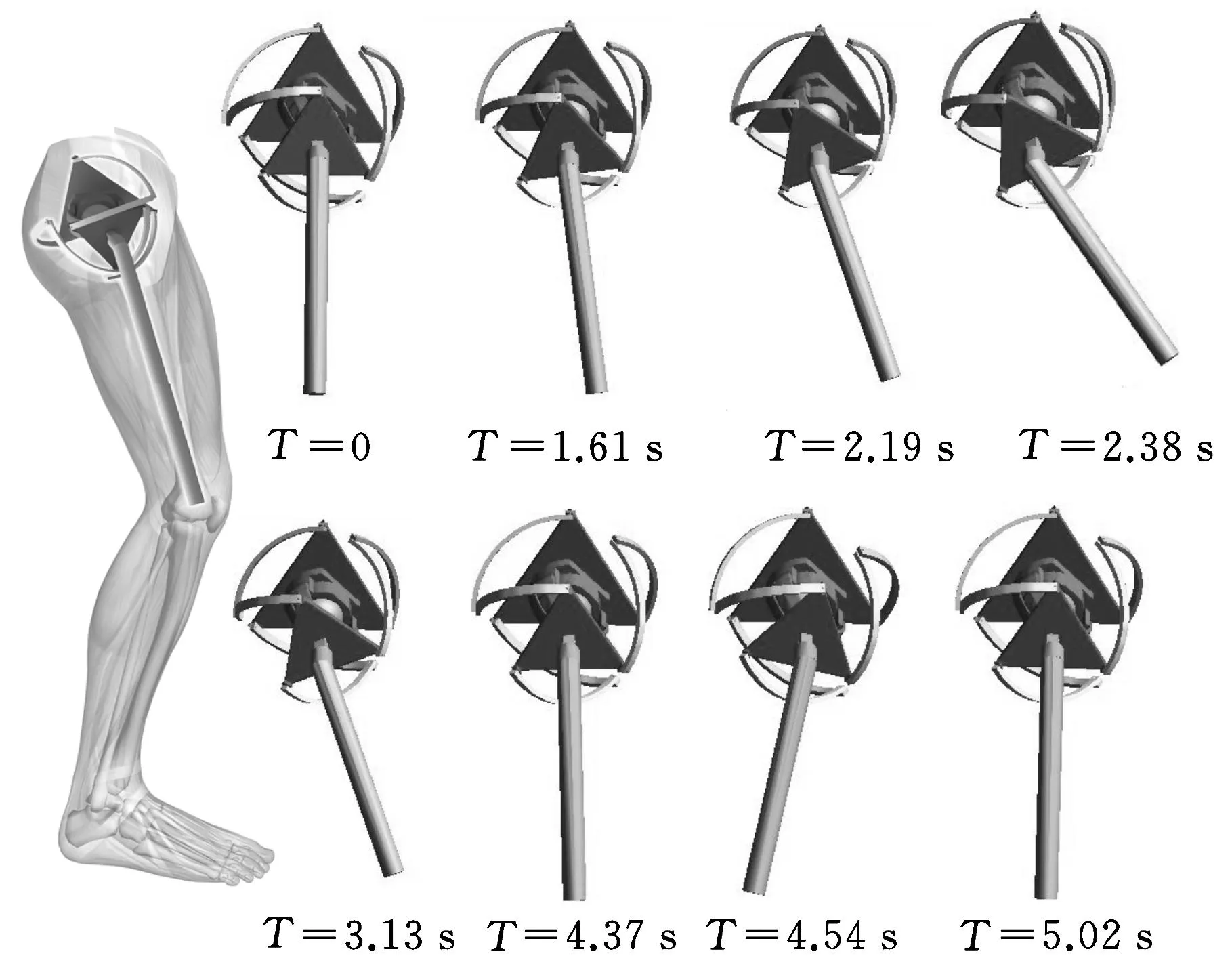
圖14　ADAMS模型動作效果

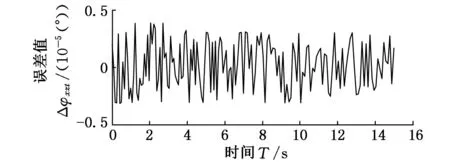
圖15　ADAMS模型仿真結果與儀器測量值的誤差

忽略具體人體與所建模型存在的差異性，該仿生髖關節的運動輸出和實際人體關節運動相仿，故本文所建立偏置輸出3-RRR+(S-P)球面并聯仿生髖關節的機構空間和人體關節空間映射關系和正反解運算是可以應用到實際仿生關節控制和信息處理的算法中的，同時也說明了本文建立的偏置角度和安裝定位角度的合理性。

5結論

(1)仿生關節空間可覆蓋髖關節的運動空間。提出基于3-RRR+(S-P)機構的關節機構工作空間與人體髖關節運動空間相協調的設計原則，進而確定關節機構的安裝定位角度，完成人形機器人髖關節的設計。

(2)從仿生學角度建立了該機構的工作空間與人體關節的運動空間的映射關系，并給出了仿生髖關節運動學正反解的解析表達式。

(3)設計并進行數值驗證和模擬實驗，該仿生關節可實現髖關節的8個基本運動姿態并對髖關節屈伸運動進行模擬復現，進一步證實了上述理論計算的正確性，展示了研究該仿生關節的實際價值，可為后序進行仿生髖關節樣機的研制、關節在人形機器人身上嫁接及安裝定位提供理論基礎和設計依據。

參考文獻：

[1]侯雨雷, 胡鑫喆, 周玉林. 新型過約束球面并聯式關節機構仿生設計[J]. 中國機械工程, 2014, 25(6): 723-726.

HouYulei,HuXinzhe,ZhouYulin.BionicJointDesignBasedonaNovelOver-constrainedSphericalParallelMechanism[J].ChinaMechanicalEngineering, 2014, 25(6): 723-726.

[2]GosselinCM,St-PierreE.DevelopmentandExperimentationofaFast3-DOFCamera-orientingDevice[J].TheInternationalJournalofRoboticsResearch, 1997, 16(5): 619-630.

[3]GoseelinCM,St-PierreE,MartinG.DevelopmentoftheAgileEye[J].Robotics&AutomationMagazine, 1996, 3(4): 29.

[4]TaoZJ,AnQ.InterferenceAnalysisandWorkspaceOptimizationof3-RRRSphericalParallelMechanism[J].MechanismandMachineTheory, 2013, 69: 62-72.

[5]楊加倫, 高峰, 戚開誠. 等.正交三自山度球而并聯機構的位置正反解新方法[J].機械設計與研究, 2009, 24(3): 30-32.

YangJialun,GaoFeng,QiKaicheng,etal.LocationOrthogonalThreeGoalsfromSantosandParallelMechanismForwardandInverseNewApproach[J].MechanicalDesignandResearch, 2009, 24(3): 30-32.

[6]SaafiH,LaribiMA,ZeghloulS.ForwardKinematicModelImprovementofaSphericalParallelManipulatorUsinganExtraSensor[J].Mechanism&MachineTheory, 2015, 91:102-119.

[7]黃田, 曾憲著, 曾子亞, 等.等頂錐角3自由度球面并聯機構的全參數解析尺度綜合[J].機械工程學報, 2000, 36(8): 15-19.

HuangTian,ZengXianzhu,ZengZiya,etal.SotheWholeArgumentParsingWhiteScalesTipAngle3DegreesofSphericalParallelSynthesis[J].JournalofMechanicalEngineering, 2000, 36(8): 15-19.

[8]高征, 高峰.球面3自由度并聯機構的正解分析新方法[J]. 機械設計與制造, 2006(9):122-124.

GaoZheng,GaoFeng.TheForwardNewApproachof3DOFSphericalParallelMechanism[J].MechanicalDesignandManufacture, 2006(9):122-124.

[9]張立杰, 劉辛軍. 球面三自由度并聯機器人可達工作空間的研究[J].中國機械工程，2001,12(10):1122-1124.

ZhangLijie,LiuXinjun.TheReachableWorkspaceofa3DOFSphericalParallel[J].ChinaMechanicalEngineering, 2001,12(10):1122-1124.

[10]賴一楠, 張廣玉, 段志鳴, 等.面向控制的3-RRR球面并聯機構正運動學實時解法[J]. 中國機械工程, 2003,14(2):113-115.

LaiYinan,ZhangGuangyu,DuanZhiming,etal. 3-RRRSphericalParallelMechanismforReal-timeControloftheForwardKinematicsSolution[J].ChineseMechanicalEngineering, 2003,14(2):113-115.[11]BaiS,HansenMR,AngelesJ.ARobustForward-displacementAnalysisofSphericalParallelRobots[J].Mechanism&MachineTheory, 2003, 37(2):185-204.[12]EnferadiJ,TootooncbiAA.ANovelSphericalParallelManipulatorForwardPositionProblem,SingularityAnalysisandIsotropyDesign[J].Robotica, 2009,27(5): 663-676.

[13]OkadaM,ShinoharaT,GotohT,etal.DoubleSphericalJointandBacklashClutchforLowerLimbsofHumanoids[C]//IEEEInternationalConferenceonRobotics&Automation.Taipei,2003:491-496.

[14]ChengGang,YuanXin,YuJingli,etal.KinematicCalibrationAnalysisof3SPS+1PSBionicParallelTestPlatformforHipJointSimulator[J].Measurement, 2013, 46(10):4152-4160.

[15]程剛, 于敬利, 袁欣,等. 3SPS+1PS髖關節并聯仿生試驗系統工作空間優化[J].機械工程學報, 2013, 49(23): 88-94.

ChengGang,YuJingli,YuanXin,etal.StudyonWorkspaceOptimizationof3SPS+1PSParallelHipJointSimulator[J].JournalofMechanicalEngineering, 2013, 49(23): 88-94.

[16]周玉林，高峰. 具有偏置輸出的3自由度球面并聯人形機器人仿生髖關節:中國,CN101301756[P]. 2008-11-12.

[17]邱雪松，楊龍，周玉林,等.新型大工作空間仿生被動球面鉸鏈構型及工作空間分析[J]. 中國機械工程, 2015,26(3):354-359.

QiuXuesong,YangLong,ZhouYulin,etal.ConfigurationandWorkspaceAnalysisofNovelBionicPassiveSphericalHingewithLargeWorkspace[J].ChineseMechanicalEngineering, 2015,26(3):354-359.

[18]FrankelVH,NordinM. 股骨系統基本生物理力學[M]. 黃慶森，單文文,譯. 天津: 天津科學技術出版社,1986.

(編輯王艷麗)

Bionic Hip Joints Based on Bias Output 3-RRR+(S-P) Spherical Parallel Mechanisms

Yang YajingSun TongshuaiZhou Yulin

Yanshan University,Qinhuangdao,Hebei,066004

Abstract：Based on the 3-RRR+(S-P) spherical parallel hip joints with bias output, according to the bionic principles and referring to the structure of the femur, this paper determined the offset angle of the joint mechanisms, presented the coordination of the working spaces of the hip joints and the mechanisms, and ascertained the installing and locating angle of the joints on human body, which completed the design of the new humanoid robot hip joints. The paper made the mapping relationship between the spaces of the bionic joints and the mechanisms and solved the inverse/forward kinematics of the bionic joints.The numerical calculation shows that the joint mechanism may realize the basic movements of human hips, as well as the wireless wearable 3D inertia tracking equipment and magnetic movement tracking equipment from Xsens Technology Co. for the human natural gait. After mapping transforms and inverse solving,the information was imported into ADAMS for test. The results, which also verify the practicability and scientific values of the joints, support the mapping installing characterized angle and inverse/forward solutions proposed.

Key words：bias output; bionics;hip sphericity; parallel mechanism

收稿日期：2015-07-21

基金項目：國家自然科學基金資助項目(51275443)

中圖分類號：TP24

DOI：10.3969/j.issn.1004-132X.2016.11.001

作者簡介：楊亞敬，女，1989年生。燕山大學機械工程學院碩士研究生。主要研究方向為人形機器人及仿生學。孫通帥，男，1991年生。燕山大學機械工程學院碩士研究生。周玉林(通信作者)，男，1961年生。燕山大學機械工程學院教授、博士研究生導師。