基于Y-D Law的偽裝工程管理問題博弈分析
文/陳都 穆祥靜 楊曉鶴 安瑞楠
?
基于Y-D Law的偽裝工程管理問題博弈分析
文/陳都穆祥靜楊曉鶴安瑞楠
摘 要:偽裝工程是一項復雜的系統工程,要想發現管理過程中存在的問題,必須采取成熟的理論,運用科學的分析問題方法。基于Y-D Law的偽裝工程管理博弈,是以Y-D法則(Y-D Law)為基礎,分析管理力度與偽裝效果之間的相互作用機理,并引入基于區間博弈的管理效果協調控制模型,對偽裝工程管理過程中的問題加以分析。
關鍵詞:Y-D 法則;偽裝工程管理;博弈分析
博弈論(Game Theory)發展至今,已對人們的生活和生產活動產生了較為深遠的影響。博弈理論的提出始于1944年出版的《博弈理論與行為》(The Theory of Games and Behavior)一書,它是John Von Neumann、Oscar Morgenstern等人合作研究的成果[1]。一直以來博弈論在管理學研究中都有著較高的應用價值,所以將博弈理論在偽裝工程管理研究中加以運用是十分科學的。
偽裝工程管理是我軍一項重要的軍事活動,參與單位包括軍隊院校、科研院所、施工單位以及使用維護單位等,是多組織、多屬性、多目標群體間的合作[2]。因此,從軍事利益角度考慮,偽裝工程的管理過程屬于一類較為復雜的博弈,參與合作的各個組織之間既存在著共同的軍事利益,又或多或少地存在一些矛盾與沖突,合作的達成與合作的運行方式均是合作方之間相互博弈的結果。
一、Y-D Law理論基礎
人們在認識事物的過程中總會受到各種影響因素的限制,導致對信息的獲取受到一定阻礙。管理力度與產品創造設計之間的關系,至今仍然是一個模糊的概念,很難做出清晰的判定,最為可信的觀點是由Robert M. Yerkes和John Dillingham Dodson等人于1908年利用Y-D法則(Y-D Law)提出的U形模型。通過心理學研究發現,被管理者的創造能力和情感壓力之間存在一個U形關系[3],如圖1所示。
根據上圖可以看出,被管理者的創造能力與精神壓力之間,并非存在著單調線性關系,而是更為接近于指數關系。與此同時,近年來國外科學家又通過大量試驗,證明了情感壓力主要受管理者管理力度影響,作用效果為被管理者的感知工作量(Workload),在與個體情感承受能力(Affect)、知識(Knowledge)和技能(Skills)等綜合影響因素相互作用下產生工作壓力,也就是情感壓力(Mental Stress)。在受多因素影響的情感壓力(Mental Stress)作用下,管理力度將以非線性動態設計與情感壓力-創造力關系控制模型[4](Nonlinear Design Dynamics and Mental Stress-Creativity Relation),如下式所述:

直接作用于被管理者的工作能力和創造能力,對于本文研究內容而言,即是工程偽裝效果[5]。工程偽裝效果的好壞將隨被管理者受到情感壓力的波動在小范圍空間內發生不規則變化。因此,對于偽裝效果與管理力度關系的量化,可將其變化數值以即定區間作為控制范圍開展研究。
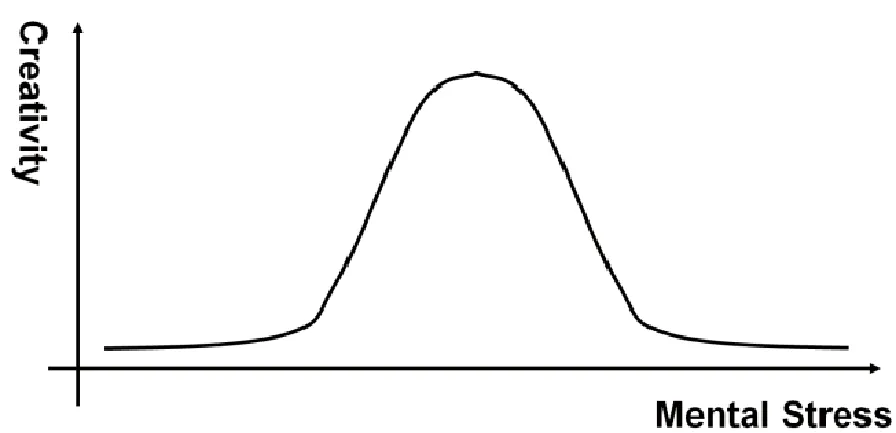
圖1 基于Y-D法則的創造能力與情感壓力關系模型
二、管理力度與偽裝效果之間的相互作用機理
對于一個偽裝工程而言,合理的管理力度會產生優良的偽裝效果,而不合理的管理力度則會影響偽裝效果。如果只是片面地強調某一方面,那么另一方面則很難得到保證。過于嚴格的管理將會使人員精神處于過度緊張狀態,工作出發點產生轉變,各部門之間的配合與協調能力喪失,這一變化將直接導致返工率的增加,拖延了工期,造成偽裝效果不可逆轉性的降低,甚至使工程暴露;如果是通過降低偽裝管理力度,提高各參建部門的積極性,以尋求更高的管理能力,在合理的控制范圍內會得到顯著效果,但是超出這一范圍則反而會對偽裝效果造成嚴重影響。因此,只有在一定范圍內尋求一個最為合理的偽裝管理力度,才是提高當前偽裝工程管理能力的關鍵。通過管理力度與情感壓力的作用關系和大量試驗數據統計,可以將Y-D Law模型轉化為管理力度與偽裝效果作用關系曲線[4][5][6],如圖2所示。
由上圖可以看出,當上層管理部門要求工程偽裝效果提升時,決策部門對基層單位的管理力度應隨之提高,但當管理力度達到某一峰值p時,其對偽裝效果的影響反而會有所下降,并在接近p2點時保持平穩不變;當決策部門適當放寬管理力度時,基層參建單位會酌情考慮采取一定的創新方法,盡力爭取自身利益的最大化,偽裝效果也因此會有所提升,但當管理力度減小到p1點時,偽裝效果也同時會下降到某一臨界值e1,此時決策部門如果不采取任何措施來調節管理力度,那么偽裝效果將持續下降,直至工程暴露。綜上所述,偽裝管理力度過高或過低都不能達到最佳的偽裝效果,因此有必要對管理力度與偽裝效果的區間臨界值,開展更加深入的研究。
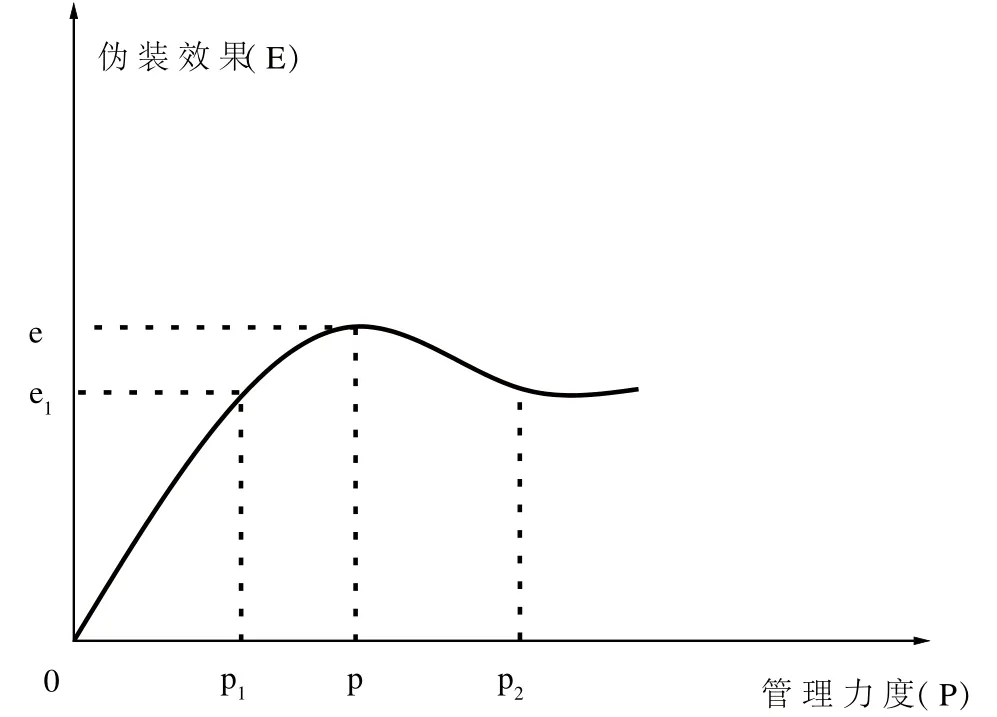
圖2 管理力度——偽裝效果關系圖
三、基于區間博弈的管理效果協調控制模型
(一)區間博弈模型的建立
要想用精確的數值對管理力度與偽裝效果之間的關系加以描述,難度較大,因此這里嘗試使用區間數的形式來建立博弈模型以彌補研究與現實之間的偏差,從而提高結論的可信度。設由管理力度和偽裝效果構成的博弈收益矩陣為B( )?,由此可將兩者之間的博弈問題稱為區間博弈問題,表示為,其中表示管理力度的備選策略集,E表示偽裝效果的備選策略集,而B( )?為博弈雙方預先使用區間數表達形式表示的收益矩陣。
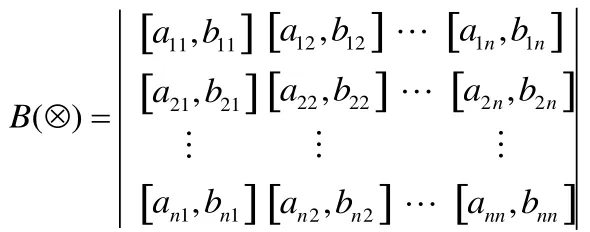
(二)最優策略解
管理力度與偽裝效果之間的博弈是在確保偽裝效果的前提下,通過對現有管理政策采取適當放寬或收緊的調節措施,求解博弈區間矩陣的最優策略值,從而獲得管理與效果間的最優協調控制方案。下文給出區間博弈最優策略解的求解方法。
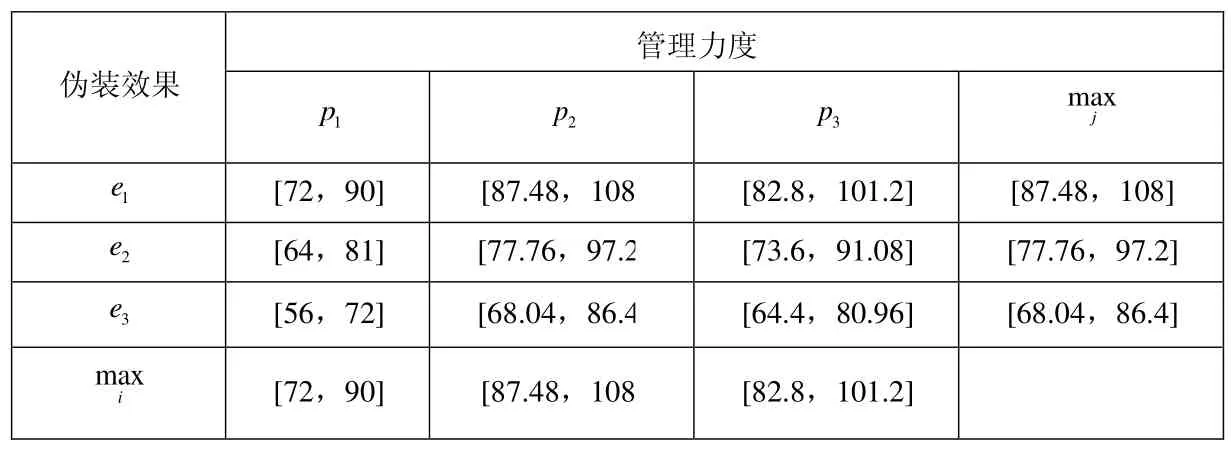
表1 偽裝效果與管理力度的區間博弈
為求解工程偽裝效果和管理力度博弈的最優策略解,首先要根據現有研究結論,完成以下假設:
①假設偽裝效果的策略集包含優、良、合格三個備選策略,并分別用(90,100]、(80,90]、(70,70]進行量化描述。
②引入工程偽裝效果保證率的概念。工程偽裝效果保證率,是指確保工程偽裝效果達到某一標準值的可靠程度。假設現行偽裝管理力度為1,當管理力度在0.8~0.9和1~1.1之間變化時,工程偽裝效果達到合格標準的保證率為100%;當管理力度在0.9~1之間變化時,偽裝效果達到優秀標準的保證率為100%。此時,用百分比表示管理力度,可得到管理力度的備選策略分別為(80%,90%]、(90%,100%]、(100%,110%]。
③通過經驗數據統計,并根據管理力度和偽裝效果之間的關系進行假設如下:當偽裝效果的合格保證率在100%時,管理力度每上升0.1,則優秀保證率下降5%~10%;當管理力度每下降0.1,則優秀保證率上升5%~10%[4][5]。
現通過區間博弈矩陣求解最優策略解,具體見表1所示。
根據最優策略解的求解方法可得到該博弈的最優收益值為[87.48,108],也就是說當管理力度在區間在[90%,100%]變化時,工程偽裝效果最佳,博弈雙方的收益最大。
四、結果分析
通過研究可以得到的啟示是,現階段我軍偽裝工程管理體系中,管理者一味增大偽裝管理力度,對工程偽裝效果并不一定能起到積極作用。從偽裝管理力度與偽裝效果之間的博弈關系中可以看出,當博弈雙方達到某一特定的臨界值后,偽裝效果反而會隨偽裝管理力度的增大遞減,也就是說,我軍現行的偽裝工程管理方法存在一定的問題。對于一些偽裝工程而言,雖然在開工前已經明確了工程的重要性,并同時加大了管理力度,但實際取得的效果并不好。究其原因,主要是由于各參建單位在過高的偽裝管理力度控制下,為了確保自身利益不受損失,而采取“各自為政,各搞一套”的措施響應,導致各單位之間的配合與協調能力嚴重缺失。而偽裝工程又是一項復雜的系統工程,系統中的每一個節點串聯形成系統運行的鏈條,這就要求節點之間具有良好的相互融合、相互包容作用效果。因此,在偽裝工程管理中,有必要引入一種更為先進的偽裝工程管理方法,以確保偽裝設計方案可用、偽裝技術研發實用、偽裝施工落實和偽裝維護統一。
(作者單位:解放軍后勤工程學院/海軍工程大學/解放軍96657部隊)
參考文獻:
[1] 羅云峰. 博弈論教程[M]. 北京:清華大學出版社,北京交通大學出版社,2007.
[2] 陳都,潘玉龍,安瑞楠. TOPSIS理論在國防工程偽裝決策中的應用研究[J]. 中國儲運,2015(1):164~166.
[3] Yerkes R M,Dodson J D. The Relation of Strength of Stimulus to Rapidity of Habitformation[J]. Journal of Comparative Neurology and Psychology,1908,18(5):459~482.
[4] Nguyen T A,Zeng Y. Effect of Stress and Effort on Self~rated Reports in Experimental Study of Design Activities[J]. Journal of Intelligent Manufacturing,2016: 1~14.
[5] Nguyen T A,Zeng Y. A Theoretical Model of Design Creativity: Nonlinear Design Dynamics and Mental Stress~Creativity Relation[J]. Journal of Integrated Design and Process Science,2012,16(3):65~88.
[6] Tang Y,Zeng Y. Quantifying Designer’s Mental Stress in the Conceptual Design Process Using Kinesics Study[J]. Proceedings of the 17th International Conference on Engineering Design. 2009.

