走出數據分析的“霧”區

□朱元生

?

走出數據分析的“霧”區

□朱元生

用樣本估計總體是統計的基本思想，通過對樣本數據的分析來了解總體是統計的基本方法.然而少數同學對統計量的意義理解不透，常會產生這樣那樣的誤區，現就幾類比較常見的問題舉例剖析如下，望能引起同學們的足夠重視.

一、對加權平均數的“權”理解不夠

例1東風超市備有某種綠色蔬菜100千克，上午按每千克1.2元的價格售出50千克，中午按每千克1元的價格售出30千克，下午按每千克0.8元的價格將剩下的蔬菜全部售完，試求這批蔬菜售出的平均價格是多少？

剖析：在3個不同時間售出的蔬菜中，由于售出蔬菜的重量不同，各個時間售出蔬菜的單價對平均價格的影響不同，因此這批蔬菜售出的平均價格不能簡單地用3個時間售出蔬菜價格的算術平均數來表示，而應該用加權平均數來計算.

=1.06（元/千克）.

答：這批蔬菜售出的平均價格為1.06元/千克.

二、對中位數的“中”理解不夠

例2在一次中學生田徑運動會上，參加男子跳高的15名運動員成績如下表所示：

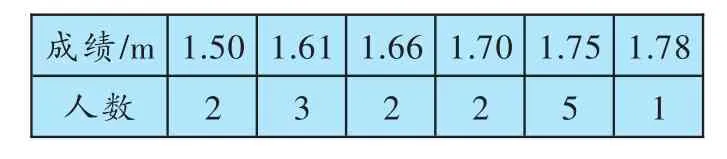
成績/m __人___ __數1.50 _ 2__ __ 1.61 _ 3__ __ 1.66 _ 2__ __ 1.70 _ 2__ __ 1.75 _ 5__ __ 1.78 1_

則這些運動員成績的中位數是多少？

剖析：從表中可以看出，跳高成績有6個數值，錯解就以最中間兩個數值的平均數作為這些跳高運動員成績的中位數，這是不正確的，共有15名運動員，按成績排序，跳高成績排列第8（最中間）的運動員的成績才是這些運動員成績的中位數.

正解：跳高成績排列第8的運動員的成績為1.70m，所以這些運動員成績的中位數為1.70m.

點評：將這組數據按大小順序排列，處于最中間位置的一個數據（或最中間兩個數據的平均數）就是這組數據的中位數，可知中位數不一定是數據中的數.還應注意中位數的單位與原數據的單位一致.

三、對眾數的“眾”理解不夠

例3“只要人人都獻出一點愛，世界將變成美好的人間”.在今年的“慈善一日捐”活動中，某中學八年級（2）班50名學生自發組織獻愛心捐款活動.班長將捐款情況進行了統計，并繪制成了統計圖.試根據下圖提供的信息，確定捐款金額的眾數.

錯解：眾數為20.

剖析：錯解以為捐款30元的人數最多為20人，所以眾數就是20，把出現次數最多的數據的次數錯以為是眾數.這是對眾數的“眾”理解不夠.

正解：從圖中可以看出，捐款30元的人數最多，所以捐款金額的眾數是30元.

點評：在確定眾數時，易把出現次數最多的數據的次數錯認為是眾數.應注意眾數是出現次數最多的數據，而不是出現的次數.一組數據的眾數有時不止一個，當出現次數最多的數據是n個時，則這組數據的眾數就有n個.眾數的單位與原數據的單位一致.

四、對極差、方差的“差”理解不夠

例4甲、乙兩名射擊運動員參加某大型運動會的預選賽，在相同條件下他們分別射擊5次，甲命中的環數為：9，8，9，9，10；乙命中的環數為：7，10，9，10，9.如果甲、乙中只能有1人入選，你認為入選者應該是誰？為什么？

錯解：入選的應該是甲.

根據題意，得

甲、乙兩人的平均數相等，而甲的極差是2，乙的極差是3，所以入選的應該甲.

剖析：欲確定哪位選手，需判斷哪位選手的射擊成績平均數大且較穩定，極差是指一組數據中最大數據與最小數據的差，它只能反映這組數據的變化范圍，而方差才是用來衡量一組數據波動大小的統計量.

正解：入選的應該是甲.

根據題意，得

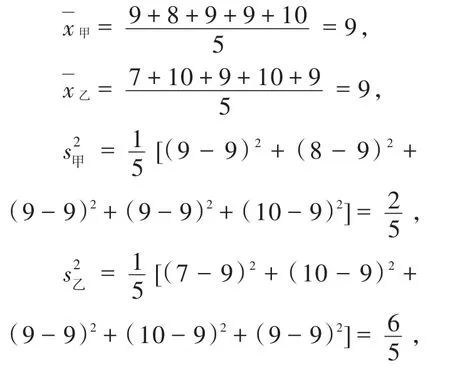
因為x甲=x乙，他們的平均數相同；而，甲的方差小于乙的方差，即甲的射擊成績比乙穩定些，所以入選的應該是甲.

點評：方差是刻畫一組數據波動大小（離散程度）的重要量度.一般而言，一組數據的方差越小，這組數據就越穩定；兩組數據中極差大的并不一定方差也大；極差、方差和標準差都有單位，其中極差和標準差的單位與已知數據的單位相同，使用時應當標明單位，方差的單位是已知數據單位的平方，使用時可以不標注單位.

五、對分類討論的“類”理解不夠

例5已知數據10、10、x、8的中位數與平均數相等，求這組數據的中位數.

錯解：當x=8時，這組數據的中位數是9，平均數也是9，所以這組數據的中位數為9.

正解：（1）當x≤8時，該組數據從小到大順序排列應為x、8、10、10，這時中位數為9，則，解得x=8，所以此時中位數為9；

（2）當8＜x≤10時，該組數據從小到大順序排列應為：8、x、10、10，這時中位數為，則，解得x=8，不在8＜x≤10內，此時x不存在；

（3）當x≥10時，該組數據從小到大順序排列應為：8、10、10、x，這時中位數為10，則，解得x=12，所以此時中位數為10.

綜上所述，這組數據的中位數為9或10.

點評：分類討論思想是初中數學中的重要思想方法，當問題可能出現多種情況時，要對可能出現的各種情況進行不遺漏、不重復的分類討論，才能得出完整的結論.