線結構光傳感器測頭參數優化與物鏡設計

殷 歡 合肥工業大學儀器科學與光電工程學院 安徽合肥 230009

?

線結構光傳感器測頭參數優化與物鏡設計

殷 歡 合肥工業大學儀器科學與光電工程學院 安徽合肥 230009

【文章摘要】

線結構光傳感器測頭是非接觸三維測量的關鍵部件，測量精度影響三維位置信息提取的準確性。本文基于激光三角法建立線結構光測頭的數學模型，基于透視投影建模完成成像坐標系與世界坐標系的轉換。研究系統綜合測量誤差與結構參數的關系，給出目標方程與邊界函數，用matlab軟件對結構參數仿真與優化。選取合適的結構參數后用zemax軟件設計滿足要求的物鏡結構。

【關鍵詞】

線結構光；數學模型；結構參數；matlab；zemax

0　引言

隨著工業對測量精度要求越來越高，利用光學技術進行非接觸測量是最具潛力的三維測量方法。其優點是系統柔性好、量程大、速度與精度適中。線結構光傳感器基于激光三角法，激光器將結構光投影到三維物體，再以一定角度漫反射回位置探測器，由探測器接收面位移算出物體表面點的三維坐標。系統結構決定測量范圍與精度，分析結構參數對結果的影響十分必要。

本文基于激光三角法建立測頭數學模型，透視投影建模轉換成像坐標系與世界坐標系，研究系統綜合測量誤差與結構參數的關系，給出目標方程與邊界函數，結合非線性規劃思想用matlab對結構參數仿真優化。選取合適的結構參數后用zemax設計滿足要求的物鏡結構。

1　線結構光傳感器測頭數學模型的建立

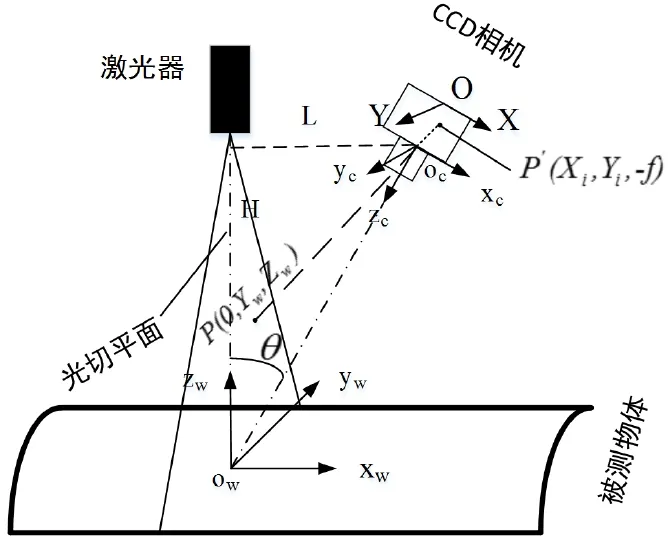
圖1　透視投影測量原理圖

構造測頭數學模型是本文的關鍵內容。三角法是從光源發射光線到被測表面，在另一向透鏡成像觀察入射點位置，入射與反射光線空間位置成三角形。按入射光與被測目標法線間角度關系分為直射式和斜射式。直射法建模具有代表性，本文選擇分析直射法，透視投影建立數學模型。透視投影變換在齊次坐標下進行，測量原理如圖1所示。

圖1中Ow-XwYwZw和Oc-XcYcZc為世界坐標系和攝像坐標系，是三維空間坐標系；O-XY為物體成像二維坐標系；X、Y軸平行于Xc、Yc軸。世界坐標系由攝像坐標系與光切平面唯一確定。Zc軸斜向下與光切平面交點為世界坐標系原點Ow；Zw軸在光切平面內垂直向上，在Zc軸和Xc軸決定的平面內；Yw軸在光切平面內與Yc軸平行；Xw軸垂直于光切平面。物體曲線方程為：

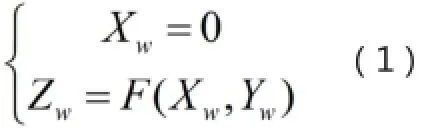
視場內線段經物鏡成像在像平面，物體表面在Zw軸偏離XwOwYw平面使光線成像與Y軸不重合，偏移量由Zw值決定。本文要建立世界坐標系點P（0，Yw，Zw）與攝像坐標系點P’（Xi，Yi，-f）的關系式，f為攝像物鏡焦距。把世界坐標點寫成齊次坐標形式（Xw，Yw，Zw，1），攝像坐標點為（Xc，Yc，Zc，1），世界坐標系經坐標平移使Ow與Oc重合，繞X軸旋轉180°，再繞Y軸旋轉-θ（右手坐標系從正半軸向原點看逆時針是正方向，這里按右手定則是反方向取負號）后轉換成攝像坐標系。表達式如下：

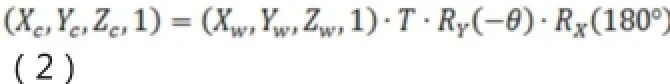
式中RY（-θ）和RX（180°）代表繞Y軸和X軸旋轉的矩陣，T代表平移矩陣，其表達如下：

將世界坐標系光切平面坐標點集（0，Yw，Zw，1）帶入公式（2），Yw、Zw為未知量，得攝像坐標點集：

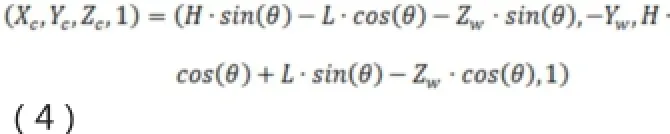
將圖像坐標系P’點轉換到攝像坐標系，齊次坐標形式表示（Xi，Yi，-f，1），聯立公式，結合，得世界坐標系光切平面點和攝影坐標系圖像傳感器點之間的關系式：

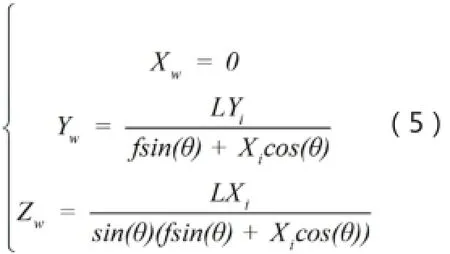
式中（Xw，Yw，Zw）為世界坐標系被測物體點的坐標，（Xi，Yi，-f）為圖像坐標，θ為物鏡光軸與光切平面夾角，L是物鏡中心到光切平面垂直距離，在透視坐標系下便于分析外部參數L、θ。

2　線結構光傳感器測頭結構參數分析與優化

本節利用數學模型分析結構參數，給出約束條件，根據主要影響因子進行優化設計，結合實例給出最優參數，盡量使測量誤差達到最小。

2.1結構參數設計分析

測量模型中世界坐標系Yw和Zw是L、θ、f、Xi和Yi的函數，根據誤差理論分析得Yw和Zw測量誤差與各自變量有關，可得：

其中ΔL、Δθ、Δf是結構參數L、θ、f的標定誤差，ΔXi和ΔYi為像面坐標Xi和Yi提取誤差。系統綜合測量誤差△為：

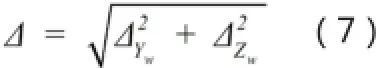
有兩種因素影響被測表面點坐標測量誤差：結構參數L、θ、f的標定誤差和圖像處理中像點坐標提取誤差。給定系統參數固定不變，使用前精確標定，因此ΔL、Δθ、Δf影響很小，主要誤差是像點坐標提取誤差。實際中像點坐標提取誤差隨算法改變，在此令ΔXi和ΔYi為一定值δ。利用式（5）Yw、Zw坐標分別對Xi、Yi求偏導，得被測面上點在Yw、Zw軸方向測量誤差，再由式（7）得系統綜合測量誤差：

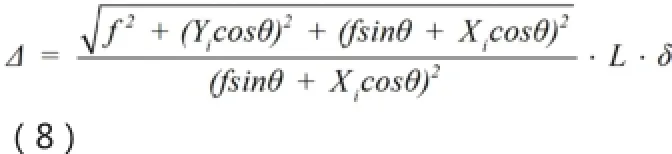
由上得△隨被測點位置不同而改變，在物面分布不均勻；△值隨f和θ增加單調減小，隨L和δ增加單調增加。設圖像傳感器尺寸2CX×2CY，Xi∈［-CX，CX］、Yi∈［-CY，CY］；得△在Xi=-CX，Yi=±CY時最大。要在視場內測量精度都達標，即△最大時要符合要求，得：

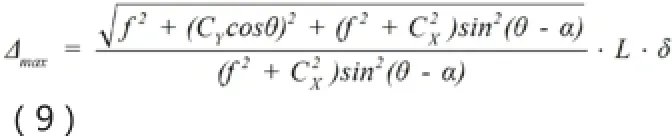
式中θ為線激光漫反射到物鏡的角度，實際要考慮光能量，把漫反射光條近似為郎伯輻射體，光條輻射強度滿足余弦定理，隨θ余弦變化，當θ為90°光強為0，即θ不能太大，否則不能捕捉清晰圖像。式中α為視場半角小于θ值，即，實際中圖像傳感器不能探測無窮遠處物點。當CX、CY已知，△max為L、f、θ的函數，把公式（9）定為結構目標函數，常取最小值時的結構參數量。當像面尺寸已知，由公式（5）可得Zw、Yw最小值和最大值。

2.2設計實例

本文設計一個輕型線結構光測頭，提出設計指標：綜合測量誤差小于0.020mm，測量深度范圍80-120mm，寬度范圍50-80mm，響應速度快，外形尺寸緊湊。

本文選取Thorlabs L650P007型號TO封裝半導體激光器，標準光輸出功率7mW，標準波長650nm，門限電流20mA，正常工作電流和電壓為28mA和2.2V，垂直方向半光束發散角28°，平行方向半光束發散角9°，最大象散值15μm，監測電流0.12mA。數字圖像傳感器選用Aptina IMAGING MT9P031型號1/2.5-Inch 5Mp CMOS傳感器，像面尺寸5.70×4.28mm，對角線長7.13mm，像元大小2.2×2.2μm，有效像素2592H×1944V，最高幀率53fps，支持數字和模擬信號輸出。常用工業鏡頭焦距有8mm、12mm、16mm、25mm，取像素提取誤差為1/4個像元尺寸，將已知參數帶入目標函數與約束方程，優化出合適的結構參數。基本約束：傳感器尺寸L為70-120mm，θ值大于α，由焦距與圖像傳感器尺寸確定。

此優化模型為非線性規劃問題，用matlab對結構參數仿真優化，由于選取初值不確定，可得多組滿足要求的結構參數，表1只列出不同焦距f的部分仿真數據：

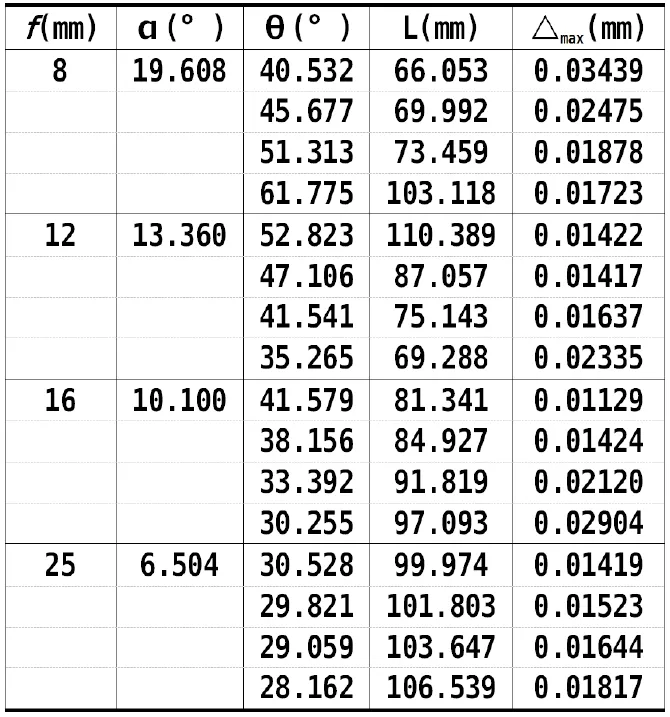
表1　不同f值下結構參數部分仿真結果

由圖2得綜合測量誤差與結構參數L、θ的關系，L與△max呈線性關系，△max隨L增大而增大；焦距與△max呈非線性關系，一定范圍內△max值隨f增加而降低。綜合考慮相機視場、測頭尺寸和設計要求，從仿真結果中選取合適的結構參數：f =12mm，θ=47°，L=87mm，△max=0.01417mm，滿足要求。

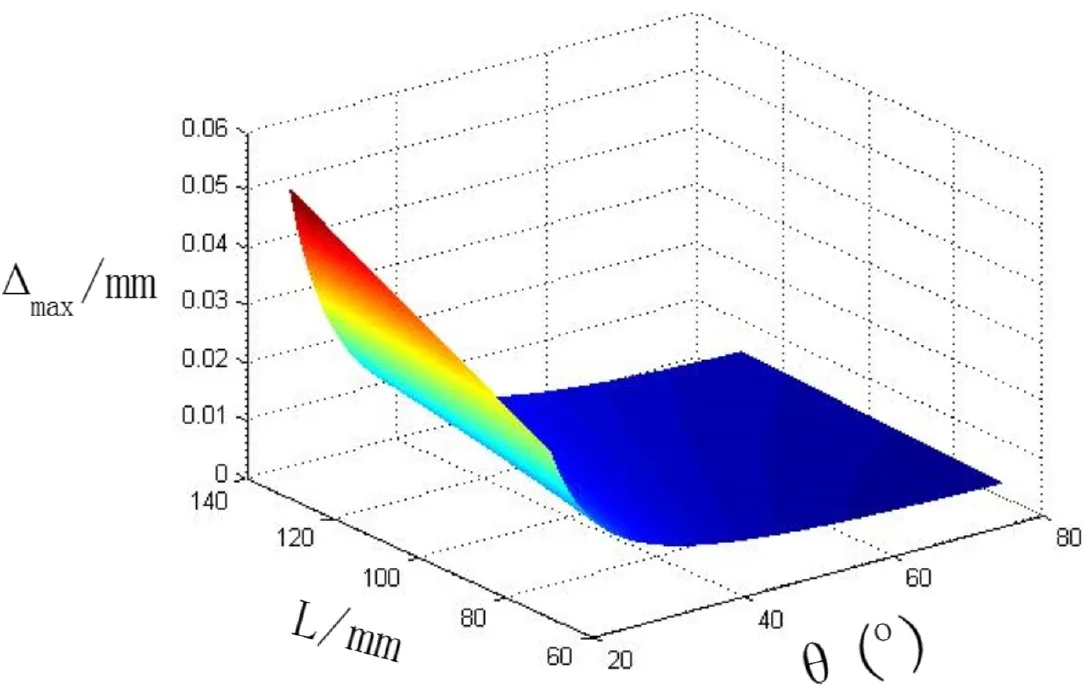
圖2　綜合測量誤差與L、θ關系圖

3　線結構光傳感器測頭物鏡設計

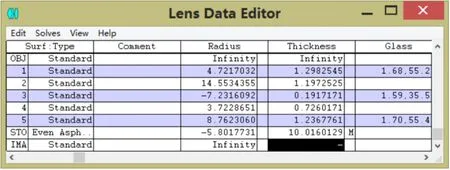
圖3　系統結構數據圖

攝影物鏡光學特性由焦距f、相對孔徑和視場角共同決定。焦距為12mm；相對孔徑由像面照度和物鏡分辨率決定，普通攝影物鏡為1：9～1：2.8，CMOS傳感器對角線ymax為7.13mm，得相對孔徑D/f’=1：3.37，實際設計取更大值；視場角由焦距和像面大小決定，半視場角ω=arctan（ymax/2f’）=16.54°，視場角2ω=33.08°。本文從光學設計手冊選取近似結構，通過縮放焦距法得到初始結構。

查詢后選定初始結構為后置光闌的三片物鏡，初始參數：焦距f’=42.12mm，相對孔徑1：2.8，視場角2ω=54°。初始結構效果一般，要添加MTFA、MTFT、MTFS操作數控制衍射調制函數在空間頻率內高于一定值，也要添加鏡片邊界函數控制各鏡片中心和邊緣厚度，還要添加像差操作數SPHA、COMA、ASTI、DIST等來控制系統基本像差，然后根據實際情況添加TTHI、OPGT等操作數來進行優化，得到最終結構如圖3-8：

系統第6面采用非球面，其余面是標準球面，在zemax中用合適的優化函數和操作數校正像差，逐步進行像差平衡，獲得實際焦距12.011mm的物鏡鏡頭，總畸變不超過0.4%，所選視場內MTF軸上超過70%@100lp/mm，軸外0.7071超過35%@100lp/mm，MTF曲線比較理想，整個系統球差0.000223，彗差-0.002911，像散-0.000304，鏡頭總長14.666mm，鏡頭結構緊湊，像質較好，滿足設計要求。

4　總結

在線結構光傳感器測頭數學模型基礎上分析各結構參數對綜合測量誤差的影響，綜合考慮測量精度和像素提取誤差，建立優化目標方程和邊界條件，結合非線性規劃思想用matlab軟件對結構參數仿真優化，得到理想的結構參數，再用zemax軟件設計滿足要求的物鏡結構，對線結構光傳感器測頭結構參數優化與物鏡設計有理論指導意義。

【參考文獻】

［1］王寶光，賀忠海，陳林才，等.結構光傳感器模型及特性分析［J］.光學學報，2002，22（4）：481-484.

［2］張廣軍，王紅，趙慧潔，等.結構光三維視覺系統研究［J］.航空學報，1999（4）：78—80.

［3］熊會元，陳承鶴，宗志堅.線結構光視覺傳感器設計優化［J］.工具技術，2009（9）：81—83.

［4］金文燕，趙輝，陶衛.激光三角測距傳感器建模及參數優化研究［J］.傳感技術學報，2006，19（4）：1090-1093.

［5］Zhang Jianxin，Djordjevich Alexandar.Study on laser stripe sensor［J］.Sensors and Actuators，1999，72（3）：224—228.

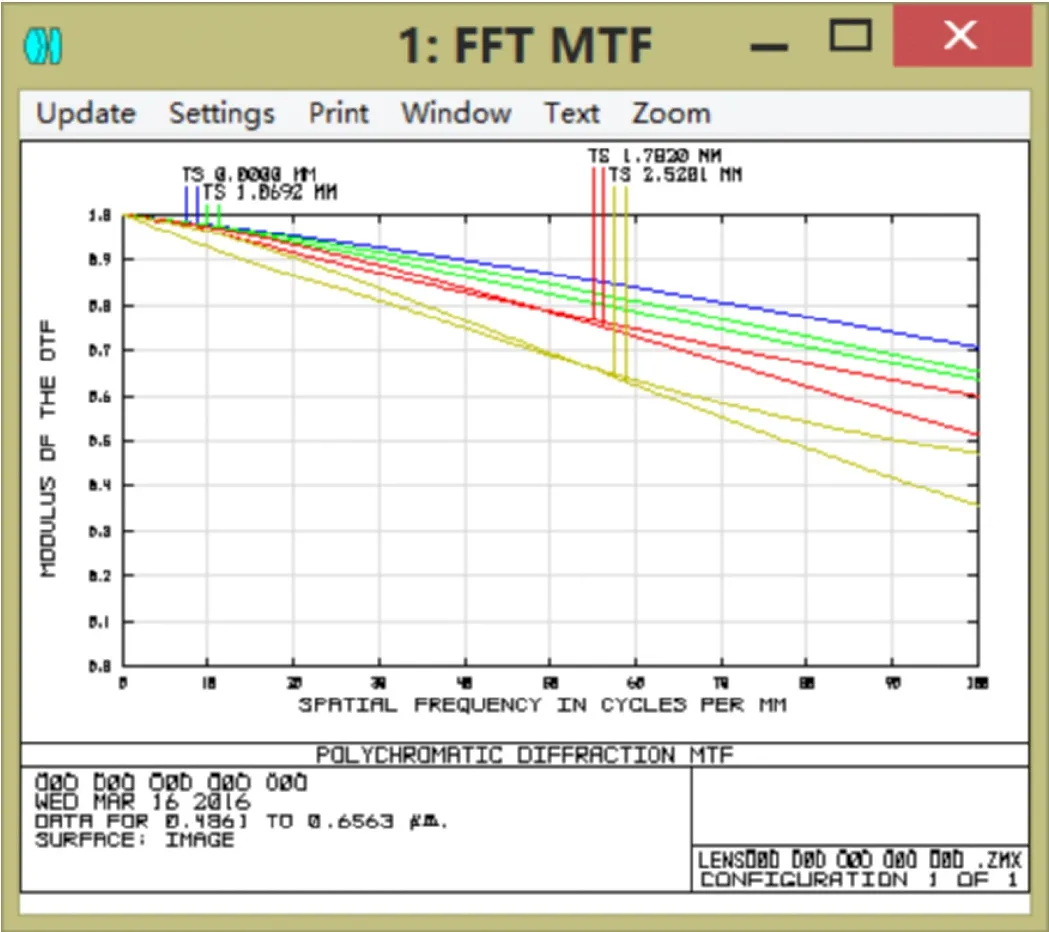
圖4　MTF曲線圖

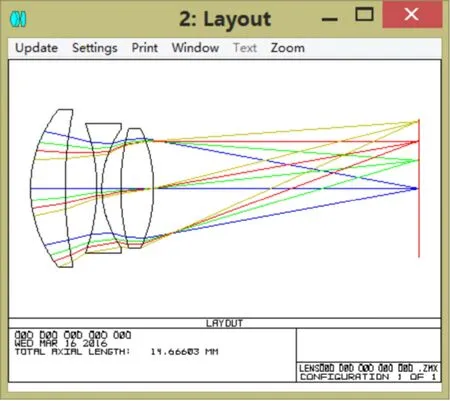
圖5　成像系統結構圖

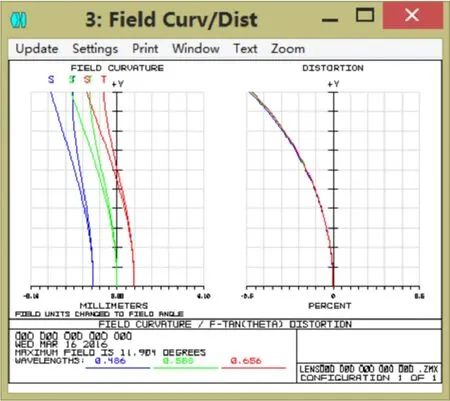
圖6　場曲和畸變圖

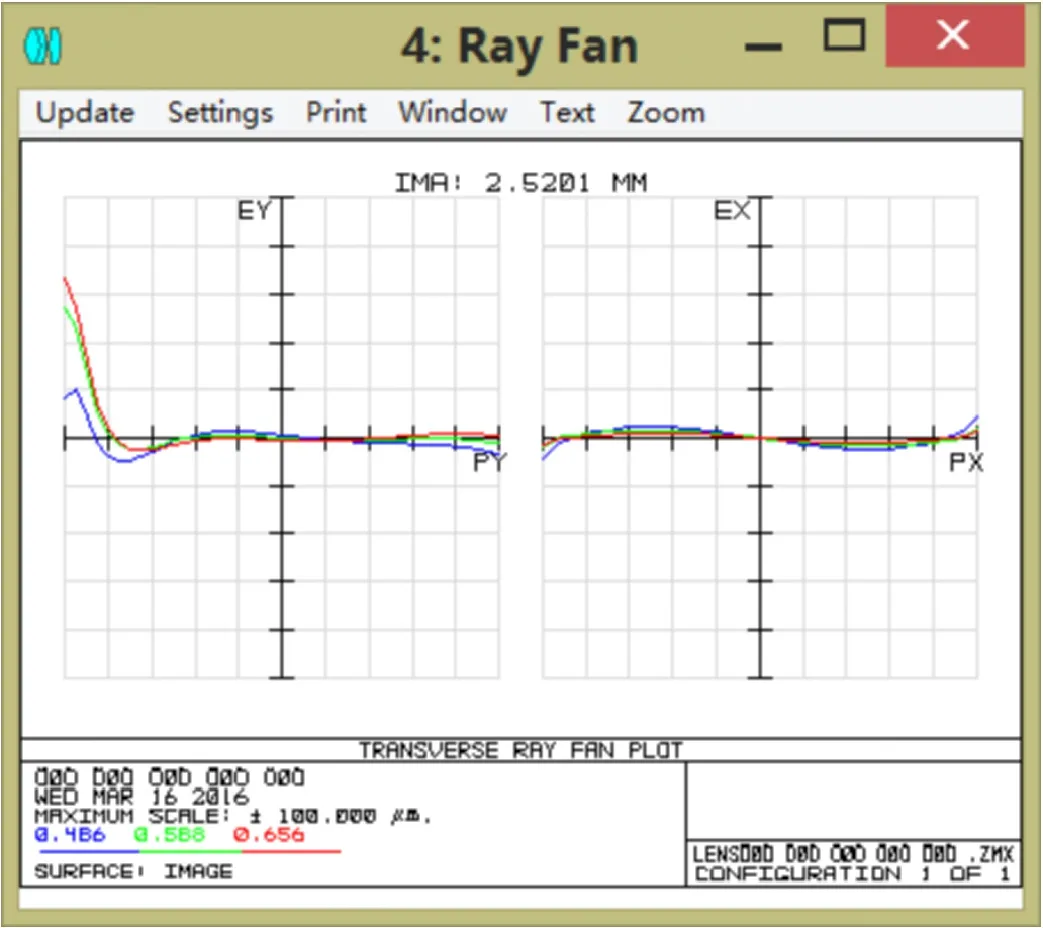
圖7　光線扇形圖

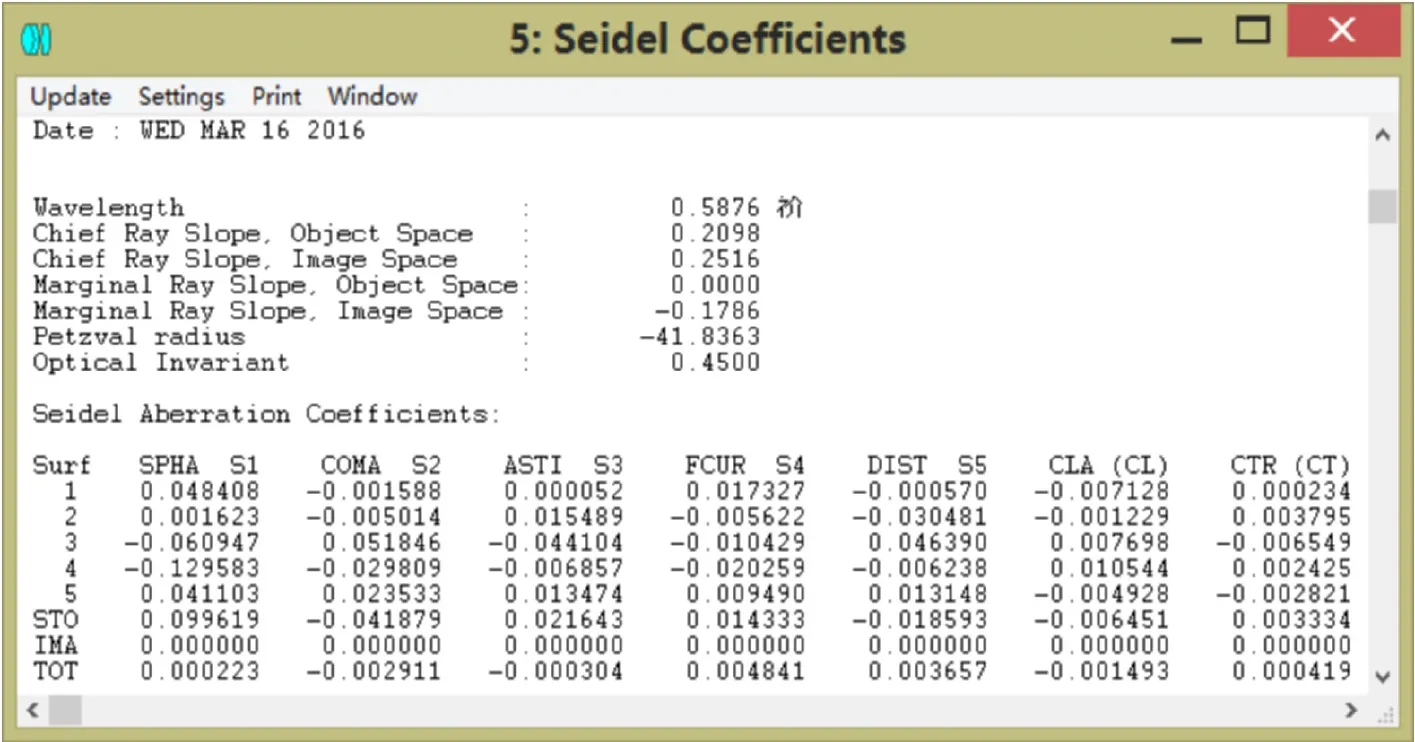
圖8　賽德爾系數圖