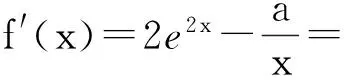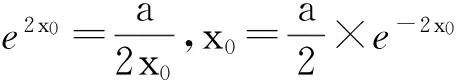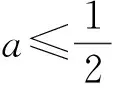利用導數(shù)求解函數(shù)的零點問題

◇　北京　丁益祥(特級教師)

利用導數(shù)求解函數(shù)的零點問題

◇北京丁益祥(特級教師)

函數(shù)的零點是函數(shù)的重要概念之一,這類問題的處理,除了涉及函數(shù)零點的存在定理以外,一般還與函數(shù)的單調性、方程和不等式等知識有關.而上述內容又和導數(shù)有著緊密的聯(lián)系,因此相關問題的求解,往往需要利用導數(shù)這一重要工具.

(1) 求a的值;

(2) 證明:當k<1時,曲線y=f與直線y=kx-2只有1個交點.

(2) 2曲線的交點問題,可以轉化成函數(shù)的零點問題來解決.

由(1)知函數(shù)f(x)=x3-3x2+x+2.設g(x)=f(x)-kx+2=x3-3x2+(1-k)x+4,則g′(x)=3x2-6x+1-k.因為k<1,故1-k>0.

又g(-1)=k-1<0, g(0)=4>0,故g(x)在區(qū)間(-1,0)上有零點.

又當x≤0時,g′(x)=3x2-6x+1-k>0,g(x)單調遞增，所以函數(shù)g(x)在區(qū)間(-∞,0]上有唯一零點.當x>0時,令h(x)=x3-3x2+4,則g(x)=h(x)+(1-k)x>h(x).h′(x)=3x2-6x=3x(x-2),由h′(x)>0,得x>2;由h′(x)<0,得0

故h(x)在(0,2)單調遞減,在(2,+∞)單調遞增,所以g(x)>h(x)≥h(2).

所以函數(shù)g(x)在(0,+∞)沒有零點.

綜上,函數(shù)g(x)在(-∞,+∞)上有唯一零點,即曲線y=f(x)與直線y=kx-2只有1個交點.

(1) 討論f(x)的導函數(shù)f′(x)的零點個數(shù);

(2) 證明:當a>0時f(x)≥2a+aln(2/a).

至此,我們已經(jīng)找到了區(qū)間的一個端點a,并且f′(a)>0.根據(jù)函數(shù)零點的存在定理,還需找到區(qū)間的另一個端點,并且希望在這個端點處f′(x)的值小于0，則在這個區(qū)間內f′(x)有零點.然而,這個端點不易找出，下面利用有限與無限思想來分析.

當x→0+時,f′(x)=2e2x-a/x→-∞.結合f′(a)>0,可以肯定在(0,a)內f′(x)必有零點.

設函數(shù)g(x)=2e2x與φ(x)=a/x,則這2個函數(shù)的圖象在第1象限內有且只有1個交點,所以f′(x)在(0,+∞)內有唯一零點.

(2) 由(1)可設f′(x)在(0,+∞)唯一零點為x0.注意到(1)中已證得f′(x)在(0,+∞)單調遞增,因此,當x∈(0,x0)時,f′(x)<0;當x∈(x0,+∞)時,f′(x)>0.故f(x)在(0,x0)單調遞減,在(x0,+∞)單調遞增,所以當x=x0時,f(x)取得最小值,最小值為f(x0).

2a+aln(2/a).

故當a>0時,f(x)≥2a+aln(2/a).

(1) 設g(x)是函數(shù)f(x)的導函數(shù),求函數(shù)g(x)在區(qū)間[0,1]上的最小值;

(2) 若f(1)=0,函數(shù)f(x)在區(qū)間(0,1)內有零點,證明:e-2

由f(x)=ex-ax2-bx-1,得g(x)=f′(x)=ex-2ax-b，g′(x)=ex-2a.容易看出g′(x)在區(qū)間[0,1]上遞增.

因此,當x∈[0,1]時,g′(x)∈[1-2a,e-2a].

所以函數(shù)g(x)在區(qū)間[0,ln(2a))上單調遞減,在區(qū)間(ln(2a),1]上單調遞增,于是g(x)在[0,1]上的最小值是g(ln(2a))=2a-2aln(2a)-b.

綜上,當a≤1/2時,g(x)在[0,1]上的最小值是g(0)=1-b; 當1/2

(2) 充分關注函數(shù)f(x)在區(qū)間(0,1)內有零點的條件,并結合對函數(shù)f(x)在區(qū)間[0,1]的兩端點處函數(shù)值以及g(x)=f′(x)在區(qū)間(0,1)內零點個數(shù)的分析,即可完成不等式的證明.

事實上,設x0為f(x)在區(qū)間(0,1)內的1個零點,則由f(0)=f(x0)=0可知f(x)在區(qū)間(0,x0)上不可能單調遞增,也不可能單調遞減,則g(x)=f′(x)不可能恒為正,也不可能恒為負,即g(x)在(0,x0)內有正有負.故g(x)在區(qū)間(0,x0)內必存在零點,記作x1.

同理由f(x0)=f(1)=0可知g(x)在區(qū)間(x0,1)內必存在零點x2,所以g(x)在區(qū)間(0,1)內至少有2個零點.

因此x1∈[0,ln(2a)],x2∈(ln(2a),1],并且必有g(0)=1-b>0,g(1)=e-2a-b>0.由f(1)=e-a-b-1=0,得-b=a-e+1,于是

g(0)=1-b=1+(a-e+1)=a-e+2>0,

g(1)=e-2a-b=e-2a+(a-e+1)=1-a>0.

解得e-2

函數(shù)的零點、方程的根以及函數(shù)的圖象與x軸交點或2個函數(shù)圖象的交點問題,本質上是同一類問題,歸根結底是函數(shù)的圖象與函數(shù)的性質問題.利用導數(shù)研究函數(shù)的零點,一方面可以通過研究函數(shù)的單調性,并結合函數(shù)零點的存在定理來解決,另一方面也可以把問題轉化為函數(shù)圖象的交點問題,利用數(shù)形結合思想來解決.

(作者單位：北京陳經(jīng)綸中學)