基于ADINA的樁土相互作用分析
崔春義 孟坤 程學磊 楊剛
摘要:基于大型通用數值計算平臺ADINA建立三維數值模型,分別結合相互作用三維接觸模型和p-y曲線簡化分析模型模擬樁土系統在水平荷載作用下的樁頂位移變化規律,計算分析表明:計算結果與實際測量值基本一致,驗證了兩種建模方式的合理性和正確性。在此基礎上進一步對p-y,曲線簡化分析模型在不同水平荷載作用下的工作性狀進行分析,計算結果表明p-y,曲線簡化分析模型能較好地模擬樁土間的相互作用行為,將其應用到樁基相關抗震設計中能明顯減少計算求解消耗。
關鍵詞:ADINA;樁土相互作用;p-y曲線;三維數值分析
中圖分類號:TU391;TU293.5 文獻標識碼:A 文章編號:1000-0666(2016)01-0096-05
0 引言
樁土相互作用在橋梁抗震分析中占有非常重要的地位,地震作用通過土運動將橫向荷載傳給樁基,分析水平荷載作用下樁土相互作用對橋梁抗震設計具有一定的指導意義。
樁基水平承載力的計算方法主要有3種,分別是有限元方法、彈性分析法和地基反力法。地基反力法即溫克爾地基梁模型法(燕斌,2007),該法將樁視為埋置于土介質中的梁,樁周土體用相互獨立的彈簧和阻尼器來表示,在考慮土抗力沿深度的變化同時還可以考慮土的非線性性質,但忽略了土的連續性。這一方法物理概念清晰,計算工作量少,在地基的設計和分析中被廣泛地應用。
地基反力法中p-y曲線法是在水平力作用下,地面下深度z處的土抗力P與該點的撓度y之間的關系曲線,綜合反映了樁周土的非線性,樁的剛度和外荷載作用性質等特點(肖曉春等,2002)。
以往的研究工作中由于當時計算理論和硬件條件限制,諸多樁土相互作用分析都對地基模型進行線性簡化處理,或利用二維模型進行簡化分析。本文將采用大型通用數值分析平臺ADINA,對橫向荷載作用下的樁土相互作用進行三維數值模擬,分析其在水平荷載作用下樁頂的最大位移。然后根據API規范規定的P-y曲線,用非線性彈簧模擬樁土的相互作用,建立樁土相互作用的簡化分析模型,將其在水平荷載作用下的樁頂位移與三維數值模型以及實際測定值之間進行比較,說明API規范規定的p-y曲線的適用性。將p-y曲線簡化分析方法應用到大型橋梁的抗震分析中,在保證計算精度的前提下能大大減少計算量,具有非常重要的工程實際意義。
1 數值分析模型
本文采用ADINA中的摩爾一庫倫材料模擬土體。庫倫摩擦定律是土力學中的一個基本定律,按照這個定律,破壞面上剪切應力τf與法向應力σf之間滿足下列關系式:
τf=c+σftanφ. (1)式中,c為黏聚力,φ為內摩擦角。
用摩爾應力圓表示,上述條件相當于破壞應力圓將與一條稱為強度包線的直線相切。用主應力表示,式(1)可改寫為將上述摩爾-庫倫強度理論推廣于塑性應變理論,即假定屈服條件也不受中主應力的影響。具有這種性質的材料稱為摩爾-庫倫材料(劉成宇,華祖餛,2009)。
三維樁土數值模型的參數設置如下:樁周土范圍取樁半徑的20倍,很多理論分析和計算結果證明了當樁周土范圍足夠大時其邊界對樁身位移的影響非常小,因此取邊界條件為:模型底部以及樁周土均采用全約束(袁志林等,2011)。
考慮到模型的對稱性,只建立一半的真實模型,所有對稱面在外法線上的位移是約束的,但在對稱面上可以自由移動,采用對稱約束,模型頂面上所有節點在各個方向上都是自由的。
本文使用試樁資料來自江蘇鎮江大港(1982)地區的試驗(陳洪,2004),試樁基本資料如表1所示,地質資料如圖1所示。
在模型中,樁體和土體采用8節點實體單元,用各項同性模型進行模擬。土體的變形包括彈性應變和塑性應變,是一種典型的彈塑性介質。土體的材料特性復雜、種類繁多,根據已知土體的不同參數,所對應的本構模型也有所不同,計算結果存在差異。因此模擬樁土間的相互作用時恰當地選取土體的本構模型,對于整個數值分析過程非常重要(李海林,2006)。目前應用比較多的是摩爾一庫倫材料,在ADINA中用摩爾一庫倫材料模擬土體,各個土層的屬性根據圖1中的各層地質資料進行輸入。
在ADINA中通過建立接觸對模擬樁土間的相互作用,首先在樁土界面上建立接觸面,然后建立相互對應的接觸對。接觸對中接觸面的選擇需要滿足一定的原則,即選擇剛度大、自由度相對較少的面即樁表面為Target Surface,土體剛度較小自由度相對較多為Contaetor Surface。樁土之間的庫倫摩擦系數取為0.2(周月慧等,2007)。建立的三維有限元模型如圖2所示。
2 p-y曲線簡化分析模型
根據API規范中規定的軟粘土的p-y曲線公式,計算出單位樁長的極限土抗力為式中,y為由地面到深度z處的土的平均有效重度;cu為土的不排水抗剪強度;z為土的深度;d為樁的邊寬或直徑;J為實驗系數,一般J=1/2,較硬的土取J=0.25。
土阻力達到極限土阻力一半時的相應變位為式中,y50為被動側土達到極限水平抗力的一半時相應深度處樁的側向變形(胡勝剛,2005);ε50為約一半的最大主應力差時的土的應變值,按表2取值。
樁徑d計算值(徐鵬舉等,2010)按下面方法求得:(1)圓形截面樁:實際樁徑D>1m時,取d=0.9(1+D);實際樁徑D≤1m時,取d=0.9(0.5+1.5D)。(2)方形截面樁:實際樁寬B>1m時,計算樁寬取d=B+1;實際樁寬B≤1m時,取d=1.5B+0.5。
由此確定p-y曲線為當y=8y50時,土達到p/pu=1的極限,此后保持為定值。軟粘土的p-y曲線如圖3所示。
根據計算出的p-y曲線,轉化出力與位移之間關系的具體數值,輸入ADINA中,生成非線性彈簧,模擬樁土之間的相互作用。
樁體采用二維梁單元模擬,樁底為固定約束,樁土之間的相互作用通過p-y曲線生成的非線性彈簧來模擬。模型總共設置了15個彈簧單元,在樁上節點與大地之間設置彈簧,計算模型如圖4所示:
3 計算結果分析
3.1 P-y曲線對比分析
按照試樁試驗的加載方式,在有限元計算中,同樣施加49.0kN、98.0kN、147.1kN、196.1kN和245.2kN的橫向水平荷載,計算得出樁頂水平位移。
由計算結果可知,三維數值分析模型計算的樁頂水平位移更接近實測位移,計算結果較p-y曲線簡化分析模型計算得出的樁頂水平位移小。三維模型計算結果差異性產生的原因主要有:三維分析模型土體本構關系的選取與實際土體存在一定的差異,接觸面相關參數的選取同樣會影響計算結果。
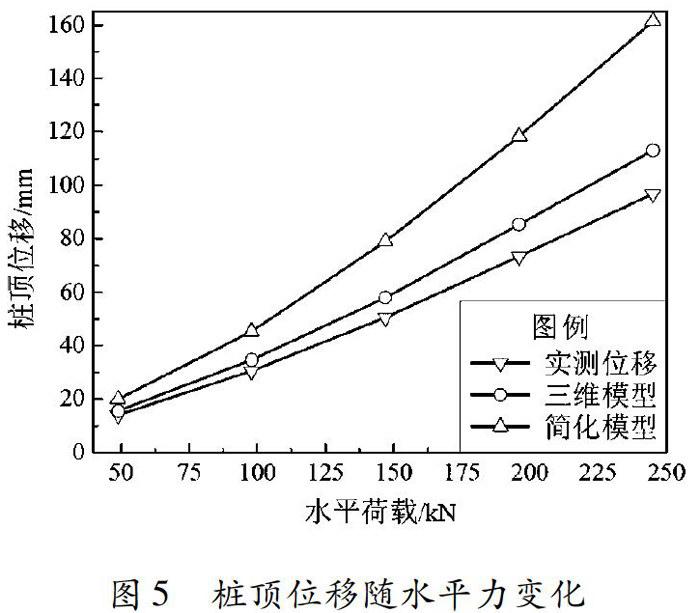
鎮江大港試樁在各級荷載作用下樁頂水平位移的實測值與三維數值模型和P-y曲線簡化分析模型計算結果的比較如表3所示。鎮江大港樁頂位移隨水平力變化如圖5所示。
隨荷載的增大p-y曲線模型的計算結果誤差也越來越大,造成這一結果的原因主要有:非線性彈簧模擬樁土間相互作用本身的近似性因素(李煒等,2011),同時所采用的P-y曲線是根據美國Austin地區的試驗資料構造,應用到其他地區會存在一定的誤差(曹維科,2011)。因此想要更好地應用p-y曲線簡化模型模擬樁土之間相互作用,必須根據試樁所在地的地質資料,尋找適合本地區的p-y曲線。
3.2 樁身變形分析
樁受到橫向荷載作用時,樁身的變形主要為水平向的撓曲。在不同水平向荷載作用下樁土相互作用的P-y曲線簡化分析模型中樁身的水平位移沿埋深的變化如圖6所示。由圖6可知,隨著荷載的逐漸增大樁身位移越來越大,荷載增大到一定程度之后,樁頂的位移增大幅度呈增長趨勢。樁身位移沿埋深的變化充分說明了樁土之間相互作用的非線性,當荷載增到一定程度之后,樁逐漸達到極限狀態,趨于破壞,樁頂位移急劇增大。
樁在49.0kN、147.1kN、245.2kN水平荷載作用下的樁身變形如圖7所示,可以看出,樁頂位移隨荷載的增大而增大,埋深達到15m后,樁身位移隨荷載增大變化并不明顯。樁身位移在樁頂處達到最大值,然后沿樁深逐漸減小,到樁體位移為零后,樁體位移開始反向增大,增大到一定值后又開始減小,到樁底時位移為零,很符合柔性長樁的特性(劉延芳,2014)。
4 結論
采用大型通用數值分析平臺ADINA對水平荷載作用下樁基的工作性狀進行分析,分別建立了橫向荷載作用下的樁土相互作用三維有限元數值分析模型與p-y曲線簡化分析模型。計算分析表明:
(1)三維有限元數值分析模型所得的計算結果與實際測量的結果基本一致,而應用API規范中規定的p-y曲線計算的樁頂位移與實測值之間相差較大,說明API規范中規定的p-y曲線有一定的局限性,只適用于與Austin地區地質情況大致相同的地區。
(2)p-y曲線模擬樁土間相互作用簡化分析模型在不同水平荷載作用下的工作性狀進行分析,計算結果與樁基實際受力性能基本一致,說明p-y曲線能較好地模擬樁土間的相互作用。這樣,應用P-y曲線法須先根據本地區的地質資料由實驗或者三維分析的方法求得適合本地區的p-y曲線。
(3)在保證計算精度的前提下,將P-y曲線模擬樁土間相互作用的簡化計算方法應用到樁基抗震設計中能大大減少計算消耗,具有非常重要的工程現實意義。