某復(fù)雜構(gòu)型飛機偏航－滾轉(zhuǎn)耦合運動非定常氣動力特性實驗研究

楊 文，卜 忱，眭建軍

某復(fù)雜構(gòu)型飛機偏航－滾轉(zhuǎn)耦合運動非定常氣動力特性實驗研究

楊 文＊，卜 忱，眭建軍

（中航工業(yè)空氣動力研究院，哈爾濱 150001）

摘要：在FL－8風(fēng)洞中設(shè)計并制造了一套雙自由度大幅振蕩實驗系統(tǒng)，不僅能模擬飛機單自由度機動歷程，還能實現(xiàn)模型繞體軸的偏航－滾轉(zhuǎn)耦合運動及俯仰－滾轉(zhuǎn)耦合運動。本文通過適當(dāng)?shù)膶嶒炘O(shè)計，基于運動時間歷程的影響分析，在振蕩平衡位置定量地研究耦合因素對偏航－滾轉(zhuǎn)耦合振蕩運動中非定常氣動力特性的影響。結(jié)果表明，當(dāng)振蕩運動平衡位置迎角遠小于失速迎角時，偏航－滾轉(zhuǎn)耦合運動的氣動力等于單自由度運動相應(yīng)氣動力的線性疊加，平衡位置迎角在失速迎角附近時，非定常氣動特性受耦合因素影響顯著，而平衡位置迎角在遠大于失速迎角時，非定常氣動特性受耦合因素影響變小，但仍然較大。
關(guān)鍵詞：FL－8風(fēng)洞；大振幅；非定常氣動力；時間歷程；耦合振蕩
中圖分類號：V211.71文獻標(biāo)識碼：A

0 引 言

飛機大迎角下的高機動性是現(xiàn)代戰(zhàn)斗機的一項重要戰(zhàn)術(shù)指標(biāo)，這就要求飛機設(shè)計人員能夠提供足夠準確的大迎角機動飛行中的非定常空氣動力數(shù)據(jù)。由于飛機機動飛行的運動過程很復(fù)雜，在風(fēng)洞中準確模擬飛機機動飛行并測量其氣動力顯得十分重要。對于簡單的機動飛行，如眼鏡蛇機動［1－2］、機翼搖滾［3－4］等，風(fēng)洞模擬相對容易，目前國內(nèi)外許多風(fēng)洞已經(jīng)設(shè)計了實驗裝置并進行了一系列的實驗［5－8］。而對于復(fù)雜的機動飛行，如Herbst機動［9］等，飛機在大迎角狀態(tài)下為同時繞幾個軸的耦合運動。實際上，Herbst機動就是飛機在快速拉起到大迎角時進行無側(cè)滑或小側(cè)滑狀態(tài)下的偏航與滾轉(zhuǎn)耦合運動，這類機動飛行方式很有實戰(zhàn)意義。事實上，有些飛行力學(xué)的研究者也提出了同樣的研究課題，例如美國的Zhongjun W［10］等人在F－16XL飛機的飛行特性模擬計算與飛行實驗結(jié)果的對比時，提出了需要獲得橫航向耦合運動非定常空氣動力參數(shù)的必要性。在國內(nèi)，南京航空航天大學(xué)的黃達［11－12］等人在偏航－滾轉(zhuǎn)耦合運動的非定常氣動力特性研究中做了大量卓有成效的工作，在這些文獻中主要定性地研究了耦合運動與單自由度運動的遲滯特性的異同。本文將在此研究的基礎(chǔ)上，從單自由度的氣動力時間歷程效應(yīng)分析出發(fā)，通過適當(dāng)?shù)膶嶒灧桨冈O(shè)計，嘗試在耦合運動和單自由度運動的各狀態(tài)變量一致的情況下，定量地研究耦合特性的具體影響量，并得到更加可靠的結(jié)論，為耦合運動的非定常氣動力建模提供依據(jù)。

1 實驗設(shè)備和模型

1.1雙自由度大幅振蕩機構(gòu)

本次實驗是在中航工業(yè)空氣動力研究院FL－8回流式閉口低速風(fēng)洞中進行的，風(fēng)洞實驗段長5.5m，截面尺寸3.5m×2.5m，空風(fēng)洞最大風(fēng)速72m／s。動態(tài)實驗平臺為新改造設(shè)計的雙自由度大幅振蕩實驗系統(tǒng)。圖1為雙自由度振蕩系統(tǒng)結(jié)構(gòu)，模型正裝時液壓馬達驅(qū)動彎刀使模型做俯仰運動，而當(dāng)模型側(cè)裝時即可實現(xiàn)偏航振蕩運動，伺服電機能夠驅(qū)動模型做滾轉(zhuǎn)振蕩，運動過程中，模型的實際迎角和側(cè)滑角可以通過機構(gòu)角轉(zhuǎn)換得到。

式中：θ為平臺轉(zhuǎn)盤角，φ為大彎刀轉(zhuǎn)角，而是尾撐支桿滾轉(zhuǎn)角。圖2為某飛機大幅振蕩實驗照片，模型采用尾撐。

圖1 雙自由度振蕩系統(tǒng)結(jié)構(gòu)示意圖Fig.1 Structure diagram of coupling oscillation system

圖2 大幅振蕩實驗照片F(xiàn)ig.2 Picture for large amplitude oscillation test

1.2測控系統(tǒng)及數(shù)據(jù)處理系統(tǒng)

實驗采用動態(tài)專用六分量內(nèi)式天平，天平測得的電信號由FL－8風(fēng)洞VXI采集系統(tǒng)采集，數(shù)字信號由工控機處理，實驗原始數(shù)據(jù)由大幅振蕩實驗處理程序處理成體軸六分量系數(shù)。動態(tài)濾波采用傅里葉變換數(shù)字濾波器，實驗現(xiàn)場可以實時顯示曲線。

2 實驗結(jié)果和分析

2.1時間歷程影響研究

考慮到模型在大振幅強迫振蕩時，其姿態(tài)角及角速率始終在變化中，為了獲得單純的時間歷程影響，需保證這些狀態(tài)變量都一致，而僅僅運動歷程不同。現(xiàn)以單自由度滾轉(zhuǎn)振蕩的滾轉(zhuǎn)力矩系數(shù)為例加以說明。為了研究時間歷程的影響，本文進行了表1中所描述狀態(tài)的滾轉(zhuǎn)振蕩試驗，需要說明的是表1中分別在10°、20°、30°及40°共4個振蕩平衡位置迎角處各自進行4個不同振幅和頻率的振蕩實驗，總共有16次實驗。從表1可知，在每個振蕩平衡位置迎角處，不同振幅、頻率組合狀態(tài)下，迎角、側(cè)滑角、滾轉(zhuǎn)角及滾轉(zhuǎn)角速度等位移和運動速度變量均相同，唯一不同的是其前一時間段位移和運動速度，即時間歷程不同，因而模型在振蕩平衡位置處的前一時刻氣動力特性不同。基于此，通過分析各振蕩平衡位置迎角處不同運動狀態(tài)的氣動力特性差異就可以研究在不同迎角范圍氣動力的時間歷程影響。圖3～6給出了不同振蕩平衡位置迎角處的時間歷程影響實驗結(jié)果。在圖3和4中，靜態(tài)氣動力系數(shù)曲線基本在動態(tài)遲滯環(huán)中間，且隨著位移向平衡位置靠近，非定常氣動力增量逐漸變大，且各運動狀態(tài)在振蕩平衡位置處非定常氣動力增量基本相等，又因為平衡位置處各運動狀態(tài)的位移和運動速度矢量相同，因此，在小迎角時滾轉(zhuǎn)振蕩運動的時間歷程影響較小。這可能是因為在小迎角下，雖然左右機翼翼面流場結(jié)構(gòu)的變化相對于翼面本身的運動仍然存在遲滯現(xiàn)象，但對于前機身帶邊條翼的戰(zhàn)斗機布局在較小迎角處流場始終是脫體渦結(jié)構(gòu)，沒有出現(xiàn)渦的破裂，因而非定常氣動力增量僅是角速度引起的，并不會出現(xiàn)非線性遲滯增量，所以在振蕩平衡位置處滾轉(zhuǎn)角速度相同時時間歷程的影響較小。然而，如圖5和6所示，振蕩平衡位置迎角在30°和40°時，靜態(tài)氣動力曲線并不在動態(tài)遲滯環(huán)中間，甚至跳出了遲滯環(huán)。且各運動狀態(tài)下，非定常氣動力增量差值明顯，又因為平衡位置處位移和運動速度等變量相同，因而時間歷程對氣動特性的影響顯著增大。原因可能是：30°迎角后，在大幅滾轉(zhuǎn)振蕩過程中，左右機翼的當(dāng)?shù)赜强缍容^大且經(jīng)過失速迎角區(qū)域，此時機翼表面流場不僅相對于翼表本身運動遲滯，而且流場結(jié)構(gòu)也在發(fā)生變化，這種脫體渦的破裂與再附的遲滯將會引起極大的非線性非定常氣動力增量。需要說明的是，圖6中由于各狀態(tài)下的氣動力遲滯環(huán)出現(xiàn)交叉，因而振蕩平衡位置處非定常氣動力增量的差別沒有圖5中明顯，但由于各自交叉次數(shù)不同，在振蕩平衡位置處遲滯環(huán)方向就不同，即滾轉(zhuǎn)阻尼特性不同，說明此時運動歷程的影響可能更復(fù)雜。

表1 實驗參數(shù)Table 1 Experimental parameters

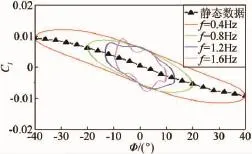
圖3 滾轉(zhuǎn)運動在平衡位置為迎角10°時的時間歷程影響Fig.3 The time history influence at equilibrium position ofα＝10°for roll oscillation

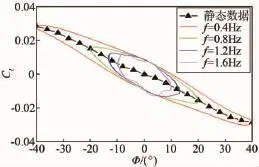
圖4 滾轉(zhuǎn)運動在平衡位置為迎角20°時的時間歷程影響Fig.4 The time history influence at equilibrium position ofα＝20°for roll oscillation

圖5 滾轉(zhuǎn)運動在平衡位置為迎角30°時的時間歷程影響Fig.5 The time history influence at equilibrium position ofα＝30°for roll oscillation

圖6 滾轉(zhuǎn)運動在平衡位置為迎角40°時的時間歷程影響Fig.6 The time history influence at equilibrium position ofα＝40°for roll oscillation

偏航振蕩運動和耦合運動的時間歷程影響和滾轉(zhuǎn)運動類似，如圖7所示，給出了偏航振蕩運動在振蕩平衡位置迎角30°時的歷程影響曲線。

圖7 偏航振蕩運動在平衡位置為迎角30°時的時間歷程影響Fig.7 The time history influence at equilibrium position ofα＝30°for yaw oscillation

2.2雙自由度運動中耦合因素影響研究

本次實驗在模型振蕩平衡迎角0°～90°范圍內(nèi)開展研究，單自由度滾轉(zhuǎn)振蕩、偏航振蕩及偏航－滾轉(zhuǎn)耦合振蕩的振幅均為40°、頻率相同，這樣在振蕩平衡位置處耦合運動與相應(yīng)的單自由度運動的狀態(tài)變量相同，不同的是時間歷程和耦合因素，表2給出了各振蕩模態(tài)的實驗參數(shù)變量，2.1節(jié)已經(jīng)分析了各運動模態(tài)的時間歷程影響，現(xiàn)只需對比耦合運動與單自由度運動氣動力，便可比較直觀地研究雙自由度運動中耦合因素的影響。

表2 實驗參數(shù)Table 2 Experimental parameters

先引入幾個簡單的氣動力模型表達式并以滾轉(zhuǎn)力矩系數(shù)為例加以說明。忽略角加速度的影響，僅考慮迎角α、側(cè)滑角β、側(cè)滑角速率β·及滾轉(zhuǎn)角速度p和偏航角速度r的影響。單自由度滾轉(zhuǎn)振蕩時，將振蕩平衡位置的滾轉(zhuǎn)力矩系數(shù)分解為靜態(tài)氣動力矩及由滾轉(zhuǎn)角速度和側(cè)滑角速率β·引起的增量；而單自由度偏航振蕩時，相應(yīng)地分解為靜態(tài)氣動力矩及由偏航角速度r和側(cè)滑角速率β·引起的增量。不論是單自由度滾轉(zhuǎn)振蕩，還是單自由度偏航振蕩，其β·不是獨立的，且分別和p、r相關(guān)，在振蕩運動的平衡位置處相關(guān)公式如下：

公式（6）中β·C表征耦合振蕩平衡位置處的側(cè)滑角速率，對公式（1）中的第2式求導(dǎo)可得：

在耦合振蕩運動的平衡位置處，β＝0、＝0且φ＝0，則公式（7）簡化為：

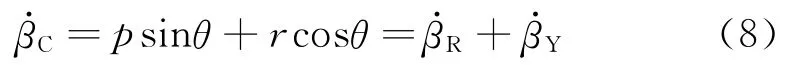
從公式（8）中可知，在振蕩平衡位置處，耦合運動的側(cè)滑角速率等于各單自由度振蕩運動側(cè)滑角速率的線性疊加。在耦合運動的平衡位置處，繞體軸的角速度p、r及側(cè)滑角速率β·均等于單自由度相應(yīng)變量的線性疊加。

若耦合振蕩氣動力特性也是線性疊加的，則振蕩平衡位置的滾轉(zhuǎn)力矩元表達式如下：

單自由度及耦合振蕩運動的平衡位置姿態(tài)角α和β相同，則Cl0（α，β）理論上應(yīng)該相等，這里令：

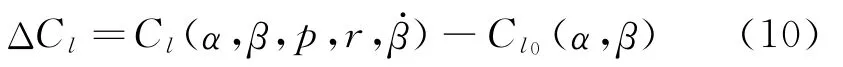
比較表達式（6）和（9）中該滾轉(zhuǎn)力矩系數(shù)差量ΔCl隨迎角α的變化規(guī)律。實驗結(jié)果在圖8（a）中給出。

圖8 耦合運動與單自由度疊加氣動力特性比較Fig.8 Comparison of unsteady aerodynamic between coupling movement and sum of single degree of freedom movements

圖8 （a）中對應(yīng)的各模態(tài)振蕩頻率均為0.6Hz且振幅為40°時，圖中橫坐標(biāo)的迎角是各振蕩運動平衡位置處的迎角。在20°迎角前，耦合運動滾轉(zhuǎn)力矩系數(shù)幾乎等于單自由度運動相應(yīng)系數(shù)的線性疊加，由前時間歷程的影響分析可知，在此迎角范圍內(nèi)，不同歷程的影響較小。因此，在小迎角時，對于偏航－滾轉(zhuǎn)耦合運動，耦合因素并沒有帶來滾轉(zhuǎn)氣動力系數(shù)的變化。這可能是因為：在小迎角耦合運動過程中，左右機翼的當(dāng)?shù)赜强缍炔淮螅砻娴拿擉w渦流雖然相對于運動本身有遲滯，但流場結(jié)構(gòu)并沒有發(fā)生變化，這時氣動力動態(tài)增量僅僅與位移矢量和運動速度相關(guān)，在振蕩平衡位置處，耦合運動的位置矢量和速度矢量等于各單自由度運動的線性疊加，因而滾轉(zhuǎn)氣動力模型完全可以分解成相應(yīng)的單自由度運動氣動力模型的線性疊加。當(dāng)迎角達到20°后，隨著迎角的增加，耦合運動滾轉(zhuǎn)力矩系數(shù)增量與單自由度運動疊加的差值愈來愈大，在30°～35°迎角附近，耦合運動滾轉(zhuǎn)力矩系數(shù)動態(tài)增量大小與相應(yīng)單自由度運動疊加相差最大。這可能是因為：振蕩平衡位置迎角達到30°后，在耦合運動過程中，左右機翼當(dāng)?shù)赜窃谑儆歉浇兓浔砻鏈u流結(jié)構(gòu)在后緣處出現(xiàn)渦破裂，這種渦的破裂和再附的遲滯將帶來極大的非定常氣動力增量，且該增量不僅與飛機的運動位置矢量和速度矢量相關(guān)，還和時間歷程及耦合因素緊密相關(guān)，因而即使在振蕩平衡位置處耦合運動和各單自由度運動的位置矢量、速度矢量相等，其非定常氣動力增量仍然存在較大差值。上述分析說明，在失速迎角附近的中等迎角處，由于其時間歷程及耦合特性影響顯著，耦合運動已經(jīng)不能簡單地分解成相應(yīng)的單自由度運動疊加。因此，此時在建立非定常氣動力模型時不僅僅需要考慮各單自由度運動的氣動力模型，還需要添加耦合項的綜合影響。迎角40°后，隨著迎角的增加，耦合運動滾轉(zhuǎn)力矩系數(shù)動態(tài)增量大小與相應(yīng)單自由度運動疊加的差值雖有變小，但仍然較大，特別是當(dāng)迎角達到60°后趨于一個穩(wěn)定差值。這說明在遠超失速迎角的范圍，飛機運動的時間歷程及耦合特性影響仍然較大。圖8（b）和（c）中描述的偏航力矩系數(shù)與側(cè)力系數(shù)的變化規(guī)律和滾轉(zhuǎn)力矩系數(shù)類似。

3 結(jié) 論

本文的研究結(jié)論主要有以下2點：

（1）對于單自由度滾轉(zhuǎn)振蕩，小迎角時，滾轉(zhuǎn)力矩受時間歷程影響較小。因此，此時的氣動力模型只需考慮飛機的瞬時運動狀態(tài)變量；而在30°迎角后，其受時間歷程的影響顯著。單自由度偏航振蕩，其時間歷程的影響規(guī)律類似。

（2）在20°迎角前，耦合運動橫航向力矩模型完全可以分解成相應(yīng)的單自由度運動氣動力模型的線性疊加；在失速附近的中等迎角區(qū)域，運動耦合及時間歷程對力矩特性影響顯著；而在60°后的大迎角區(qū)域，耦合的影響雖然減小，但仍然很大。

本文雖然對偏航－滾轉(zhuǎn)耦合運動非定常氣動力增量與各單自由度運動的增量線性疊加進行了比較，并分析了可能的原因，但也僅僅是氣動力結(jié)果，下一步工作還需對耦合運動過程中的流場結(jié)構(gòu)機理開展研究，特別是渦破裂點的變化規(guī)律研究。

［1］李中華.Su－27飛機眼鏡蛇機動及其戰(zhàn)術(shù)意義［J］.飛行力學(xué)，2000，18（1）：54－57.Li Z H.Su－27Cobra maneuver and its tactical application［J］.Flight Dynamics，2000，18（1）：54－57.

［2］高慧琴，高正紅.典型過失速機動運動規(guī)律建模研究［J］.飛行力學(xué)，2009，27（4）：9－13.Gao H Q，Gao Z H.Motion modeling of typical post stall maneuvers［J］.Flight Dynamics，2009，27（4）：9－13.

［3］Ericsson L E.Wing rock generated by forebody vortices［R］.AIAA－87－0268，1987.

［4］Pelletier Alain.Dynamic behavior of an 80／65double－delta wing in roll［R］.AIAA－98－4353，1998.

［5］Brandon J M，Shah G H.Unsteady aerodynamic characteristics of fighter model undergoing large－amplitude pitching motions at high angles of attack［R］.AIAA－90－0309，1990.

［6］Jay M Brandon，Mark A.Overview of dynamic test techniques for flight dynamics research at NASA LaRC（Invited）［R］.AIAA－2006－3146，2006.

［7］William J G.AFRL F－22dynamic wind tunnel test result［R］.AIAA－99－4015，1999.

［8］卜忱，杜希奇，黃麗婧，等.旋轉(zhuǎn)流場下飛機大幅滾轉(zhuǎn)振蕩時的動態(tài)橫向氣動特性實驗研究［J］.實驗流體力學(xué)，2008，22（1）：46－50.Bu C，Du X Q，Huang L J，et al.Investigation of unsteady aerodynamic characteristics for the large amplitude rolling under rotary flow field［J］.Journal of Experiments in Fluid Mechanics，2008，22（1）：46－50.

［9］Michael C，F(xiàn)rancis S.X－31enhanced fighter maneuverability demonstrator fight test achievements［R］.ICAS－94－72，1994.

［10］Zhongjun W，Edward C L.Unsteady aerodynamic effects on the flight characteristics of a F－16XL configuration［R］.AIAA－2000－39，2000.

［11］黃達，吳根興.飛機偏航－滾轉(zhuǎn)耦合運動非定常空氣動力實驗［J］.南京航空航天大學(xué)學(xué)報，2005，37（4）：408－411.Huang D，Wu G X.Experiment on fighter oscillating in large amplitude yaw－roll motion［J］.Journal of Nanjing University of Aeronautics and Astronautics，2005，37（4）：408－411.

［12］黃達.飛行器大幅振蕩運動非定常空氣動力特性研究［D］.南京：南京航空航天大學(xué)，2007.Huang D.Unsteady aerodynamic characteristics for the aircraft oscilation in large amplitude［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2007.

Investigation of the unsteady aerodynamic characteristics of a fighter with complex configuration undergoing yaw－roll coupling oscillation motion

Yang Wen＊，Bu Chen，Sui Jianjun
（Aerodynamics Research Institute of Aviation Industry Corporation of China，Harbin 150001，China）

A new set of double degree of freedom in volatile test system is designed and constructed in FL－8wind tunnel.The test apparatus can not only simulate aircraft′s single degree of freedom maneuver，but also realize yaw－roll coupling movement and pitch－roll coupling movement around the body axis.This paper introduces the experimental project in detail and conducts research into the time history influence when the model is maneuvering.Afterwards the influence of the coupling factor on the unsteady aerodynamic characteristics undergoing yaw－roll coupling oscillation motion is analyzed quantitatively at the oscillation equilibrium position.The results indicate that the unsteady aerodynamic gained undergoing yaw－roll coupling oscillation motion is equal to the linear superposition of the unsteady aerodynamic gained in the test of single yaw and roll motions when the angle of attack at the equilibrium position is less than the stall angle of attack.The influence of the coupling factor on the unsteady aerodynamic is remarkable near the stall angle of attack.The influence of the coupling factor on the unsteady aerodynamic is weak when the angle of attack at the equilibrium position is much greater than the stall angle of attack.

FL－8wind tunnel；large amplitude；unsteady aerodynamic；time history；coupling oscillation

（編輯：張巧蕓）

1672－9897（2016）03－0061－05

10.11729／syltlx20150104

2015－07－30；

2015－12－18

＊通信作者E－mail：yangwen19860804＠163.com

Yang W，Bu C，Sui J J.Investigation of the unsteady aerodynamic characteristics of a fighter with complex configuration undergoing yawroll coupling oscillation motion.Journal of Experiments in Fluid Mechanics，2016，30（3）：61－65.楊文，卜忱，眭建軍.某復(fù)雜構(gòu)型飛機偏航－滾轉(zhuǎn)耦合運動非定常氣動力特性實驗研究.實驗流體力學(xué)，2016，30（3）：61－65.

楊文（1986－），男，湖南常德人，碩士，工程師。研究方向：風(fēng)洞動態(tài)試驗技術(shù)及非定常氣動力建模。通信地址：黑龍江省哈爾濱市88號信箱（150001）。E－mail：yangwen1986 0804＠163.com