基于影子軌跡線和相似原理的太陽影子定位技術研究

蔡俊浩 李洛勤 李繼昌 周益輝

摘 要：針對太陽影子定位技術，本文主要解決三個問題。（1）根據太陽照射下直桿成影的原理以及直桿影子隨著時間的變化規律，建立太陽點、時間和影子端點坐標的空間模型，求出直桿影子長度隨時間的變化規律。（2）根據兩個不等長的直桿在同一位置任意時間影子的長度之比為一恒定值這一原理求出該直桿所在的地點。（3）根據步驟2的原理以及一天中直桿影子長度的變化確定直桿所處的地點和日期。

關鍵詞：天體模型；經緯度；影子軌跡

在視頻數據分析中，如何來確定視頻的拍攝地點和拍攝日期是一個重要的分析方面，而其中一種重要技術就是利用太陽影子定位技術分析視頻中的問題的太陽影子變化。

1 直桿影子長度變化

在太陽的照射下，一天中直桿的影子的位置不是固定不變的，影子的位置會隨太陽的位置變化發生變化。若假設某一天當中的某一個時刻的太陽位置如圖1 所示，設直桿垂直于地面上的高度為H，太陽光線平行通過直桿頂端P點時在地面上形成的影子點為，且所形成的影子的長度為L，，則可得到：

在每一天中地球自轉一周是360°，每1h自轉的度數為15°， 且這個角度稱為時角（）。由于隨著地球的自轉及繞太陽公轉的不斷進行，太陽位置也隨著時間在不斷地發生變化 。因此，可以獲得不同時間點直桿頂端的落影點，并且由求出的各個時間點下的不同的直桿頂端落影點點形成一天中直桿頂端落影點的軌跡線。

2 基于相似三角形定理的影子地點確定

設定在同一地點有另外一個直桿，高度為，

而真實的直桿的高度為，設，為直桿之間的比例系數，根據相似三角形定理，我們可以得到，，因此可以得到

由上式看出，在同一日期同一地點，即使不同時刻不同長度的直桿的影子長度不同，他們之間的長度比值相同，而且比值是一個定值。

假設已知日期和直桿長度和某未知地點下一段時間的影子坐標的數據，根據此數據和上述分析，我們可以知道該地點在當天也有特定的比例系數。現在我們設定了一個網格坐標，坐標變量為經緯度，假設已經知道某個具體的經緯度，則可以通過上述模型求出在相同時間段下影子的長度變化，和附錄中給出的影子長度求比值。

式中，為各個比例系數的差分平方和，如果平方和值越小，則代表著誤差越小，說明該點越接近所在地點。如果誤差接近為0，則該點可以近似作為所求的地點。

3 基于相似三角形定理的地點和時間確定

由于日期未知，因此對于赤緯角而言也是一個未知量，因此可以再次考慮使用步驟二進行365次迭代，每次迭代帶入不同日期代表的赤緯角，通過遍歷之后找出當天的局部最優解，再從365天中再找出全局最優解，最后得到的天數和經緯度即為可能的地點和日期。由于模型的建立與步驟二的內容幾乎一樣，所以與步驟二的模型相同的內容則不再重復。模型的不同點如下：

其中day為一年365天中的第day天。

4 實驗結果

本次試驗采用2015高教社杯全國大學生數學建模競賽A題題目中提供的數據進行模型的驗證。

4.1 直桿影子長度變化

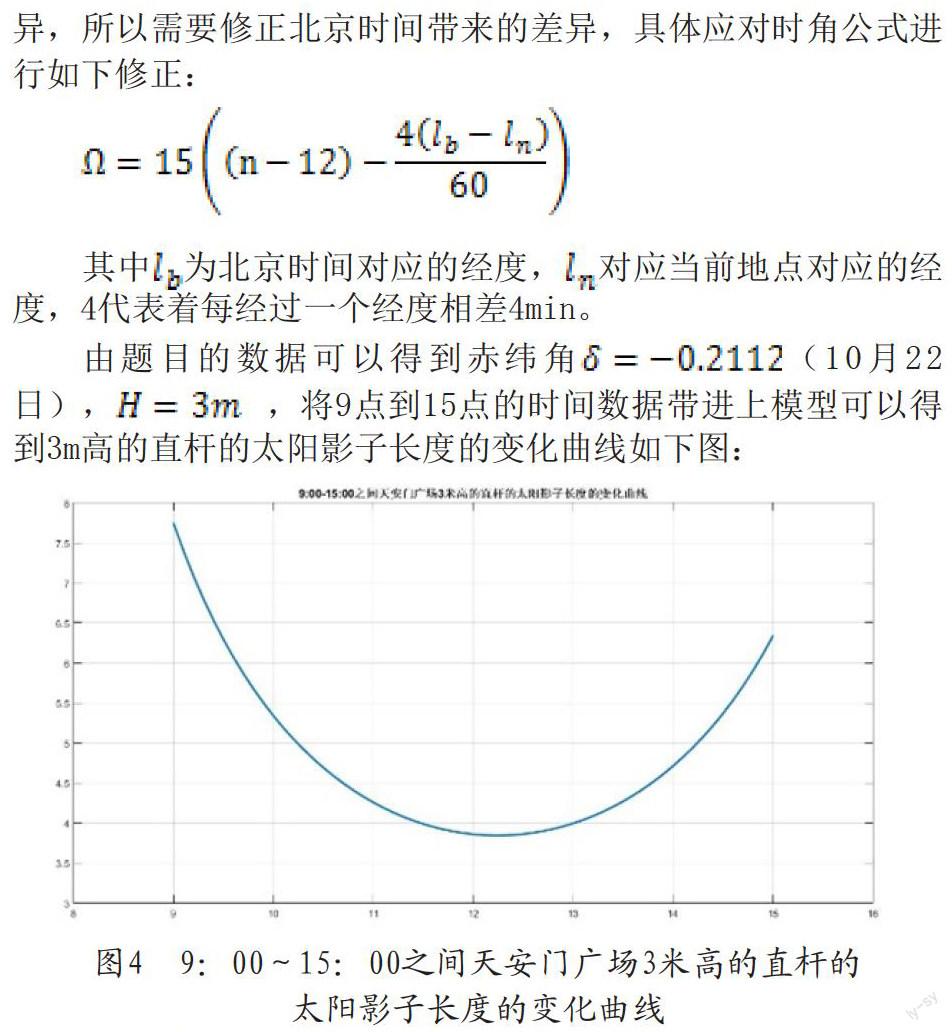
題目給出的經度為東經116°23′29″，而所參照的時間為北京時間（東經120度所對應的時間），在時間上有所差異，所以需要修正北京時間帶來的差異，具體應對時角公式進行如下修正：

其中為北京時間對應的經度，對應當前地點對應的經度，4代表著每經過一個經度相差4min。

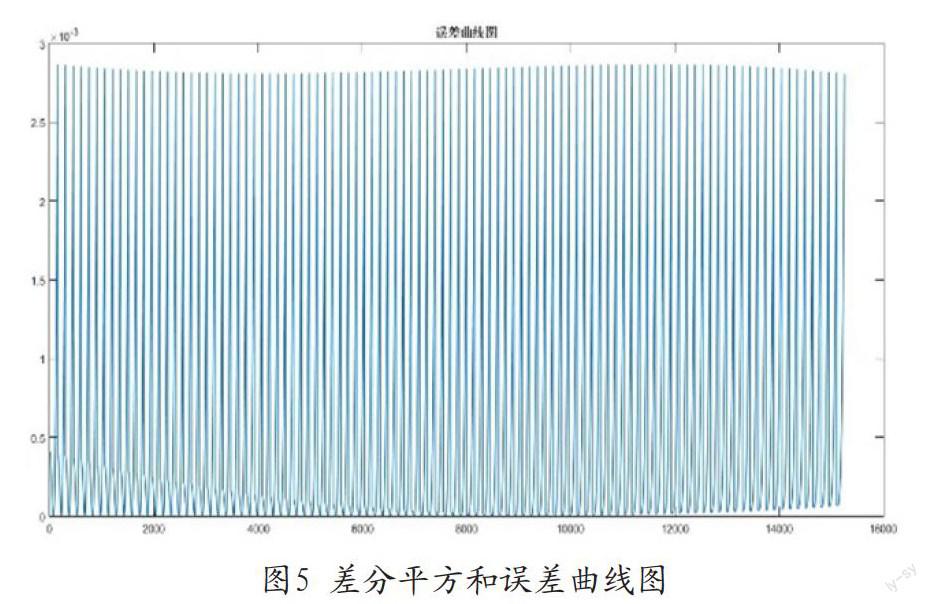
由題目的數據可以得到赤緯角（10月22日）， ，將9點到15點的時間數據帶進上模型可以得到3m高的直桿的太陽影子長度的變化曲線如下圖：

4.2 基于相似三角形定理的影子地點確定

通過觀察數據可以得到該時間段影子的長度呈遞增現象，因此首先對數據中的影子長度求差分，得到影子在不同時刻的變化率，再通過曲線的多項式擬合可以初步的得到變化率為0時的點，該點既可以認為是當地時間12點時所對應的點，由此可以通過地理知識在該點時間與北京時間的差異上求出大概的經度位置。

經過上面經度的預處理我們以107.4375為核心左右20度進行搜索，得到如下誤差曲線：

求得最優位置的經緯度為：東經108.8000，北緯19.2000，誤差平方和error=3.66942e-08，可以近似為0；經查閱地圖，該點為中國海南省的某個位置。

參考文獻

[1]鄭鵬飛，林大鈞，劉小羊，等.基于影子軌跡線反求采光效果的技術研究[J]. 華東理工大學學報（自然科學版），2010，（3）：458-463.

[2]蔣洪力.太陽直射點緯度的數學推導和分析[J].數學通報，2007，（9）：39-40.

[3]肖智勇，劉宇翔.一種新的緯度測量方法[J].大學物理，2010，（9）：51-54.

（作者單位：華南師范大學物理與電信工程學院）