卷積碼識別算法淺述

丁　嶠，徐　衛(wèi)

（1.解放軍理工大學(xué)，南京 210007；2.空軍通信網(wǎng)絡(luò)技術(shù)管理中心，北京 100843）

?

卷積碼識別算法淺述

丁嶠1，徐衛(wèi)2

（1.解放軍理工大學(xué)，南京 210007；2.空軍通信網(wǎng)絡(luò)技術(shù)管理中心，北京 100843）

摘要：本文介紹了信道編碼識別技術(shù)的發(fā)展概況，給出了常規(guī)識別算法、基于校驗矩陣識別算法和基于歐幾里德識別算法三種卷積碼識別算法的工作原理，對比分析了三種算法的性能。

關(guān)鍵詞：卷積碼；編碼識別；校驗矩陣；歐幾里德算法；算法性能

徐 衛(wèi)，空軍通信網(wǎng)絡(luò)技術(shù)管理中心高級工程師，主要從事通信網(wǎng)絡(luò)管理方面的技術(shù)工作。

1 引言

通信偵察使用專門的偵察設(shè)備搜索、截獲無線電通信信號，通過對信號進(jìn)行處理、分析和識別，從而獲取大量通信對抗情報，乃至重要的軍事情報。由于不同通信系統(tǒng)的業(yè)務(wù)要求和信道條件差異較大，因此，不同的通信系統(tǒng)通常采用不同的信道編碼方案，這對于諸如通信偵察這樣的非合作通信來說，要獲取無線電信號中所攜帶的信息，知道該信號所采用的信道編碼方案是其中的必要條件之一，編碼分析識別技術(shù)在通信偵察領(lǐng)域應(yīng)運而生。此外，編碼分析識別技術(shù)還可以應(yīng)用于未來智能通信領(lǐng)域、無線電監(jiān)測與管理等領(lǐng)域［1］。

2 信道編碼識別技術(shù)發(fā)展概況

當(dāng)前信道編碼分析識別技術(shù)研究主要集中在對線性分組碼和卷積碼的盲識別上。

二進(jìn)制線性分組碼的盲識別方法又可分為通過解線性方程來計算校驗多項式的識別方法和基于碼組正交空間的盲識別方法。利用低碼率二進(jìn)制線性分組碼的碼重分布特征來估計編碼參數(shù)［2］，數(shù)據(jù)矩陣求秩的方法在無誤碼情況下能夠準(zhǔn)確地估計出線性分組碼碼長、碼組偏差，但是當(dāng)誤碼率較高時，由于矩陣求秩的限制，不能有效估計出編碼參數(shù)，并且，當(dāng)碼長較長時，也不能有效估計出編碼參數(shù)。

RS碼的盲識別方法是基于伽羅華域傅立葉變換來實現(xiàn)的，它是利用RS碼在伽羅華域中的零譜連續(xù)特征求出碼根，得到編碼參數(shù)。卷積碼的盲識別方法可進(jìn)一步分為一般卷積碼的盲識別和刪除卷積碼的盲識別方法。當(dāng)前編碼盲識別技術(shù)尚處于發(fā)展中，仍存在許多局限和不足。本文主要介紹卷積碼的盲識別算法。

3 常見卷積碼識別算法

3.1 常規(guī)識別算法

進(jìn)行卷積碼識別最直接的算法是求解線性方程組。為敘述簡單，我們以碼率為 的卷積碼為例。設(shè)卷積碼是［4］

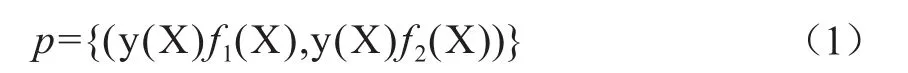
式中，y（X）=y0+y1X+y2X2+…，是信息源數(shù)據(jù)序列；f1（X）,f2（X）是生成多項式。p（X）=（p1（X）,p2（X））∈p，其中，pi（X）= pi , 0+ pi , 1X+ pi , 2X2+…，i = 1 , 2。該方法需要先估計約束長度L=max（degf1（X）,degf2（X））。如果能保證采集到的不含誤碼的卷積碼的片段序列足夠長N≥3（L+1），即要獲取的卷積碼碼流比特數(shù)大于2N=6（L+1），則可以求解如下的線性方程組：

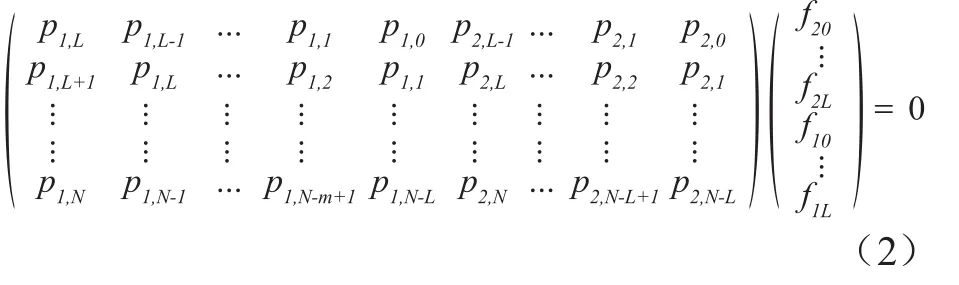
常規(guī)做法是高斯消元法，但是會存以下弊端：

首先，高斯消元法是不容錯的，即要求方程組（2）中的系數(shù)矩陣中的每個系數(shù)不能有錯誤。但在實際通信中，信道誤碼在所難免，采集到的數(shù)據(jù)很難保證沒有差錯。

其次，為保證方程組（2）的可解性，要求卷積碼序列長度N≥3（L+1）。由于L也是未知的，所以要設(shè)置一個較大的估計值，通常是實際約束長度的數(shù)倍，而且未知參數(shù)L與N是相同數(shù)量級，所以必須采集足夠長的數(shù)據(jù)。同時方程組（2）的可解性還與信源有關(guān)，方程組（2）有惟一解的概率只有50％［4］。

第三，當(dāng)卷積碼的總約束長度較大時，識別過程非常耗時，因此無法在實際中應(yīng)用。

因此，采用常規(guī)識別算，如何提高識別效率是重中之重。

3.2 基于校驗矩陣的識別算法

卷積碼序列G與校驗矩陣H存在如下校驗關(guān)系［5］

校驗矩陣多項式的最高階數(shù)根據(jù)實際應(yīng)用設(shè)定為k，卷積碼輸出路數(shù)n，容易得到校驗矩陣多項式系數(shù)的齊次線性方程組

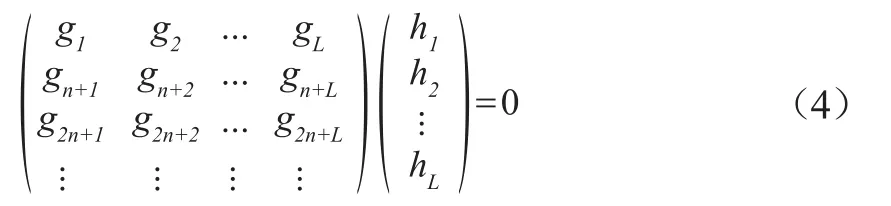
式中，gi為接收序列中第i位；L=n（k+1）。文獻(xiàn)［6］針對式中的模型給出了相應(yīng)的求解算法，將1/2碼率卷積碼校驗矩陣的求解模型轉(zhuǎn)化為關(guān)鍵模方程表示［7］，求解該算法即轉(zhuǎn)化為在集合φ（n）中尋找元素（h1（x）,h2（x）,k），使得k達(dá)到最小且（h1（0）,h2（0））≠（0,0），φ（n）的定義如下

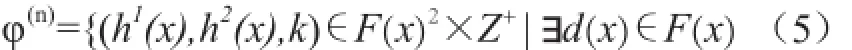
其中，F(xiàn)（x）為二元域上的多項式環(huán)。

3.3 基于歐幾里德算法的識別算法

歐幾里德算法又稱輾轉(zhuǎn)相除法［5］，是一個迭代算法，可以用于計算兩個多項式a（x）和b（x）的最大公約數(shù)d（x），然后找到一個表示a（x）和b（x）之間的線性聯(lián)系，使其等于d（x），即找到方程

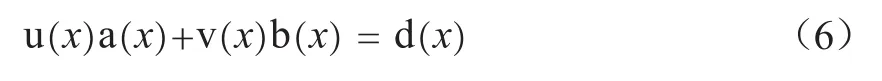
本方法即是應(yīng)用歐幾里得算法在有限域上的算法來求解卷積碼生成多項式的。對于一個1/2碼率的卷積碼的識別，接收到的碼字多項式是已知的c1（x）和c2（x），目標(biāo)是尋找多項式g1（x）和g2（x），使得

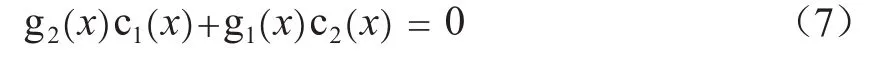
由于接收到的數(shù)據(jù)只是卷積碼編碼數(shù)據(jù)的一部分，并且，編碼序列在傳輸過程中，也會遭受噪聲的影響，使得c1（x）和c2（x）不一定滿足式（7），所以需要對歐幾里德算法進(jìn)行修正，修正后的歐幾里德算法過程如下：

第一步：參數(shù)初始化

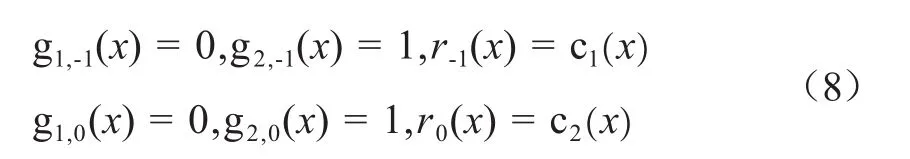
第二步：對于i≥1，定義qi（x），ri（x）滿足ri-2（x）= qi（x）ri-1（x）+ri（x），其中qi（x），ri（x）分別是ri-2（x）除以ri-1（x）所得到的商多項式和余數(shù)多項式。

第三步：迭代運算

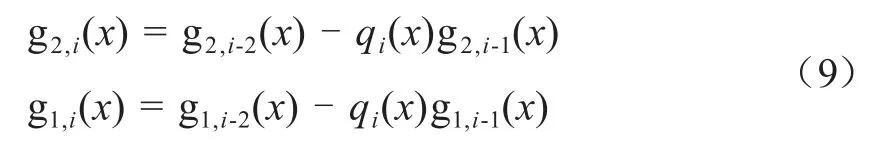
第四步：終止條件

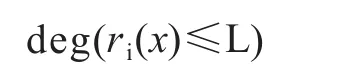
設(shè)此時i=n，可以得到g1（x）=g1,n（x）,g2（x）= g2,n（x）。

4 算法性能比較

4.1 正確識別率比較

根據(jù)相關(guān)文獻(xiàn)資料［8］可以得到前述三種算法在識別完全無誤卷積碼時的正確識別率，如表1所示。由表1可以看出，除了常規(guī)算法以外，另二種識別算法都能正確識別接收到的完全無誤卷積碼，正確識別率可以達(dá)到 。

表1　正確識別率比較結(jié)果

4.2 抗誤碼性比較

表2列出了3種算法的抗誤碼性能［4］，從表中可以看出，除了常規(guī)算法以外，另外兩種識別算法都具有一定的抗誤碼能力，基于校驗矩陣的匹配識別算法抗誤碼能力與誤碼發(fā)生在截取碼流中的位置有關(guān)；基于歐幾里德算法的識別算法只能抗少量誤碼。

表2　抗誤碼性能比較結(jié)果

4.3 計算復(fù)雜度比較

常規(guī)識別算法的計算復(fù)雜度是O（N3）（其中N是接收碼字長度）、基于校驗矩陣的匹配識別算法的計算復(fù)雜度隨著接收碼字長度N的增加而增加，基于歐幾里德算法最多需要L×N/2次多項式乘法和加法運算，其中L是生成多項式g1（x），g2（x）的最大階次，即L=max（degg1（x）,degg2（x））；N是用于求解的碼字序列長度，N≥3（L+1）。在接收碼長N一定時，常規(guī)識別算法的計算復(fù)雜度最高，基于歐幾里德算法的計算復(fù)雜度最低。

4.4 綜合比較

綜合上文對三種識別算法在識別1/2碼率卷積碼時的性能比較可以發(fā)現(xiàn)，常規(guī)識別算法無論在正確識別率、抗誤碼性能還是在計算復(fù)雜度上都不及其他算法；基于校驗矩陣的匹配識別算法計算最簡便，但抗誤碼性能不穩(wěn)定，而基于歐幾里德算法的識別算法正確識別率高、計算復(fù)雜度低，但是其抗誤碼性能有待改進(jìn)。

5 總結(jié)與展望

隨著通信對抗逐漸從信號對抗轉(zhuǎn)向信息對抗，信道編碼盲識別技術(shù)的地位越來越重要。本文簡要介紹了現(xiàn)有三種卷積碼信道編碼的盲識別方法，分析了三種識別算法的算法性能。從分析中可以看到，現(xiàn)有信道編碼識別技術(shù)尚存在許多局限和不足，需要進(jìn)一步研究來補充和完善：在識別對象上，現(xiàn)有的研究主要集中在卷積碼的研究，其他信道編碼體制，如BCH碼、RS碼、Turbo碼以及LDPC等的相關(guān)研究資料非常少；目前的卷積碼識別方法也存在很多不足，普通卷積碼的識別方法僅對1/2碼率有效，不能適應(yīng)高碼率的情況，刪除卷積碼的識別方法不能快速穩(wěn)定地完成識別，等等。■

參考文獻(xiàn)

［1］ 杜宇峰.信道編碼分析識別技術(shù)研究［D］.西安：電子科技大學(xué)，2012

［2］ 劉健，謝锘，周希元.RS碼的盲識別方法［J］.電子科技大學(xué)學(xué)報，2009,38（3）：363-368

［3］ 解輝，王豐華，黃知濤.基于改進(jìn)歐幾里得算法的1/2碼率卷積碼盲識別方法［J］.電子對抗，2010,1：32-36

［4］ 宋鏡業(yè).信道編碼識別技術(shù)研究［D］.西安：西安電子科技大學(xué)，2009

［5］ J H van Lint. Introduction to Coding Theory［M］.Beijing：World Publishing Corporation,2003.

［6］ 周亞建，劉健.（n,n-1,m）卷積碼的盲識別［J］.北京郵電大學(xué)學(xué)報，2010,33（3）：135-138

［7］ 鄒艷，陸佩忠.關(guān)鍵方程的新推廣［J］.計算機學(xué)報，2006,29（5）：711-718

Analysis of the Recognition Algorithm of Convolutional Code

Ding Qiao1, Xu Wei2
（1.PLA University of Science and Technology, Nanjing, 210007； 2.Air Force Communication Network Management Center, Beijing, 100843）

Abstract:Overview of the development of the recognition of channel coding technology is presented in this paper, the working principle of three convolutional code recognition algorithms, i.e.conventional recognition algorithm, parity check matrix-based recognition algorithm and Euclidean-based recognition algorithm is given, comparative analysis of three algorithms’-performance is presented in this paper.

Keywords:Convolutional encoding； Coding Recognition； Parity check matrix； Euclidean algorithm；Algorithm performance

doi：10.3969/J.ISSN.1672-7274.2016.06.004

中圖分類號：TN97，TN92

文獻(xiàn)標(biāo)識碼：A 文章編碼：1672-7274（2016）06-0011-03

作者簡介：丁 嶠，解放軍理工大學(xué)通信工程學(xué)院通信工程專業(yè)學(xué)生。