“控制工程基礎”課程中梅遜增益公式的應用技巧
宋 強,師會超
(安陽工學院機械工程學院,河南安陽455000)
?
“控制工程基礎”課程中梅遜增益公式的應用技巧
宋 強,師會超
(安陽工學院機械工程學院,河南安陽455000)
摘要:提出了通過計算機檢索和分叉法來確定梅遜增益公式的回路和前向通道傳遞函數,確定特征余因子,利用梅遜公式求解系統閉環傳遞函數,為正確運用梅遜增益應用奠定了基礎。
關鍵詞:梅遜公式;計算機檢索;分叉法;傳遞函數
0引言
在“控制工程基礎”課程教學中,很多同學感覺這門課程概念多、公式多、應用多,糅合物理化學加之數學,學起來很難理解,剛開始學生信誓旦旦一定要學好,但隨著課程地不斷深入,學生有點吃不消了,感覺此門課“難于上青天”,隨之第二章第三章呼嘯而來,大多同學乖乖舉手投降、上課時在呼呼黃粱美夢中度過十分珍貴的時間!為此,為了學好這門課程,我們來列舉一些學習技巧以供參考。控制工程基礎課程我們只講單輸入單輸出的經典控制理論,簡單的單回路控制同學們還能理解,對于復雜的控制系統,大多同學感覺云里霧里迷茫一片。解決復雜控制系統一般由方框圖化簡法或采用梅遜增益公式求解,采用方框圖化簡一般要移動求和點或引出點,對于互相交叉且回路眾多的復雜系統來說,方框圖化簡也很難湊效,這種系統我們只好求助于梅遜增益公式,梅遜增益公式的學習有些技巧,下面就計算機檢索法和分叉法進行介紹。
1 梅遜公式的應用
當系統信號流圖已知時,可以用公式直接求出系統的傳遞函數,這個公式就是梅遜公式。由于信號流圖和結構圖存在著相應的關系,因此梅遜公式同樣也適用于結構圖。
梅遜公式給出了系統信號流圖中,任意輸入節點與輸出節點之間的增益,即傳遞函數。其公式為

式中n——從輸入節點到輸出節點的前向通路的總條數。
Pk——從輸入節點到輸出節點的第k條前向通路總增益。
Δ——為特征式,由系統信號流圖中各回路增益確定:
Δ=1-∑La+∑LbLc-∑LdLeLf+…
式中 ∑La——所有單獨回路增益之和;
∑LbLc——所有存在的兩個互不接觸的單獨回路增益乘積之和;
∑LdLeLf——所有存在的三個互不接觸的單獨回路增益乘積之和;
Δk——為第k條前向通路特征式的余因子式,即在信號流圖中,除去與第k條前向通路接觸的回路后的Δ值的剩余部分。
上述公式中的接觸回路是指具有共同節點的回路,反之稱為不接觸回路。與第k條前向通路具有共同節點的回路稱為與第k條前向通路接觸的回路。由梅遜公式可以看出,總增益P實際上就是系統某兩點之間的傳遞函數,特征式Δ實際上就是閉環系統的特征多項式。
根據梅遜公式計算系統的傳遞函數,首要問題是正確識別所有的回路并區分它們是否相互接觸,正確識別所規定的輸入與輸出節點之間的所有前向通路及與其相接觸的回路。
采用這種方法,要注意以下過程:
1)要搞清回環的個數,定要數清單回路的個數;搞不清回路的個數,第一步就計算錯了,這是梅遜增益公式應用的基礎。
2)要注意互不接觸回路的個數,一般三個不接觸回路基本不存在,我們一般使用“計算機檢索”的方法來決定互不接觸回路的個數,所謂計算機檢索的方法,將加入控制系統有n個互不相同的回路,定義為Ln(n=1,2,3,…,n),從L1回路開始依次和L2、L3、…,Ln看能否構成兩個互不接觸回路,如果兩個回路沒有公共節點就構成兩個互不接觸回路,L1檢索結束再從回路L2回路開始檢索,L2結束再從L3開始,直至檢索到Ln結束。這樣重復的檢索次數為
,按照此方法不會漏掉一個兩個互不接觸回路。也可以按照計算每兩個互不接觸回路傳遞函數乘積,如果發現計算的傳遞函數有某個傳遞函數的平方,那一定計算錯了。仔細檢查就可以確定那部分錯了。
3)對于第k條前向通道特征余因子的確定技巧。定義Δk為第k條前向通路特征式的余因子式,即在信號流圖中,除去與第k條前向通路接觸的回路后的Δ值的剩余部分。里面包含兩層意思;第一,特征余因子Δk是和第k條前向通道相對應的,也就是與第一條前向通道P1對應的特征余因子是Δ1,與第二條前向通道P2對應的特征余因子是Δ2,與第k條前向通道P1對應的特征余因子是Δk,也就是說特征余因子是相對于某條前向通道而言的,前向通道變化了其對應的特征余因子也會變化。第二,Δk的求取方法:對于前向通道P2的相對應的Δ2,與前向通道P2相接觸的回路代以零值,不接觸的回路保留原值,這樣就可以確定Δ2,對于三個不接觸回路也是在Δ的基礎之上求取的。
4)分叉法從信號流圖中輸入節點開始,作為分叉法的第一層。只考慮從此節點流出的箭頭而不考慮流入的箭頭,到達下一個節點作為第二層。同理依照箭頭方向依次向下傳遞作為第i+1層,直至到達輸出節點。輸入節點級別最高,輸出節點級別最低。
下面列舉一些例子來闡述
例1試求如圖1所示系統的傳遞函數。
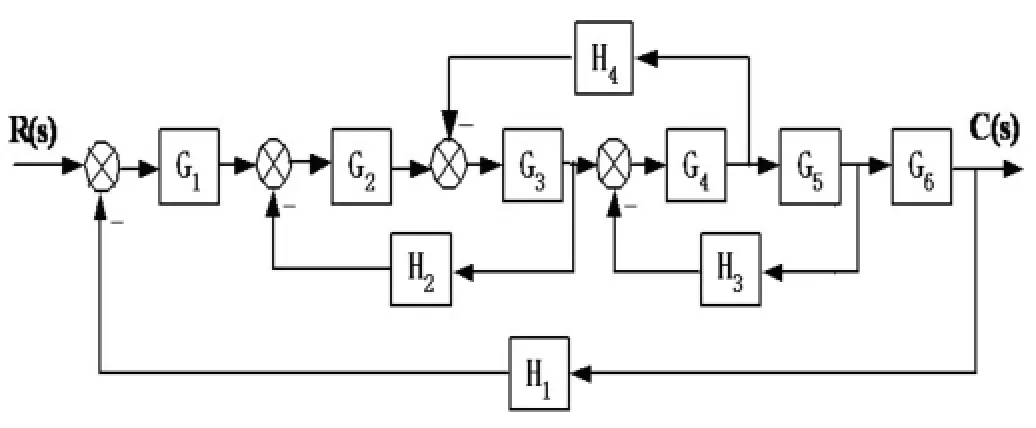
圖1 系統結構圖
解:步驟1:找出前向通路數n
前向通路數:n=1,P1=G1G2G3G4G5G6
步驟2:確定系統中的反饋回路及其增益
L1=-G1G2G3G4G5G6H1,L2=-G2G3H2,L3=-G4G5H3,L4=-G3G4H4
步驟3:利用梅遜公式求傳遞函數

使用計算機檢索方法,L2l3兩兩互不接觸
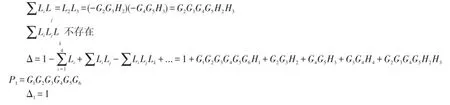

例2用梅遜公式求如圖2所示系統的傳遞函數。

圖2 系統的方框圖
解:步驟1:確定反饋回路L1=-G1G2G3,L2=-G1G2H1,L3=-G2G3H2,L4=-G1G4
L5=-G4H2
步驟2:確定前向通路P1=G1G2G3,Δ1=1,P2=G1G4,Δ2=1
步驟3:求總傳遞函數

3 結論
本文針對梅遜公式的應用提出了計算機搜索和分叉法等方法和應用技巧,這些為準確理解、靈活運用梅遜公式及其應用奠定了基礎,是值得研究和思索的。
參考文獻:
[1]宋強.機械工程控制基礎[M].北京:中國鐵道出版社,2014.
(責任編輯:郝安林)
Mason Gain Formula Application Skills
SONG Qiang,SHI Huichao
(School of Mechanical Engineering Anyang Institute of Techonogy,Anyang 455000,China)
Abstract:This paper presents a computer retrieval and bifurcation method to determine the mason gain formula of circuit and the forward channel transfer function,also determine the characteristics of more factors,using ma?son formula to solve the system closed loop transfer function,laid the foundation for the correct use mason gain application.In this article,through specific examples.
Key words:Mason formula;computer retrieval;bifurcation method;the transfer function
中圖分類號:G420
文獻標志碼:A
文章編號:1673-2928(2016)02-0119-03
收稿日期:2015-01-03
作者簡介:宋強(1972-),男,安陽工學院機械工程學院副教授,研究方向:智能控制、過程控制、計算機及其應用。

