寬頻激勵下雙穩態壓電振動發電機供電能力分析

何青，　毛新華,2，　褚東亮

(1.華北電力大學 電站設備狀態監測與控制教育部重點實驗室，北京 102206；2.北京中麗制機工程技術有限公司，北京 101111)

?

寬頻激勵下雙穩態壓電振動發電機供電能力分析

何青1，毛新華1,2，褚東亮1

(1.華北電力大學 電站設備狀態監測與控制教育部重點實驗室，北京 102206；2.北京中麗制機工程技術有限公司，北京 101111)

摘要:為了探討雙穩態壓電振動發電機在寬頻激勵下的供電能力問題，建立了寬頻激勵下雙穩態壓電振動發電機系統的動力學模型，仿真了雙穩態壓電振動發電機系統的輸出響應特性和不同運動狀態的輸出電壓特性，研究了雙穩態壓電振動發電機系統運行在高能量軌道上的激勵條件，據此優化雙穩態壓電振動發電機結構參數，并對傳感器網絡節點的用電需求和雙穩態壓電振動發電機的供電能力進行分析。仿真和實驗結果表明：雙穩態壓電振動發電機在寬頻激勵下，其輸出平均功率為3.8 mW，能夠滿足實際振動環境下無線傳感器網絡節點的用電需求。

關鍵詞:振動；寬頻；能量收集；發電機；雙穩態；動態響應

0引言

振動能量廣泛存在于橋梁、汽車、輸電導線、電廠旋轉設備等各種環境中，利用振動能量采集技術將環境中的振動能量轉換為電能，不僅可以為無線傳感器網絡節點等低功耗的電子設備供電，還可以減小振動對周圍環境中結構的損傷和破壞[1-4]。但真實環境中振動的寬頻特性與隨機性使得傳統壓電振動發電機供電具有很大的局限性，當傳統壓電振動發電的頻率與環境激勵頻率相差5%時，壓電振動發電機幾乎收集不到任何能量。雙穩態壓電振動發電機利用自身結構提供的非線性力，在寬頻激勵下的發電機系統產生跳躍現象，能極大拓展壓電振動發電機的諧振帶寬，提高寬頻激勵環境下的輸出功率[5-6]。

目前，雙穩態壓電振動發電機因具有較寬的諧振帶寬特性而成了振動能量收集領域的研究熱點[7-8]。文獻[9]利用一對磁鐵為壓電振動發電機提供非線性力，實現了寬頻激勵下的輸出大幅響應，提高了壓電振動發電機的諧振帶寬；但只做了實驗研究，沒有對壓電振動發電機運動的機理與本質特性進行分析。文獻[10]建立了雙穩態壓電振動發電機系統的數學模型，分析了雙穩態共振發生的頻率條件和不同頻率激勵下的輸出功率；但只考慮了弱周期激勵下的頻率變化情況，沒有考慮激勵幅值變化對輸出電壓的影響。文獻[11]和[12]建立了磁力模型和壓電懸臂梁發電機系統的集總參數模型,仿真了壓電振動發電機的動態響應特性，并分析了頻率變化和幅值變化對輸出特性的影響；但文獻中建立的集總參數模型有較大的模型誤差，這對于輸出功率原本不高的壓電振動發電機在定量分析供電能力時所帶來的誤差將會更大。文獻[13]研究了不同激勵下雙穩態振動發電機系統的非線性振動特性，從理論角度對壓電振動發電機系統的幅值跳躍、多解現象進行了釋疑；但未考慮激勵的幅值閾值對輸出特性的影響。振源的頻率變化和幅值變化相互交織影響著雙穩態壓電振動發電機的輸出特性和供電能力；而上述這些研究涉及這些方面的分析較少，尤其是針對實際寬頻激勵環境下的供電能力分析更少[14-16]。

本文建立了帶有修正參數的雙穩態壓電振動發電機的集總參數模型，通過數值方法仿真了壓電振動發電機的輸出特性和不同運動狀態下的輸出電壓特性，研究了雙穩態壓電振動發電機在高能量軌道上運行的激勵條件，并優化了壓電振動發電機的結構參數，分析了雙穩態壓電振動發電機在寬頻激勵下的供電能力，為雙穩態壓電振動發電機的設計與實際應用提供了理論指導。

1雙穩態壓電振動發電機的動力學模型

雙穩態壓電振動發電機的結構類型很多，其中，懸臂梁式雙穩態壓電振動發電機以結構簡單、體積小、成本低、易于微型化等優點成為壓電振動發電機主流結構，其結構如圖1所示。該結構由支架A、金屬懸臂梁B、壓電陶瓷片P(PZT)、外部磁鐵C和D組成。PZT壓電陶瓷片粘貼在懸臂梁的根部，壓電陶瓷片上引出的兩個電極與外接負載電阻RL相連接。懸臂梁的長度、寬度、厚度分別表示為L、b、h,壓電片的長度、寬度、厚度分別表示為Lp、bp、hp，磁鐵C和磁鐵D的間距為d，懸臂梁固定端到磁鐵中心的距離為l，懸臂梁的質量為mb，壓電片的質量為mp，外部磁鐵質量均為mc。在振源的激勵下，懸臂梁產生諧振而引起PZT壓電陶瓷形變，依據壓電效應而在壓電陶瓷的兩端產生電壓，可將環境的振動能轉換為電能。當兩個磁鐵的間距在合適位置時，懸臂梁式壓電振動發電機表現為雙穩態特性。

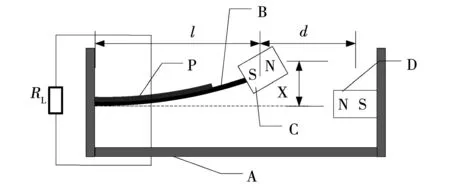
圖1　雙穩態壓電振動發電機結構圖Fig.1　Bistable piezoelectric vibration generator　　　 diagram

懸臂梁式壓電振動發電機的運動形式主要是以一階模態為主，其動力學模型可簡化為集總參數模型；但集總參數模型帶來的誤差較大，故引入修正參數κ1，以平衡模型誤差。根據雙穩態壓電振動發電機結構的受力分析和牛頓第二定律，雙穩態壓電振動發電機系統的力學方程[17-20]為

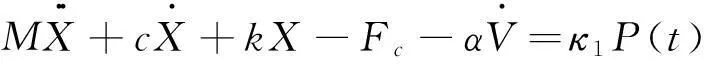
(1)

其中：X為懸臂梁末端磁鐵的振動位移；V為壓電陶瓷片兩端產生的電壓；M,c,k為壓電懸臂梁的等效質量、等效阻尼和等效剛度；Fc為磁力在振動方向上的分量；α為機電耦合系數；κ1為集總參數模型的修正系數；P(t)=MAsin(Ωt)假設為正弦激勵，t為時間。等效質量M、等效阻尼k、等效剛度c、磁力分量Fc、機電耦合系數α和集總參數模型的修正系數κ1分別由下列方程計算給出。

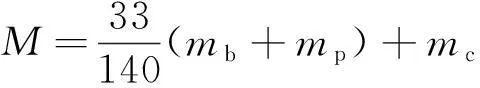
(2)

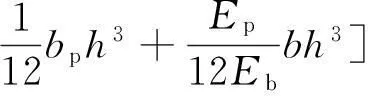
(3)

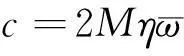
(4)

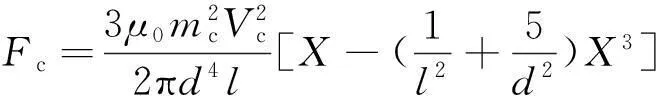
(5)

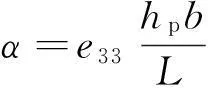
(6)

(7)

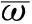
根據基爾霍夫電流定律，雙穩態壓電振動發電機的電學方程如下：

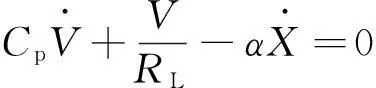
(8)

其中Cp為壓電陶瓷的等效電容，其計算公式為

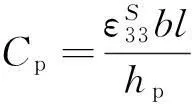
(9)

將式(2)～式(7)分別代入式(1)，式(9)代入式(8)中，對代入結果進行無量綱化處理，則新的動力學方程可變為：

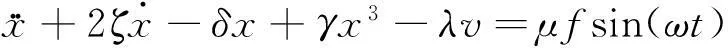
(10)

(11)

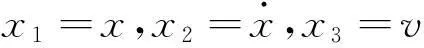
(12)

2輸出性能仿真分析與結構優化

2.1輸出響應特性仿真分析

仿真所需參數取值為：η=0.02，e31=-5.35 N/mV，雙穩態壓電振動發電機結構的參數如表1所示。為獲得寬頻激勵下雙穩態壓電振動發電機的輸出響應特性，分別以激勵的頻率變化和幅值變化為變量，采用數值方法求解狀態方程式(12)，得到頻率變化、幅值變化時的分岔圖。

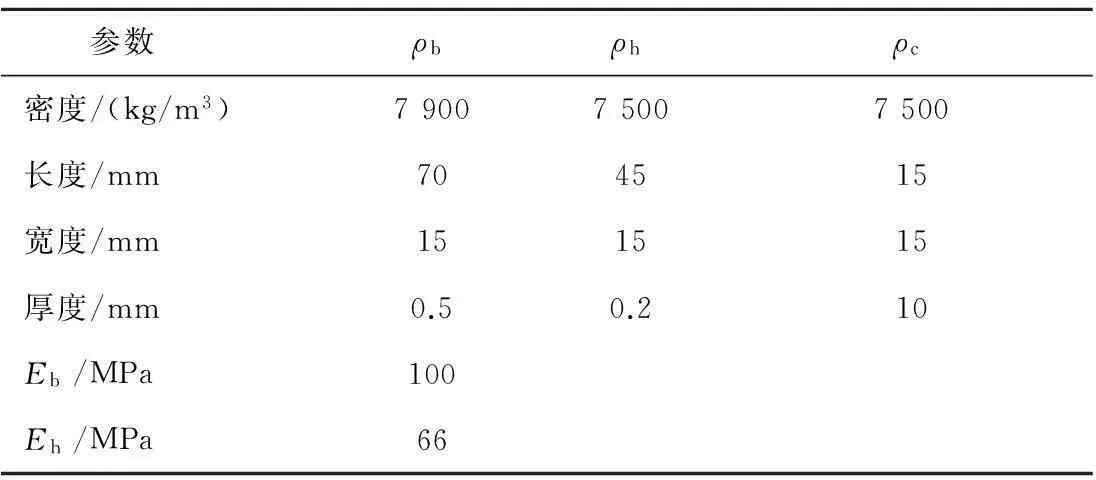
表1　壓電振動發電機參數

當無量綱激勵幅值大于等于0.409時，系統能夠產生大幅周期運動，如圖2(b)～(d)，且從單個頻率分岔圖看，隨著激勵頻率的增加，系統先后經歷單阱內小幅周期運動、雙阱間大幅周期運動、倍周期運動、雙阱間大幅混沌運動，最后又回到單阱內做小幅運動。產生這種現象的原因是當激勵頻率較低時，系統獲得的能量也較低，不足以跨越系統的幅值閾值，而只能在某一勢阱內做小幅運動，此時雙穩態壓電振動發電機在低能量軌道上運行。隨著激勵頻率的增大，系統獲得足夠的能量越過幅值閾值而產生大幅運動，此時雙穩態壓電振動發電機在高能量軌道上運行。而當無量綱激勵幅值小于0.409時，如圖2(a)，系統不能產生大幅周期運動，從單個激勵頻率分岔圖看，系統在經歷單阱內小幅周期運動后直接進入倍周期運動，然后進入混沌運動和單阱小幅運動。

分析圖2可知，不論激勵幅值大小如何，隨著激勵頻率的增加，系統最終都又回到單阱內做小幅周期運動，這是因為激勵頻率增大的同時，系統的幅值閾值也在增加，當激勵頻率增大到一定值時，系統此時的能量又將低于新的幅值閾值，雙穩態壓電振動發電機又只能在勢阱內做小幅運動。這表明系統發生大幅響應運動不僅有下限的激勵頻率閾值，而且還有上限激勵頻率閾值。

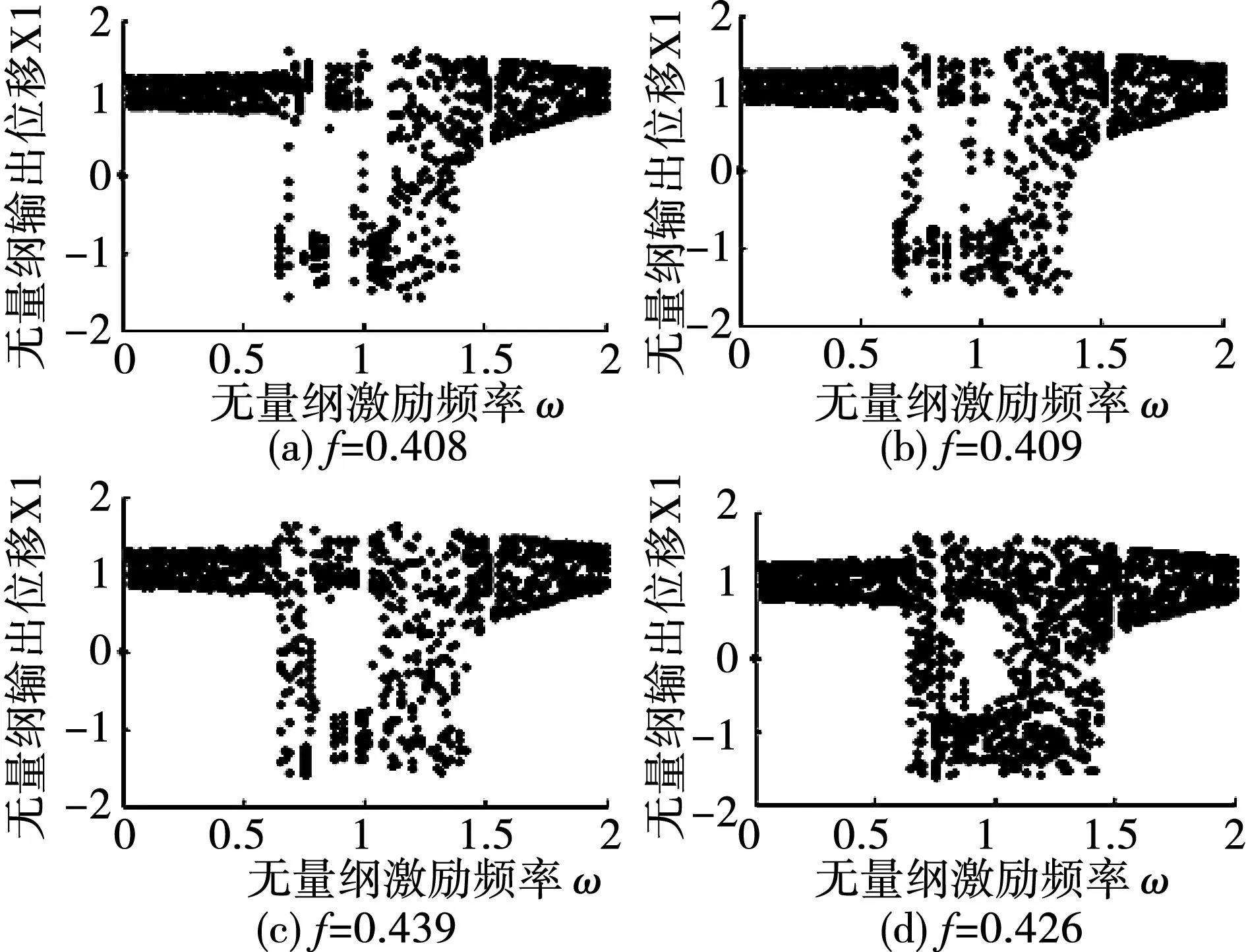
圖2　激勵頻率分岔圖Fig.2　Excitation frequency bifurcation diagram

分析如圖3所示的單個激勵幅值的分岔圖可知，當無量綱激勵幅值大于幅值閾值時，系統在勢阱間發生大幅響應運動，且隨著激勵幅值增加，系統一直保持大幅輸出響應運動。這表明雙穩態振動發電機系統只有下限激勵幅值閾值沒有上限激勵幅值閾值。比較圖3(a)與圖3(b)可知，激勵頻率越低時，系統發生大幅運動所需要的激勵幅值也越小。

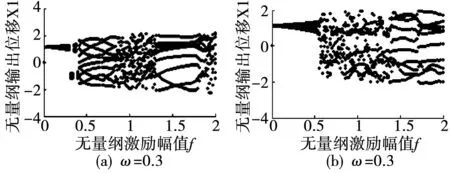
圖3　激勵振幅分岔圖Fig.3　Excitation amplitude bifurcation diagram

2.2不同運動狀態的電壓輸出特性

圖4為無量綱激勵幅值等于0.409時，壓電振動發電機不同運動狀態下的輸出電壓特性。分析圖4可知：小幅周期運動和倍周期運動的輸出電壓都比較低，其峰值電壓低于3 V，無法給無線傳感器節點供電。大幅周期運動和混沌運動的輸出電壓較大，其峰值電壓大于3 V，可以為無線傳感器節點供電。根據式(13)，計算得到大幅周期運動狀態下輸出電壓的有效值為8.7 V，混沌運動狀態下輸出電壓的有效值為4.3 V。這說明，大幅周期運動狀態的供電能力高于混沌狀態下的供電能力。

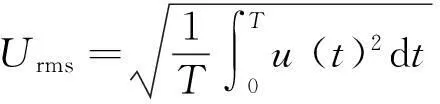
(13)

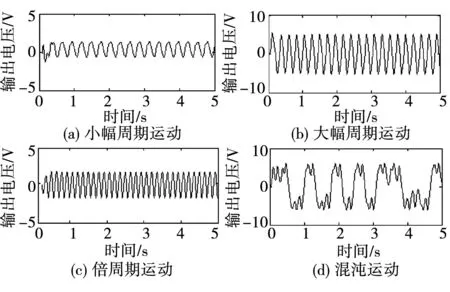
圖4　f=0.409時，不同運動狀態的輸出電壓Fig.4　System output voltage of the different　　　 behavior when f=0.409

3.3結構參數對激勵幅值閾值的影響分析

雙穩態壓電振動發電機的勢能方程可表述為式(14)所示，根據文獻[21]的研究結果，振源激勵的幅值閾值Ac與振源頻率ω之間的關系如式(15)所示。

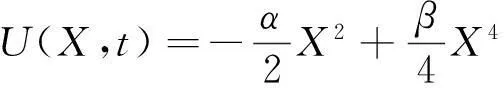
(14)

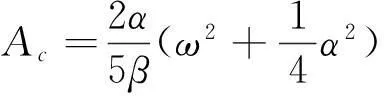
(15)

激勵幅值分岔圖仿真結果表明，只有當激勵幅值大于系統要求的最低激勵幅值(幅值閾值)時，雙穩態壓電振動發電機才能獲得大幅輸出響應。由式(15)知，系統結構參數恒定時，不同激勵頻率有著不同的幅值閾值，且幅值閾值隨著激勵頻率的增大而增大；而在實際的振動環境下，頻率較高時振幅一般往往較低，這使壓電振動發電機諧振帶寬變小，降低了寬頻振動能量收集效率。

優化雙穩態壓電振動發電機結構參數，降低系統的幅值閾值，進一步擴大雙穩態壓電振動發電機的諧振帶寬，可提高寬頻振動能量收集效率。圖5為不同結構參數的雙穩態壓電振動發電機所對應的幅值閾值隨頻率變化的關系。該圖表明，懸臂梁的長度和剛度對激勵幅值的閾值影響較大，長度越長或者剛度越小，發生大幅響應運動所需要的幅值閾值越低，越有利于收集低幅值的寬頻振動能量，而懸臂梁的寬度和厚度對幅值閾值的影響較小。

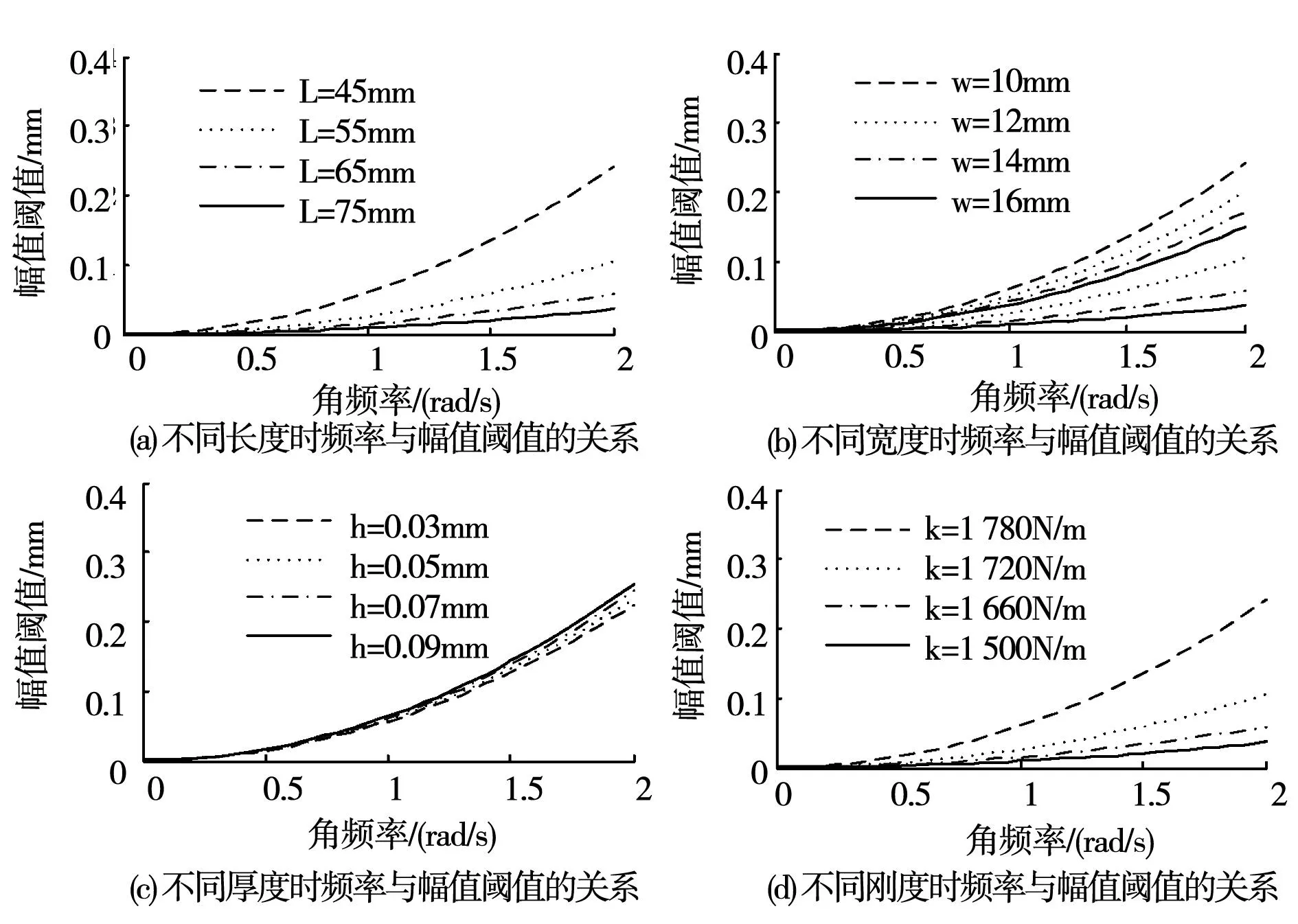
圖5　結構參數對幅值閾值的影響Fig.5　Influence of structure parameters on　　　 the amplitude threshold

3實驗測試及供電能力分析

3.1實驗測試驗證

為驗證仿真結果，構建了如圖6所示的壓電振動發電機實驗測試系統。測試系統由SPF05函數信號發生器、GF-10型功率放大器、ZJY-601激振臺、BVM-200測振表、加速度傳感器、數據采集卡、DS1102C數字存儲示波器等儀器和設備組成。實驗原理為：SPF05函數信號發生器產生寬頻信號，經GF-10功率放大器的輸出到ZJY-601激振臺進行振動控制，調節信號頻率和功率放大器的輸出振幅，用振動計測得激振臺的頻率和振幅，以模擬寬頻激振環境。將能量采集器固定在激振器上，觀察并記錄示波器輸出電壓波形與數值，并計算出不同負載時的輸出功率。實驗結果如圖8、圖9所示。

圖8為激勵幅值變化時，雙穩態壓電振動發電機輸出電壓變化規律。結果表明：雙穩態壓電振動發電機系統存在幅值閾值，只有當激勵幅值大于幅值閾值時，系統才能發生大幅響應，才能在高能量軌道上運行，輸出電壓才較大。而且激勵頻率越大，幅值閾值也越大，同時幅值閾值只有下限沒有上限，這與3.1仿真結果相一致。

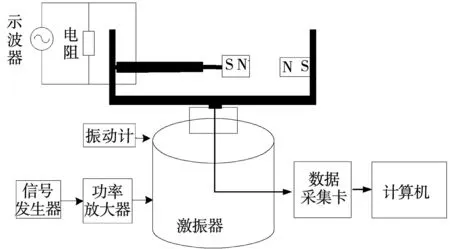
圖6　實驗平臺Fig.6　Experimental platform

圖7　實驗裝置與樣機Fig.7　Experimental facility and prototype

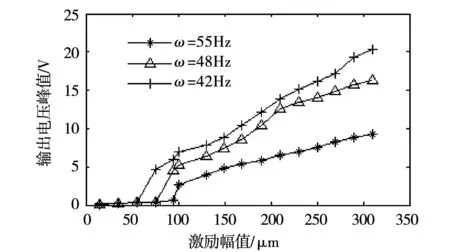
圖8　不同激勵時系統的輸出電壓Fig.8　System output voltage under different　　　excitation

圖9(a)為激勵頻率變化時雙穩態壓電振動發電機輸出電壓變化規律。結果表明：當激勵頻率在33～55 Hz時，壓電振動發電機的輸出端的峰值電壓大于3 V，而在其余頻段壓電振動發電機幾乎沒有電壓輸出。這表明雙穩態壓電振動發電機系統存在頻率閾值，而且該頻率閾值既有下限值也有上限值。根據圖9(a)的實驗數據和式(13)、式(16)，可求得不同負載值的輸出功率，如圖9(b)所示。分析圖9(b)可知，雙穩態壓電振動發電機的輸出功率與負載大小相關，負載越大，輸出平均功率越低。當激勵頻率在33～55 Hz范圍內、負載為150 kΩ時，可計算出雙穩態壓電振動發電機在該頻段內的平均輸出功率約為3.8 mW。

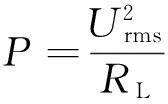
(16)

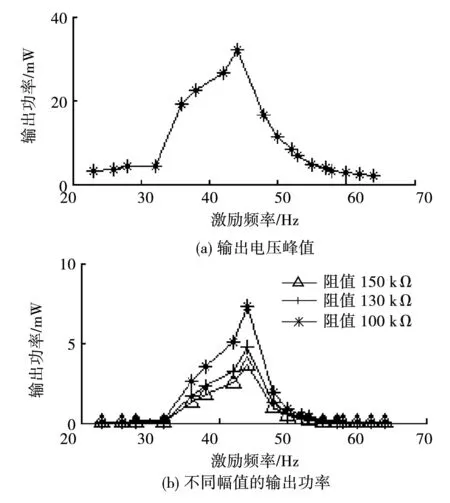
圖9　雙穩態壓電振動發電機的輸出電壓和功率Fig.9　Output voltage and power of bistable　　　piezoelectric vibration generator

3.2供電能力分析

壓電振動發電機輸出的電壓是交流電壓，為了給低功耗的傳感器節點提供穩定的電能，常采用能量收集電路模塊LTC3588-1對壓電振動發電機輸出的電壓進行整流、濾波、模數轉換等調理，輸出的穩定電能再由超級電容儲存，以備供傳感器節點使用。

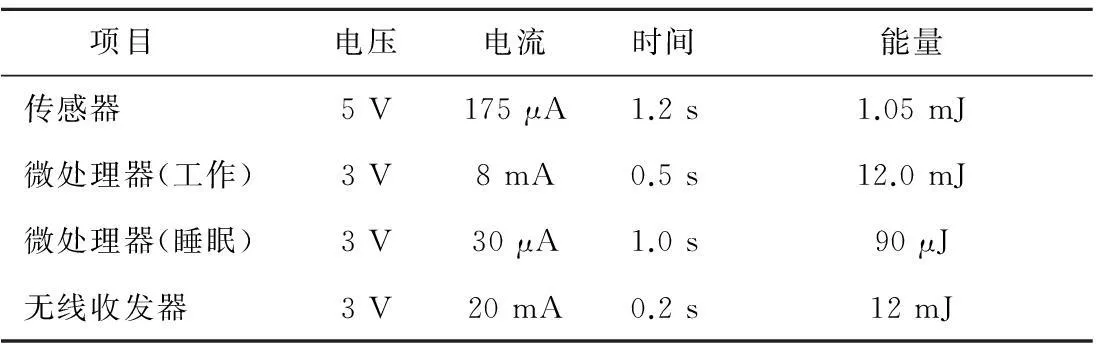
表2　傳感器節點電路能量消耗情況

應用于監測系統的傳感器網絡節點系統主要包括加速度傳感器、微處理器、射頻無線收發器等器件，各器件的平均耗能情況[22-23]如表2所示。根據表2，傳感器網絡節點串聯負載約為130 kΩ,發射一次信息需要的功耗為20 mJ。如果監測系統間隔1分鐘采集發射一次信息，雙穩態壓電振動發電機1分鐘內收集到的能量平均約為228 mJ，能夠滿足傳感器網絡節點的用電需求。

4結論

1)外界的激勵條件決定著雙穩態壓電振動發電機的輸出特性，只有當外界激勵大于系統的頻率閾值和幅值閾值時，雙穩態壓電振動發電機才能發生大幅響應運動，雙穩態壓電振動發電機才能在高能量軌道上運行。

2)雙穩態壓電振動發電機的結構參數與系統閾值的大小密切相關。對于懸臂梁式的壓電振動發電機，增大懸臂梁的長度或者降低壓電振動發電機的剛度，能夠有效降低系統的幅值閾值，有利于收集寬頻、低幅的振動能量。

3)雙穩態壓電振動發電機具有較大的諧振帶寬和較高輸出功率，能夠滿足傳感器網絡節點用電需求，解決了實際振動環境下傳感器網絡節點供電問題。

參 考 文 獻:

[1]陳仁文．新型環境能量采集技術[M]．北京：國防工業出版社，2011:1-10．

[2]邱清泉, 肖立業, 辛守喬,等. 微型振動式壓電發電機的設計與特性分析[J]. 電機與控制學報, 2011, 15(7):1-7.

QIU Qingquan,XIAO Liye，XIN Shouqiao，et al. Design and performance analysis for micro piezoelectric vibration generator [J]. Electric Machines and Control, 2011, 15(7):1-7.

[3]何青，毛新華，褚東亮．隨機激勵下雙穩態壓電振動發電機的振動特性[J]．噪聲與振動控制，2015,35(2)：36-40．

HE Qing, MAO Xinhua, CHU Dongliang. Dynamic characteristics of a bistable piezoelectric vibration generator under random excitation [J]. Noise and Vibration Control, 2015,35(2):36-40．

[4]賓洋,楊東超，陳娜娜，等. 新型壓電驅動機電耦合動力學系統分析與建模[J]. 電機與控制學報, 2008, 12(2):179-183.

BIN Yang, YANG Dongchao, CHEN Nana, et al. Analysis and modeling of a novel piezo-actuated electromechanical coupling dynamic system[J]. Electric Machines and Control, 2008, 12(2): 179-183.

[5]閆震,何青. 激勵環境下懸臂梁式壓電振動發電機性能分析[J]. 中國電機工程學報,2011,31(30): 140-145．

YAN Zhen, HE Qing. Performance analysis on incentive environment of micro cantilever piezoelectric vibration generator [J]. Proceedings of the CSEE, 2011, 31(30): 140-145.

[6]劉祥建,陳仁文. 壓電振動能量收集裝置研究現狀及發展趨勢[J]. 振動與沖擊,2012,31(16): 169-175.

LIU Xiangjian，CHEN Renwen．Current situation and developing trend of piezoelectric vibration energy harvesters[J]．Journal of Vibration and Shock，2012,31(16):169-175.

[7]袁江波，謝濤，單小彪，等．復合型懸臂梁壓電振子振動模型及發電試驗研究[J]．機械工程學報，2010，46(9)：87-92.

YUAN Jiangbo，XIE Tao，SHAN Xiaobiao， et al．Vibrated model and experiments of multiple piezoelectric cantilevers in energy harvesting [J]. Journal of Mechanical Engineering，2010，46(9)： 87-92.

[8]HAME R L,WANG K W.A review of the recent research on vibration energy harvesting via bistable systems [J]. Smart Materials & Structures，2013,(22):1-12．

[9]TANG L, YANG Y, SOH C K. Improving functionality of vibration energy harvesters using magnets [J]. Journal of Intelligent Material Systems & Structures, 2012, 23(13): 1433-1449.

[10]ZHENG R, NAKANO K, HU H, et al. An application of stochastic resonance for energy harvesting in a bistable vibrating system [J]. Journal of Sound & Vibration, 2014, 333(12): 2568-2587.

[11]孫舒，曹樹謙．穩態壓電懸臂梁發電系統的動力學建模及分析[J]．物理學報，2012，60(21):103- 114．

SUN Shu，CAO Shuqian．Dynamic modeling and analysis of a bistable piezoelectric cantilever power generation system[J]．Acta Physica．Sinica，2012，60( 21) : 103-114．

[12]陳仲生，楊擁民．懸臂梁壓電振子寬帶低頻振動能量俘獲的隨機共振機理研究[J]．物理學報，2011,6(7)：1-7．

CHEN Zhongsheng, YANG Yongmin. Stochastic resonance mechanism for wideband and low frequency vibration energy harvesting based on piezoelectric cantilever beams [J].Acta Physica Sinica,2011,6(7):1-7．

[13]賈尚帥，孫舒，李明高．基于諧波平衡法的雙穩態壓電發電系統非線性振動特性研究[J]．振動與沖擊,2014,33(6):170-173.

JIA Shangshuai, SUN Shu, LI Minggao. Non-linear vibration analysis of bistable piezoelectric power generation system based on harmonic balance method [J]. Journal of Vibration and Shock, 2014, 33(6): 170-173.

[14]FOISAL A R M, HONG C, CHUNG G S. Multi-frequency electromagnetic energy harvester using a magnetic spring cantilever [J]. Sensors & Actuators A Physical, 2012, 182(15): 106-113.

[15]TEHRANI M G,ELLIOTT S J.Extending the dynamic range of an energy harvester using nonlinear damping [J]. Journal of Sound & Vibration, 2014, 333(3):623-629.

[16]崔巖，王飛，董維杰，等．非線性壓電式能量采集器[J]．光學精密工程，2012,20(12):2737-2743．

CUI Yan，WANG Fei，DONG Weijie，et al. Nonlinear piezoelectric energy harvester [J]. Optics and Precision Engineering，2012,20(12): 2737-2743．

[17]高毓璣，冷永剛， 范勝波，等．彈性支撐雙穩壓電懸臂梁振動響應及能量采集研究[J]．物理學報，2014,63(9)：1-13.

GAO Yuji， LENG Yonggang，FAN Shengbo，et al. Studies on vibration response and energy harvesting of elastic-supported bistable piezoelectric cantilever beams [J]. Acta Physica Sinica,2014,63(9):1-13.

[18]陳仲生，駱彥廷，楊擁民．非線性壓電振動能量俘獲行為建模及其不同參數影響機理研究[J]．國防科技大學學報，2013,35(2)：154-158．

CHEN Zhongsheng，LUO Yanting，YANG Yongmin. Modeling of nonlinear piezoelectric vibration energy harvesting behaviors and the effects of its different parameters [J]. Journal of National University of Defense Technology，2013,35(2): 154-158．

[19]李海濤，秦衛陽．雙穩態壓電能量獲取系統的分岔混沌閾值[J]．應用數學和力學,2014,35(6):652-662.

LI Haitao，QIN Weiyang.Bifurcation and chaos thresholds of bistable piezoelectric vibration energy harvesting systems [J]. Applied Mathematics and Mechanics, 2014, 35(6): 652-662.

[20]韓研研，曹樹謙，孫舒，等．考慮幾何非線性時雙穩態壓電懸臂梁響應分析[J]．壓電與聲光，2014,36(1)：132-139．

HAN Yanyan，CAO Shuqian，SUN Shu，et al. Response analysis of bistable piezoelectric cantilever beam considering geometric nonlinearity [J]. Piezoelectrics & Acoustooptics，2014,36(1): 132-139．

[21]王嘉賦，劉鋒，王鈞義，等．隨機共振系統輸入閾值的頻率特性[J]．物理學報，1997,46(12)：2305-2312．

WANG Jiafu，LIU Feng，WANG Junyi，et al．Frequency characteristics of the input thresholds of stochastic resonant systems[J]．Acta Physica Sinica，1997,46(12)：2305-2312．

[22]陳紹偉，王子，魏剛．基于壓電能量收集技術的無線傳感器節點設計[J]．計算機測量與控制,2014,22(3)：952-955．

CHEN Shaowei，WANG Zi，WEI Gang．Design of wireless sensor node based on piezoelectric energy harvesting technology[J]．Computer Measurement & Control, 2014,22(3)： 952-955．

[23]孟慶春，陳光柱．自供電無線傳感網絡節點設計[J]．儀表技術與傳感器,2012,(7)：102-104．

MENG Qingchun,CHEN Guangzhu．Design of self-powered wireless sensor network node [J]. Instrument Technique and Sensor,2012,(7): 102-104．

(編輯：張楠)

Power supply capability analysis of piezoelectric vibration generator with bistable under wide frequency excitation

HE Qing1,MAO Xin-hua1，2,CHU Dong-liang1

(1.Key Laboratory of Condition Monitoring and Control for Power Plant Equipment,North China Electric Power University，Beijing 102206，China; 2.Beijing Chonglee Machinery Engineering Co.,Ltd,Beijing 101111,China)

Abstract:In order to explore a piezoelectric vibration generator with bistable supplying power for the wireless sensor node under wide frequency excitation, dynamical model under random vibration excitation was built. And accordingly the piezoelectric vibration generator was simulated with bistable output response and voltage under different motion state. The incentive condition of the piezoelectric vibration generator was explored with bistable running in high energy orbit.Structure parameters of the piezoelectric vibration generator with bistable were optimized.Electricity demand of sensor network nodes and power production ability of piezoelectric vibration generator with bistable were analyzed.The results of imitation and experiment indicate that the output average power of the piezoelectric vibration generator with bistable is about 3.8 mW under the specific frequency band excitation. It is able to meet the power demand of the wireless sensor network node.

Keywords:vibration; wide frequency; energy harvesting; generator;bistable; dynamic response

收稿日期:2015-06-15

基金項目：中央高校基本科研業務費專項資金資助項目(13XS13)

作者簡介：何青(1962—)，男，博士，教授，博士生導師，研究方向為電力設備狀態監測與故障診斷； 毛新華(1975—)，男，博士研究生，研究方向為電力設備狀態監測與故障診斷、振動能量收集； 褚東亮(1984—)，男，博士研究生，研究方向為電力設備狀態監測與故障診斷。

通信作者:毛新華

DOI:10.15938/j.emc.2016.07.003

中圖分類號:TM 619

文獻標志碼:A

文章編號:1007-449X(2016)07-0017-07