基于等間距修正拓展雙曲線法的垃圾填埋路基沉降預測分析

王海英+常肖+阮祺

摘要：結合西咸北環線垃圾填埋高速公路建設項目，以路基沉降監測數據為依據，分析了等間距修正的拓展雙曲線法曲線模型的特性，并與三點法、雙曲線法、拓展雙曲線法測算成效和現場監測數據比較，剖析得到這種方法對應的最優控制條件。最終可知，等間距修正的拓展雙曲線法預測能將填筑期觀測數據納入分析，不需要太大的數據量就能夠計算在任意最大荷載下產生的沉降量，得到較高的相關系數和較小的誤差平方和，這樣預測能反映沉降數據的波動情況，且更加簡單方便，給高速公路沉降預測提供了一個新的參考。

關鍵詞：垃圾填埋路基；沉降預測；等間距拓展雙曲線；特性分析

中圖分類號：U414.01文獻標志碼：B 文章編號：1000033X（2016）06004105

0引言

在道路的施工和運營過程中，普遍存在的弊端之一就是路基沉降[12]。目前測算路基下沉值的方法大致有3種。首先是傳統的總合分層法，該方法運用縮減后的固結方程測算固結系數，從而預測下沉規律。其次是基于Biot固結原理的數據算法模型，它基于固結原理，聯合多類地層的本構理論，推算終極下沉值和下沉特性。這2種算法因為測算理論、參數和現場實測不相符，推算成效與現場情況存在較大差異，因而很難在工程施工應用中開展。再次是依據現場數據預測日期和路基下沉值關系的線性回歸測算理論，其大致算法包括三點法、Asaoka法、指數曲線、雙曲線、泊松曲線、S曲線、擴充曲線和多類拼合模型[39]，各類模型具備其相應的實用邊界和限度：三點法必須選擇填土完成的3個同間距的時間點，并要求間距盡量寬，因此人工選點會干預其精確度；雙曲線模型必須依據填土完成之后采集的沉降值來測算，因此需滿足恒載的長期性；Asaoka法需均分時間，測算太過繁瑣。

德國在高鐵路基沉降預測中，以雙曲線法為基礎，引入荷載系數的概念，形成了拓展雙曲線法，將之應用于路基沉降預測，并取得了較好的預測效果。本文利用等分數據量，在拓展雙曲線法的基礎上，改進得到等間距修正拓展雙曲線法，結合西咸北環線垃圾填埋路基現場觀測數據，對比等間距修正的拓展雙曲線法與雙曲線、三點法、拓展雙曲線法等的預測結果，研究新方法的數據量、時間起點的合理選取等問題，以評價新方法對于中國高速公路路基沉降評估的適用性和有效性。

1等間距修正拓展雙曲線法的提出

1.1拓展雙曲線法的提出及傳統解法

拓展雙曲線方法是在常規雙曲線法中引入荷載系數拓展而成的，它假定在荷載增量、加載速率變化不大的情況下，沉降變形的增量與荷載增量成正比。該方法與傳統方法的最大區別就是將填筑期觀測數據納入分析時間段以內，其基本公式為

2新舊方法的計算對比

西咸北環線采用建筑垃圾填筑，其中包含渣土磚石、土砂漿、混凝土小塊等。表1為A匝道AK0+980斷面的沉降觀測數據，由2014年3月23日開始填土，到2014年6月20日填土完畢，填土層厚5524 mm。沉降觀測從2014年3月21日開始，到2015年2月20日為止，累計下沉值為239 mm。

如圖2所示，在0～90 d，沉降變化較大，沉降速率逐漸減小；在填土完畢1個月后，路基下沉變化量越來越小，實測線接近平穩。由表1的沉降觀測數據可知，路基沉降的數據波動較小，連續2次觀測沉降值的變化最大量為5 mm，但由于總沉降值較小，所以實際相對波動率很高。

從表2可以看出，拓展雙曲線法和新方法的相關系數遠大于三點法和雙曲線法的相關系數，且三點法和雙曲線法計算的誤差平方和也大于拓展雙曲線法和新方法，其中新方法的誤差平方和最小，可見其擬合精度是比較高的，對于A匝道AK0+980斷面來說能夠得到較好的預測效果，詳見圖3。

圖3新方法與傳統算法的擬合效果對比

3新方法的優越性

為了進一步檢驗三點修正雙曲線算法的優越性，分別運用雙曲線、三點法、拓展雙曲線法和新方法對A匝道AK1+050、AK1+120和D匝道DK0+550、DK0+620、DK0+690斷面的實測值進行計算，分析計算結果，可以得出以下結論。

（1）在對填筑期的數據進行預測時，三點法和雙曲線法的相關系數都過小，同時誤差平方和過大，這說明三點法和雙曲線法不適合對填筑期的數據進行預測。

（2）新方法測算所得的相關系數均高于雙曲線法和三點法的相關系數，且滿足相關系數大于0.92的條件；同時，新方法測算數據與沉降現場數據的誤差平方和均小于拓展雙曲線法、雙曲線法和三點法，這說明新方法的擬合精確度大于其他幾種方法。

（3）新方法測算所得數據很好地保留了拓展雙曲線法的優點，在保證荷載系數的同時，將填筑期觀測數據納入分析的時間段以內，計算得出任何時間的沉降量，同時能夠很好地反映數據波動情況。

4新方法的特性探求

與普通算法相比，新方法的測算結果與現場沉降數據較為一致。本節通過分析計算AK0+980斷面的沉降觀測數據，對新方法的特性進行研究，探討數據量T、時間起點t0對相關系數、誤差值的影響。

4.1數據量T對測算成效的影響

當時間起點相同時（取填筑開始日期，即t0=0），變動數據量T，運用新方法進行計算，表3和圖4給出了計算結果。分析可得以下結論。

（1）當數據量T不同時，預測結果的相關系數都能滿足大于0.92的要求，并且相關系數都接近1，說明擬合性好；同時，預測結果的誤差平方和均較小，說明預測精度高，其中T=16時，預測結果誤差平方和最小。

（2）保持t0相同時，T越大，參數α越大，β越小。當T=8～20時，沉降測算線隨著T的增大不斷貼近現場觀測沉降線；而當T=20～30時，隨著其不斷增大，沉降測算線遠離現場沉降線。

（3）由表2、3可知，當觀測期較短時 ，新方法與其他預測方法相比擬合效果更好。這主要是由于它保留了荷載系數概念，把填筑區的觀測數據納入分析段的原因；而其他方法只利用了恒載區的觀測數據。

（4）采用新方法預測時，若觀測時間不足（t160 d），T盡可能取較大值；若觀測時間足夠長，數據量T沒有必要取很大，建議T=16。

4.2時間起點t0對測算成效的影響

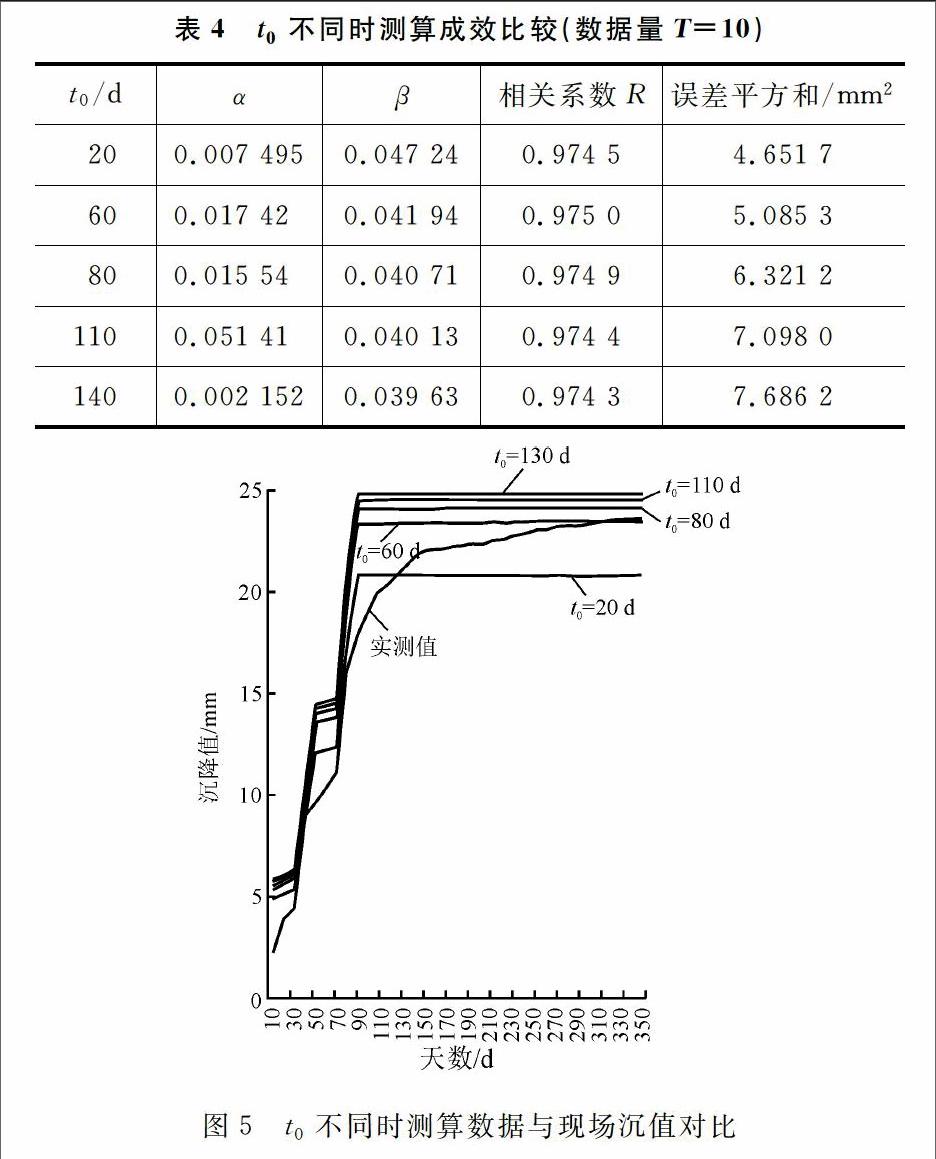
當T=10不變，分別取實測曲線中填筑期沉降激增的時間點，即2014年4月20日、2014年5月30日和2014年6月20日，以及恒載期的2個時間點2014年7月20日、2014年8月20日，進行計算，對比分析固定時間間隔，取不同的時間起點時新算法的測算成效，結果如表4和圖5所示。

由表4和圖5的測算可得到以下幾點結論。

（1）選擇不同的時間起點時，預測曲線的相關系數都能滿足大于092的要求，這說明擬合性好；但是，隨著時間起點的延后，預測的誤差平方和也在增大，這說明選點的差異會影響預測的精度。

（2）選擇恒載期的數據作為測算數據時，并沒有增加預測的精度，這說明新方法不受填筑期和恒載期的影響，對所有的數據都能進行利用并得到較高的擬合性和精度。

（3）隨著t0的增加，預測曲線反映沉降數據的波動情況沒有改變；同時，采用新方法預測時，時間起點應盡量小，這里建議t0=0 d。

5結語

（1）通過等分數據量對拓展雙曲線法的傳統解法進行了改進，推算得出了α、β的求解公式。

（2）通過實例分析可知：新方法能夠克服其他方法不能對填筑期數據進行預測的缺點，并能夠很好地反應數據的波動情況，不需要很大的數據量就能進行預測，測算所得的相關系數滿足要求，誤差平方和均較小，與三點法、雙曲線方法、拓展雙曲線法相比具有一定的優勢，驗證得出新方法能夠適用于量級小、波動大的數據。

（3）對新方法的特性進行了研究，取不同時間起點和不同數據量進行了對比，計算并得出滿足新方法預測精度的T和t0，建議T=16、t0=0 d。

參考文獻：

[1]牛永宏，郭滕滕，王鑫.建筑垃圾回填路基施工技術研究[J].筑路機械與施工機械化，2014，31（9）：4952.

[2]許興旺，李肖倫.濕陷性黃土地區客運專線路基沉降觀測分析[J].巖土力學，2010，31（1）：233236.

[3]王豐勝.基于理論和實測的路基沉降混合預測方法[J].長安大學學報：自然科學版，2011，31（4）：3438.

[4]朱潤霞.基于智能計算的高速鐵路路基沉降預測系統研究[D].哈爾濱：哈爾濱理工大學，2015.

[5]張欣.沉降預測的方法和適用性研究[J].交通建設與管理，2015（10）：8184.

[6]王小兵.高速公路路基工后沉降新型組合推算方法[J].山西建筑，2014，40（24）：148150.

[7]金亮星，李小剛.泊松曲線法在填海造地道路軟基沉降預測中的應用[J].鐵道科學與工程學報，2013，10（5）：5256.

[8]肖長生，王守林，金亮星.經驗分析法在軟基沉降預測中的應用[J].鐵道科學與工程學報，2012，9（3）：7276.

[9]肖衡林，李麗華，郭小川，等.山區高填方路堤沉降預測方法[J].應用基礎與工程科學學報，2015，23（1）：154161.