基于PE方法的數據中心需量費用優化算法

黃焱，王鵬，謝高輝

?

基于PE方法的數據中心需量費用優化算法

黃焱1,2，王鵬3，謝高輝4

(1. 中國科學院成都計算機應用研究所，四川成都 610041；2. 中國科學院大學，北京 100049； 3. 西南民族大學計算機科學與技術學院，四川成都610041；4. 廣州五舟科技股份有限公司，廣東廣州 510000)

數據中心的電費包含需量費用和用量費用2個部分，以往的數據中心電費優化研究通常未考慮需量費用。在滿足服務質量和響應時間的約束條件下采用PE(partial execution)方法可以減少峰值功率，從而降低需量費用。通過對時間、外部負載、服務質量約束、響應時間約束進行建模，構建電費優化問題的模型，提出基于PE方法的需量費用優化算法PEDC（partial execution demand charge)，在高負載時間段執行PE方法減小峰值功率以降低需量費用并降低用量費用，從而降低數據中心的總電費。通過與4種算法進行比較，并構造準確預測的負載數據對PEDC算法性能進行測試，PEDC算法可以降低數據中心運營總電費5.9%~12.7%，提升集群使用率1.32倍。

PE方法; 需量費用; 用量費用; 能耗費用優化

1 引言

近年來，云計算、大數據、移動互聯網等信息產業的前端領域高速發展，數據中心作為信息產業的后端基礎設施在集群數量和集群規模上呈現出快速增長趨勢。谷歌、微軟公司的數據中心服務器數目均超過100萬臺，阿里的“飛天”集群規模超過5 000臺[1]，全球TOP500超級計算機的CPU核數與計算性能的年增長率達53%[2]，IDC預測到2017年全球數據中心的數量將達到860萬個[3]。

數據中心的能耗巨大，2010年美國數據中心消耗的電能占其全國總能耗的1.7%~2.2%，2012年其消耗的電能比2011年增長19%，2013年其數據中心每小時消耗910億度電，預計到2020年，數據中心消耗的電能將占全球能耗的8%，碳排放量為全球碳排放量的2.6%[4]，電費成為數據中心最大的運營開支。假定數據中心基礎設施的折舊期為15年，服務器的折舊期為3年，則數據中心的電費占運營成本的41.6%[5]，因此，數據中心功耗優化是研究的熱門領域。文獻[6]對數據中心能耗控制進行綜述，將能耗控制方法劃分為硬件和算法2個層級：在硬件層可通過低功耗多核處理器芯片[7]、直流電源、高效制冷設備等硬件技術降低數據中心的功耗[8]；在算法層可通過DVFS (dynamic voltage and frequency scaling)、DFS(dynamic frequency scaling)和動態節點控制技術等方法調節CPU的電壓、頻率從而對數據中心進行節點級功耗控制[9]，也可以通過動態調節數據中心的運行節點數目，提高服務器使用率、減少處于閑置狀態的節點數量，從而降低數據中心的功耗[10]，進行數據中心級功耗控制。

目前相關研究多利用電價在時間和地理位置上的差異對電費進行優化。文獻[11~13]利用電價在地理位置上的差異，將負載分配到價格較低的區域執行，對分布式數據中心的負載分配進行調控，從而對電費進行優化；文獻[8, 14, 15]利用電價在時間上的波動對電費進行優化，將負載盡量安排在低電價時段執行，減少高電價時段的執行；在對電費進行優化的同時還可對服務質量(QoS, quality of service)[12, 13]、對智能電網的影響[16, 17]、碳排放量[18]、UPS的使用[19]、動態服務定價[20]等第二優化目標進行優化，文獻[21]對其進行了詳細綜述。

上述研究中，電費均是根據數據中心消耗的電量(kWh)和電價求得，而其電價大多采用智能電網實時的零售價格，這與數據中心的實際情況不符。由于數據中心長期消耗巨大的電能[4]，一般都與電力運營商簽署長期用電合同[22]，按照長期合同電價進行結算，而不是根據實時的零售電價進行結算，這樣既可以使數據中心運營商合理地對業務運營進行優化，避免由于電價波動給數據中心增加電力成本，也可以使電力供應商有效掌握用電需求，合理規劃電力的生產與分配，提高電網的穩定性。通過對多個地區大型用電單位的實際電力供應合同進行研究，發現電費由用量費用(EC, energy charge)和需量費用(DC, demand charge)構成。用量費用是用電單位為所消耗的電量(kWh)支付的費用，是大多數研究采用的常規電費計算方式；需量費用是用電單位為用電時間段中的峰值功率支付的費用(kW)。目前對于數據中心用量費用優化的研究已經很充分，但對其需用量費用優化的研究很少。本文基于此展開研究，使用PE(partial execution)方法減少數據中心的峰值用電量，從而降低用量費用。

本文首先對數據中心能耗費用優化的相關研究進行分析，介紹電價方案、PE方法、服務質量等背景知識，發現目前的研究大多只對數據中心的用量費用進行優化，沒有考慮需量費用，而數據中心的需量費用一般比用量費用高得多，是電費的主要部分，因此提出使用PE方法降低數據中心的峰值用電量的核心思想；然后對系統的時間、外部負載、服務質量約束、響應時間約束等進行建模，構建電力費用優化問題模型，提出PEDC算法；最后將PEDC算法與4種算法進行比較，并通過構造準確預測的負載數據對PEDC算法的性能進行測試，實驗結果表明PEDC算法可以有效降低數據中心的需量費用和用量費用，并提高集群使用率。

本文主要創新點如下。

1) 采用數據中心實際使用的電費合同，綜合考慮需量費用和用量費用，計費模式符合數據中心的實際情況，將數據中心電費優化劃分為降低峰值功率和降低用電量2個問題。

2) 使用//隊列模型對等待執行的負載建模，運行節點處于滿負載的狀態，避免空閑節點的電量消耗，提高節點的利用率。

3) 在算法優化過程中，同時考慮服務質量約束和響應時間約束2個條件。

2 背景知識

本文的核心目標是根據外部負載的情況，在滿足服務質量約束[24]和負載響應時間約束的條件下，確定執行PE方法的時間段，降低數據中心的峰值用電量，減少其需量費用。本節對文中涉及的電價方案、PE方法和服務質量等關鍵的背景知識進行講解。

2.1 電價方案

零售電價是電力運營商按照單位時間用電量($kWh)的定價方案，為了保障電網中零售用電的負載均衡，保障電網安全，電力運營商會根據電力負載制定不同地區和不同時間段的零售電價。數據中心是長期、高負載用電單位，與電力運營商簽訂長期用電合同，不使用零售電價。通過對電力運營商的長期用電合同[25]的分析可以發現長期電力合同從用電總量、峰值功率2個方面與用戶進行約定，以15 min作為單位時間段進行統計。用電總量是總計費時間內用戶消耗的電量(kWh)，峰值功率是所有時間段(15min)中最大的平均功率(kW)，峰值功率越大，電力運營商需要為其投入更多的基礎設施以保障穩定供電，用戶因此需要支付越多的需量費用。需量費用可能比用量費用大很多，例如，在美國GA地區某用電單位的峰值功率為10 MW、平均功率為6 MW，根據如表1所示的電價可求得其月用量費用為$38 400，月需量費用為$147 312，需量費用是電費的主要支出。

因此，合同電價包含用量價格和需量價格2個部分，表1列出了6個區域的合同電價，從中可以發現這些區域的需/用數值比存在較大差異，GA區域需/用數值比最大，OR區域需/用數值比最小，5.4節對各個區域分別進行實驗，研究區域電價差異對數據中心電費的影響。

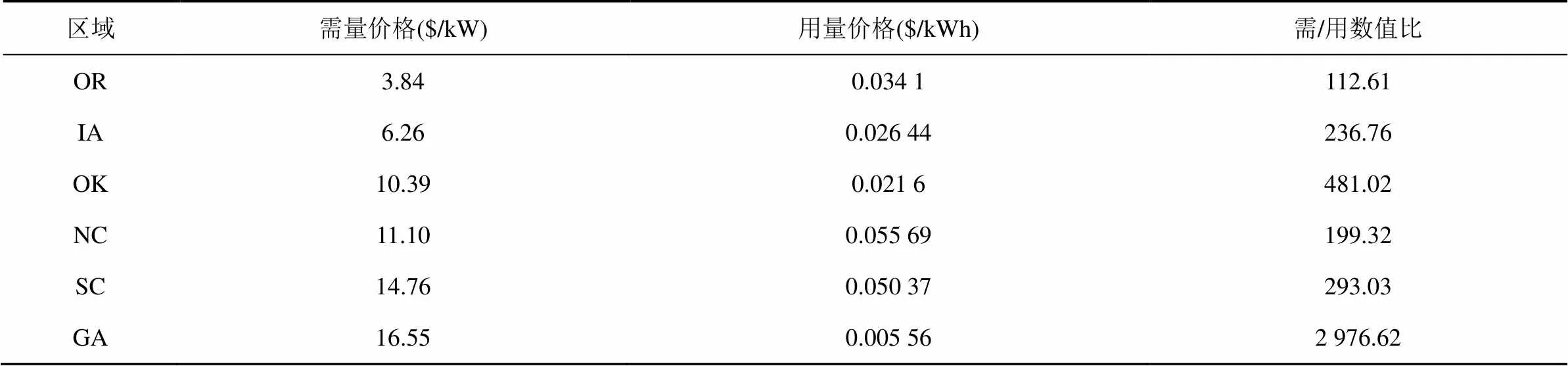
表1 6個區域的合同電價

2.2 PE方法

Web搜索、金融服務、仿真模擬等類型業務的計算結果精度取決于計算任務量，計算時間越長，計算越充分，其計算結果越精確。PE方法正是這樣一種通過對不完全執行任務來減少負載執行量的方法[23]，適用于可接受近似計算結果的交互式類型負載的計算。本文采用PE方法減少負載高峰期的運行負載數，從而降低需量費用。

以搜索引擎類任務為例，當搜索引擎接收到某個關鍵詞的搜索任務時，會首先在緩存中進行檢索，如果沒有在緩存中檢索到，則會將搜索任務發送到檢索服務器集群，每臺檢索服務器對大量的文件進行并發的檢索操作。搜索結果的精準度與檢索的文檔數量有關，對全部文件進行檢索所得到的結果為最優結果，但花費的時間會超出響應時間的限制；如果采用PE方法對部分文件進行檢索，會減少運行的負載數目，縮短運行時間，從而得到近似的搜索結果。

微軟Bing搜索服務的質量與其后端計算執行率的關系如圖1所示[23]，從圖中可以發現，當負載執行率為50%時的搜索服務質量為0.82，當進一步提高負載執行率時，服務質量的提高速度變慢，無需將負載完全運行即可獲得可接受的近似計算結果。因此在滿足計算精度要求的前提下在高負載時間段使用PE方法可以降低數據中心的峰值用電量、降低用量費用。

2.3 服務質量

服務質量表示使用PE方法的交互式應用響應質量與完全執行的響應質量的比值，是此類應用最重要的執行評價指標之一。在如圖1所示的Bing搜索服務中，每個負載執行比率對著相應的服務質量。為了對問題模型進行簡化，可按照服務質量將服務分為高質量服務和低質量服務，這樣可以使用二進制數0和1來表示服務質量。交互式應用對其高質量服務占比的要求為服務質量約束，搜索引擎服務一般要求其高質量服務占比超過95%[23]。

3 系統模型

本文采用非連續時間模型，根據數據中心電費合同以15 min為時間間隔將1天分為96個時間段，即，對時間段分別計算負載數量、平均功率、耗電量、電費等參數并設定運行節點數目。數據中心由同構節點組成，時間段的運行節點數目由負載大小以及能耗優化策略決定，節點一旦運行即處于滿負荷運行狀態，因此每個節點的功耗相同。本文假定數據中心的PUE值固定，當運行節點數增加或減小時，制冷設備的功耗相應地增加或減少。數據中心所處理的負載為交互式類型負載，有嚴格的響應時間要求。

3.1 服務質量約束

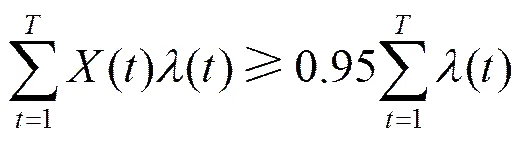
(2)

3.2 響應時間約束

本文用//排隊模型來定義數據中心內等待處理的負載任務，設時間段的外部負載量為，運行節點數據數為，節點服務率為，負載在數據中心始終處于等待狀態，則負載的平均等待時間。設定負載響應時間為，結合式(2)可得響應時間的約束條件為

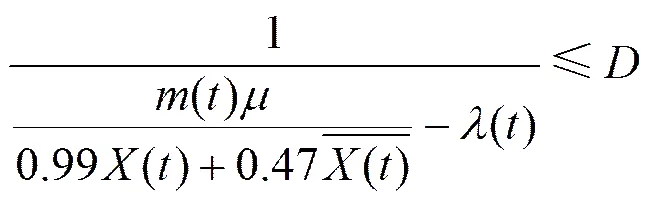
3.3 電力費用模型

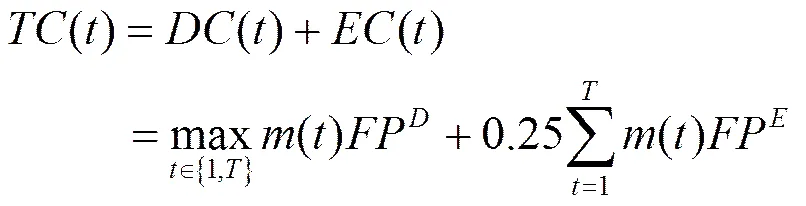
數據中心能耗費用優化問題P1表示如下

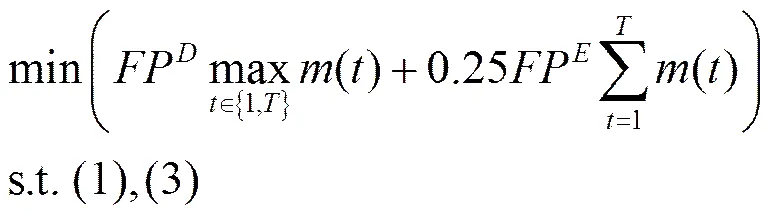
4 求解方法

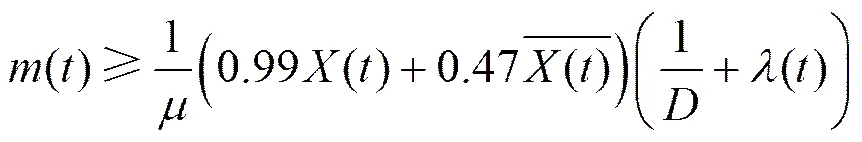
(7)

4.1 求解需量費用()的最小值

由式(6)可得

(8)

4.2 求解用量費用()的最小值

由式(6)可得

(9)

4.3 PEDC算法流程

PEDC算法首先在滿足服務質量約束(1)的條件下將負載最大時段的運行模式設置為低質量服務模式，再根據約束條件(8)求解運行節點數，從而根據決定變量的數值求解數據中心電費的最小值，PEDC算法基本流程如下：

if 滿足服務質量約束條件(1) then

將()設置為1

else

將()設置為1

end if

end while

PEDC算法的計算時間和所需空間取決于2個部分：第1部分對已知負載使用PEDC算法階段，與這個階段所包含的時間段的個數有關；第2部分對未知負載使用PEDC算法階段，與這個階段所包含的時間段的個數有關，這2部分需要不斷地確定峰值負載所在位置，其時間復雜度和空間復雜度都為。

5 實驗驗證

5.1 實驗參數說明

本文設定數據中心由同構服務器組成，服務器處于空閑狀態時的功率為400 W，處于滿負荷狀態時的功率為750 W，每個節點每秒可處理9個外部負載，負載的最大響應時間為0.01 s。外部負載采用某數據中心的真實訪問數據集，該數據集包含2015年3月15日~4月11日共計28天的外部訪問數據(DATA1)，如圖2所示，可以看出外部負載的周期性較為規律。

5.2 對比算法

本文選取3月15日~3月21日共計7天的負載數據，使用PEDC算法計算數據中心28天的電費，對PEDC算法的性能進行評估，并分別與NOPE、RAND、BEST和CUPE算法的控制效果進行對比，這5種算法的說明如下。

PEDC：該算法使用本文構造的基于PE方法的數據中心電費優化算法，在已知7天外部負載數據的條件下計算數據中心28天的運行電費。

NOPE：該算法使用負載等待隊列模型，但不使用PE方法，即所有時間段數據中心均運行于高質量服務模式。

RAND：該算法使用負載等待隊列模型并使用PE方法，PE方法的執行時間從執行時間段中隨機選取。

BEST：該算法在已知28天負載數據的情況下使用PEDC算法計算數據中心的運行電費，所得結果是PEDC算法最理想的優化結果。

由于根據7天負載數據預測28天的負載與真實數據存在偏差，將4組相同的7天真實負載數據生成一組28天的負載數據(DATA2)，來模擬完全準確預測負載的情況，對PEDC算法的性能進行測試。PEDC-1和BEST-1算法是使用負載數據DATA2的PEDC算法和BEST算法。

5.3 運行功率與運行電費分析

求解各算法在負載運行中的最大運行節點數和平均運行節點數，得到數據中心的峰值功率和平均功率，如圖3所示。根據3.3節的電費模型，計算數據中心的需量費用、用量費用和總電費，如圖4所示，本節使用表1中SC區域的電價進行實驗分析。

5.3.1 運行功率分析

由于NOPE算法不使用PE方法對峰值功率進行調節，所有時間段數據中心均運行在高質量服務模式，所有負載均被完整地運行，本文將其峰值功率作為基準峰值功率，將其平均功率作為基準平均功率。由于RAND算法隨機選取PE方法的執行時間段，沒有抽取到峰值負載時間段運行PE方法，因此峰值功率等于基準峰值功率。CUPE算法模型中所有節點始終處于運行狀態，存在空閑運行功率，當節點負載增加，運行功率隨之增加，CUPE算法的峰值功率與PEDC算法的峰值功率相等，但平均功率是PEDC算法平均功率的1.7倍。PEDC算法的集群使用率為CUPE算法的2.32倍。

PEDC算法的峰值功率比基準峰值功率降低了13.57%，低于BEST算法19.43%的降低率，2個數值之間存在差距的原因是預測負載數據與實際負載數據之間存在一定的差異。PEDC-1算法和BEST-1算法使用負載數據DATA2來模擬完全準確預測負載數據的情況，數據顯示PEDC-1算法和BEST-1算法的峰值功率相同，表明負載數據預測越準確，PEDC算法的能耗優化效果越好；當負載數據得到精確預測時，PEDC算法對峰值功率的優化可以達到理論最優值。

PEDC、BEST、RAND算法的平均功率均比基準平均功率降低約2.62%，降低比例與5%的負載運行于低質量服務模式所減少的平均功率相符。

5.3.2 運行電費分析

將NOPE算法的需量費用作為基準需量費用，用量費用作為基準用量費用，總電費作為基準總電費。數據中心的需量費用由峰值功率決定，用量費用由平均功率決定，PEDC、BEST、RAND、PEDC-1、BEST-1算法的需量費用與基準需量費用的關系以及用量費用與基準用量費用的關系與運行功率部分的分析相同。CUPE算法的需量費用等于基準需量費用，其用量費用是PEDC算法用量費用的1.7倍。

PEDC算法的總電費比基準總電費降低了8.45%，高于RAND算法1.23%的降低率，低于BEST算法11.57%的降低率。使用負載數據DATA2的PEDC-1算法和BEST-1算法的總電費降低率相等。CUPE算法的總電費是PEDC算法總電費的1.35倍。

5.4 區域電價對電費的影響

為了驗證不同區域電價對數據中心總電費的影響，本節用表1中6個區域的合同電價對PEDC算法進行實驗，并與NOPE、BEST算法進行比較。

圖5所示為在相同的負載數據(DATA1)下，6個區域分別用PEDC、NOPE、BEST算法計算所得的總電費。設NOPE算法求得的總電費為基準總電費，使用PEDC算法總電費降低比率為5.9%~12.7%，使用BEST算法總電費降低比率為7.34%~18.1%。GA區域降低比率最高，OR區域降低比率最低，這是由于PEDC、BEST算法可大幅降低需量費用，對用量費用的降低率較為固定，因此需量費用/用量費用數值比越高，總電費降低比越高。

5.5 服務質量約束對電費的影響

本節使用PEDC算法通過調節服務質量約束和服務質量，研究其對數據中心電費的影響。首先，調節服務質量約束的數值，依次取0.95、0.9、0.85、0.8，需量費用、用量費用和總電價與的關系如圖6所示。由于隨著數值的減小，運行負載總數成比例減少，因此PEDC算法和BEST算法的用量費用與呈線性關系；由于預測負載數據與實際負載數據之間存在差異，PEDC算法的需量費用減少較BEST算法更為緩慢；需量費用和用量費用疊加即得總電費。

6 結束語

本文通過研究數據中心實際的電費合同，發現其電費包含需量費用和用量費用2個部分，在滿足服務質量和響應時間的條件下，通過在負載高峰期使用PE方法，可以降低數據中心的峰值電量，在降低需量費用的同時降低用量費用，從而減少數據中心運行的總電費。本文提出基于PE方法的數據中心需量費用優化算法PEDC，并與4種算法進行實驗比較，實驗數據表明使用PEDC算法的總電費比使用NOPE算法降低5.9%~12.7%，集群使用率為使用CUPE算法的2.32倍，PEDC算法可用于對搜素引擎、金融計算等交互式應用領域的數據中心電費進行優化，可與數據中心負載分配方法[26]結合使用，進一步降低數據中心的能耗費用。

[1] [EB/OL]. http://www.csdn.net/article/2013-10-30/2817347-awdc2013- feitian5k.

[2] [EB/OL].http://www.top500.org/lists.

[3] [EB/OL].http://www.idc.com/getdoc.Jsp?containerid=prus25237514.

[4] GAO PX, CURTIS AR, WONG B, et al. It's not easy being green[J]. ACM SIGCOMM Computer Communication Review, 2012, 42(4): 211-222.

[5] HAMILTON J. Cooperative expendable micro-slice servers(CEMS): low cost, low power servers for internet-scale services[C]//CIDR’09. c2009.

[6] BELOGLAZOV A, BUYYA R, LEE YC, et al. A taxonomy and survey of energy-efficient data centers and cloud somputing systems[J]. Advances in Computers, 2011, 82(2): 47-111.

[7] BARROSO LA, H?LZLE U. The case for energy-proportional computing[J]. IEEE Computer, 2007, 40(12): 33-37.

[8] YAO Y, HUANG L, SHARMA A, et al. Data centers power reduction: a two time scale approach for delay tolerant workloads[C]//IEEE INFOCOM. c2012: 1431-1439.

[9] GANDHI A, HARCHOL M, DAS R, et al. Optimal power allocation in server farms[C]//ACM SIGMETRICS. c2009:157-168.

[10] LIN M, WIERMAN A, ANDREW LL, et al. Dynamic right-sizing for power-proportional data centers[J]. IEEE/ACM Transactions on Networking, 2013, 21(5): 1378-1391.

[11] RAO L, LIU X, XIE L, et al. Minimizing electricity cost: optimization of distributed internet data centers in a multi-electricity-market environment[C]//IEEE INFOCOM. c2010:1-9.

[12] RAO L, LIU X, ILIC MD, et al. Distributed coordination of internet data centers under multiregional electricity markets[J]. Proceedings of the IEEE, 2012, 100(1): 269-282.

[13] LI J, LI Z, REN K, et al. Towards optimal electric demand management for internet data centers[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 183-192.

[14] LUO J, RAO L, LIU X. Temporal load balancing with service delay guarantees for data center energy cost optimization[J]. IEEE Transactions on Parallel and Distributed Systems, 2014, 25(3): 775-784.

[15] LUO J, RAO L, LIU X. Data center energy cost minimization: A spatio-temporal scheduling approach[C]//IEEE INFOCOM. c2013: 340-344.

[16] WANG H, HUANG J, LIN X, et al. Exploring smart grid and data center interactions for electric power load balancing[J]. Performance Evaluation Review, 2014, 41(3): 89-94.

[17] ZHOU Z, FANGMING L, ZONGPENG L, et al. When smart grid meets geo-distributed cloud: an auction approach to datacenter demand response[C]//IEEE INFOCOM. c2015.

[18] ZHANG Y, WANG Y, WANG X. Capping the electricity cost of cloud-scale data centers with impacts on power markets[C]//HPCD’11. c2011. 271-272.

[19] GUO Y, FANG Y. Electricity cost saving strategy in data centers by using energy storage[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(6): 1149-1160.

[20] 王巍, 羅軍舟, 宋愛波. 基于動態定價策略的數據中心能耗成本優化[J]. 計算機學報, 2013, 36(3): 599-612.

WANG W, LUO J X, SONG A B. Dynamic pricing based energy cost optimization in data center enviroments[J]. Chinese Journal of Computers, 2013, 36(3): 599-612.

[21] RAHMAN A, LIU X, KONG F. A survey on geographic load balancing based data center power management in the smart grid environment[J]. IEEE Communications Surveys & Tutorials,2014, 16(1): 214-233.

[22] MALTZ DA. Challenges in cloud scale data centers[C]//ACM SIGMETRICS. c2013: 3-4.

[23] HE Y, ELNIKETY S, LARUS J, et al. Zeta: Scheduling interactive services with partial execution[C]//ACM SOCC.c 2012: 12-25.

[24] XU H, LI B. Reducing electricity demand charge for data centers with partial execution[C]// ACM e-Energy. c2014: 51-61.

[25] [EB/OL].http://www.cs.cityu.edu.hk/~hxu/share/Contracts.zip.

[26] 金嘉暉, 羅軍舟, 宋愛波. 基于數據中心負載分析的自適應延遲調度算法[J]. 通信學報, 2011, 32(7): 47-56.

JIN J H, LUO J Z, SONG A B. Adaptive delay scheduling algorithm based on data center load analysis[J]. Journal on Communications, 2013, 32(7): 47-56.

Optimizing demand charge of data center base on PE method

HUANG Yan1,2, WANG Peng3, XIE Gao-hui4

(1. Chengdu Institute of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China; 3. School of Computer Science and Technology, Southwest University for Nationalities, Chengdu 610041, China; 4. Guangzhou Wuzhou Technology Corporation, Guangzhou 510000, China)

Demand charge and energy charge are the two main components of data center electricity cost, previous researches have not take demand charge into consideration. PEDC algorithm was proposed by modeling time slot, workload, service quality constraint and response time constraint. With PEDC algorithm peak power was decreased by partial execution on the condition of service quality constraint and response time constraint. PE method was executed in the heavy loaded time slots to reduce peak power so as to optimize demand charge. Energy charge and total charge were also optimized. By comparing with four algorithms and with dataset accurately predicted, PEDC algorithm can reduce electricity cost by 5.9%~12.7% and improve cluster utilization 1.32 times.

PE method, demand charge, energy charge, energy cost optimization

TP393

A

10.11959/j.issn.1000-436x.2016056

2015-05-01；

2015-07-31

王鵬，wp002005@163.com

國家自然科學基金資助項目(No.60702075)；廣東省科技廳高新技術產業化科技攻關基金資助項目(No.2011B010200007)；成都市創新發展戰略研究基金資助項目(No.11RKYB016ZF)

The National Natural Science Foundation of China(No.60702075), Guangdong Science and Technology Plan of Industrial High-Technology(No.2011B010200007), Chengdu Innovation and Development Strategy Research Project (No.11RKYB016ZF)

黃焱（1982-），男，江蘇泗陽人，中國科學院成都計算機應用研究所博士生，主要研究方向為智能算法、最優化理論等。

王鵬（1975-），男，四川犍為人，西南民族大學教授、博士生導師，主要研究方向為智能算法、高性能計算等。

謝高輝（1979-），男，湖南郴州人，廣州五舟科技股份有限公司總經理，主要研究方向為高性能計算。