結合快速魯棒性特征改進ORB的特征點匹配算法

白雪冰 車進 牟曉凱 張英

摘要：針對定向二進制簡單描述符（ORB）算法不具備尺度不變性的問題，提出一種結合快速魯棒性特征（SURF）算法和ORB的改進算法。首先，利用Hessian矩陣檢測特征點的方法，使得提取出的特征點具有尺度不變性；然后，用ORB生成特征描述子；接著采用K近鄰算法進行粗匹配；最后，通過比率測試、對稱測試、最小平方中值（LMedS）定理全文中，“最小中值定理”是否應該為“最小平方中值定理”或“最小中值平方定理”更為規范些？請明確。回復：“最小中值定理”統一改為“最小平方中值定理”，英文翻譯不用動進行提純。尺度變化時，該算法比ORB的匹配精度提高了74.3個百分點，比SURF的匹配精度提高了4.8個百分點；旋轉變化時，該算法比ORB的匹配精度提高了6.6另外，根據表2的數據，此處是6.6吧？請明確。個百分點；匹配時間高于SURF低于ORB。實驗結果表明，改進算法不僅保持了ORB的旋轉不變性，而且具備了尺度不變性，在不失速度的前提下，匹配精度得到較大提高。

關鍵詞：

特征點匹配；尺度不變性；旋轉不變性；比率測試；對稱測試；最小平方中值定理

中圖分類號： TP391.9 文獻標志碼：A

0引言

圖像特征點匹配是計算機視覺的關鍵技術之一，廣泛應用于三維重建、圖像拼接、目標識別等領域[1-4]。Lowe[5]于2004年正式提出了尺度不變特征變換（Scale Invariant Feature Transform， SIFT）算法，其獨特性好，信息量豐富；但該算法的計算量大、匹配速度較慢。此后，Bay等[6]于2006年提出了快速魯棒性特征（Speeded Up Robust Feature， SURF）算法，不僅簡化了SIFT算法，而且在重復性、獨特性和魯棒性三個方面均超過或接近SIFT算法，計算速度也顯著提高。隨著計算機視覺技術的發展對特征點匹配精度和速度的要求越來越高，Roblee等[7]在2011年的 計算機視覺國際會議（Internation Conference on Computer Vision， ICCV）提出了定向二進制簡單描述符（Oriented fast and Rotated Brief，ORB）算法，其計算速度比SURF快一個數量級，比SIFT快兩個數量級，匹配性能也不遜于SURF和SIFT。

ORB是一種局部不變特征描述子，對圖像的平移、旋轉具有不變性；但卻并不具備尺度不變性[8-9]。文獻[10]利用ORB進行匹配時，采用改進的隨機采樣一致性（RANdom Sample Consensus， RANSAC）進行提純，使得匹配精度得到了提高；文獻[11]同樣在運用ORB匹配時，結合隨機采樣一致性方法，剔除錯誤匹配，并利用最小二乘估計變換參數，對圖像進行矯正；文獻[12]結合SIFT的算法思想對ORB進行改進，實現了尺度不變性。以上研究解決了一些問題，但是在使用RANSAC算法中，判定內外點距離閾值、隨機抽樣本集的次數和一致性集合的大小這3個參數需要根據不同的圖像設置不同的值，頻繁地設置參數，極大地影響了計算效率；并且文獻[12]結合SIFT的算法思想會降低計算速度，匹配精度也不高。針對上述情況，結合SURF檢測子和ORB描述子，并利用比率測試和對稱測試進行篩選，最后運用最小平方中值（Least Median Squares， LMedS）定理再次提純，從而克服了ORB不具有尺度不變性和RANSAC設置的參數較多的缺陷，并且匹配精度得到進一步提高。

1ORB算法原理

1.1特征點提取

ORB算法采用加速分割測試特征（Features from Accelerated Segment Test， FAST）算子來提取特征點，FAST角點檢測定義為：若某像素點具有與其鄰域內一定數量的像素點不同的特征時，該像素點被檢測為角點，例如在灰度圖像，某像素點周圍有足夠多像素點的灰度值均高于或低于該點的灰度值[13-14]。選取像素點H，并設該點的像素值為HP，考慮該像素點周圍的16個像素點，若在以H點為圓心，16個像素點組成的圓上有N（一般取9或者12）個連續的像素點，它們的像素點比HP+T （T為選取的閾值）大，或者比HP-T小，那么該像素點就是角點。FAST角點檢測速度快，但卻不具備旋轉尺度不變性和旋轉不變性。

FAST角點主方向運用亮度中心算法，以特征點為中心；同時作為坐標原點，在其鄰域U內計算質心位置，然后以特征點為起點，質心為終點構造向量，此向量的方向即為特征點的方向，計算過程如下所示。

區域U的矩定義為式（1）：

Mp，q=∑（x，y）∈UxpyqI（x，y）（1）

其中I（x，y）為點（x，y）處的灰度值，灰度矩設為C=（Cx，Cy）。其中：Cx=M1，0/M0，0，Cy=M0，1/M0，0，那么，FAST角點主方向為：

θ=arctan（M0，1/M1，0）（2）

1.2ORB特征描述子

ORB采用二進制的魯棒性獨立基本特征（Binary Robust Independent Elementary Feature， BRIEF）生成特征描述子[15]，BRIEF用二進制的方式描述圖像區域，大幅度減少像素間的對比量。定義S×S大小的圖像鄰域P的測試準則τ為：

τ（p；x，y）=1，p（x）

0，p（x）≥p（y）（3）

其中P（x）是圖像鄰域P在x后面的上標T是否表示轉置？那么，此處的x是否是矢量、向量或矩陣？請明確。另外，后面的x，哪個是矢量、向量或矩陣？也請一一指出。=（u，v）T處的灰度值

原內容為：“P（x）是圖像鄰域P在x=（u，v）T 處的灰度值”。現改為：“P（x）是圖像鄰域P在像素點x=（u，v） 處的灰度值，同理可知P（y）為圖像鄰域P在像素點y處的灰度值”

P（x）是圖像鄰域P在像素點x=（u，v） 處的灰度值，同理可知P（y）為圖像鄰域P在像素點y處的灰度值

。選擇n個（x，y）測試點對時，通過二進制測試準則生成n維二進制比特串的描述子，如式（4）所示：

fn（p）=∑1≤i≤n2i-1τ（p；xi，yi）（4）

其中n的選值需綜合比較計算速度、識別率和存儲效率，一般選擇64，128，256等。

由于BRIEF鄰域準則測試時僅通過單一像素進行計算，容易受噪聲影響。為了解決噪聲影響問題，ORB的測試點均采用31×31像素鄰域內的5×5子窗口，通過高斯分布選擇子窗口，再對圖像進行積分以加速計算。

上述生成的特征描述子是沒有方向的，因此使用1.1節求得的特征點質心方向作為BRIEF的主方向，使得描述子具備旋轉不變性。對于（xi，yi）處任意n個二進制準則集，定義一個2×n的矩陣：

M=x1x2…xny1y2…yn（5）

使用特征點質心方向θ對應的旋轉矩陣Rθ，構建M的一個有向形式Mθ=RθM，此時旋轉不變的BRIEF如式（6）所示：

gn（p，θ）=fn（p）|（xi，yi）∈Mθ（6）

通過貪心法則進行搜索，從計算得到的全部像素塊中選擇n個相關性最低的作為rBRIEF此處的“rBRIEF”，是否應該為“BRIEF”？請明確。旋轉不變的二進制魯棒性獨立基本特征（Rotation invariance Binary Robust Independent Elementary Feature， RBRIEF）。

1.3特征點匹配

ORB生成的特征描述子為二進制碼串形式，使用 Hamming 距離實現對特征點的匹配比較合適。

2結合SURF改進ORB的算法

由以上ORB算法原理可以看出，ORB雖然具有旋轉不變性，但卻并不具備尺度不變性，其根本原因在于FAST檢測出的特征點不含尺度不變信息，從而使得描述子不具備尺度不變性，因此，解決的辦法是使檢測出的特征點具備尺度不變信息。

2.1Hessian矩陣檢測特征點

設圖像I中某點P=（x，y），則尺度為σ的Hessian矩陣定義為：

H（P，σ）=Lxx（P，σ）Lxy（P，σ）Lxy（P，σ）Lyy（P，σ）（7）

其中Lxx（P，σ）是高斯濾波后的圖像點P在x方向的二階導數；同理，可求得Lxy（P，σ）、Lyy（P，σ）。

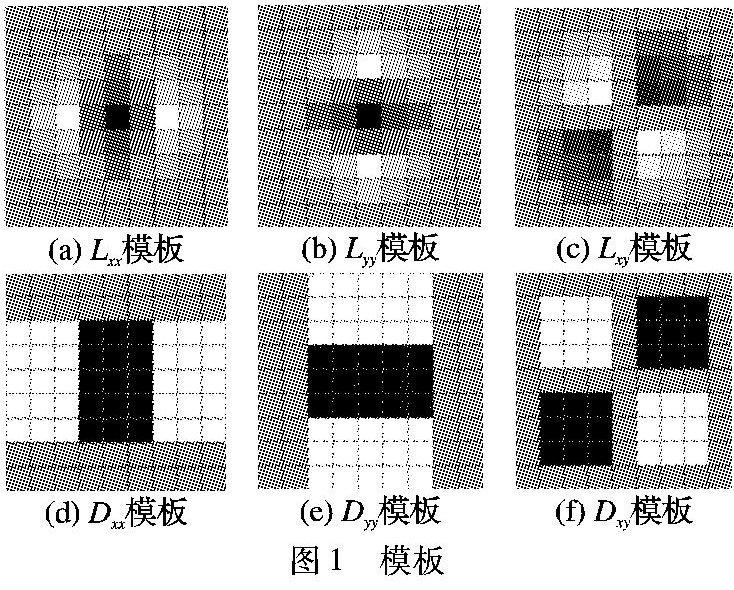
由于求Hessian時要先高斯濾波，然后求二階導數，在離散的像素點中，可以用一個模板代替，如圖1所示。此模板可以極大程度地提高計算速度，圖1頂行分別為Lxx、Lyy和Lxy；底行中用模板近似為Dxx、Dyy和Dxy表示。

圖1中白色部分的權值設為-1，黑色部分設為1，其他區域不設置權值，則計算Hessian矩陣行列式的比較精確的近似公式為：

det（H）=DxxDxx-（0.9Dxy）2（8）

其中0.9為實驗測得的比較準確的參數，進而得到每個像素點的Hessian矩陣行列式的近似值。

改變模板的大小，重復上述步驟，可以得到不同尺度下的像素點的Hessian矩陣行列式的近似值。將經過Hessian矩陣處理過的每個像素點與其三維領鄰域此處是否應該為“鄰域”？請明確。的26個點進行大小比較，如果它是這26個點中的最大值或者最小值，則保留下來，當作初步的特征點。

接著采用三維線性插值法得到亞像素級的特征點，此時的特征點即具備尺度不變性。

2.2生成特征點描述子

首先采用求FAST角點主方向的方法，計算出通過Hessian矩陣行列式求得的特征點的主方向，接著使用1.2節中求ORB特征描述子的方法，計算出特征描述子，由于2.1節求得的特征點具備了尺度不變性，并且特征描述子是在特征點的基礎上生成的，因此此時的特征描述子不僅具有旋轉不變性，而且具有尺度不變性。

2.3特征點匹配

簡單地說，K近鄰算法采用測量不同特征值之間的距離方法進行分類。令K=2，即對于每個特征點，在另一幅圖像中找到兩個候選的匹配點，其中一個是最優匹配點，另一個為次優匹配點。

2.4剔除錯誤匹配點

首先采用比率測試，其原理為：如果最優匹配點的測量距離非常小，而次優匹配點的測量距離相對較大，那么最優匹配點無疑是安全可靠的；如果兩個候選匹配點的測量距離相近，那么如果選擇其中之一作為匹配點很可能出錯，是不可靠的。比率測試正是檢查這兩個距離的比值，以除去不安全的匹配，因此對當前的匹配進行篩選，去除最有匹配和次優匹配強度響應強度大于設定閾值的匹配以及孤立的匹配。

接著采用對稱測試，令左匹配為待匹配的兩張圖從左圖到右圖的匹配，右匹配為待匹配的兩張圖從右圖到左圖的匹配，對稱測試即為對左匹配和右匹配進行檢查，輸出對稱的匹配。

最后采用最小平方中值定理提純，文獻[10]中提出使用RANSAC算法進行提純，RANSAC是一種隨機參數估計算法，性能良好，經常被采用，但其內部的3個參數需要人為設置，因此本文采用最小平方中值（Least Median Square， LMedS）算法。LMedS隨機抽選樣本中的一個子集，首先通過最小方差計算子集參數，然后計算全部樣本與該子集模型的偏差。區別于RANSAC，LMedS記錄偏差值大小居中的那個樣本的偏差，以及本次計算得到的模型參數，因此LMedS無需設定閾值來區分內點和外點。重復N次上述過程，選擇N個偏差中值最小的一個，該偏差對應的模型參數作為最終的模型參數估計值。樣本子集中樣本的個數、期望的模型誤差決定了迭代次數N的大小。最小平方中值定理克服了RANSAC的缺點，但其也存在缺點，當外點的個數占總樣本數目的比例超過50%時，就無法得到正確的模型參數，而比率測試和對稱測試經過篩選后，這個缺點也就克服了。

3實驗結果與分析

為驗證算法性能，所用電腦的處理器為Intel Core i54200，64位操作系統，內存為4.00GB，并使用Visual Studio 2013進行仿真實驗。

3.1尺度不變性實驗

為了驗證本文提出的算法的尺度不變性，以尺度變化的圖像作對比測試。其中：用ORB測試的結果如圖2所示，可以明顯看出，在尺度發生變化的時候，ORB的匹配效果并不是很好，匹配點過于集中某一部分，并且在尾巴和頭部等地方存在一些明顯的錯誤匹配；而使用本文算法測試的結果如圖3所示，得到了較為理想的實驗效果。對比圖2和圖3可以發現，本文算法克服了ORB不具備尺度不變性的缺陷，在圖像發生較大尺度變化時，仍能取得較好的匹配效果。

為了驗證本文算法在尺度變化時具有較高的匹配成功率，即匹配精度，用ORB、SURF以及本文算法分別隨機統計實驗中的5組匹配數據，如表1所示。

從表1可以看出，在尺度變化時，本文算法的匹配精度遠高于ORB的匹配精度，本文算法的平均匹配精度約為97.2%，比ORB的平均匹配精度提高了74.3個百分點，說明了該算法在尺度不變性方面的優勢。同時，本文算法比SURF的平均匹配精度提高了4.8個百分點，這要得益于提出的提純算法的優越性能。

3.2旋轉不變性實驗

本文提出的算法和ORB算法都具備旋轉不變性，為了驗證本文算法的旋轉不變性以及提出的比率測試、對稱測試和最小平方中值定理在匹配提純方面的優越性能，以旋轉圖像作為測試圖像進行比較。其中圖4是使用ORB的匹配效果，可以看出，ORB雖然具有旋轉不變性，但是由于其只是簡單地使用Hamming 距離實現特征點的匹配，因此存在錯誤匹配，例如在左下角出現了錯誤匹配。而使用本文算法進行匹配時，不僅具有旋轉不變性，而且經過有效的提純后，匹配精度得到了提高，其匹配效果如圖5所示。

為了驗證本文算法在旋轉變化時仍然具有較高的匹配精度，隨機統計實驗中的5組匹配數據，如表2所示。

從表2可以看出，圖像旋轉時，本文算法的平均匹配精度約為98.1%，比ORB的平均匹配精度提高了約6.9%6.6個百分點此處改為“提高了6.6個百分點”，通過98.1-91.5得來，或改為“提高了7.2%，通過（98.1-91.5）/91.5得來”，是否符合表達？請明確。也包括前面的中文摘要中的描述。，說明了本文算法在旋轉不變性方面同樣具有良好性能。

3.3匹配時間對比實驗

為了驗證本文算法的實時性，隨機統計實驗中的5組匹配時間數據，如表3所示。

從表3可以看出，本文算法的平均匹配時間約為180.3ms，比ORB的平均匹配時間慢了約154.8ms；但卻比SURF快了約100.6ms，說明了本文算法在實時性方面同樣具有良好性能，但是提純算法會耗費一點時間，使得匹配速度比ORB略慢。從以上實驗可以看出，本文算法具備了尺度不變性和旋轉不變性，匹配精度得到進一步提高，滿足實時性需求，有一定的實用性。

4結語

本文提出了一種結合SURF和ORB的算法，該算法克服了ORB不具備尺度不變性的缺陷，并采用比率測試、對稱測試、最小平方中值定理進一步提純，通過實驗驗證了算法的通用性以及在匹配精度方面的優越性能。由于ORB計算速度本身就很快，同時SURF提取特征點也比較快，使得匹配點經過提純后，計算速度也基本能滿足實時性的需求，但其速度不如ORB，這也是接下來要進一步研究的地方。

參考文獻：

[1]

朱琳，王瑩，劉淑云，等.基于改進快速魯棒特征的圖像快速拼接算法[J].計算機應用，2014，34（10）：2944-2947.（ZHU L， WANG Y， LIU S Y， et al. Fast image mosaic algorithm based on improved fast robust feature [J]. Journal of Computer Applications， 2014， 34（10）： 2944-2947.）

[2]

劉海燕，楊昌玉，劉春玲，等.基于梯度特征和顏色特征的運動目標跟蹤算法[J].計算機應用，2012，32（5）：1265-1268.（LIU H Y， YANG C Y， LIU C L， et al. Moving target tracking algorithm based on gradient feature and color feature [J]. Journal of Computer Applications， 2012， 32（5）： 1265-1268.）

[3]

侯毅，周石琳，雷琳，等.基于ORB的快速完全仿射不變圖像匹配[J]. 計算機工程與科學，2014，36（2）：303-310.（HOU Y， ZHOU S L， LEI L， et al. Fast fully affine invariant image matching based on ORB [J]. Computer Engineering & Science， 2014， 36（2）： 303-310.）

[4]

童宇，蔡自興.基于特征匹配的全景圖的生成[J].華中科技大學學報（自然科學版），2004，32（S1）：77-79.（TONG Y， CAI Z X. Generation of panoramic image based on feature matching [J]. Journal of Huazhong University of Science and Technology （Nature Science Edition）， 2004， 32（S1）： 77-79.）

[5]

LOWE D G. Object recognition from local scaleinvariant features [C]// Proceedings of the 1999 IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE， 1999： 1150-1157.

[6]

BAY H， ESS A， TUYTELAARS T， et al. SURF： speeded up robust feature [J]. Computer Vision and Image Understanding， 2008， 110（3）： 346-359.

[7]

RUBLEE E， RABAUD V， KONOLIGE K， et al. ORB： an efficient alternative to SIFT or SURF [C]// Proceedings of the 2011 IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE， 2011： 2564-2571.

[8]

劉銘.基于ORB算法的雙目視覺測量與跟蹤研究[D]. 哈爾濱：哈爾濱工業大學，2014：25.（LIU M. Binocular computer vision measurement and tracking research based on the ORB algorithm [D]. Harbin： Harbin Institute of Technology， 2014： 25.）

[9]

孟凡清.基于背景差分法與ORB算法的運動目標檢測與跟蹤算法研究[D].北京：北京印刷學院，2014：30-33.（MENG F Q. Study on the moving object detection and tracking based on background subtraction and ORB algorithm [D]. Beijing： Beijing Printing Institute， 2014： 30-33.）

[10]

佘建國，徐仁桐，陳寧.基于ORB和改進RANSAC算法的圖像拼接技術[J].江蘇科技大學學報（自然科學版），2015，29（2）：164-169.（YU J G， XU R T， CHEN N. Image stitching technology based on ORB and improved RANSAC algorithm [J]. Journal of Jiangsu University of Science and Technology （Nature Science Edition）， 2015， 29（2）： 164-169.）

[11]

張云生，鄒崢嶸.基于改進ORB算法的遙感圖像自動配準方法[J].國土資源遙感，2013，25（3）：20-24.（ZHANG Y S， ZOU Z R. Automatic registration method for remote sensing images based on improved ORB algorithm [J]. Remote Sensing for Land and Resources， 2013， 25（3）： 20-24.）

[12]

許宏科，秦嚴嚴，陳會茹.基于改進ORB的圖像特征點匹配[J].科學技術與工程，2014，14（18）：105-109.（XU H K， QIN Y Y， CHEN H R. Feature points matching in images based on improved ORB [J]. Science Technology and Engineering， 2014， 14（18）： 105-109.）

[13]

ROSTEN E， DRUMMOND T. Fusing points and lines for high performance tracking [C]// Proceedings of the 2005 IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE， 2005： 1508-1515.

[14]

ROSTEN E， DRUMMOND T. Machine learning for high speed corner detection [C]// ECCV06： Proceedings of the 9th European Conference on Computer Vision. Berlin： Springer， 2006： 430-443.

[15]

CALONDER M， LEPETIT V， STRECHA C， et al. BRIEF： binary robust independent elementary features [C]// ECCV10： Proceedings of the 11th European Conference on Computer vision. Berlin： Springer， 2010： 778-792.