圓形基礎地基承載力的非線性分析

陳中流

(四川遠建建筑工程設計有限公司, 四川自貢 643000)

?

圓形基礎地基承載力的非線性分析

陳中流

(四川遠建建筑工程設計有限公司, 四川自貢 643000)

【摘要】對于圓形基礎地基承載力傳統分析方法多采用的是線性的摩爾-庫侖破壞準則。而巖土材料是具有非線性的，巖土材料的線性破壞準則只是非線性破壞準則的一個特例，所以用非線性破壞準則分析圓形基礎地承載力是很有必要的。有學者根據非線性破壞準則采用單切線法進行求解，但單切線法實際上是將非線性破壞曲線線性化，并非真正意義上的引入非線性破壞準則。根據非線性破壞準則采用多切線法進行求解，并通過對地基環形單元的劃分和對計算結果的優化得到了最小的上限解。

【關鍵詞】圓形基礎；非線性破壞準則；上限解

圓形基礎在工程中廣泛運用，傳統的分析方法是根據極限平衡和線性破壞準則進行計算。在實際工程中，巖土的破壞是具有非線性性質的，線性關系只是其中的一個特例。為此，本文將探討采用非線性分析的原則對圓形基礎地基的承載力進行分析。

1Hoek-Brown強度準則

Hoek-Brown破壞準則[1-2]是基于Griffith的脆性斷裂理論提出的，表達式為：

(1)

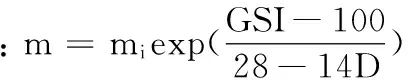
Hoek-Brown強度準則與Mohr-Coulomb強度準則相比，有如下優點[3]：

(1) 綜合考慮了巖塊強度、結構面強度、巖塊結構等多種因素的影響，能更好地反映巖土體的非線性破壞特征。

(2) 彌補了Mohr-Coulomb強度準則中巖體不能承受拉應力以及對低應力區不太適用的不足，能解釋低應力區、拉應力區及最小住應力σ3對強度的影響，因而更符合巖土體的破壞特點。

2上限求解

2.1地基單元的劃分

最早在邊坡極限分析中，就擋墻后的破裂體作為一個剛體來進行極限分析的，Daris(1968年)研究了由兩個剛性滑塊組成的破壞機構，而Soubra[4]和Michalowski[5]則嘗試了將地基分成更多塊剛性的滑塊，然后采用線性Mohr-Brown破壞準則，本文亦采用該法，但采用的是非線性Hoek-Brown破壞準則。由于圓形基礎是關于基礎軸對稱的，故可取其一截面作為示意圖，如圖1所示。

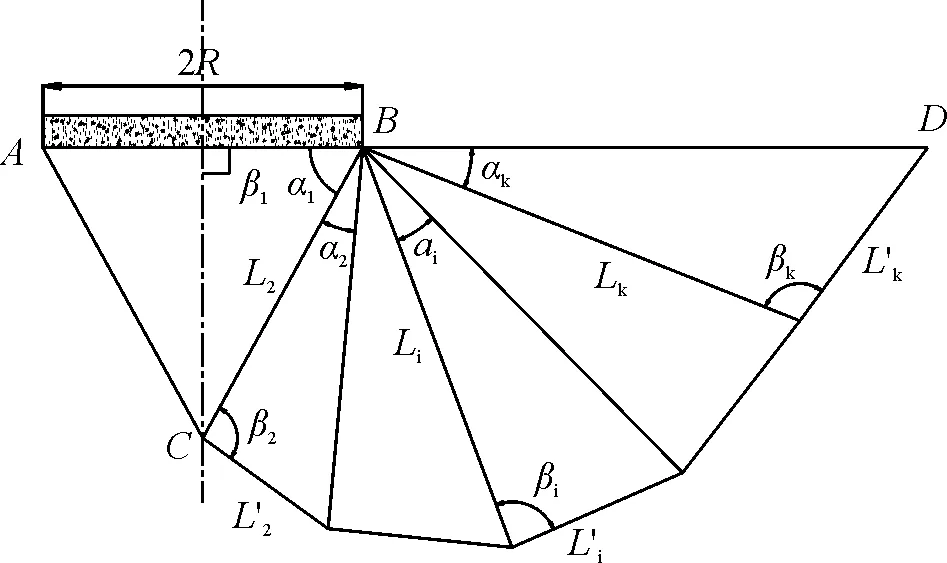
圖1　地基單元劃分截面示意

根據幾何關系可推斷出：

(2)

(3)

假定塑性功的耗散只發生在三角形公共邊和底邊上，每個單元的速度場和速度方向如圖2所示。

圖2　地基單元速度場截面示意

根據個單元相對關系規定：V1為基礎底部1號塊的絕對速度，Vi為地基中第i號塊的絕對速度，V1,2為1號塊和2號塊之間的相對速度，Vi-1,i為第i-1號塊與第i號塊之間的相對速度。根據速度場閉合的原則可得出如下的關系：

(4)

(5)

根據圖1可確定的邊界條件有：

(3)0≤βi≤π(4)0≤φi≤π

2.2荷載功率的計算

選取第i個單元作為分析對象，如圖3所示。

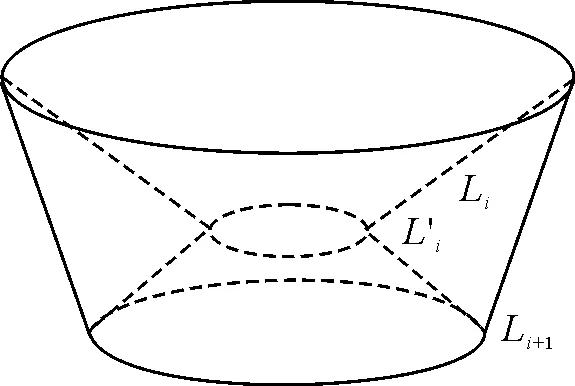
圖3　第i個單元示意

則第i個單元的體積可表示為：

(6)

其中，qi為αi和βi組成的函數。

2.2.1內能耗散功率

由于內能的耗散僅發生在速度不連續面上，即環形三角形單元的公共邊和底邊上，可求得內能耗散率為：

(7)

其中，c和c’分別是三角形單元公共邊和底邊上的瞬時粘聚力。

式(2)～式(5)代入式(7)求得內能耗散率為：

(8)

其中，f1、f2為由αi、βi、φi、φ’i、c和c’組成的函數。

2.2.2重力功率

根據單元的自重可求得重力做功率為：

(9)

式(4)、式(6)代入式(9)可得：

(10)

其中,f3為由αi、βi、φi和φ’i組成的函數。

2.2.3超載功率

設地面的均布荷載為q0，分布的范圍為第k號環形三角形單元的邊長Lk+1，位移方向為第k號環形三角形單元的絕對速度方向，則超載做功率可以寫成：

(11)

式(2)、式(4)代入式(11)可得：

(12)

其中,f4為由αi、βi和φi和φ’i組成的函數。

2.2.4極限荷載功率

據虛功率平衡的原理有：

(13)

式(8)、式(10)、式(12)代入上式可得：

(14)

式(14)即為圓形基礎地基極限承載力的上限解，該式的表達式很復雜，直接計算難度很大。MATLAB(MatrixLaboratory)具備較好的數值計算能力，其中的序列二次規劃法(SQP)優化可用于式(14)的計算。

3計算結果分析

文獻[2]中建立了c與φ的關系式，即：

(15)

式中：m、a、s為由巖土材料參數GSI、mi確定；σc為巖土材料抗壓強度。

文獻[6]根據測定的c、φ計算求得地基承載力的上限解析解，由于c、φ值都是唯一的，即作者計算時將巖土材料默認為是線性的。從本文第2節可以看出，本文將圓形基礎地基劃分為多個單元，每一個單元平移時呈各自不同的值，即φi或φ’i即將巖土材料默認為是非線性的。

為分析比較，將地基分為12個單元，即k=12，其他相關參數取：q0=0、γ=0、D=0、σc=90kPa、R=0.5m、mi=2。通過MATLAB中的SQP優化法計算結果見圖4。

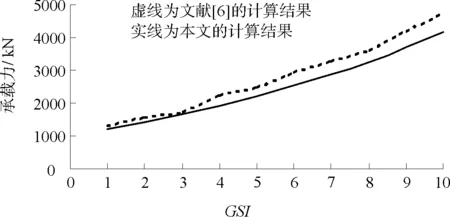
圖4　文獻[6]與本文計算結果比較

從計算結果來看，本文的計算結果明顯小于文獻[6]的計算結果。地基不同部位的應力場是不同的，巖土材料在不同的應力條件下強度指標也是不一樣的，本文采用的計算方法正好反映了這一點，即更能反映巖土非線性的特征。

4結束語

計算結果表明，本文得出的非線性情況下的圓形基礎地基承載力明顯小于線性情況下的結果。地基土破壞時，不僅在地基內形成一連貫的滑移面，而且在滑移體內也有相對的滑移，本文將地基劃分為多個滑動單元，單元之間的相對滑移也能反映滑移體內相對的滑移；本文對每個滑移面采用不同的c、φ值，反映了巖土材料在不同的應力條件下非線性的特征。所以，本文的計算方法更接近于地基破壞時的真實值，該法值得在實際工程中參考。

從程序運行來看，如果單元劃分得太多，程序的計算量將大大增加，計算將難以進行。當單元數目恰當時，隨著劃分單元數目的增加，所求得的圓形基礎地基承載力是逐漸減小的，而且減小的幅度越來越小。可以認為：如果計算能力允許，只要單元劃分足夠多、足夠細，計算結果就能達到真實解。

參考文獻

[1]HockE.Strengthofjointedrockmasses,1983RankineLecture.Geotechnique1983， 33(3)：187-223.

[2]HoekE.EstimatingMohr-CoulombfrictionandcohesionvaluesfromtheHoek-Brownfailurecriterion.IntJRockMechMinSciGeomech1990，27(3):27-32.

[3]巫德斌，徐衛亞.基于Hoek-Brown準則的邊坡開挖巖體力學參數研究[J].河海大學學報，2005，33 (1): 89-93.

[4]SoubraAH.Upper-boundsolutionsforbearingcapacityoffoundations.ASCEJ.Geotech.Geoenviron.Eng1999，125(1):59-68.

[5]MichalowskiRL.Anestimateoftheinfluenceofsoilweightonbearingcapacityusinglimitanalysis.SoilsFoundations1997，37(4):421-428.

[6]李亮，楊小禮.圓形淺基礎地基承載力極限分析的上限解析解[J].鐵道學報,2001,23(1)：94-97.

[作者簡介]陳中流(1981～)，男，碩士，工程師，從事巖土工程勘察設計工作。

【中圖分類號】TU470+.3

【文獻標志碼】A

[定稿日期]2015-07-30