解題思路程序化——有效降低滑塊木板模型的思維難度
蔡署+江華麗
摘 要 本文首先闡述“滑塊—木板”模型其涉及到的物理概念,著重對共速后滑塊和木板的運動情況進行探究,力求思維過程和解題過程程序化,有效降低滑塊木板模型的思維難度
關鍵詞 “滑塊—木板”;模型;程序化;思維難度
中圖分類號 O4 文獻標識碼 A 文章編號 1674-6708(2016)164-0225-02
1 緒論
“滑塊—木板”模型因其涉及到的物理概念和物理規律較多,運動過程變化多端,運動狀態的綜合性和隱蔽性較強,尤其對力學的三大鑰匙動能定理、動量守恒定律和牛頓運動定律[1]能夠全方位的考查,更能反映學生的實際水平,有更好的選拔作用,且對考綱的綜合分析能力更好的體現,因此,該模型試題常常成為高考命題專家每年命題的重點和熱點。例如,2015年全國高考新課標1卷第25題,2015年全國高考新課標Ⅱ卷第25題,2014年全國高考江蘇卷第8題等。
2 案例分析
鑒于其入手難、思維起點高的特點,筆者一直在思考這類題型是否存在簡單程序化的解題思路,能夠有效減低該類題型的思維難度。筆者發現,學生在解決判斷滑塊木板模型問題時,往往是對兩個物體達到共同速度之后的運動情況分析不清或者是分析比較凌亂。如若清楚二者達到共同速度(靜止或速度相同)之后的運動情況,學生的思維難度就自然而然降低,例如,如果二者發生相對滑動則二者之間的摩擦力必然為滑動摩擦力,求解相對簡單;如果二者一起運動,學生很容易想到運用整體法進行求解。
思維過程程序化。首先,該模型中有2個物體存在,通常要用到整體法和隔離法,找出受力利用牛頓第二定律求出加速度,然后利用勻變速運動的規律解決。其次,滑塊和木板達到共同速度(靜止或速度相同)時,特別要注意下列兩方面的問題:滑塊和木板的相對位移出現極大值和極小值;判斷滑塊和木板是否會繼續發生相對滑動[2]。
解題過程程序化。為了降低思維難度,筆者認為可以先假設二者達到共同速度之后不存在相對滑動,這樣就可以直接從整體法的角度入手,多個物體變成單一物體,思維難度降低。求出整體的加速度,求出二者間的“靜摩擦力f”,與二者的最大靜摩擦力進行對比,若“靜摩擦力f”大于fm,則不符合假設,即二者已經發生相對滑動,二者間的作用力為滑動摩擦力;若“靜摩擦力 f”小于fm,則符合假設,即二者不發生相對滑動,二者間的作用力為靜摩擦力[3]。具體的程序化過程,可以分為“四步曲”:
第一步:求整體的加速度a。假設滑塊和木板不再發生相對滑動,利用牛頓第二定律求出整體的加速度a;
第二步:求出此時的“靜摩擦力f”。將滑塊(或木板)從中隔離出來進行受力分析,利用牛頓第二定律求出此時的“靜摩擦力f”;
第三步:最大靜摩擦力fm。求滑塊和木板間的fm;
第四步:對比f、fm判斷:
若f≤fm,假設成立,即二者不會發生相對滑動;若f>fm,假設不成立,即二者會發生相對滑動。
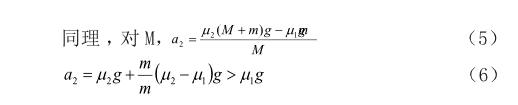
故可知,長木板M先減速到零,接著木塊m再減少到零。
例題2:如圖2所示,滑塊A的質量mA= 1㎏,靜止在光滑水平面上的木板B的質量為mB=0.5㎏,板長L=1m,某時刻A以v0=4m/s的初速度滑上木板B的上表面,為使A不致于從B上滑落,在A滑上B的同時,給B施加一個水平向右的拉力F,若A與B之間的動摩擦因數μ=0.2,取g=10m/s2,試求拉力F大小的取值范圍。
程序化分析:
為使A不致于從B上滑落,則共同速度時,應同時滿足關系: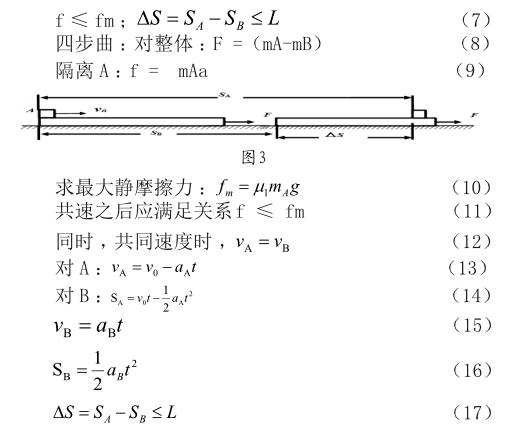
聯立上式,可得:1N≤F≤3N得解。
3 結論
通過以上2道例題分析,可以很清楚的得出:如果采用常規解題過程,即通過假設二者發生相對滑動,求解各自的加速度,無形之中增加了學生思維的難度,若采用程序化的四步曲,以整體法的角度入手,學生的解題思路清晰、步驟簡捷,很好的降低學生思維的難度,碰到共速后滑塊木板的運動問題就能迎刃而解。作為老師如果能在平常訓練中對該方法多加引導,形成了規范的思路過程,對學生解決該類問題定能起到事半功倍的效果。
參考文獻
[1]藍坤彥,向樺,杜娟.高考舊題翻新的方法和技巧初探[J].物理教師,2013,34(5):71-73.
[2]陶漢斌.程序化中的鮮題中的分段與建模[J].數理化解題研究,2014(1):48-49.
[3]林少彬.物理力學“滑塊—木板”模型全攻略[J].理綜高參,2012,(12):61-63.

